改进TOPSIS的多态融合直觉模糊威胁评估

2018-10-15张浩为谢军伟葛佳昂张昭建宗彬锋

系统工程与电子技术 2018年10期

张浩为, 谢军伟, 葛佳昂, 张昭建, 宗彬锋

(1. 空军工程大学防空反导学院, 陕西西安 710051; 2. 空军预警学院, 湖北武汉 410039;3. 中国人民解放军94710部队, 江苏无锡 214000)

0 引言

现代防空作战中,空袭方常采用多层次、多批次、多方向的饱和式攻击手段。作为防空方,对不同批次目标做出合理的威胁评判,对于有效调度力量来组织防空作战,意义重大。

威胁评估的方法众多,典型的如神经网络[1]、证据推理[2]、雷达图[3]等。而在实际作战中,受到传感器性能及环境的限制,所获得的目标数据往往呈现出不完整性、不可靠性等特征。另外,决策者对目标属性的认知也具有模糊性。因此,引入直觉模糊集[4-5],更能刻画评估过程的不确定性本质。并且,基于直觉模糊的多属性决策[6-10]、群决策问题[11-14]正日益成为研究热点。文献[5]从信息融合的角度对现有的直觉模糊集排序方法作了总结。文献[6]基于直觉模糊支持函数、风险函数和可信性函数,构建了直觉模糊的超序关系并将其运用到排序问题中。文献[7]提出了一种基于直觉模糊数、直角三角直觉模糊数和所提出的直觉模糊数的直觉模糊集合平均算子间转换的新的直觉模糊多属性决策模型。文献[8]在决策理论的框架下建立了新的直觉模糊决策模型,其突出了备选方案每个属性之间相互影响而带来的差别。文献[9]提出一种基于正负理想解排序(technique for order preference by similarity to ideal solution, TOPSIS)和直觉模糊数间相似性测度的多属性决策方法。文献[10]提出一种扩展的直觉模糊TOPSIS方法。文献[11-14]研究了群决策中获取一致性的方法,并构建了不同的群决策模型。当前,直觉模糊集广泛用于信用风险[10]、旅店选址[15]、医疗体系[16]等各类评估问题中。基于此,文献[17-19]研究了目标属性权重未知的威胁评估方法,并在决策过程中考虑了决策者的个人偏好。文献[20-21]利用TOPSIS对直觉模糊集进行排序,得出目标的威胁评估结果。文献[22-23]利用直觉模糊熵(intuitionistic fuzzy entropy, IFE)计算属性权重,构建了动态目标威胁评估模型。文献[24-26]研究了IFE的构造方法,并将其用于多属性决策领域。文献[27-31]从信息的角度出发,利用基于直觉模糊集表达的信息量与信息可靠性构建排序函数。虽然上述方法多样,但尚存在如下不足:一是部分文献[17-18,27-31]提出的基于距离的直觉模糊集排序方法,仅考虑了与正理想点的距离,忽略了与负理想点的距离;二是尽管现有的IFE[20-26,30]形式多样,但对于给定的直觉模糊集和它的余集,仅利用IFE难以进行区分;三是大部分文献[17-21,24-31]的评估方法仅针对当前时刻,忽略了之前多个时刻的信息,难以得出综合、可靠的评估结果。鉴于此,本文提出一种基于TOPSIS与IFE的多态融合直觉模糊威胁评估模型。首先,结合目标属性的主、客观权重计算综合权重;其次,通过TOPSIS计算得出的相对贴近度的大小,并以此来表征直觉模糊集的信息量,利用IFE来表现信息的可靠性,引入决策者的风险偏好,以构建基于信息量和信息可靠性的直觉模糊集排序模型。然后,利用偏好集结-源集结-距离计算(distance calculation-source aggregation-preference aggregation, d-s-p)模型集结多名决策者的决策信息,以使得信息得到最大化保留。最后,赋予时间序列权重,融合多个时刻的决策信息,得出最终的威胁排序结果。通过仿真算例及方法对比,验证了本文算法的可靠性和有效性。

1 预备知识

定义1[4]设X为一给定的论域,则称A={|xi∈X}为X上的一个直觉模糊集。其中,μA(xi)∈[0,1],为A的隶属度函数;νA(xi)∈[0,1]为A的非隶属度函数。且满足0≤μA(xi)+νA(xi)≤1。进一步,称πA(xi)=1-μA(xi)-νA(xi)为A的犹豫度。

定义2设Ai=<μi,νi> (i=1,2)为两个直觉模糊集,k为实数且满足k>0。则两者的运算关系:

(1)A1+A2=<μ1+μ2-μ1μ2,ν1ν2>

(2)kA1=<1-(1-μ1)k,ν1k>

(3)A1的余集A1c=<ν1,μ1>

(4)A1⊆A2,当且仅当μ1≤μ2且ν1≥ν2

定义3设Ai=<μi,νi>(i=1,2,…,n)为直觉模糊集的集合,ωi(i=1,2,…,n)为权重序列,则直觉模糊加权平均算子可表示为

(1)

2 综合权重模型

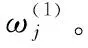
IFE能较客观地反映直觉模糊集的有序性:若某一指标的熵值越小,其不确定性越大,应赋予的权值越大。为准确度量直觉模糊集的模糊程度,文献[24-26]构造了不同形式的IFE,并对其公理化定义进行了探讨。文献[25]指出,IFE应包含两方面信息:不确定程度和未知程度。其中,不确定程度通常用隶属度和非隶属度的绝对偏差来表示,而未知程度应以犹豫度来表征。对此,文献[25]构造了一种结合犹豫度的IFE,以克服以往IFE中仅考虑不确定程度而忽略未知程度的不足。则tk时刻m个目标中第j个属性的IFE可计算为

(2)

此时,目标属性对应的熵权重为

(3)

得到目标属性的主、客观权重后,需对权重进行综合。需对权重进行综合。权重的综合方法,通常有加权法和乘积法等。其中,加权法在综合考虑主客观意图的前提下,通过对主、客观权重分别赋予权值来求取平均权重,但涉及到权值的选择问题。乘积法更加突出权重较小一方的作用,无需计算权值。因此,采用乘积法求取综合权重:

(4)

3 多时刻排序模型

文献[27]从信息的角度出发,指出直觉模糊集包含以下内容:信息量的大小和信息的可靠性程度。基于此,文献[27,31]利用与正理想点的距离来代表信息量的大小,用犹豫度来表征信息可靠性。但其均忽略了与负理想点之间的距离。并且,犹豫度难以完全表现信息的可靠性。目前,TOPSIS广泛运用于直觉模糊集的相似性测度中。在TOPSIS中,若该点距离正理想点越近、距负理想点距离越远,则该点越佳。因此,可以利用TOPSIS来衡量信息量的大小[33]。另外,IFE能较为精准地描述直觉模糊集的模糊程度。因此,结合TOPSIS与IFE,通过引入决策者的风险偏好,提出一种新的直觉模糊集排序模型。

3.1 基于TOPSIS与IFE的排序函数

设tk时刻的直觉模糊评判矩阵F(tk)=(fij(tk))m×n,fij(tk)=<μij(tk),νij(tk)>。其中,i=1,2,…,m为目标集,j=1,2,…,n为属性集。F(tk)中,正理想解序列为每个威胁属性取所有目标中最具威胁解,负理想解为威胁值最小的解。对于效益型指标,正理想解取指标最大值;对于成本型指标,正理想解取指标最小值。反之,可得出负理想解,公式如下:

正理想解为

(5)

负理想解为

(6)

则第i个目标的第j个属性到正、负理想解的欧式距离可表示为

(7)

(8)

tk时刻目标i的第j个属性与正理想解的相对贴近度计算为

(9)

其IFE可表示为

(10)

式(9)表现了信息的确定性,而式(10)表达了信息的未知性。在此,引入决策者的风险偏好,来构造一种新的直觉模糊集排序函数:

(11)

式中,Pij的值越大,属性的威胁度越大。t为风险因子,反映了决策者的风险偏好。当t∈(0,1)时,相比于Dij,决策者更看重Eij可能带来的风险;当t>1时,相比于Eij,决策者更看重Dij带来的确定性威胁;当t=1时,决策者认为两者同等重要。

3.2 基于d-s-p模型的多源信息集结

在多名决策者参与决策的过程中,需要对不同决策者的决策信息进行集结[34]。文献[35]对运用不同模型丢失的信息量进行对比,发现d-s-p模型丢失的信息更少,排序结果更加准确。因此,采用d-s-p模型对不同的源信息进行集结。

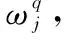
→(Pij)m×n→Pi

设rij=<αij,βij>,fij=<μij,νij>,两者间的关系为

(12)

3.3 时间序列权重

在防空作战中,目标威胁程度的大小会随时间动态变化。要得到全面、综合的威胁评估结果,不仅要利用当前时刻信息,更要兼顾之前多个时刻的信息。因此,选取当前(p时刻)及之前p-1个观测时刻对目标的采样数据进行评估,采用泊松分布逆形式对时间序列赋予权重,则tk时刻的权重值为

(13)

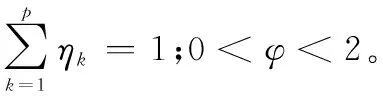
4 算法流程

综上所述,改进TOPSIS的多态直觉模糊威胁评估步骤如下:

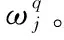
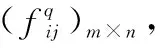
步骤3融合g个决策者的决策信息,得出单时刻目标威胁排序。

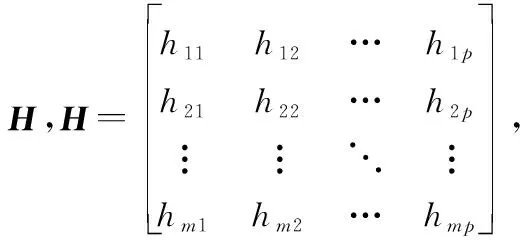
步骤5运用TOPSIS法得到最终的目标威胁排序。

5 仿真算例

假定在某次防空演习中,有5批目标对我方进行空袭,在获得连续3个时刻目标的区间值形式的数据后,将其转化为直接模糊数形式后(关于区间数和直觉模糊数间的相互转换,可参考文献[17-18]),如表1所示。

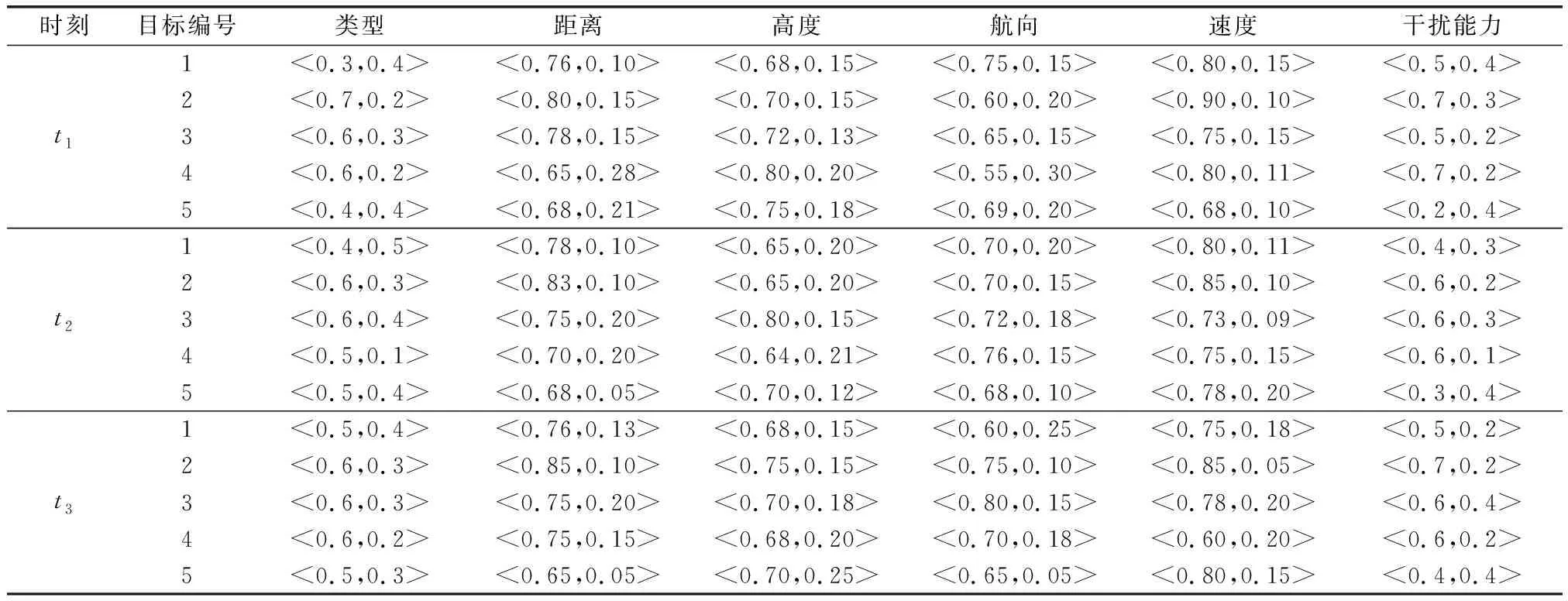
表1 t1～t3时刻的目标信息

根据t1～t3时刻的目标信息,可得不同时刻目标属性的熵权重为

ω(2)(t1)=

[0.064 2,0.217 6,0.213 3,0.131 0,0.302 1,0.071 8]

ω(2)(t2)=

[0.032 9,0.250 2,0.174 8,0.198 2,0.290 3,0.053 6]

ω(2)(t3)=

[0.048 7,0.255 1,0.177 0,0.192 4,0.260 6,0.066 3]

若决策过程中有4名决策者参与决策,其权威性分别为:λ=[0.247 1,0.232 4,0.250 0,0.270 6];决策者1～4给出的目标属性的主观权重分别为

ω1=[0.28,0.23,0.12,0.10,0.17,0.10]

ω2=[0.40,0.25,0.10,0.05,0.15,0.05]

ω3=[0.20,0.28,0.12,0.15,0.17,0.08]

ω4=[0.20,0.30,0.15,0.10,0.15,0.10]

根据综合权重模型,可以得到4位决策者对于目标属性在t1～t3时刻的综合权重分别为

ω1(t1)=

[0.108 8,0.302 8,0.154 9,0.079 3,0.310 8,0.043 5]

ω2(t1)=

[0.163 7,0.346 8,0.136 0,0.041 8,0.288 9,0.022 9]

ω3(t1)=

[0.072 9,0.345 9,0.145 3,0.111 6,0.291 6,0.032 6]

ω4(t1)=

[0.073 1,0.371 5,0.182 1,0.074 5,0.257 9,0.040 9]

ω1(t2)=

[0.056 7,0.354 7,0.129 3,0.122 1,0.304 2,0.033 0]

ω2(t2)=

[0.088 0,0.419 0,0.117 1,0.066 4,0.291 7,0.018 0]

ω3(t2)=

[0.036 3,0.387 1,0.115 9,0.164 2,0.272 7,0.023 7]

ω4(t2)=

[0.037 2,0.425 1,0.148 5,0.112 2,0.246 6,0.030 4]

ω1(t3)=

[0.083 3,0.358 4,0.129 8,0.117 5,0.270 6,0.040 5]

ω2(t3)=

[0.127 3,0.416 9,0.115 7,0.062 9,0.255 5,0.021 7]

ω3(t3)=

[0.053 8,0.394 9,0.117 4,0.159 5,0.244 9,0.029 3]

ω4(t3)=

[0.054 8,0.430 5,0.149 4,0.108 2,0.219 9,0.037 3]

若4位决策者的风险因子均为2,则4名决策者对目标属性的排序函数值为

P1(t1)=

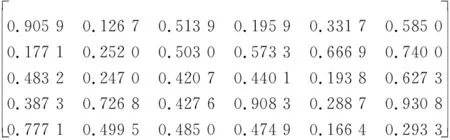
P2(t1)=

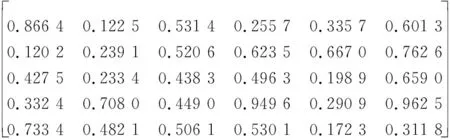
P3(t1)=

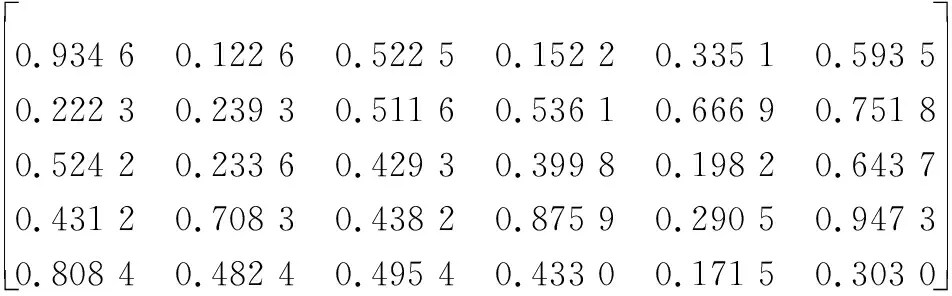
P4(t1)=

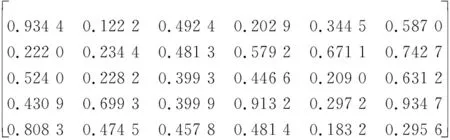
P1(t2)=

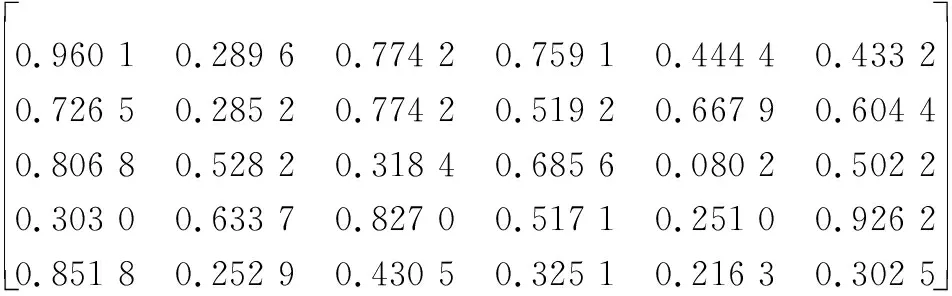
P2(t2)=

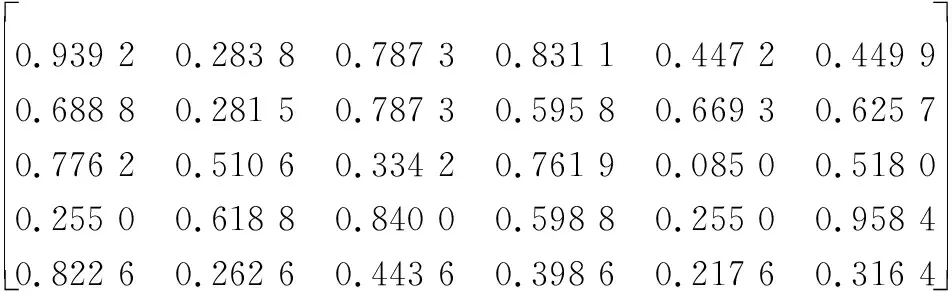
P3(t2)=

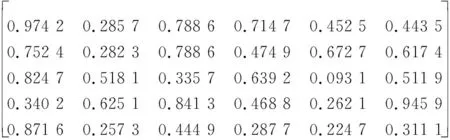
P4(t2)=

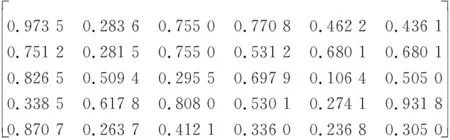
P1(t3)=

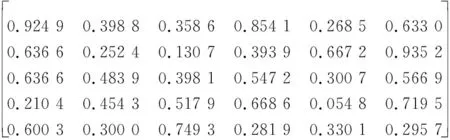
P2(t3)=

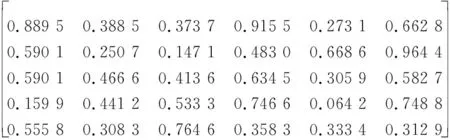
P3(t3)=

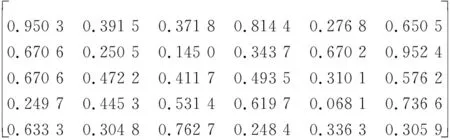
P4(t3)=

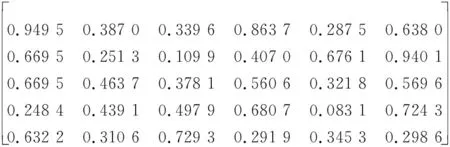
融合4名决策者的决策信息,得出t1～t3时刻的目标威胁分别为

P(t1)=[0.446 4,0.487 7,0.405 5,0.613 6,0.451 0]T

P(t2)=[0.614 0,0.600 8,0.490 4,0.581 9,0.402 4]T

P(t3)=[0.577 5,0.508 5,0.492 6,0.443 4,0.432 9]T

时间序列权重中,取φ=1.5,则ηk=[0.200 0, 0.266 7,0.533 3]。构造加权多时刻融合决策矩阵

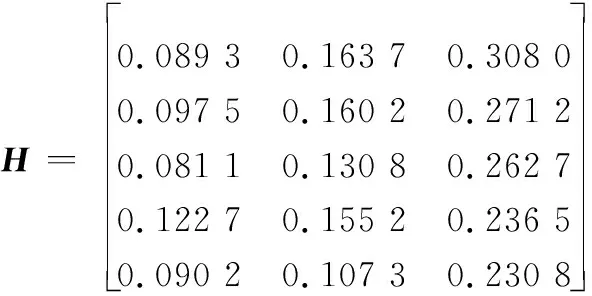
利用TOPSIS法求得目标最终威胁为

P=[1.000 0,0.816 0,0.488 2,0.633 0,0.111 5]T

则目标最终威胁排序为:目标1>目标2>目标4>目标3>目标5。若单纯利用t3时刻的目标信息,得出的威胁排序为:目标1>目标2>目标3>目标4>目标5。从单时刻目标威胁的排序结果可以看出,t1和t2时刻目标4的威胁度均高于目标3,而t3时刻目标4的威胁度稍低于目标3,因此融合多时刻的评估结果更加合理。

将本文方法与文献[22]方法进行对比,文献[22]最终的威胁评估结果为:P=[1.000 0,0.926 0,0.486 3,0.641 9,0.067 2]T,目标最终威胁排序为目标1>目标2>目标4>目标3>目标5,与本文方法一致,验证了本文方法的正确性。但本文方法中,不同决策者可以根据自己的风险偏好选择风险因子,具备一定的灵活性。若改变4名决策者的风险因子t(为简单起见,在此认为4位决策者风险因子相同),则最终目标威胁排序如表2所示。

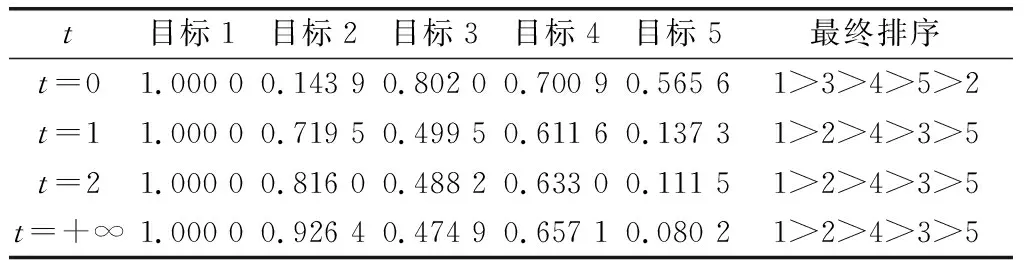
表2 决策者的风险因子与排序结果

由表2可以看出,当t=+∞时,5批目标的威胁计算结果与文献[22]的结果相差很小。这是由于当t>1时,决策者更加看重直觉模糊集所表现得信息量的多少,即由TOPSIS计算的相对贴近度。当t=+∞,本文方法退化为以TOPSIS为主的方法,与文献[22]方法相似。而当t<1时,决策者更加看重直觉模糊集所表现的信息的可靠性,即IFE的计算结果,故此时本文方法的威胁排序结果与文献[22]方法有较大出入。但相比于文献[22]方法,本文具有以下优势:一是考虑了多名决策者对目标属性权重的主观意图,将主、客观权重合成得到综合权重。文献[22]算法仅利用直觉模糊熵得到客观权重,忽略了多名决策者的主观意图。二是构建了新的直觉模糊集排序模型。根据TOPSIS中的相对贴近度来表征直觉模糊集信息量的大小,利用直觉模糊熵来衡量直觉模糊集信息的可靠性,通过决策者的风险偏好模型,定义了新的排序函数。而文献[22]仅利用了TOPSIS中的相对贴近度,忽略了信息的可靠性。三是本文算法可以根据决策者的风险因子进行调整,更具灵活性。而文献[22]没有考虑决策者的风险态度,得出评估结果较为单一。

文献[36]提出一种考虑决策者风险偏好得分函数,若采用文献[36]的方法,则最终的威胁评估结果与目标最终威胁排序如表3所示。其中,ρ为文献[36]中的风险因子,ρ∈[-1,0)时,决策者厌恶风险;ρ∈(0,1]时,决策者偏好风险;ρ=0时,决策者为风险中立者(为简便期间,在此同样认为4位决策者的风险因子相同)。

表3 采用文献[36]方法的决策者风险因子与排序结果

从表3中可以看出,最终的威胁排序结果随着决策者风险因子的不同发生变化,基本可以体现出决策者风险偏好对最终评估结果的影响,也证明了本文方法中考虑决策者风险因子的合理性。但相比于文献[36]的方法,本文方法具有以下优势:一是文献[36]中的得分函数构建缺乏理论依据,而本文的排序函数建立在文献[27]的严格推导的基础上,具有理论支持。并且,文献[28,33]均已指出,相比于采用距离或熵值构建的排序函数,得分函数更易得到许多与直觉相悖的结果。二是文献[36]中的排序函数仅利用了t3时刻的目标信息,得出的结果有失偏颇。而本文方法通过赋予时间序列权重,将t1～t3时刻的目标信息进行综合后得出威胁评估结果,更加合理、可靠。三是从最终的数值计算结果来看(对比表2和表3),文献[36]的方法得出的威胁评估值较为接近,不易区分;而本文方法所得的威胁评估值区分较为明显。