对失控翻滚目标逼近的增广比例导引律控制
2018-10-15刘将辉李海阳
刘将辉, 李海阳
(国防科技大学空天科学学院, 湖南 长沙 410073)
0 引 言
航天器由于控制系统失效或燃料耗尽等原因导致在空间自由翻滚,对在轨航天器和地面人员的安全造成严重威胁[1]。2009年2月10日,美国铱星公司的Iridium-33卫星和俄罗斯失效的通信卫星在西伯利亚上空790 km处发生碰撞而坠毁。2011年9月24日,美国一颗名为“高层大气研究卫星”(UARS)由于燃料耗尽在失控情况下坠落地面。如能对失效航天器进行在轨修复、燃料加注等操作,将会避免此类事故,从而延长其寿命[2-4]。面向失控翻滚目标的逼近是实施上述任务的基础。
当前,对失控翻滚目标逼近问题,国内外学者进行了大量的研究。文献[5-6]采用θ-D非线性最优控制方法设计闭环回路控制器,该控制器综合考虑了追踪器和目标器之间的相对位姿跟踪及追踪器的帆板挠性运动,通过摄动法求Hamilton Jacobi Bellman方程的近似解,求解过程涉及大量数值运算,所得的控制器是一个无穷级数。文献[7]针对失控翻滚目标的逼近问题,建立了追踪器的参考轨迹和参考姿态模型,设计了六自由度控制的自适应滑膜控制器。文献[8-10]设计了六自由度姿轨一体化滑膜自适应控制器,为确保输出可控,引入了追踪器的饱和幅值。文献[11]针对空间翻滚目标的相对位姿测量问题,提出了一种基于视觉SLAM的相对位姿估计方法。考虑到航天器逼近的不同约束和采样频率,文献[12]设计了可重构约束的动态模型预测控制器。文献[13]采用特征模型的控制方法,设计了相对位置和姿态同步控制器,搭建了系统仿真平台并进行动力学仿真。文献[14]设计了二阶非奇异终端滑膜控制器,改善了系统不确定性及消除了滑膜控制的抖颤性。
一些学者对传动相对动力学模型进行改进,提出了基于视线坐标系的轨道动力学模型[15],基于视线制导,文献[16]定性分析了重力差项,给出了一种开关控制算法。
视线坐标系下的比例导引律(proportional navigation, PN)是经典的两点速度导引法,广泛用于导弹拦截领域,具有对目标需求信息较少、易于实现且鲁棒性强等优点[17]。按照控制加速度的施加方向,比例导引律可以分为真比例导引律(true proportional navigation, TPN)和纯比例导引律(pure proportional navigation, PPN)及其对应的变形形式[18],前者控制加速度方向以视线方向为参考,后者以追踪器的速度方向为参考。真比例导引律的控制加速度垂直于视线方向,在视线方向不施加控制。文献[19]提出了自适应的比例导引律用于航空器的近距离操作任务。文献[20]提出了基于滑模控制的纯比例导引律,用于无人追踪航空器和合作航空器的交会。文献[21-23]在视线坐标系的基础上,提出了视线旋转坐标系和视线瞬时旋转平面的概念,将三维空间的相对运动降低到视线瞬时旋转平面内的二维空间运动。文献[24]提出了一种基于零控脱靶量(zero effort miss, ZEM)的增广比例导引律(augmented proportional navigation, APN),用于小行星的着陆任务。
然而,当前的研究主要强调姿轨耦合控制,大多数文献假设的姿态运动过于理想化。对于失控翻滚目标而言,其姿态运动与其质量分布有关,而实际失效航天器的3个惯量主轴是各不相等的,姿态运动也较复杂。姿态与轨道控制解耦,只要知道了其姿态运动特性,对失控翻滚目标的逼近控制则更简单易行。
基于上述研究,本文针对失控翻滚目标的逼近控制问题,在TPN基础上,引入了逼近点视线方向的控制,设计了可用于对失控翻滚目标近距离逼近控制的增广比例导引律控制器。首先,在追踪器视线旋转坐标系上建立了针对任意轨道形式三维相对运动方程。其次,分析了失控翻滚目标在空间中的姿态运动特性,采用了基于反馈线性化的增广比例导引律对追踪航天器进行控制。最后,通过仿真分析验证了所设计的增广比例导引律控制器的正确性和良好的逼近控制性能。
1 相对运动动力学方程
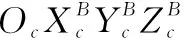
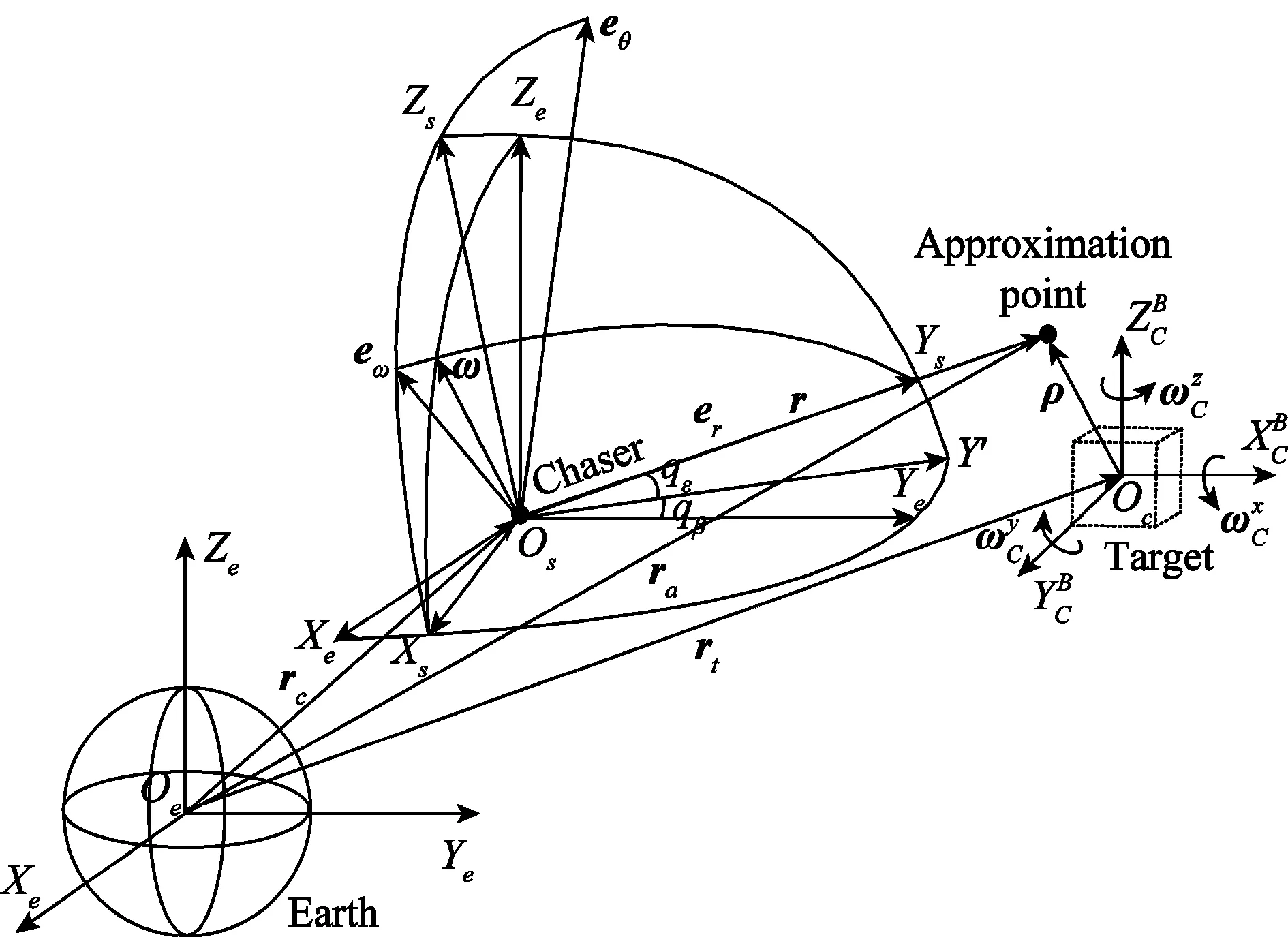
图1 相对运动坐标系统Fig.1 Relative motion coordinate system
为了对翻滚目标实施有效逼近,本文引入了逼近点的概念,逼近点即目标体坐标系中的固定的某点,目标在空间翻滚的过程中,逼近点随着目标的翻滚而一起运动。设逼近点在目标器体坐标系中的位置为ρ,如图1所示。追踪器在J2000中的位置矢量为rc,目标器在J2000中的位置矢量为rt。逼近点在J2000中的位置矢量为ra,速度矢量为νa,有
ra=rt+ρ
(1)
(2)
式中,ωI为目标器体坐标系相对于惯性系翻滚时的角速度矢量。则追踪器相对于逼近点的位置矢量r为
r=ra-rc
(3)
视线方向单位矢量er为
(4)
式中,r是追踪器和逼近点的相对距离;eω为视线角速度方向的单位矢量,eθ=eω×er,er、eθ和eω构成视线旋转坐标系;qε为高低角;qβ为方位角。在视线旋转坐标系下建立三维相对运动方程[23]
(5)
er和eθ组成视线瞬时旋转平面(instantaneous rotation plane of LOS, IRPL);Ωs为eω(IRPL绕er)的旋转角速度;Ωs=Ωser;eω为IRPL的法向;ωs为视线转率,ωs=ωseω。
对式(3)求导,可得追踪器和逼近点的相对速度矢量
v=va-vc
(6)
联立式(3)和式(4),则式(6)变为
(7)
追踪器和逼近点的相对加速度可以由式(6)推导得到
(8)
将式(5)代入式(8),相对加速度表达式转换为
(9)
式(9)可以改写为如下的3个标量子方程
(10)
式中,aa和ac分别代表逼近点和追踪器的加速度;“r、θ和ω”分别代表控制加速度矢量沿“er、eθ和eω”3个方向的分量;Δf为外界干扰加速度。前两式代表IRPL内的相对运动,第三式代表IRPL的转动。相对运动可以分解为IRPL内的相对运动和IRPL的转动。
2 失控翻滚目标的姿态运动特性
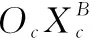
以目标航天器的本体坐标系为计算坐标系,则由矢量相对导数公式可得[25]:
(11)
式中,ω为目标航天器的角速度;L为外力矩;H=I·ω,I为惯量张量。式(11)写成分量的形式为
(12)
设三体轴为惯量主轴,当L=0时,航天器作无外力矩定点转动,得到无外力矩的欧拉动力学方程:
(13)
根据动量矩守恒有
(14)
根据动能守恒有
(15)
将式(14)和式(15)合并可得
(16)
按313的顺序旋转得到进动角φ、章动角θ和自转角φ,则角速度ω可表示为
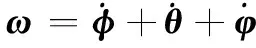
(17)
表示分量的形式为
(18)
(19)
(20)
将航天器角动量H投影到主轴坐标系OsXIYIZI中可得:
Ixωx=Hsinθsinφ
(21)
Iyωy=Hsinθcosφ
(22)
Izωz=Hcosθ
(23)
(24)
(25)
(26)
(27)
(28)
(29)
航天器在空间转动的形式取决于航天器的质量分布。质量分布不对称的失控航天器在空间中作欧拉-班索运动。
3 APN设计
本文在传统的TPN的基础上加入基于反馈线性化的视线方向控制,得到APN。
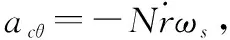
(30)
式中,N为导航比。
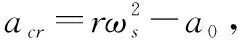
(31)
式中,a0是acr的常数项。需要说明的是,式(31)适用于视线方向目标机动过载不大的情况。如果视线方向的机动过载很大,则不再适用。对式(31)求解得
(32)
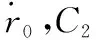
(33)
对方程(33)求解,可得追踪器对逼近点的接近时间:
(34)
追踪器对逼近点的接近速度
(35)
将式(32)和式(35)代入式(30)可得
(36)
式(36)可以转换为如下形式:
(37)
积分式(37),可得ωs:
(38)
由式(38)可以得出,当追踪器接近逼近点时,为保证追踪器相对逼近点的视线转率收敛,N需满足N>2。追踪器控制加速度大小为
(39)
4 仿真分析
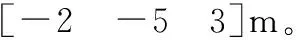
仿真结果如图2~图9所示。图2为失控翻滚目标体坐标系的角速度变化曲线,角速度呈周期性变化,Z方向的角速度变化较小,其余两方向的角速度变化较大。
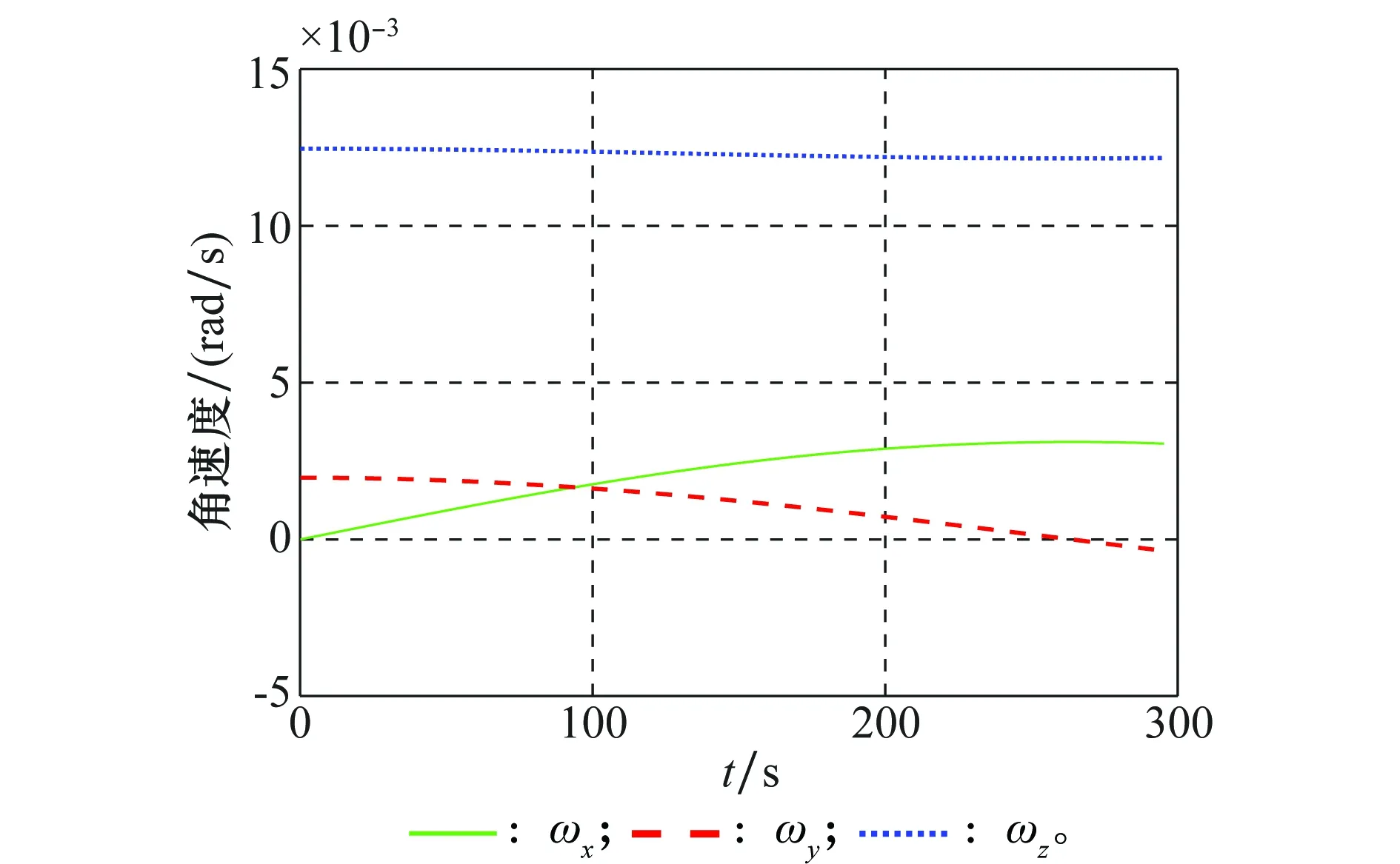
图2 角速度随时间变化Fig.2 Angular velocity versus time
图3是追踪器相对于逼近点的三维相对运动轨迹,将惯性系平移到逼近点,作为参考系。由于目标器在空间中做自由翻滚运动,故追踪器的最后逼近段轨迹不同于交会对接中常见的准直线型的三维相对轨迹。追踪器先绕到目标器体坐标系的某一特定位置,然后对逼近点进行缓慢的接近,保证了逼近过程的安全性。图4是逼近过程中追踪器和逼近点相对距离随时间的变化规律。追踪器逐渐接近逼近点,两者相对距离逐渐减小到零,总的消耗时间为295 s。
图5为IRPL转率曲线,图6为视线转率曲线。整个逼近过程中,IRPL转率极小,近似于0。视线转率从初始的0.038 8 rad/s,逐渐减到0.000 5 rad/s,之后在这个值范围内保持稳定,末端时刻,略微增大了。
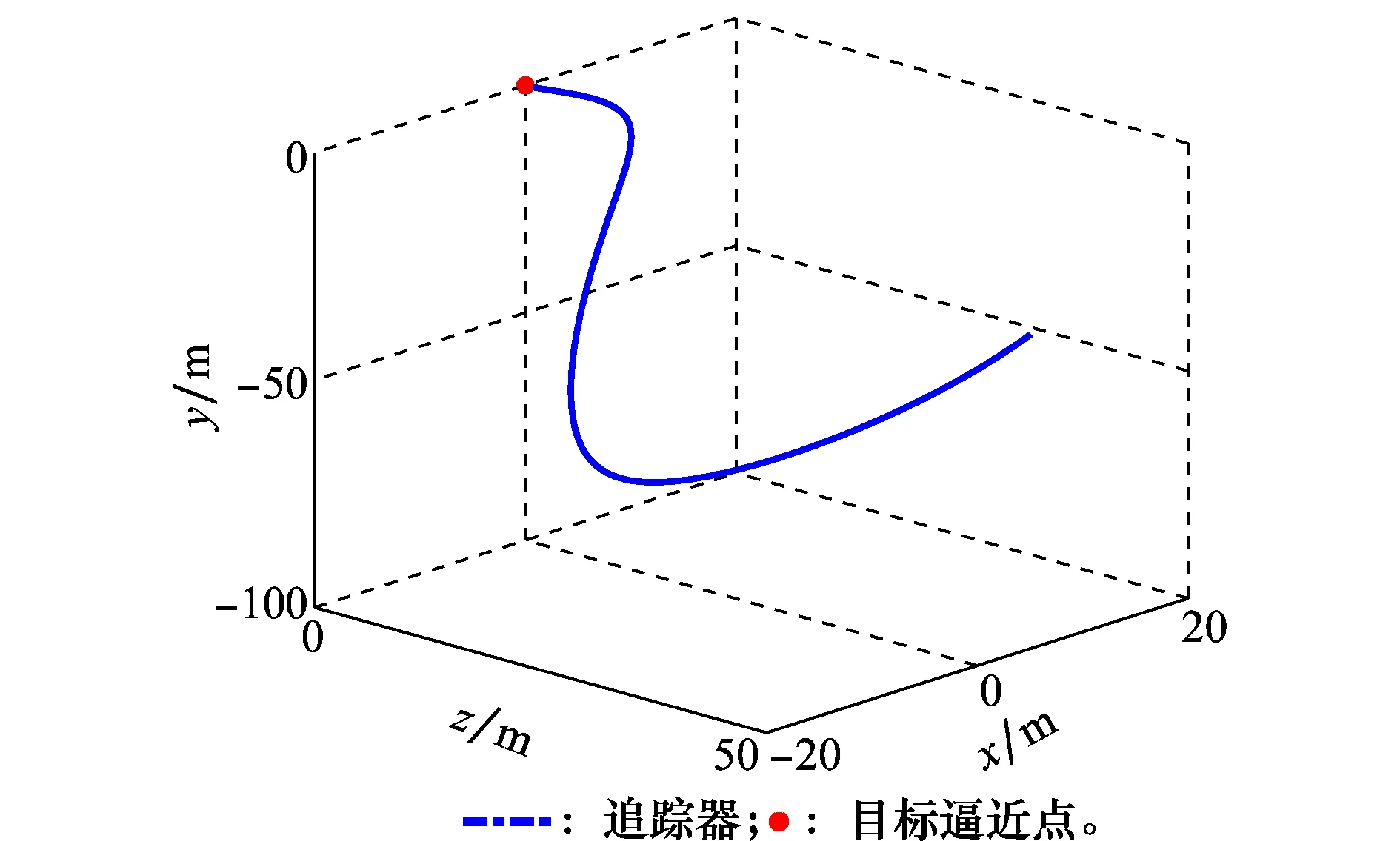
图3 追踪器相对于逼近点的三维相对运动轨迹Fig.3 Three dimensional trajectory of the chaser relative to the approximation point
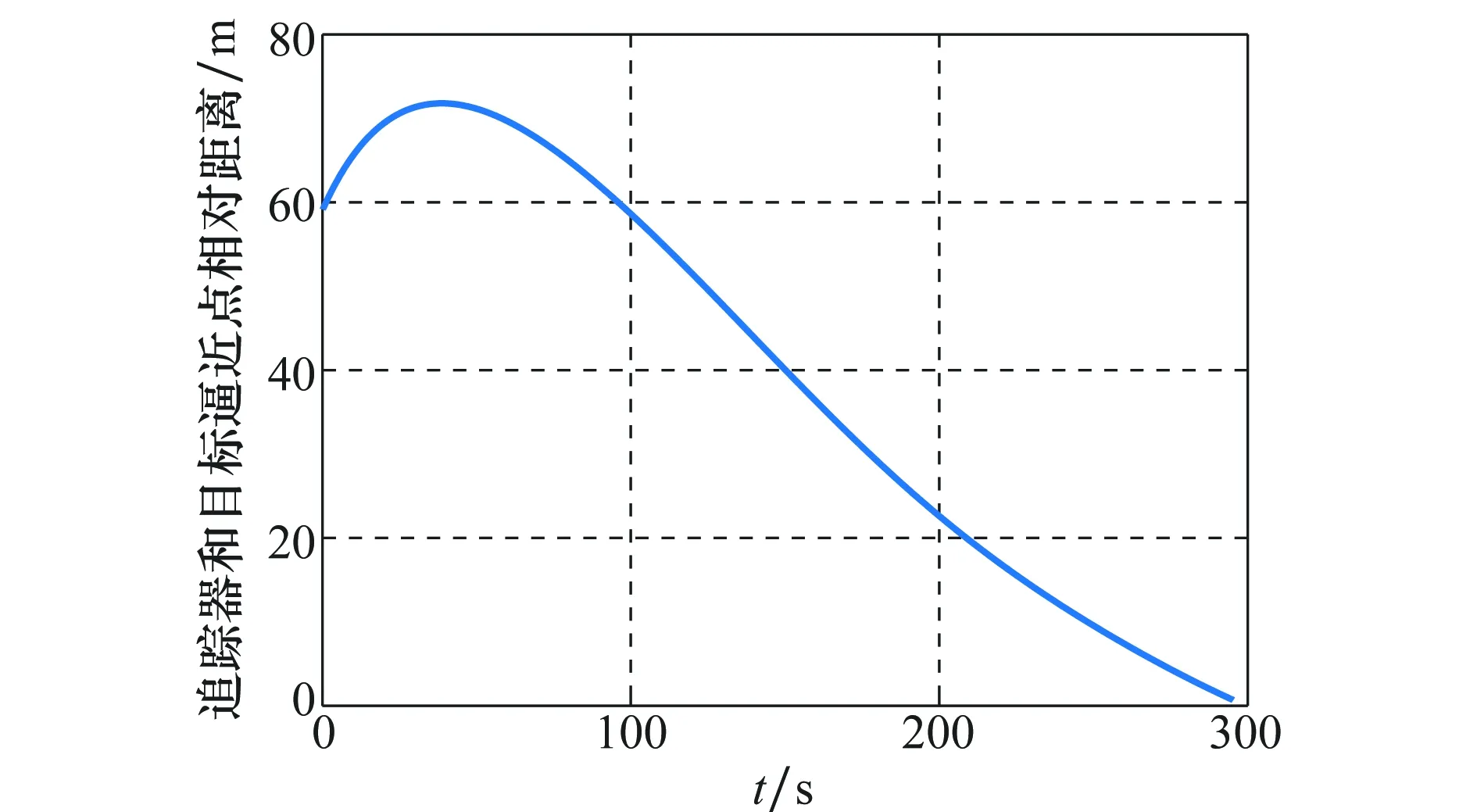
图4 追踪器和逼近点的相对距离Fig.4 Relative distance between the chaser and the approximation point
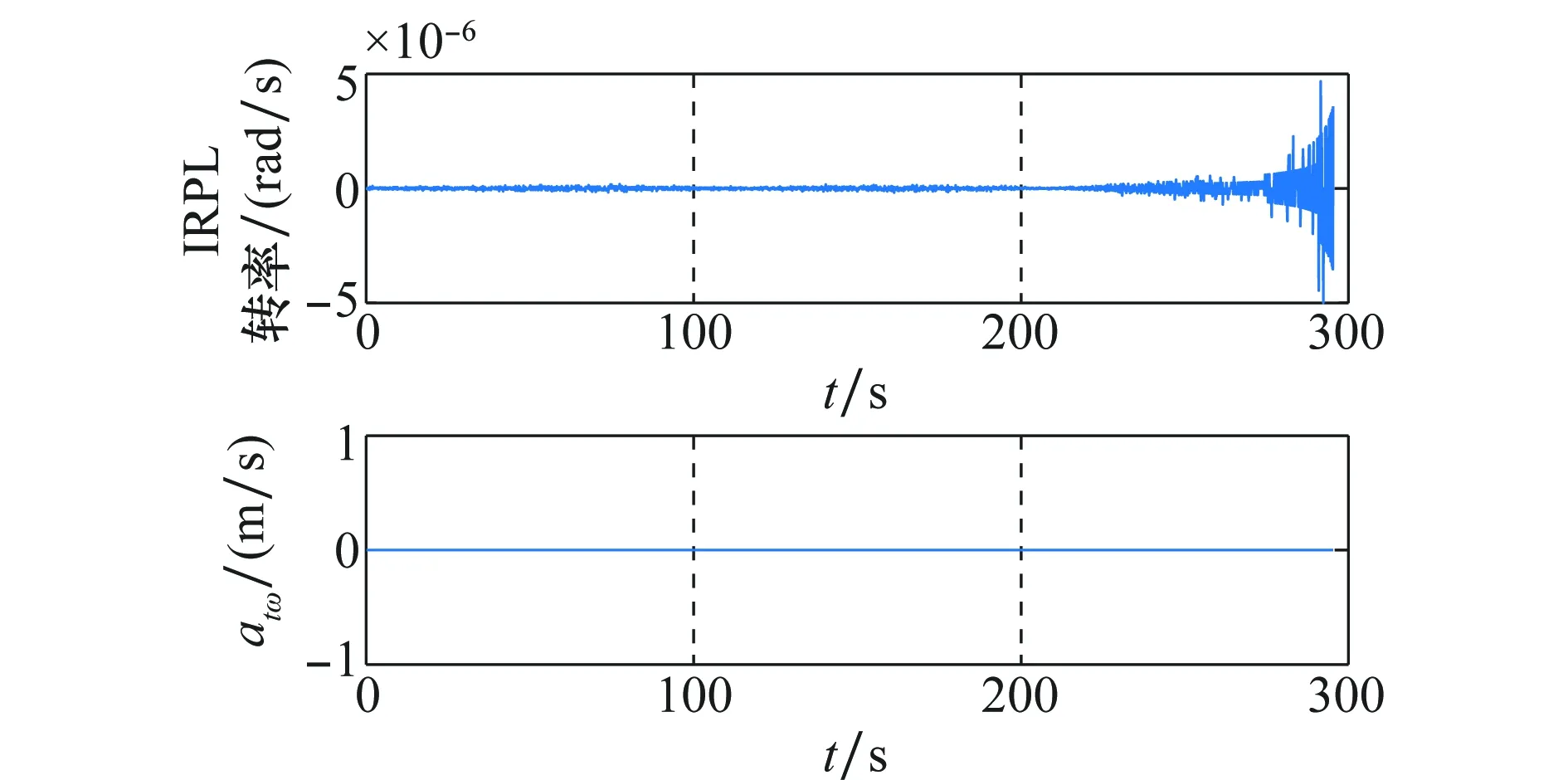
图5 IRPL转率曲线Fig.5 Transfer rate curve of IRPL
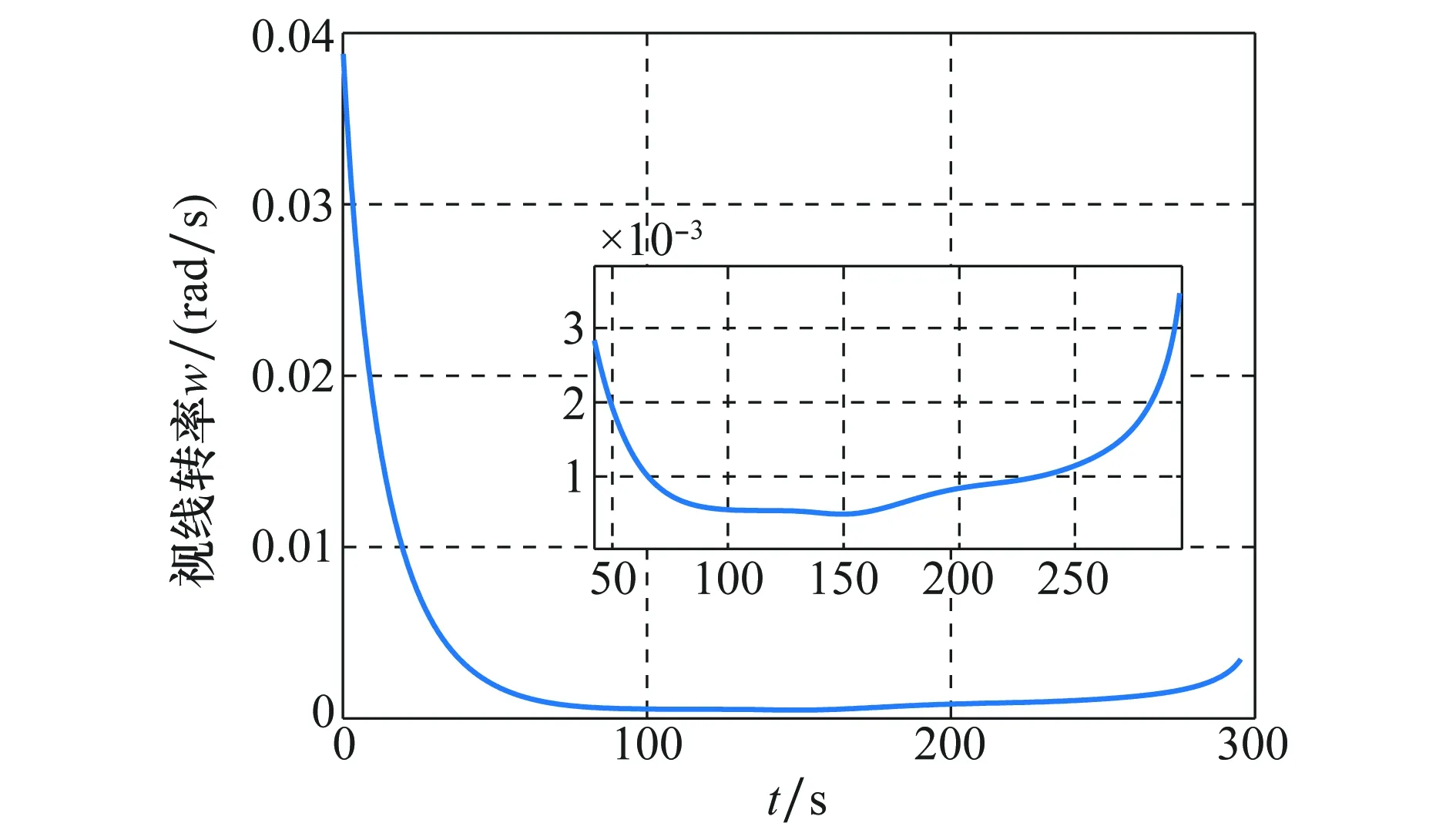
图6 视线转率曲线Fig.6 Transfer rate curve of line of sight
图7为IRPL内追踪器与逼近点间相对速度的变化曲线,垂直逼近点视线方向的速度呈减小的趋势,最后趋向于零。沿逼近点视线方向的速度先减小,然后略微增大,最后稳定在一个极小的值,约为0.32 m/s。图8为IRPL面内视线方向和垂直视线方向的控制加速度变化曲线,控制加速度逐渐减小。视线方向控制加速度由初始的0.128,逐渐减小,稳定在0.000 04 m/s2附近。垂直视线方向的控制加速度由初始的0.132 m/s2,逐渐减小,最后稳定在0.002 m/s2附近,终端时刻,略微增大,最大为0.011 8 m/s2。图9为总的控制加速度变化曲线,控制加速度逐渐减小,由初始的0.184 m/s2,逐渐减小,最后稳定在一个极小的值0.002 m/s2附近,终端时刻,略微增大,最大为0.011 8 m/s2,消耗燃料极少。
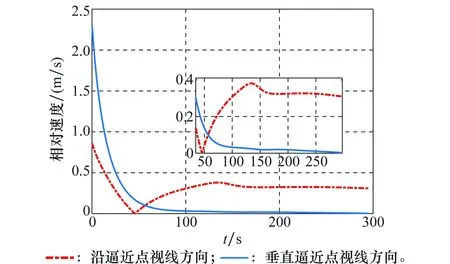
图7 追踪器与逼近点的相对速度变化Fig.7 Relative velocity change of the tracker and the approximation point
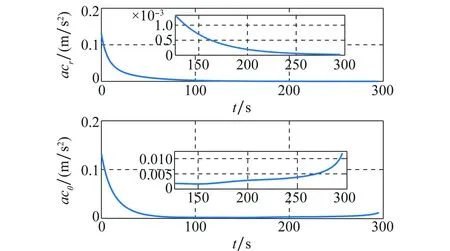
图8 IRPL平面内控制加速度分量Fig.8 Control of acceleration components in IRPL plane
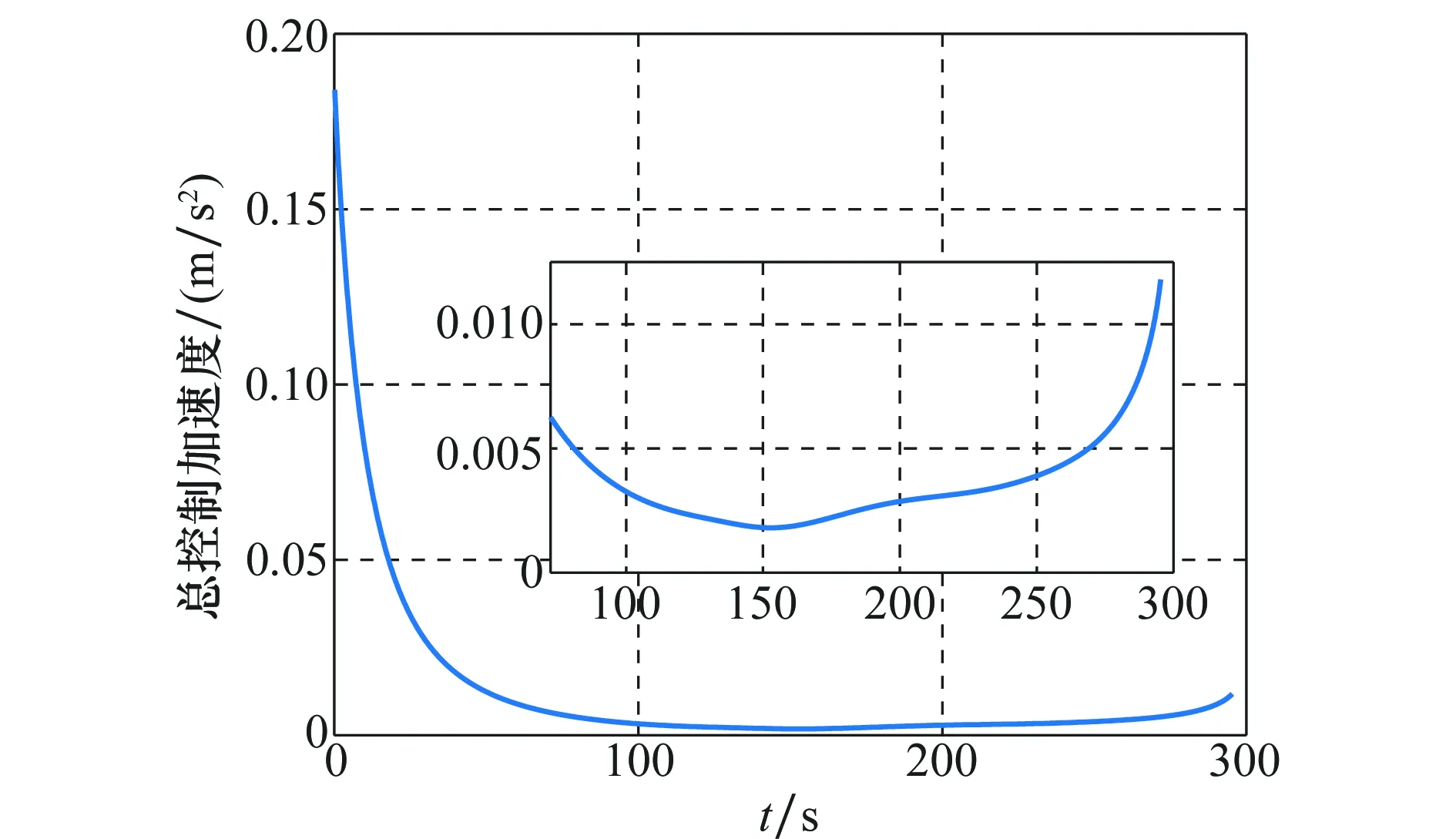
图9 总的控制加速度曲线Fig.9 Total control acceleration curve
5 结 论
本文针对自由翻滚失效航天器的逼近问题,建立了追踪器视线坐标系下追踪器与逼近点的相对运动方程,分析了失控翻滚目标的姿态运动模型,采用了基于反馈线性化的增广比例导引律对追踪航天器进行控制。通过仿真分析得出如下结论:
(1) 通过引入视线方向的控制,基于反馈线性化的增广比例导引律,实现了对失效翻滚目标的有效逼近。实施逼近任务所消耗的燃料较少、逼近时间合理、精度高。
(2) 本文所设计的控制律可实现对翻滚目标任意位置的逼近,具有良好的实用性和工程应用价值。
