考虑节点过载的复杂网络级联失效模型

2018-10-15郝羽成李成兵

系统工程与电子技术 2018年10期

郝羽成, 李成兵, 魏磊

(1. 北京交通大学交通运输学院, 北京 100044; 2. 内蒙古大学交通学院, 内蒙古呼和浩特 010070;3. 北京航空航天大学交通科学与工程学院, 北京 100191)

0 引言

随着网络的规模化、复杂化,微小故障均可能会对网络的抗毁性产生严重影响。由于网络中某节点失效,造成负载重新分配使得其他节点相继失效,如此循环易造成网络大规模瘫痪。在交通网络[1-2]、电力网络[3-5]、通信网络[6]、指挥控制网络[7-8]、供水网络[9-10]方面,级联失效现象已引起学者们的关注。但是,现实中节点通常存在些许冗余能力,并非负载超过其容量就必定失效,这种情况即为节点的过载状态。因此,如何在级联失效过程中减少过载节点数并缓解其承担的负载量以增强抗毁性,将成为网络动力学中研究的重要问题。

在级联失效模型方面,文献[11]最早提出负载容量级联失效模型,根据节点度为负载赋值并进行仿真。文献[12]提出非线性容量负载模型,从网络费用以及鲁棒性两方面对多种网络模型进行研究。文献[13]分别对小世界网络与无标度网络的级联失效现象进行研究,发现两种网络在不同情况下所呈现的抗毁性相反。在加权网络模型方面,文献[14-15]分别以节点度、介数为依据进行加权,结果表明参数在特定值下网络抵抗级联失效的鲁棒性最强。文献[16]基于介数、节点度提出了一种连边加权模型,发现特定参数组合可以增强网络的鲁棒性。文献[17]根据节点与相邻节点的权重提出了一种级联失效模型。在失效节点的负载分配范围方面,文献[18]提出了一种负载局域分配策略的级联失效模型,发现无标度网络构建的参数与鲁棒性相关。文献[19-20]根据负载局域、全局分配策略进行了级联失效仿真。在级联失效优化方面,文献[21-22]分别从容量及其参数两方面对级联抗毁性进行优化。文献[23]以进化算法对复杂网络进行演化,发现聚类系数、模块化、路径距离对于抵抗级联失效现象存在显著影响。在相依网络方面,文献[24-26]分别对小世界网络模型与无标度网络模型进行了级联失效仿真。

综上所述,既有文献大多未考虑节点的过载状态,失效均为确定性的模式,且缺乏对过载节点负载疏散的探讨。然而在现实系统中个体均具有一定弹性。譬如,在交通网络中交叉口的负载大于容量时,交叉口并非完全堵死,只是其运行效率降低,负载的持续增加使其更易失效。基于此,本文考虑过载状态并进行研究,以过载系数描述节点对于负载的冗余能力,以失效概率描述失效的不确定性,以使级联失效模型更贴近于实际网络中失效的情况,从而研究结果具有着较强的实用价值。此外,这有助于拓展级联失效研究的思路,对于网络抵御级联失效、增强抗毁性均存在着重要的理论以及现实意义。

1 考虑节点过载状态的级联失效模型

在既有的级联失效模型中,初始阶段所有节点的负载均小于其容量,节点处于正常状态;若负载大于其容量,则节点为失效状态。在此,考虑节点对于负载的冗余能力,即为节点的过载状态。即使负载大于容量,节点也并非会一定失效,只是运行效率降低并且存在着一定的失效风险。基于此,对级联失效模型进行如下改进:

步骤1假设网络中节点i的容量与负载成正比,则容量ci计算如下：

ci=(1+αi)li

(1)

式中,αi为第i个节点的容忍系数,且αi>0。li为节点i的负载,li计算如下：

(2)

式中,di为节点i的节点度；β为调节负载的参数。

步骤2对节点i进行蓄意攻击,即每次选择负载最大的节点进行攻击。

步骤3失效节点负载分配过程。将失效节点i的负载li以节点度策略分配至相连节点j,并且更新相连节点j的负载。

步骤4过载状态及失效状态判断过程。以过载系数δ描述节点i对于额外负载的处理能力,则其可承受的最大负载为δci。当负载li大于δci时,节点必然失效;当负载li大于ci且小于δci时,节点以一定的概率失效。因此,节点的过载系数越大,网络抗毁性在一定程度上就越强。通过以上分析可知,节点可承受的最大负载需大于其容量,则δ>1。根据式(3)判断相连节点j的状态。

(3)

式中,rand为0至1的随机数；pj为节点j的失效概率。由于在实际情况中,节点对于额外的负载存在着不同的处理能力。部分情况下,节点对于小范围的过载较为敏感,失效的概率增长较快;除此之外也存在着节点对于小范围过载,失效概率增长缓慢的情况。因此,运用分布系数ω对该特性进行刻画,即通过ω调节失效概率pj的分布。其中,pj计算如下:

(4)

通常情况下,负载超出容量的值越大,节点越易失效。因此,pj应是单调递增的函数,则ω>0。

步骤5过载节点负载分配过程。由于过载节点需及时对负载进行疏散,因此以剩余系数λ描述分配负载后节点自身所承担的负载量。当剩余系数λ=0时,过载节点j将当前所有负载进行分配;当剩余系数λ=1,过载节点j将多余的负载进行分配,以保证节点恰好处于正常状态,则剩余系数应满足0≤λ≤1。过载节点j分配至相连非失效节点k的分配量Δljk计算如下:

Δljk=(lj-λcj)Πjk

(5)

式中,Πjk为过载节点j对相连非失效节点k的分配比例。

步骤6判断是否存在失效节点,若存在转至步骤3,否则转至步骤7。

步骤7由于节点处于过载状态,其负载已超过容量并非与正常状态相同,在实际情况中则该节点运行效率低下。为了更好表示过载这一状态,运用修正后最大连通子图的相对大小G进行抗毁性评估,计算式为

(6)

式中,N为网络中的节点数;Φ为网络中未失效节点的集合;若节点h为正常状态,则sh=1;若节点h为过载状态,则

步骤8判断攻击节点数是否满足既定要求,若是则级联失效模型结束,否则转至步骤2。

根据以上叙述,可以发现容忍系数越大,节点可承担的负载越多,在一定程度上网络的抗毁性越强。但是在交通、电力等实际网络中,出于成本因素节点的容量难以无限制增加,因此网络的构建成本也需进行考虑。在不同的负载分配机制下,当网络具有相同的抗毁性而能够避免级联失效现象时,容忍系数较小的网络则其构建成本较小。基于此,本文运用平均容忍系数αc对网络的构建成本进行度量。具体步骤如下:

步骤1对于给定的容忍系数增量Δα,令第t次第i个节点的容忍系数αi为增量Δα,其中i=1。

步骤2对于节点i,根据αi以及相连节点j的负载lj计算其容量cj。

步骤3攻击节点i,并进行失效节点负载分配过程、过载状态及失效状态判断过程和过载节点负载分配过程。

步骤4判断是否存在失效节点,若存在则αi=αi+Δα,并返回步骤2;否则转至步骤5。

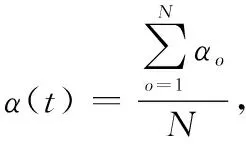
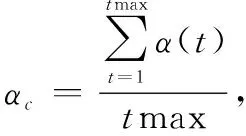
2 过载节点负载分配策略

在级联失效过程中,失效节点负载的分配策略影响着网络的抗毁性。同样,若未及时对过载节点的负载进行疏导,可能使其失效并造成级联失效现象,进而也会影响着网络的抗毁性。因此,本文从以下6个方面对过载节点的负载分配问题进行研究。

(1) 平均分配策略(average distribution,AD)

当过载节点j存在非失效节点k相连时,将负载平均分配至相连非失效节点k。则节点j分配至节点k的分配比例Πjk计算如下:

(7)

式中,m为与过载节点j相连的非失效节点数。

(2) 节点度分配策略(degree distribution,DD)

由于节点度反应了节点所连的边数,因此节点度越大其分配的负载也就越大。则过载节点j分配至相连非失效节点k的分配比例Πjk计算如下:

(8)

式中,Γj为与过载节点j相连非失效节点的集合。

(3) 紧密度分配策略(tightness distribution,TD)

紧密度反应了节点到达其他节点的难易程度,节点的紧密度越大,越易到达其他节点,负载越易疏散。则过载节点j分配至相连非失效节点k的分配比例Πjk计算如下:

(9)

式中,tk表示节点k的紧密度。

(4) 介数分配策略(betweenness distribution,BD)

介数反应了节点在网络中的重要程度,节点的介数越大其重要程度越高。则过载节点j分配至相连非失效节点k的分配比例Πjk计算如下:

(10)

式中,bk表示节点k的介数。

(5) 剩余负载分配策略(surplus load distribution,SLD)

在级联失效过程中,节点的剩余负载越大,其相应可承担的负载也就越多。则过载节点j分配至相连正常节点n的分配比例Πjn计算如下:

(11)

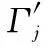
(6) 混合分配策略(mixed distribution,MD)

将以上几种不同的过载分配策略进行加权组合,则可得到混合分配策略。

3 仿真实验

鉴于实际网络均具有着一定的无标度特性[27],因此本文构建Barabasi-Albert(BA)无标度网络模型进行仿真。在BA无标度网络模型中,初始状态是m0个节点的网络,每次迭代引入一个新节点,以节点度计算所得的概率为基础对m(m≤m0)个节点进行连接。本文构建节点数为500的BA无标度网络模型,令m0=5,m=5,若无特殊说明在文中容忍系数αi=1 (i=1,2,…,N),调节负载参数β=2,仿真各自独立运行50次取平均值。分别从过载节点负载分配策略、过载系数、分布系数、剩余系数、平均容忍系数等方面展开对抗毁性的研究。

3.1 过载节点负载分配策略对网络抗毁性的影响

为研究过载分配策略对抗毁性的影响,令过载系数δ=1.5,分布系数ω=1,剩余系数λ=1,对过载节点采取不同的分配策略。在仿真中DD、SLD策略下的抗毁性相对较优,因此MD策略采取以上两种策略进行加权。通过测试发现当DD、SLD策略的权重分别取0.3、0.7时,MD策略相对较好,因此MD策略由DD、SLD两种策略加权所得。不同的过载节点负载分配策略仿真结果如图1所示。

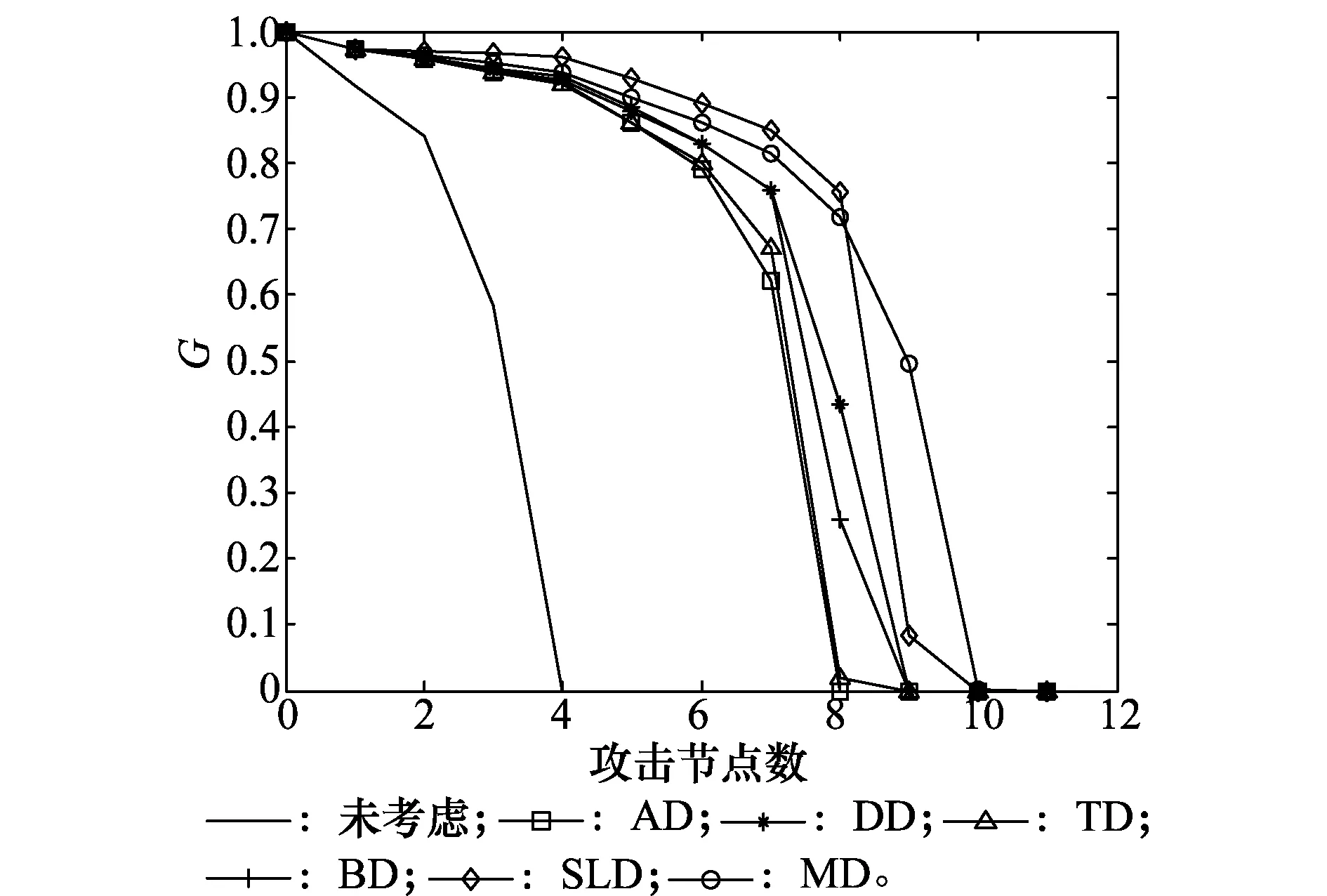
图1 不同过载节点负载分配策略下抗毁性对比图Fig.1 Comparison of invulnerability under different overload node load assignment strategies

由图1可知,未考虑过载节点负载分配策略时,由于超过容量的负载没能被及时分担使得节点更易失效,因此网络的抗毁性最差。AD策略是所有分配策略中效果最不理想的;而SLD策略与MD策略下的抗毁性均较佳。这是由于AD策略忽视了相连节点的差异性,剩余负载较小的节点存在着较高的失效风险。相反,SLD策略根据剩余负载进行分配,从而失效风险降低。此外,MD策略在攻击过程中均使得网络保持着较强的抗毁性,这是由于该策略一方面考虑了节点的度,即分散负载的能力,另一方面考虑了节点的剩余负载,即可承受负载的能力。因此,MD策略相对较佳。综上所述,对过载节点进行合理的疏导,能够增强网络的抗毁性,减少级联失效的影响。

3.2 过载系数对网络抗毁性的影响

为探究过载系数δ对网络抗毁性的影响,令过载节点负载分配策略为DD策略,分布系数ω=1,剩余系数λ=1。对过载系数δ取不同的值,仿真结果如图2所示。

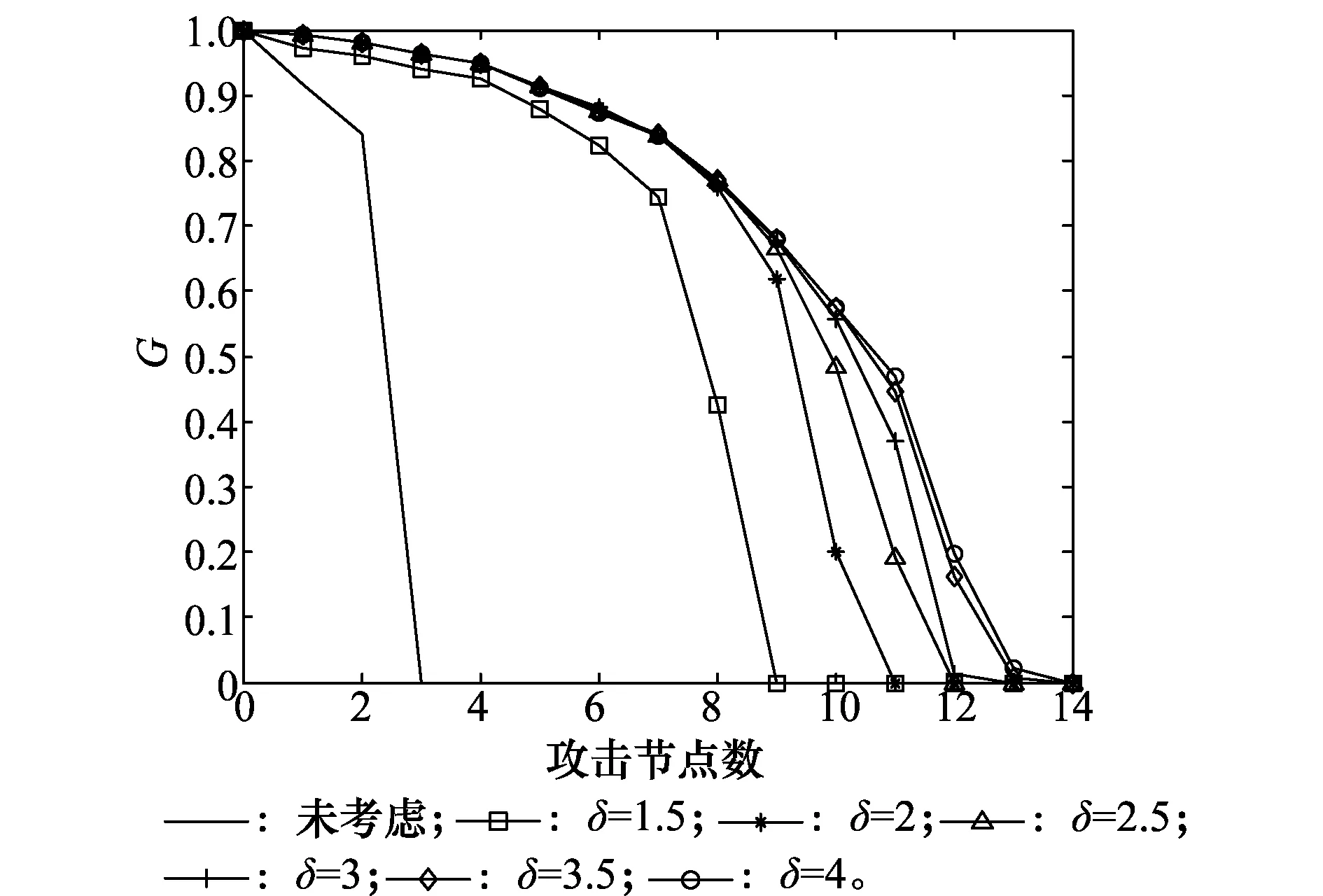
图2 不同过载系数下抗毁性对比图Fig.2 Comparison of resistance under different overload coefficient

由图2可知,当网络未考虑过载状态时,显然级联失效对网络的影响是较大的,仅攻击3次就已崩溃。但是当δ=1.5时,抗毁性相对于δ=1时有了显著提升,攻击9次之后才完全崩溃。随着δ增大,抗毁性总体上也呈现出了增强的趋势。这是由于δ越大,节点对于额外负载的处理能力也就越强,因此抗毁性有了一定提升。但是当δ=3.5,δ=4时,两者差距不大。

综上所述,当节点存在小范围的过载能力时,可显著提高抗毁性；而δ增加到一定程度时,其对抗毁性提升的贡献降低。现实网络中,提升节点的过载能力需考虑其构建成本,因此单纯增加δ是不合理的。

3.3 分布系数对网络抗毁性的影响

为研究分布系数ω对网络抗毁性的影响,令过载节点负载分配策略为DD策略,过载系数δ=1.5,剩余系数λ=1。对分布系数ω取不同的值以进行研究,仿真结果如图3所示。由图3可知,当攻击数少于4时,分布系数ω对抗毁性没有存在影响。当攻击数超过4时,ω=0.2的情况下级联失效对网络抗毁性所造成的影响最大,抗毁性呈现出直线下降的趋势;而ω=2与ω=2.5时,抗毁性均相对较强。随着ω的不断增大,抗毁性也在增强。这是由于当ω较小时,负载即使小部分超过其容量,也会造成较高的失效概率,从而易引起级联失效现象。因此，在实际网络中必须对分布系数较小的情况加以重视。当ω较大时,负载在一定范围内超过容量,节点失效概率仍可保持较小的状态,因此可有效遏制节点的失效个数,控制了级联失效对抗毁性的影响。

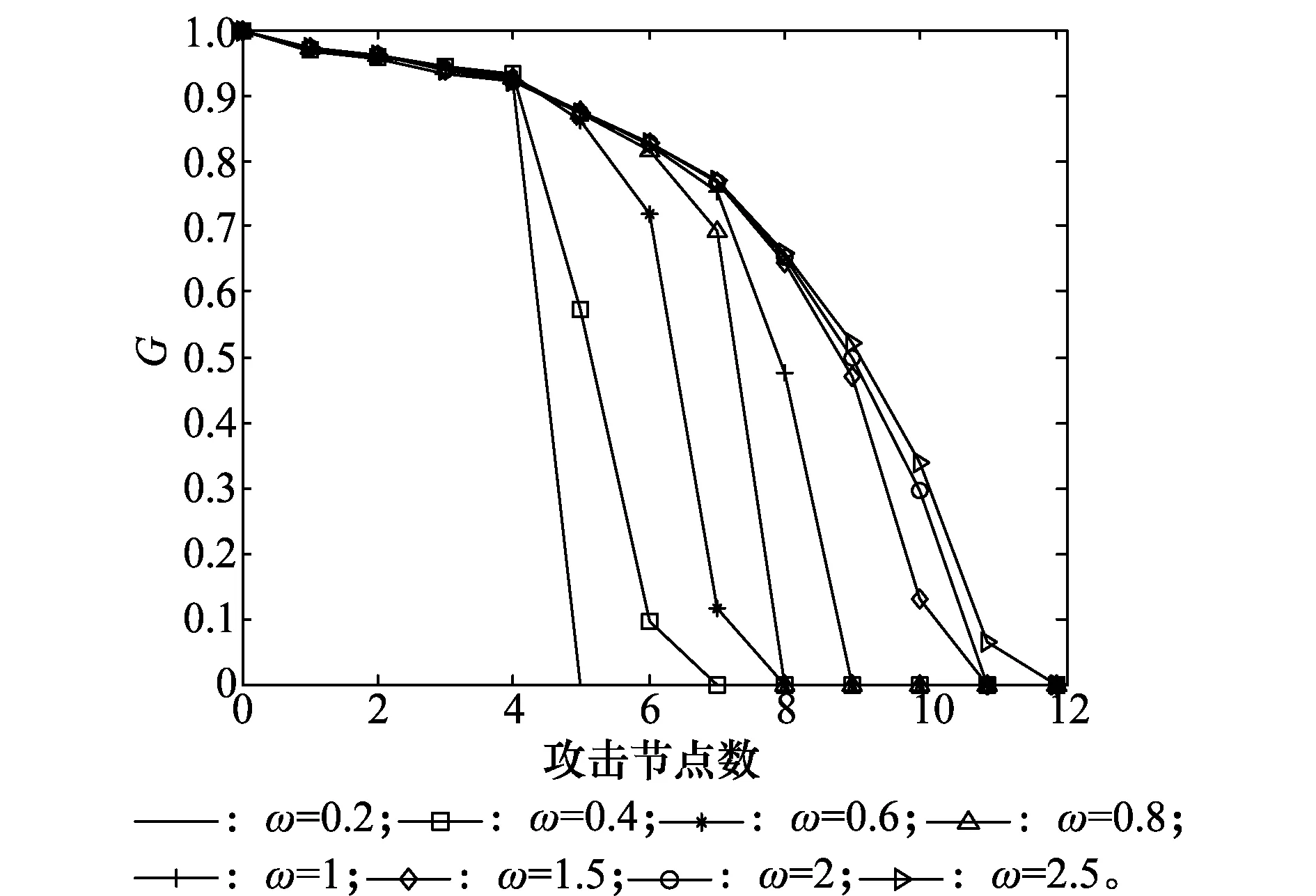
图3 不同分布系数下抗毁性对比图Fig.3 Comparison of damage resistance under different distribution coefficients

3.4 剩余系数对网络抗毁性的影响

为探究剩余系数λ对网络抗毁性的影响,令过载节点负载分配策略为DD策略,过载系数δ=1.5,分布系数ω=1,对λ取不同的值。由于在攻击次数小于4次时G的变化相似,因此只列出攻击次数为4～10次的图像,仿真结果如图4所示。

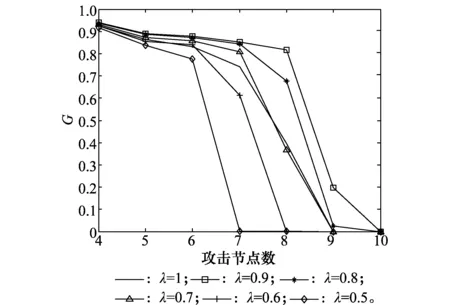
图4 不同剩余系数下抗毁性对比图Fig.4 Comparison of destruction resistance under different residual coefficients

由图4可知,当剩余系数λ=0.5时，网络的抗毁性最差,级联失效所造成的影响较大。而λ=0.9时,在攻击过程中抗毁性最强。这是由于λ决定着过载节点分配之后负载的剩余量。当λ较小时，过载节点分配至相连节点的负载较大,过载节点虽可变为正常状态,但易使相连节点过载或是失效；当λ较大时,过载节点分配至相连节点的负载较少,承担部分负载又易过载或失效。因此,λ存在某一值才能够使得节点保留一定的冗余能力来处理负载,同时又不会对相连节点产生过多影响。

由图4可知,在DD策略下λ=0.9时，网络抗毁性最强。为探究在不同的过载节点分配策略中,λ=0.9时抗毁性仍能否达到最强,因此令过载系数δ=1.5,分布系数ω=1,对不同的λ、过载节点负载分配策略进行仿真,蓄意攻击10个节点对G取平均值,仿真结果如图5所示。

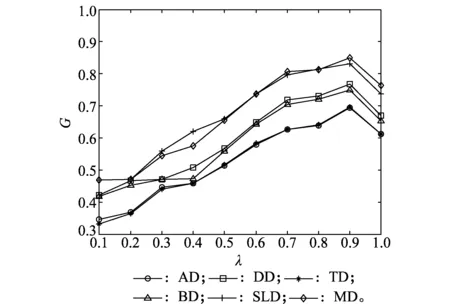
图5 不同剩余系数、过载节点负载分配策略下抗毁性对比图Fig.5 Invulnerability comparison of load distribution strategies with different residual coefficients and overload nodes

由图5可知,随着初期λ不断增大,不同策略下的抗毁性均呈现出上升趋势。并且当λ=0.9时,不同过载节点负载分配策略下的G取值0.6～0.9;而λ=0.1时,G仅维持在0.3～0.5。这表明对于m0=5、m=5的BA无标度网络而言,在不同的过载节点负载分配策略中λ=0.9时，网络的抗毁性相对较好。

3.5 过载节点负载分配策略与平均容忍系数关系

为探究不同过载节点负载分配策略与平均容忍系数的关系,令过载系数δ=1.5,分布系数ω=1,剩余系数λ=1,容忍系数增量Δα=0.01,最大迭代次数tmax=50,计算不同过载节点负载分配策略下平均容忍系数αc的值,结果如图6所示。

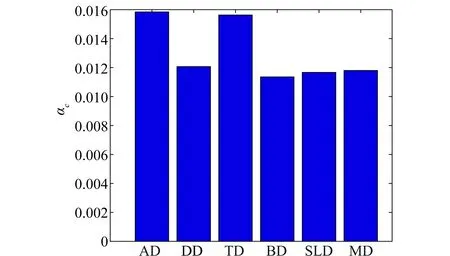
图6 不同过载节点负载分配策略下平均容忍系数对比图Fig.6 Comparison of average tolerance coefficients under different overload node load allocation strategies

由图6可知,在AD策略以及TD策略下网络的平均容忍系数αc均较高。这是因为网络中节点紧密度的值差异较小,所以两者的结果相似。而在DD、BD、SLD、MD这4种策略中,αc的值均在0.012之下,显著低于AD策略以及TD策略。这是由于在AD策略以及TD策略下,过载节点的负载会较为平均地分配至与其相连的节点,为了避免产生级联失效现象,容量较小的节点需拥有较大的容忍系数,因而其他4种策略可使得网络的构建成本较低。此外,由图6可知，BD策略下的αc值略小于其他策略。通常,网络的构建成本与αc存在着正相关的关系，这表明过载节点采取AD策略、TD策略,其网络的构建成本较高,而其他4种策略均可使网络构建成本较低。