免调度NOMA系统中扩频码优化设计
2022-09-20何雪云杨卓勋孙林慧
何雪云,杨卓勋,孙林慧
(南京邮电大学通信与信息工程学院,江苏 南京 210003)
为了应对正交多址接入(Orthogonal Multiple Access,OMA)技术的局限性,能够满足未来场景对大规模连接和高吞吐量需求的非正交多址接入(Non-Orthogonal Multiple Access,NOMA)技术应运而生[1]。在基于多重测量向量压缩感知(Multiple Measurement Vector-Compressive Sensing,MMV-CS)框架的免调度NOMA系统中,压缩感知重建算法用于联合解决信道估计(Channel Estimation,CE)和多用户检测(Multiuser Detection,MUD)问题[2],扩频码本正好对应于CS模型中的测量矩阵。针对NOMA系统上行链路免调度传输,3GPP Rel.16标准化了两阶段随机接入技术,此技术将前导码和数据组合成单个消息由用户发送给基站,随后基站将接入响应发送给用户,本文研究的问题属于技术的第一阶段。扩频码本的最大互相关值用μ表示,文献[3]中提出了互不相干性质(Mutual Incoherence Property,MIP),认为扩频码本的μ值越小则越利于稀疏信号重建。因此在CS理论框架下优化扩频码本可以提高系统性能。
扩频码本的选择对NOMA系统的性能具有较大的影响[4],文献[5]采用了三元复序列码本作为扩频码本,文献[6]提出了五元复序列扩频码本,有效减少碰撞现象的发生。文献[7]对复序列扩频码本进行了优化,提升了系统的性能,文献[8]选取高斯随机矩阵作为扩频码本,文献[5-6]中扩频码本包含元素0,会导致用户数据的丢失,文献[7-8]中扩频码本的μ值还不够低,码本有进一步优化空间。本文针对码本维度取特定值的情况,具体研究了多种μ值满足Welch界的最优码本,认为文献[9]研究的码本限制条件更少,构造更灵活,适合用作NOMA系统的扩频码本;针对码本维度可变的情况,本文提出了双重迭代最小化μ值算法,采取优化门限并行取值策略,通过双重迭代不断降低起始码本各列之间的互相关值从而达到码本的优化,最终得到的扩频码本μ值明显降低。文献[10]针对免调度NOMA系统采用压缩感知重建算法联合解决CE和MUD问题,我们将本文算法优化获得的扩频码本应用于文献[10]的系统模型,并同样采用文献[10]所提CE和MUD联合解决算法进行仿真测试。仿真结果表明,与其他现有扩频码本相比,本文获得的优化扩频码本能够明显改善系统的CE和MUD性能。
1 基于MMV-CS框架的免调度NOMA系统模型
假设上行免调度NOMA系统中拥有一个基站和N个用户,所有用户均假定只有一根天线。在任意时间区间内,系统内只有少量K个活跃用户,其他用户则处于非活跃状态。不失一般性,我们考虑信道为平坦瑞利衰落信道,同时假设用户在一个帧结构中处于同步状态,用户状态在一帧中保持不变,稀疏帧的传输模型如图1所示。
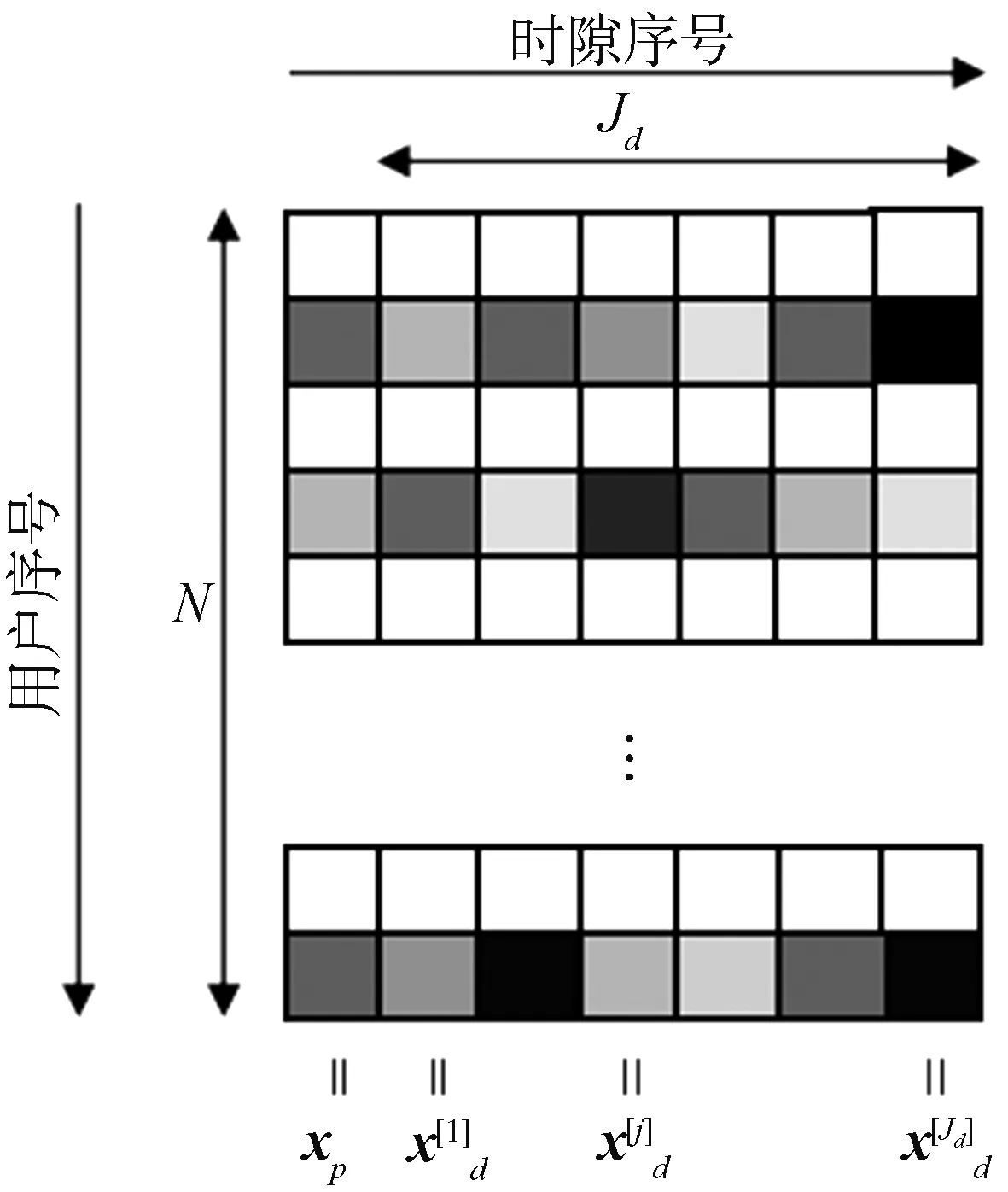
图1 稀疏帧的传输模型

式中:S∈ CM×N,X∈ CN×J,Z∈ CM×J,Y∈ CM×J,J=Jd+1,由于h与a[j]d具有相同的支撑集,少量非零元素所在行索引等于激活用户序号。因此,式(2)为一个MMV-CS问题。矩阵X各列具有联合稀疏性,扩频码本S对应于CS理论中的测量矩阵,s又称为扩频矩阵。
2 基于差集序列与变换矩阵的扩频码本优化方法

针对特定维度的扩频码本,其行索引集合只要属于差集合,根据式(5)构造的码本皆可达到Welch界,本文选取构造的码本WΦ作为特定维度的扩频码本Sopt。 以参数为(307,18)的扩频码本为例,相比高斯随机扩频码本和三元复扩频码本,由式(5)构造的扩频码本能够明显改善系统的性能。
3 双重迭代最小化μ值的扩频码本优化方法
由于特定维度的扩频码本受限于差集合,而差集合的参数(p,k,λ)限制了差集合的构造,即很多维度的最佳码本不存在。本节针对任意维度设计扩频码本,提出一种双重迭代最小化μ值算法,在双重迭代中不断降低起始码本W各列之间的互相关值从而达到对码本W的优化,Gamma矩阵G定义如下
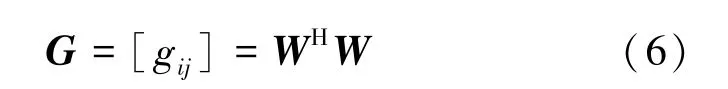
式中:W为列归一化后的形式,G的非对角线元素为码本W不同列的内积,码本的μ值为非对角线元素的最大值,即为降低码本 W 各列之间的互相关性,文献[8]提出了一个迭代算法,在每次迭代中对矩阵G的元素采用下式进行缩减
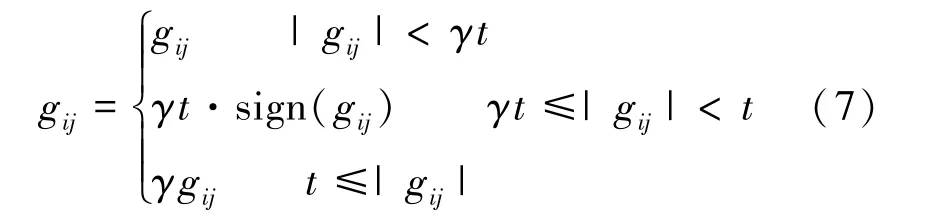
式中:t为优化门限且为一个定值,γ为缩减因子且0<γ <1。 缩减之后的矩阵G记为,若的秩大于W的行数,则用奇异值分解(Singular Value Decomposition,SVD)降秩,然后进行平方根分解得到优化后的码本。
文献[12]借鉴文献[8]Elad算法的思想提出了一种大规模MIMO系统中的导频优化方法。本文通过改进Elad算法提出双重迭代最小化μ值的扩频码本优化方法。本文算法的改进体现在以下3个方面:(1) 关于起始码本,文献[8]和文献[12]均选取高斯随机矩阵,本文选取部分Zadoff-Chu复矩阵。因为在仿真研究中发现,起始优化码本选择部分Zadoff-Chu复矩阵可以保证算法收敛性,同时获得μ值更低的扩频码本。(2)文献[8,12]的作者使用的优化门限t均为定值,而通过研究发现,优化门限t选取不同,最终获得的优化码本的μ值不同。因此,本文采取t的并行取值策略来提升优化效果,即从优化门限序列中选出最适合当前码本的优化门限t,优化得到此时最优的扩频码本。(3)与文献[8,12]的单层迭代算法不同,本文结合t的并行取值,采取双重迭代。在每一轮迭代中,针对相同的码本W,对优化门限t并行取L个值并分别进行G矩阵缩减迭代操作,即可得到L个优化矩阵,选择其中μ值最小的矩阵作为本次迭代的优化码本Xiter。 将码本Xiter再作为下一轮迭代的起始码本,重新进行优化门限t并行取值的G矩阵缩减迭代操作。重复上述步骤直到优化码本的μ值基本不变时算法停止,得到最终优化的扩频码本Sopt。因为G矩阵缩减本身为迭代操作,本文结合优化门限t的并行取值又增加了一层迭代,因此称为双重迭代算法。仿真表明,本文优化后获得的扩频码本μ值相比文献[8]更低且接近Welch界。完整的双重迭代最小化μ值算法步骤如下。
算法1 双重迭代最小化μ值算法

4 仿真结果和分析
本文在 CPU型号为 Intel(R)Core(TM)I5-6300HQ,速度为2.30 GHz,内存为8 GB RAM的联想笔记本上运行Matlab2021b进行仿真实验。仿真分为两部分:第一部分用双重迭代最小化μ值算法对部分Zadoff-Chu矩阵进行优化,分析扩频码本优化效果;第二部分,通过仿真分析本文所提扩频码本优化方法对文献[10]免调度NOMA系统基于MMV-CS框架的CE和MUD联合算法的性能提升效果。
4.1 双重迭代最小化μ值算法对扩频码本μ值降低的效果分析
本节首先将文献[8]采用的高斯随机码本、文献[5]采用的三元复扩频码本和本文提出的双重迭代最小化μ值算法优化获得的扩频码本进行比较,码本长度为50,扩频码本数量分别为200、400、600、800,3种扩频码本μ值分布如图2所示。从μ值大小来看,在码本长度不变的情况下,随着扩频码本数量的增加,3种码本μ值不断增加,以扩频码本数量为200为例,高斯随机码本μ值为0.550 5,三元复扩频码本μ值为0.442 5,本文算法优化得到的扩频码本μ值为0.131 1,相比高斯随机码本下降了76.19%,相比三元复扩频码本下降了70.37%,本文优化得到的扩频码本μ值相比另外两种是最低的且接近Welch界。
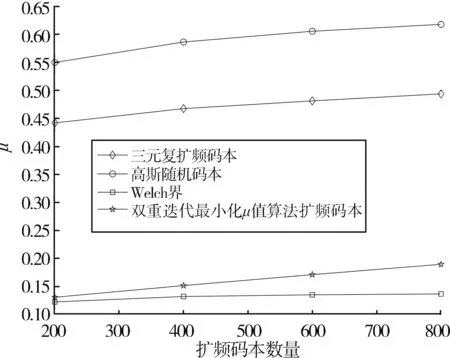
图2 3种扩频码本的最大互相关幅值比较
接着比较本文提出的双重迭代最小化μ值算法与使用文献[8]算法对同一起始码本的优化结果。以码本维度为[50,200]的扩频码本为例,其中50表示扩频码本长度,200表示扩频码本数量,两种算法得到的扩频码本μ值如表1所示,由表1可知,文献[8]算法在迭代收敛后μ值保持0.190 0不变,本文算法由于使用双重迭代,可以使μ值继续降低最终收敛达到了0.131 1,μ值下降了31%,相比文献[8]更低且接近Welch界。
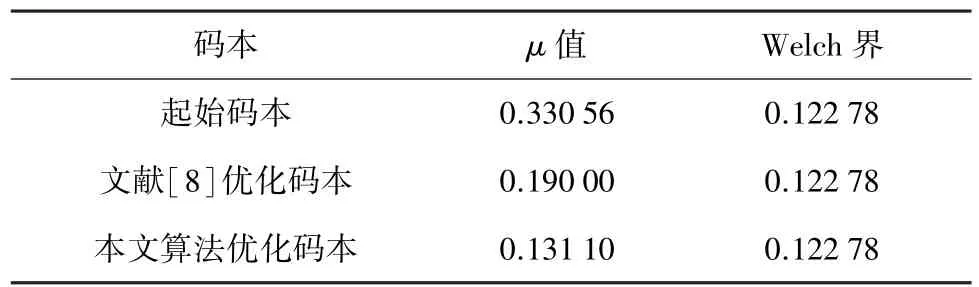
表1 两种不同算法优化后的扩频码本最大互相关值比较
4.2 不同扩频码本在NOMA系统联合CE和MUD问题中的性能分析
文献[10]针对免调度NOMA系统提出了一种基于MMV-CS框架的CE和MUD联合算法。本节在文献[10]的系统模型中分别使用高斯随机码本、三元复扩频码本和本文所提算法优化后的扩频码本,仿真对比分析三者所获得算法的性能差异。仿真参数设置如下:信道为平坦瑞利衰落信道;1个时隙发送导频数据,6个时隙发送信息数据;调制方式为QPSK。仿真比较的性能参数指标如下:误符号率(Symbol Error Rate,SER),成功活跃用户检测率(Successful Activity Detection Rate,SADR),即成功检测的活跃用户数占总活跃用户数的比例,信道估计的归一化均方误差(Normalized Mean Square Error,NMSE),其中NMSE 计算表达式为
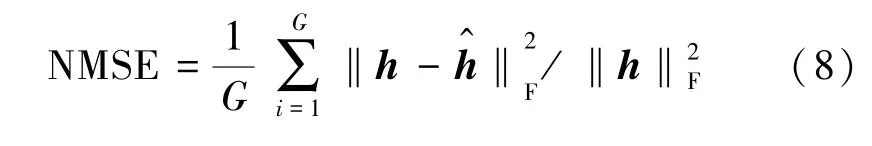
式中:h为信道系数,表示信道系数估计值,G为仿真次数。
4.2.1 基于差集序列与变换矩阵优化的扩频码本性能
本小节比较维度取特定值的扩频码本:扩频码本长度为18,扩频码本数量为307,活跃用户数k取8、10。图3为维度取特定值时3种扩频码本的误符号率曲线,在相同活跃用户数、相同信噪比时,采用ZC扩频码本相比使用另外两种扩频码本误符号率最低。比如当活跃用户数为8、信噪比为30 dB时,ZC码本SER值为1.3×10-3,相比三元复码本SER值为2.3×10-3降低了43.48%,相比高斯随机码本SER值为1.35×10-2降低了90.37%。
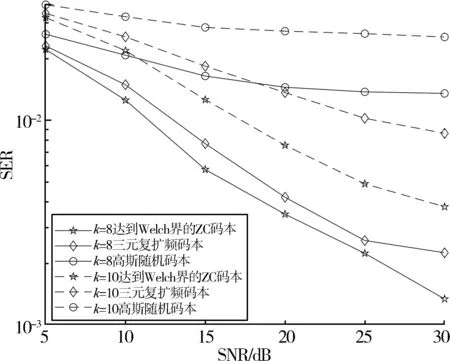
图3 维度为[18,307]扩频码本的SER值比较
图4所示为3种扩频码本在不同信噪比下和不同活跃用户数下的成功活跃用户检测率。从图4可以看出,在相同活跃用户数、相同信噪比时,ZC扩频码本相比另外两种扩频成功活跃用户检测率是最高的。当活跃用户数为10、信噪比为30 dB时,ZC码本SADR值为94.55%,相比三元复码本SADR值为79.75%,而高斯随机码本SADR值仅为49.15%,成功活跃用户检测率不足一半。
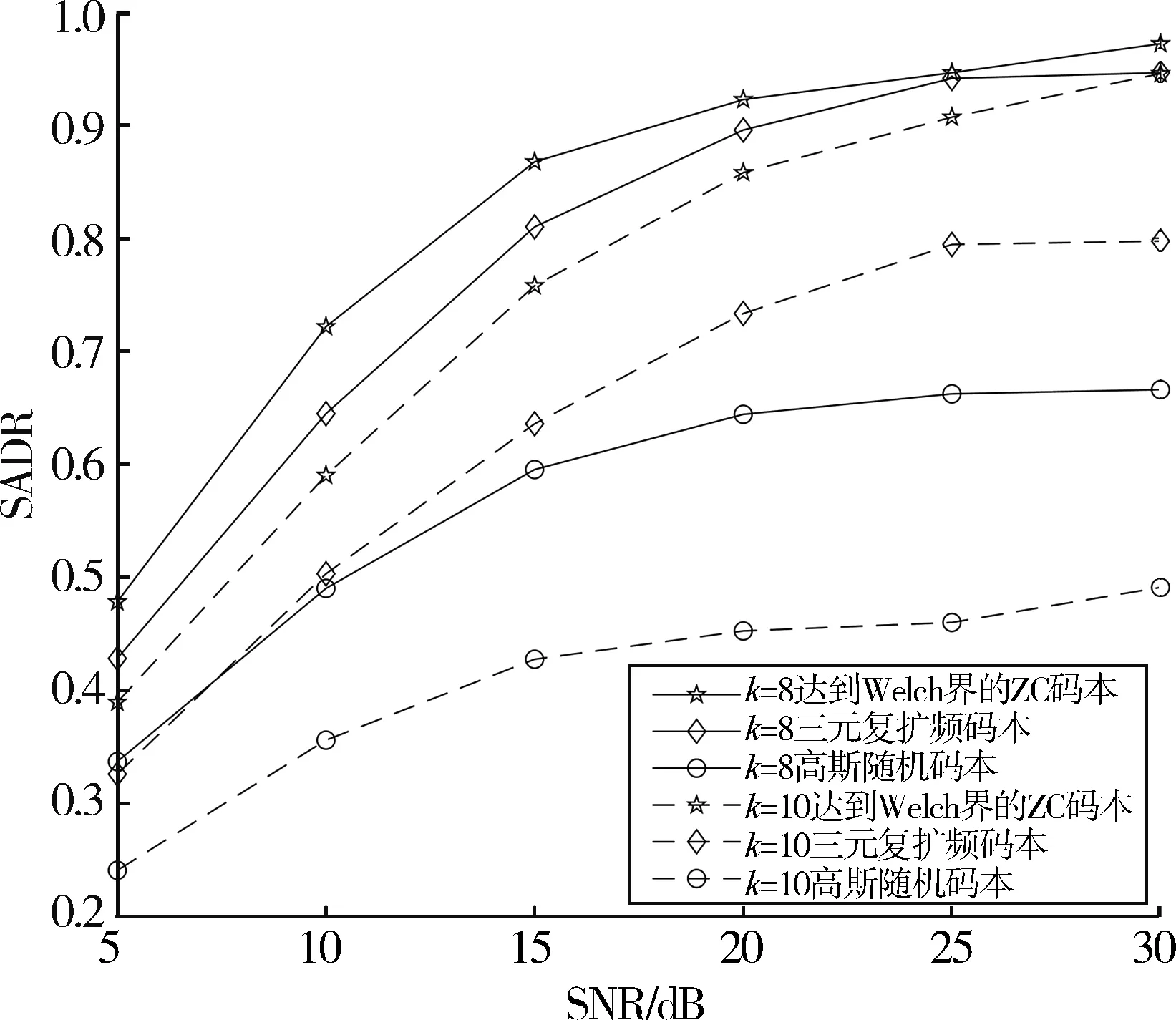
图4 维度为[18,307]的扩频码本的SADR值比较
图5所示为3种扩频码本的NMSE仿真结果。结果表明,在相同活跃用户数、相同信噪比时,使用ZC扩频码本相比另外两种扩频码本,信道估计的NMSE值均有明显下降;在相同信噪比时,随着活跃用户数的增加,使用ZC扩频码本相比另外两种扩频码本NMSE值上升较小。例如信噪比为30 dB时,使用 ZC扩频码本时的 NMSE从k=8时的7.28×10-2到k=10 时的 8.40×10-2,仅上升了15.38%,而高斯随机码本从k=8时的0.568 3到k=10时的1.324 1,上升了132.99%。
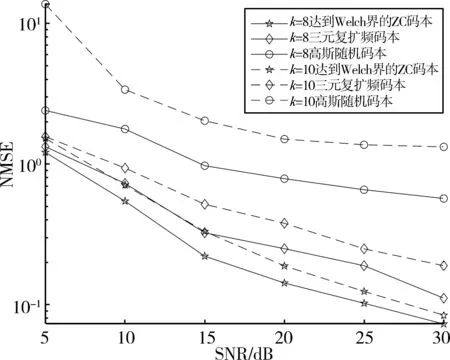
图5 维度为[18,307]的扩频码本的NMSE值比较
4.2.2 双重迭代最小化μ值算法优化的扩频码本性能
本小节比较维度可调的扩频码本:扩频码本长度为 50,扩频码本数量为 200、400、600、800,活跃用户数k取 10、20、30。
以扩频码本数量为200进行性能分析,图6为3种扩频码本的误符号率曲线,可以看出在相同活跃用户数、相同信噪比时,使用本文算法优化得到的扩频码本使系统误符号率最低。当活跃用户数较大时,使用本文算法优化得到的扩频码本对系统误符号率的改善更加明显。
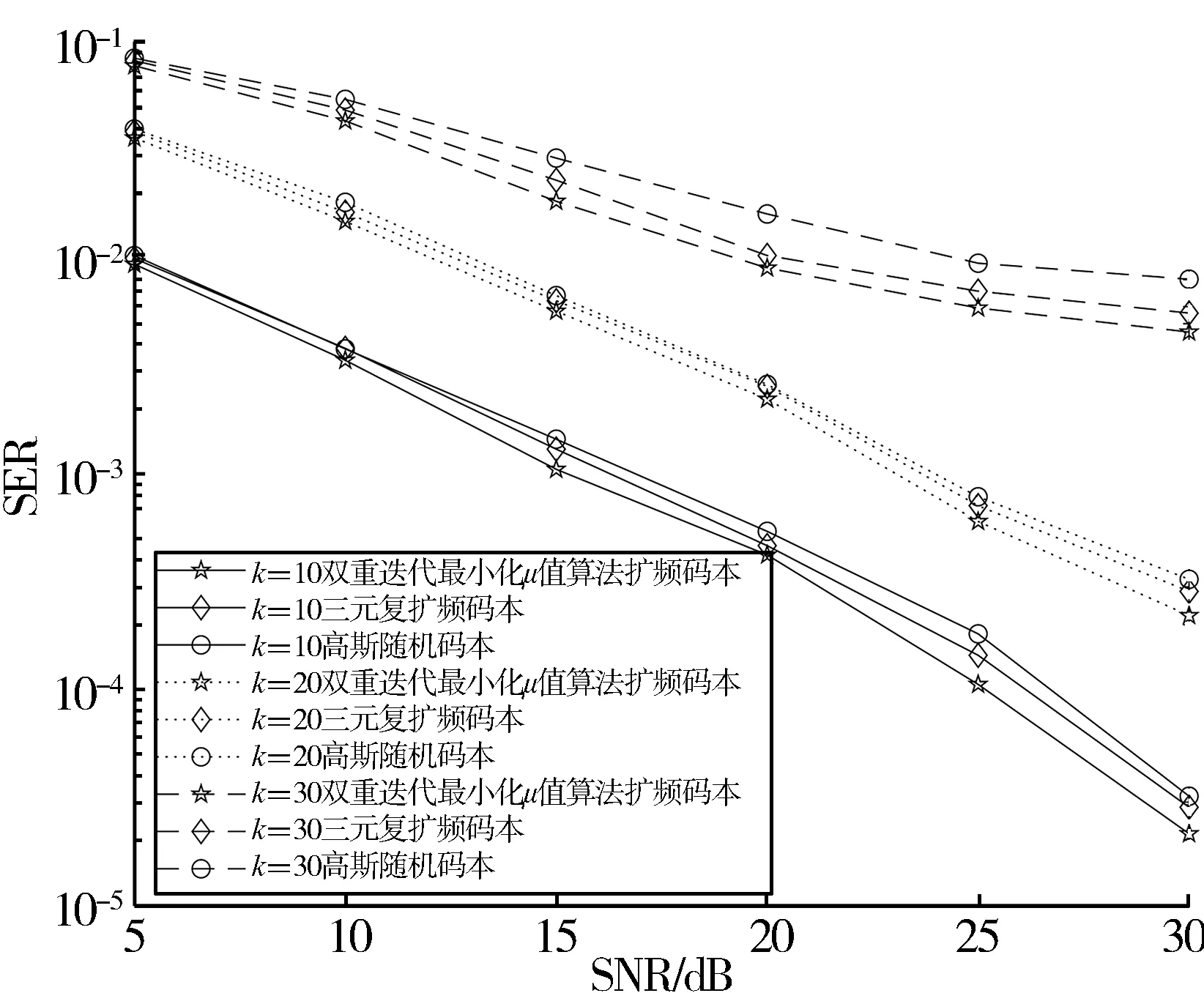
图6 维度为[50,200]扩频码本的SER值比较
图7所示为使用不同扩频码本时的成功活跃用户检测率曲线,图中可以看出,在相同活跃用户数、相同信噪比时,使用本文算法优化得到的码本相比另外两种码本成功活跃用户检测率是最高的。随着活跃用户数的递增,使用本文算法优化得到的码本对成功活跃用户检测率的改善更加明显。
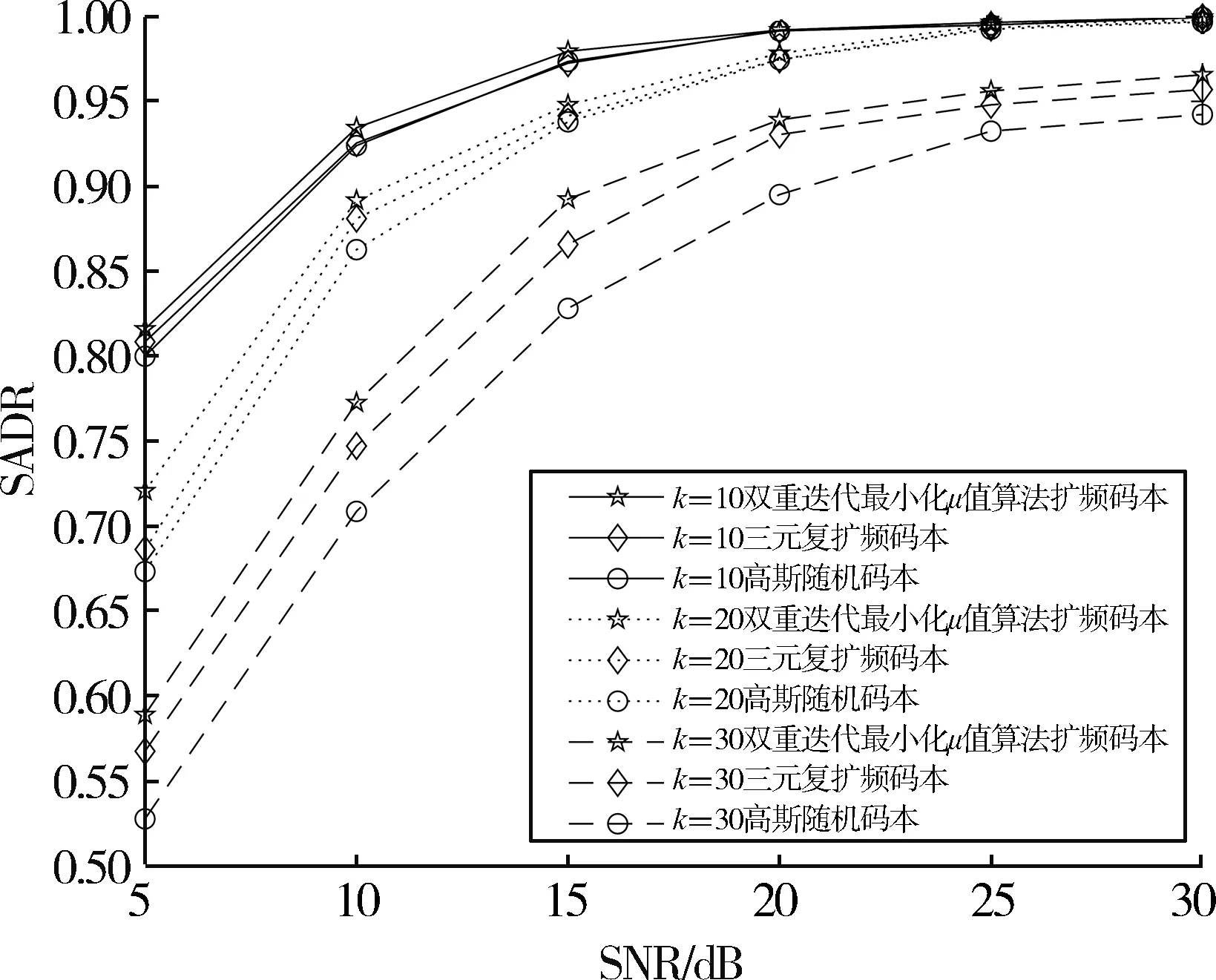
图7 维度为[50,200]扩频码本的SADR值比较
图8所示为使用3种扩频码本的NMSE仿真结果。结果表明,在低活跃用户数时,3种扩频码本的NMSE性能相接近。随着活跃用户数的不断增加,使用本文算法得到的码本对NMSE的改善最明显。接下来取活跃用户数为20,信噪比为15 dB,码本长度为 50,码本数量分别为 200、400、600、800来进行不同扩频码本的系统性能分析。图9、10和11分别是系统误符号率曲线、成功活跃用户检测率曲线和信道估计NMSE曲线。从仿真结果来看,随着码本数量的不断增加,系统SER逐渐上升,SADR不断下降,NMSE不断上升。使用本文算法优化得到的扩频码本相对于其他两种码本而言,能使系统获得更低的SER、更高的SADR和更低的NMSE。

图8 维度为[50,200]扩频码本的NMSE值比较
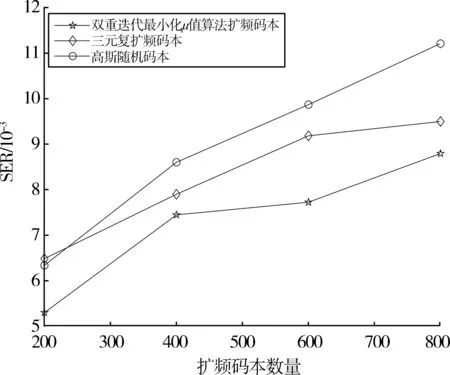
图9 不同码本数量的扩频码本的SER值比较(活动用户数k=20、信噪比SNR=15 dB)
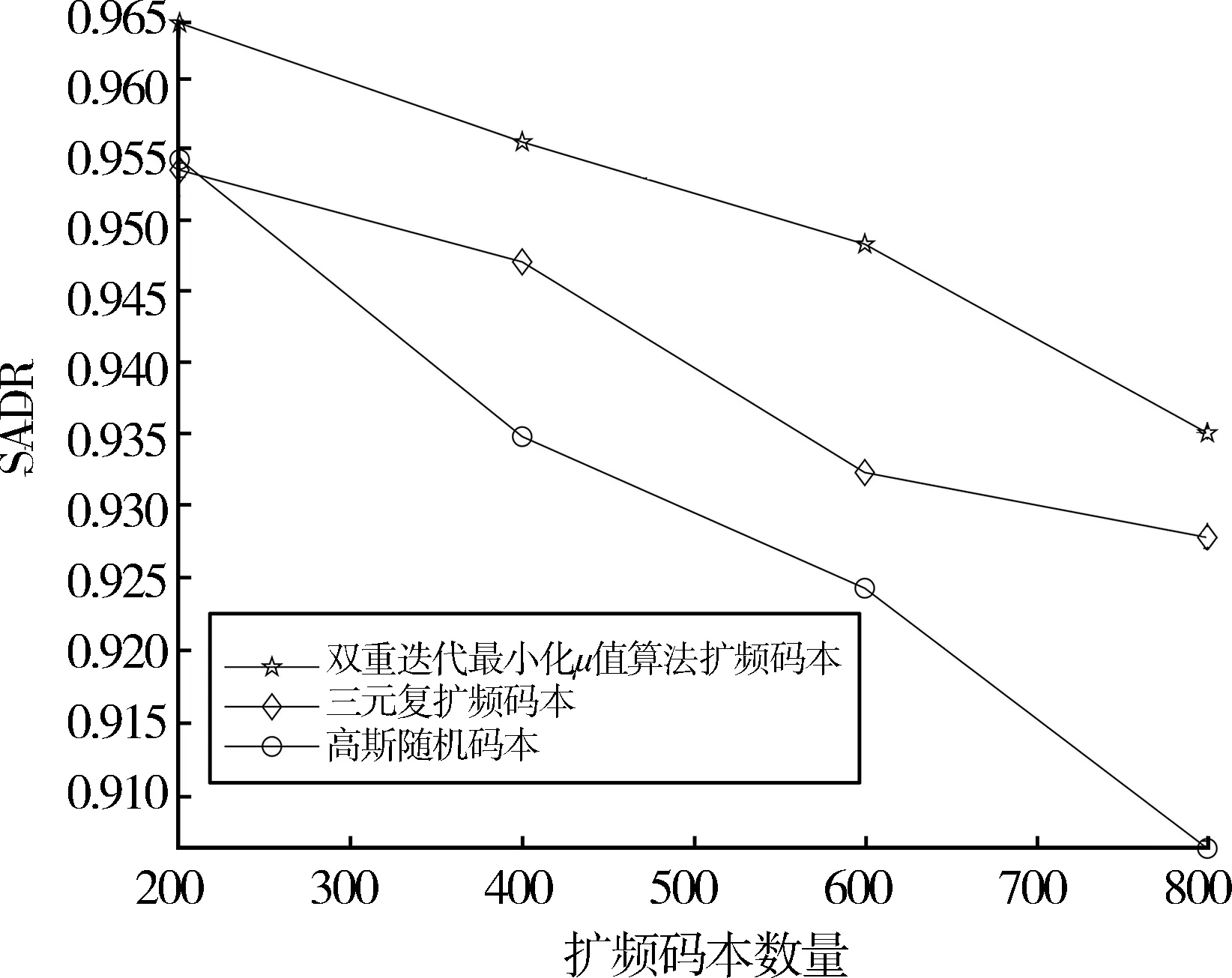
图10 不同码本数量的扩频码本的SADR值比较(活动用户数k=20、信噪比SNR=15 dB)
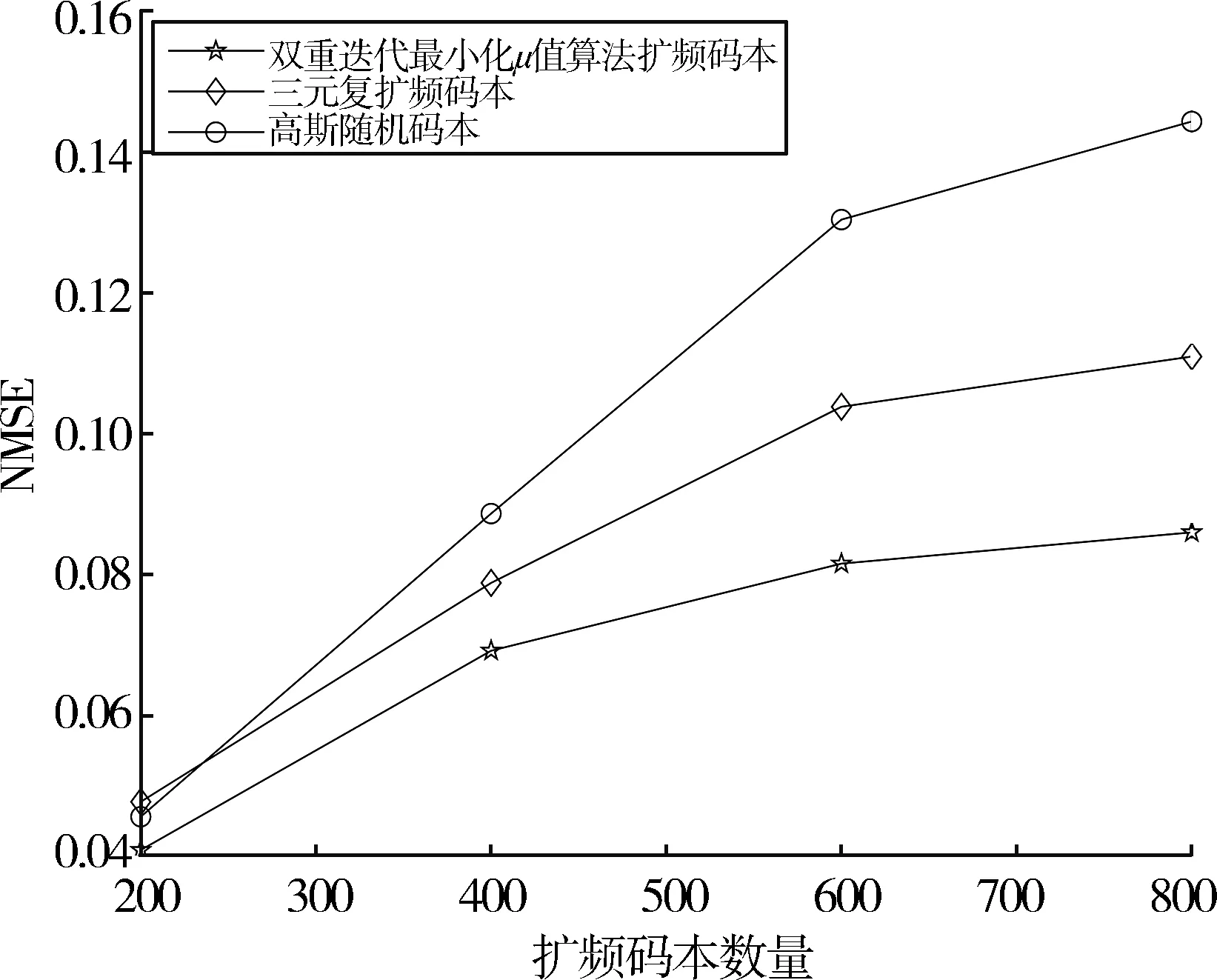
图11 不同码本数量的扩频码本的NMSE值比较(活动用户数k=20、信噪比SNR=15 dB)
5 结束语
本文研究了免调度NOMA系统中的扩频码本设计问题。笔者认为,在码本维度参数符合差集合参数时,可通过Zadoff-Chu矩阵构造达到Welch界的扩频码本。为了寻求任意维度低互相关幅值扩频码本的构造方法,本文提出了一种双重迭代最小化μ值算法。算法采取并行取值策略,通过双重迭代不断降低码本各列之间的互相关值,从而实现码本的优化。仿真结果表明,在基于MMV-CS框架下的NOMA系统中,本文算法优化获得的扩频码本相比三元复扩频码本和高斯随机扩频码本,能够获得更优秀信道估计和多用户检测性能。
