大规模MIMO中继系统基于LoS的等增益传输方案

岳殿武, 孟子琦, 孙 玉, 闫秋娜

(1. 大连海事大学信息科学技术学院, 辽宁 大连 116026;2. 北京通广龙电子科技有限公司, 北京 100094)

0 引 言

大规模多输入多输出(multiple input multiple output, MIMO),可以大幅度提高蜂窝系统的频谱效率和能量效率[1-2],故成为面向5G最具发展前景的新技术之一[3-4]。

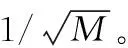
莱斯衰落模型,适用于具有莱斯视距(line-of-sight, LoS)传播的环境,除了应用于传统微波中继系统和卫星通信系统外,还可以应用于小蜂窝网络和毫米波通信[6-9]。特别,其中的毫米波通信是面向5G最富有发展前景的技术之一[10]。明显不同于瑞利衰落信道,莱斯衰落信道是由LoS分量和散射分量两个信道分量构成。和散射分量相比,很容易估计与LoS分量相关的信道信息。这启发我们形成一个有效避免导频污染问题的思路:忽略莱斯衰落环境下的散射分量,只基于LoS分量进行信号处理。为此,对于接收端和发送端都配置有大规模多天线的单用户系统,在文献[11]中提出了一个仅基于LoS分量的等增益合并(equal gain combining, EGC)与等增益传输(equal gain transmission, EGT)相结合的系统方案。对于所提出的方案,只要接收端和发送端的天线数趋于无穷大且保持一个固定的比例,文献[11]指出,如果发射功率按发送端和接收端的天线数的乘积成比例的缩小,与具有理想CSI下MRC/MRT方案相比,两个方案的可达速率可以渐近相等。受上述结果的鼓舞,对于分布大规模MIMO的多用户上行系统,在文献[12]中继续研究了只基于LoS分量的线性传输方案的可达速率,并获得了几个功率缩放律。

值得一提的是,在莱斯衰落中,LoS分量是缓慢变化,而散射分量是快速变化的。从统计角度看,LoS分量是快衰落莱斯随机变量的一阶统计。因此,在信道估计时,对于与LoS分量相关的CSI很容易准确估计,且总体花费时间会明显少于对全部瞬时CSI估计所用的时间。 鉴于此,在LoS分量较强的环境下,基于LoS分量的线性传输方案反而会有更高的频谱效率。

众所周知,在无线通信中,对于较长的通信距离,中继技术可以将其分隔成几段较短的通信距离,从而可以使传输能量显著下降。在蜂窝通信网络中引入中继,就可以降低系统费用、消除覆盖盲点、扩大基站覆盖范围。因此中继技术是无线通信领域中值得发展的重要技术之一。特别是其中的双向中继技术,可以克服半双工模式的缺点,显著地提高频谱效率,因而近年来得到了学术界的广泛关注[13-17]。最后值得一提的是,双向中继比较适合中继和终端距离较小时的情况。因此,面向实际应用,更宜采用比较复杂的莱斯衰落模型而不是比较简单的瑞利衰落模型来进行探讨。

综上讨论,将中继技术、莱斯信道和大规模MIMO结合考虑会成为5G发展中的一个比较重要的研究课题[18-25]。在这个重要课题中,本文着重探讨基于LoS分量的EGC/EGT方案。

1 系统模型与基于LoS的传输方案

图1显示一个多用户双向MIMO中继系统。该系统有K对单天线用户,它们通过分布有M(M≥1)个天线的中继来相互交换信息。记第i个通信对为(2i-1,2i)(i=1,2,…,K),其中(k,k′)代表通信对用户k和用户k′。所有用户都有相同的传输功率并表示为PS,而中继端的传输功率表示为PR。

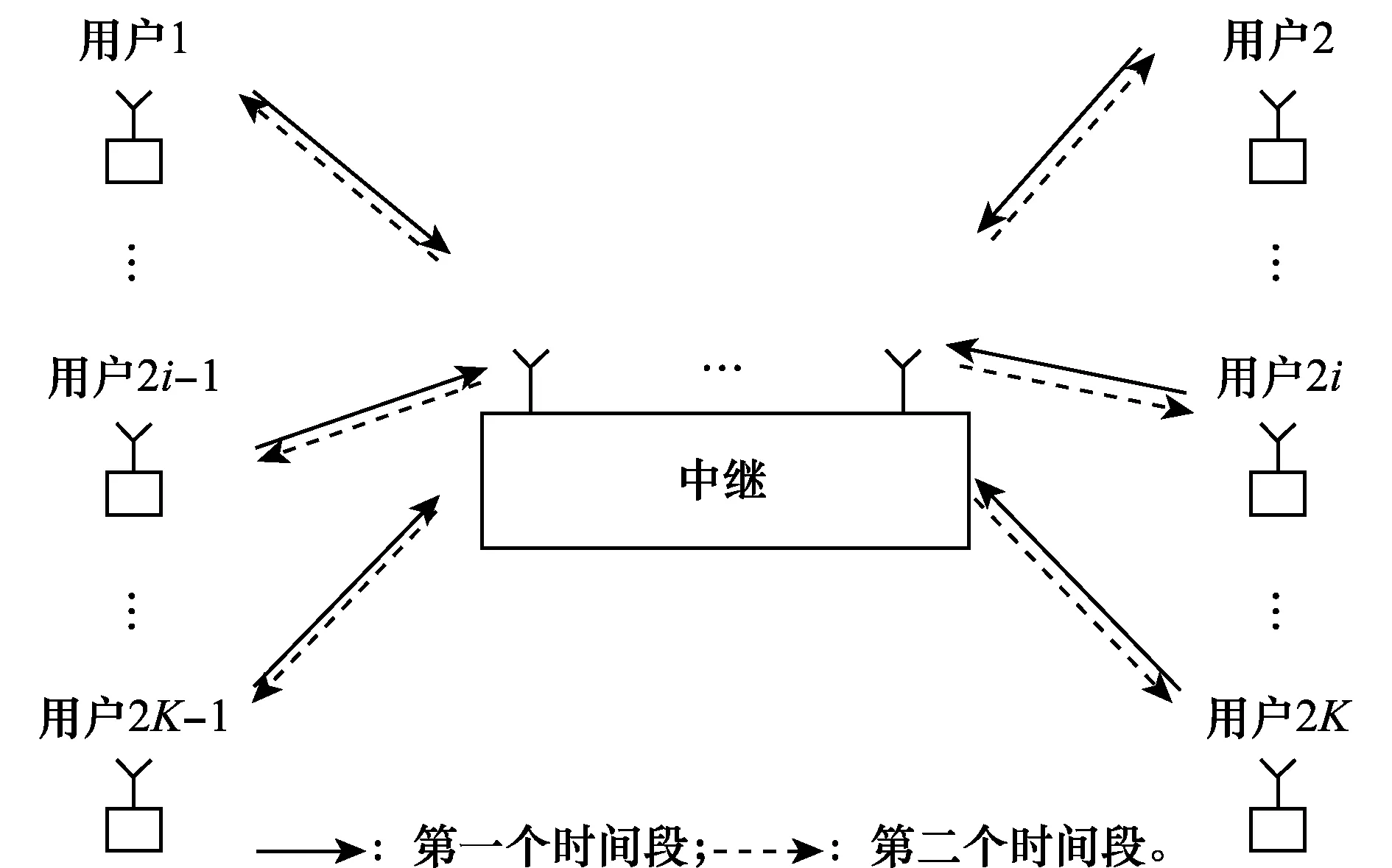
图1 系统模型Fig.1 System model

整个多对双向中继系统的通信过程要分两个时间段来完成。多址接入阶段是第一个时间段。在这个时间段,所有用户采用相同频率同时向中继发送数据。 此时,接收到的中继信号可表示为

(1)

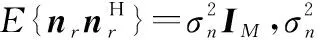
中继端和第k个用户之间的信道向量gk由LoS分量和散射分量两部分组成,根据文献[2]可表示为

(2)

式中,hk=[h1k,h2k,…,hMk]T；hmk表示第k个用户的发射天线到中继端的第m根天线间的小尺度衰落系数；βk=μk·νk表示第k个用户的发射天线到中继端的天线阵的大尺度衰落系数,其中，μk代表路径损耗,νk代表阴影衰落(服从对数正态分布),βk值随时间变化很慢[2，5]。

对于第k个用户,其莱斯因子定义为LoS分量和散射分量的功率之比,用ϑk表示。 则hk可以更进一步的分解为

(3)

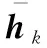
在本文的分析中,将考虑一般的莱斯链路(即有ϑk>0)。对于均匀线性阵列,LoS分量可以表示[26]为

(4)

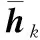
现在考虑第二个时间段。在第二个时间段,中继主要工作就是放大接收到的信号并向用户转发。众所周知,放大后的信号必须要符合功率限制的要求。即有PR=Tr(E{Fr(Fr)H}),其中,F∈CM×M表示中继端的波束成形矩阵。让A表示下行信道矩阵。则所有用户接收到来自中继端的信号可以一起表示为

y=ATFr+z

(5)

把式(1)代入到式(5)可得

(6)

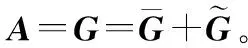
(7)

Rk=

(8)

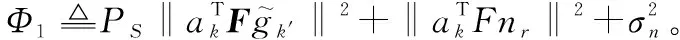
(9)

(10)

最后值得一提的是,在硬件实现复杂度方面,EGC/EGT却比MRC/MRT有明显优势。这是因为EGC/EGT可采用便宜的功率放大器和数模变换器,从而有效降低射频链路的花费,这对需要分布数百个天线的大规模MIMO系统而言尤为重要。

2 可达速率性能分析

在可达速率的分析过程中,同文献[6]一样,本文也假定传输功率参数ES和ER固定。本文将分析4种功率分配方案,其中后3种方案的传输功率均按中继天线数大小成比例缩小。

情况1用户没有功率缩小而中继也没有功率缩小,即PS=ES,PR=ER;

情况2用户进行功率缩小而中继没有功率缩小,即PS=ES/M,PR=ER;

情况3用户没有功率缩小而中继进行功率缩小,即PS=ES,PR=ER/M;

情况4用户进行功率缩小而中继也进行功率缩小,即PS=ES/M,PR=ER/M。

2.1 单对系统性能分析

为了便于推导和比较,首先分析单对双向AF系统,即假定K=1。不是一般性,在此假定k=1,则与之相对应的k′=2。则式(8)可表示为

(11)

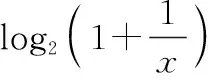
(12)

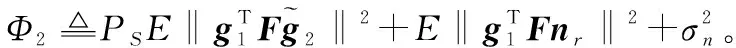
(13)

式中,1j(j=1,2)表示一个1×2的向量,其第j列是1,其他列全为0。类似地可推出

(14)

(15)

(16)

(17)

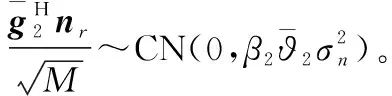
根据文献[12]中的式(30)～式(33)以及本文式(11)～式(17),得

(18)

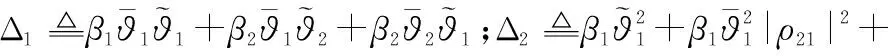
(19)

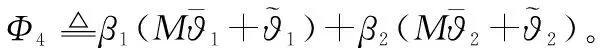
接下来分4种情况对式(18)进行分析。

情况1把PS=ES和PR=ER代入到式(18)中,并令M→∞,则可得

(20)

情况2把PS=ES/M和PR=ER代入到式(18)中,有

(21)

情况3把PS=ES和PR=ER/M代入到式(18)中,则

(22)

情况4把PS=ES/M和PR=ER/M代入到式(18)中,式(18)变为

(23)

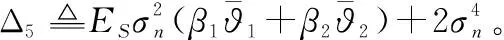
2.2 多对系统性能分析

第2.1节给出了单对双向AF中继系统的速率渐近分析。现在将之推广到多对场景。此时,式(8)可写成为

Rk=

(24)

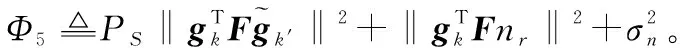
下面考虑给出(24)的近似表达式。 对式(24),再次利用詹森不等式和log2(1+x-1)的凸函数性质得

(25)

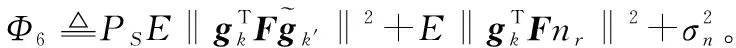
(26)

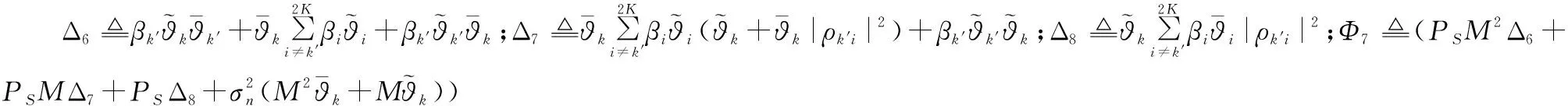
(27)

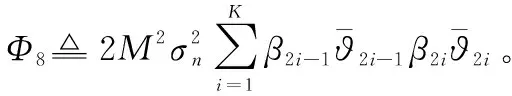
接下来对式(26)根据4种情况进行分析。

情况1把PS=ES和PR=ER代入到式(26)中,并令M→∞,则可得

(28)

情况2把PS=ES/M和PR=ER代入到式(26)中,则式(26)变为

(29)

情况3把PS=ES和PR=ER/M代入到式(26)中,则式(26)改写为

(30)

情况4把PS=ES/M和PR=ER/M代入到式(26)中,则式(26)再表示为

(31)

式中

当中继端的天线数M→∞时,根据性能分析中可以看出,在情况2、情况3和情况4下,对单对和多对双向AF中继系统,其渐近可达速率都趋近一个给定常数。值得一提的是,这些定值其实是可达速率的上界,其表达式均以闭式形式给出。特别对于情况4,每个用户和中继端的发送功率都可以被缩小1/M且不会使系统性能衰减。

3 仿真分析

第2节给出了基于LoS分量的线性传输方案理论分析结果。本小节则基于这些理论结果进行仿真分析。特别地,要与文献[5]讨论的基于理想CSI(即采用全部CSI)的线性传输方案进行综合比较。

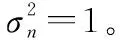
图2分别绘出了单对场景下基于LoS分量的EGC/EGT传输方案和基于理想CSI的MRC/MRT传输方案的可达速率随中继端天线数变化的曲线。图2中取PS=10 dB,PR=10 dB,ϑk=10 dB。对于采用功率缩小的情况,随着中继端天线数的增加,从图2中可以看出,其可达速率都是先增加而后逐渐趋于定值。另一方面,对于没有功率缩小情况,不论是基于LoS方案还是基于理想CSI的方案,其可达速率均一直增加。从图2中还可以看出,3种功率缩小情况下的可达速率的精确值均逐渐逼近其极限值(上界值),其中第4种情况收敛速度最快。 另外,在相同条件下,基于LoS方案的可达速率十分接近基于理想CSI方案的可达速率。

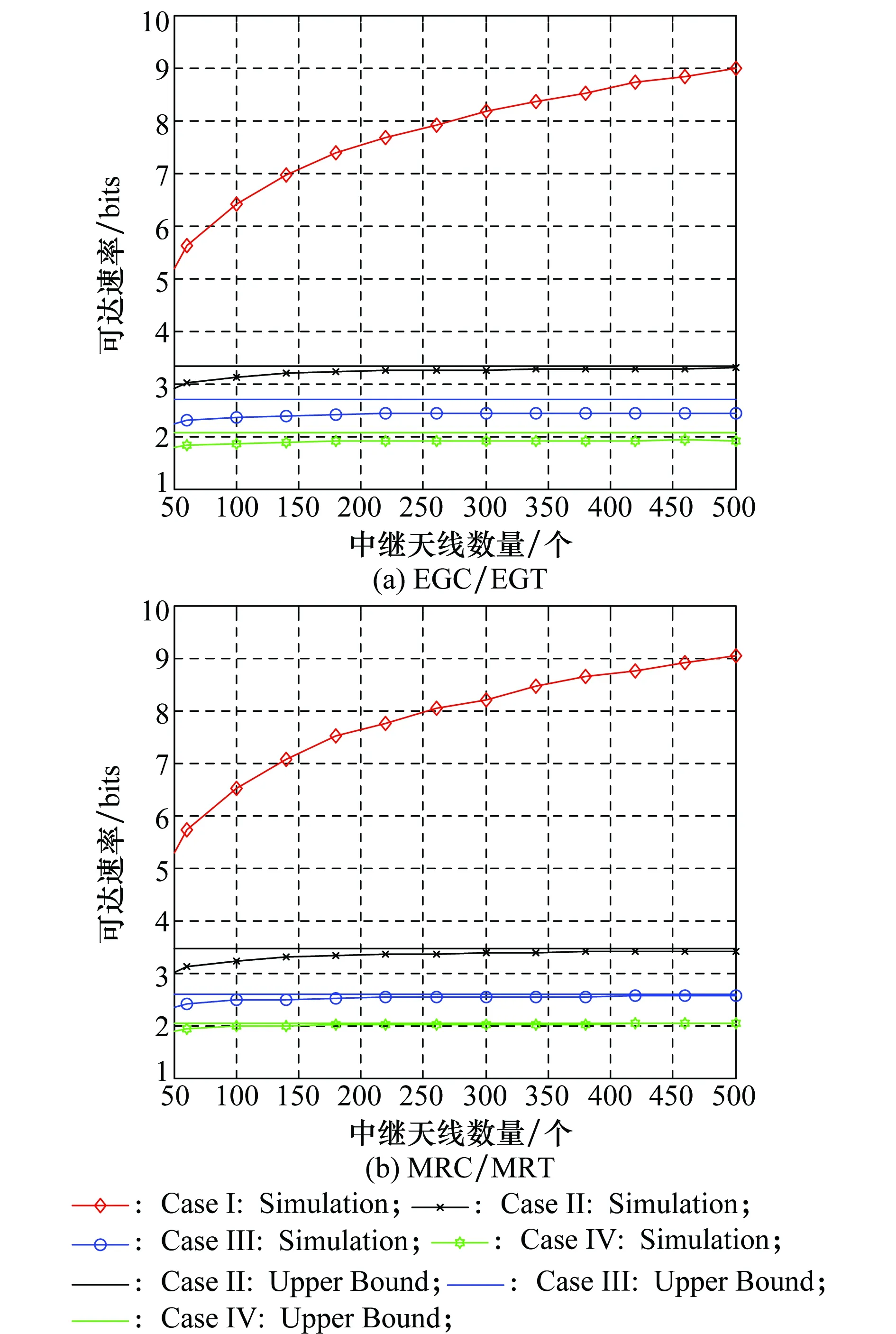
图2 单对场景4种情况下的总速率随中继端天线数变化Fig.2 Sum rate versus the number of relay antennas for the four single-pair cases

考虑情况1,并令ϑk=-5 dB,10 dB,20 dB和M=100。对于基于LoS分量的传输方案和基于理想CSI的传输方案,图3绘出了其可达速率随信噪比变化的曲线。随着SNR的增加,从图3可以发现,两个方案的可达速率都是不断增加,这与公式(20)所指出的规律是一致的。另一方面,随着ϑk的增加,在SNR>0时两种系统方案的速率都会明显提高。当ϑk≥10 dB时,基于LoS方案的可达速率相当接近基于理想CSI方案的可达速率。

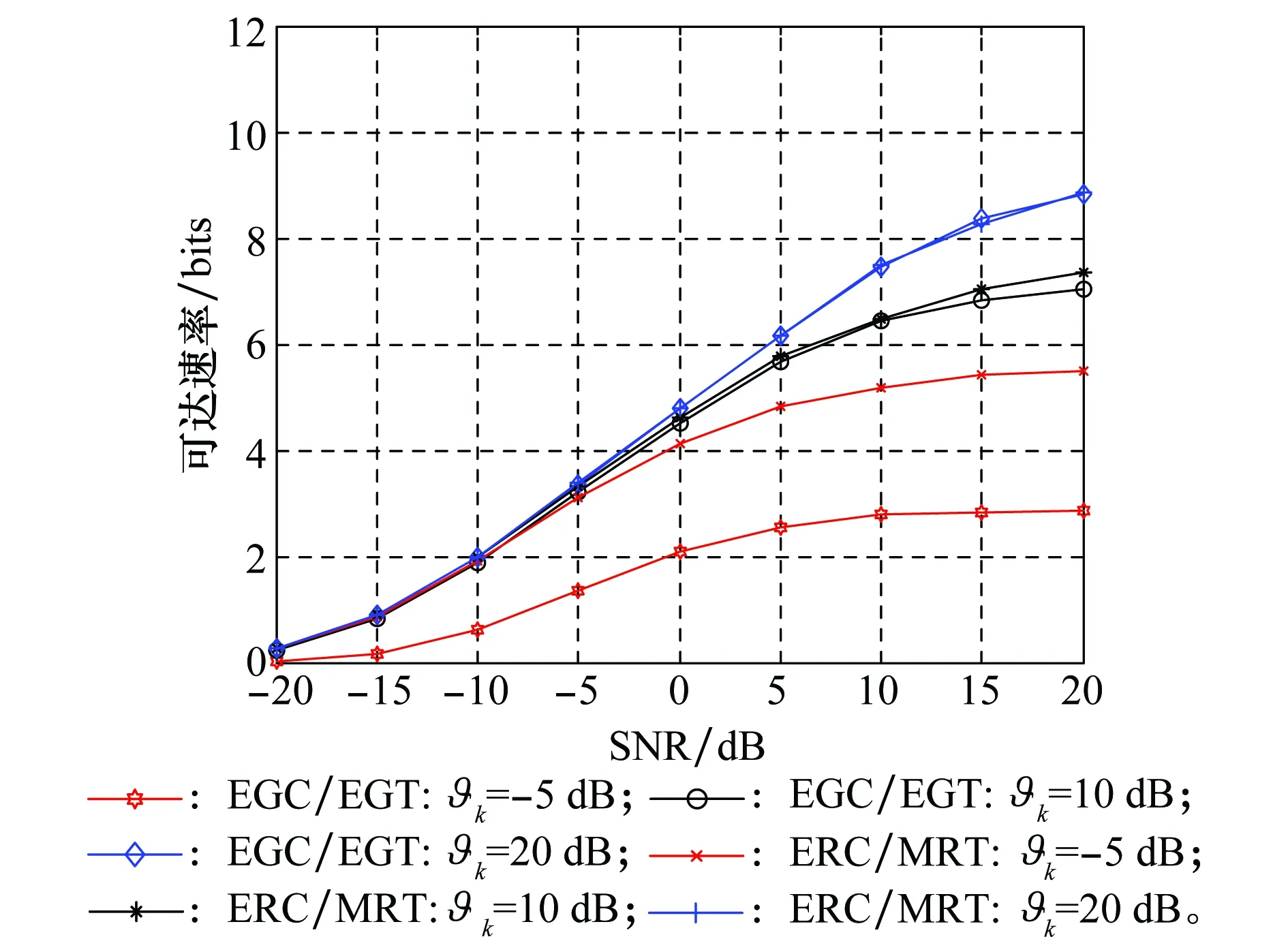
图3 随SNR变化的基于理想CSI和基于LOS线性传输方案的总速率 Fig.3 Sum rate versus SNR under the linear transmission schemes based on the perfect CSI and the LOS

图4给出了多对场景下基于LoS分量的传输方案的可达速率随中继端天线数变化的曲线。图4中设ϑk=10 dB,K=5,PS=10 dB和PR=10 dB。随着中继端天线数的增加,容易发现没有功率缩小情况下的基于LoS分量方案的可达速率可以不断增大,而3种采用功率缩小情况下的可达速率则是先增加后逐渐趋于定值,即可达速率的上界值。另外,通过对图4与图2(a) 仿真结果对比不难发现,与单对场景下情况2和情况3(或情况4)性能差相比,多对场景下情况2和情况3(或情况4)性能差则有了较大提升。

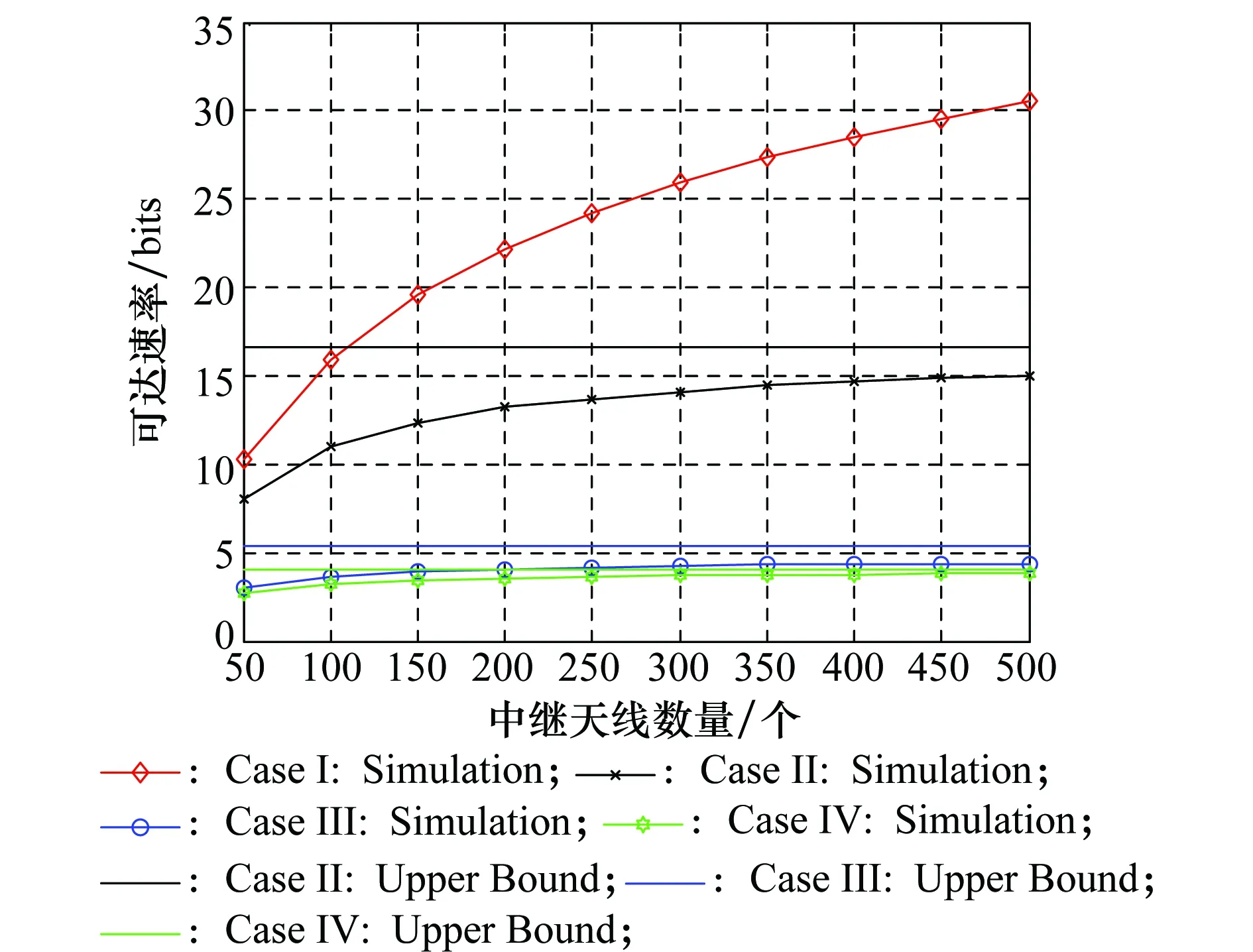
图4 多对场景4种情况下的总速率随中继端天线数变化Fig.4 Sum rate versus the number of relay antennas for the four multi-pair cases

对于基于LoS分量和基于理想CSI的传输方案,图5画出了在ϑk=10 dB时用户可达速率随用户对数变化的曲线。在图5中,将理想CSI简记为PCSI。图5(a)中,M=100,PS=10 dB和PR=10 dB。对于两种方案的总速率而言,图5中结果显示其均为K的凸函数。由凸函数性质可知,必存在使总速率达到最大的最优用户对数,图5中分别显示是15和20。随着用户对数K的增大,空间复用数目也相应增大,然而同信道干扰强度也变得越来越大,且逐渐会超过空间复用带来的增益,这样在一定的K值后可达速率的性能就会越来越变坏。在K≤15时,从图5(a)中也可以看出,基于LoS分量的方案速率与和基于理想CSI的方案的速率几乎一致,而K>15后则变得越来越差。这说明在干扰较弱情况下,EGC/EGT与MRC/MRT工作效果差不多,而在干扰较强情况下,MRC/MRT具有更高的干扰抑制能力。另一方面,从大规模MIMO系统应用考虑,如果基站天线数目达到100个左右,为了满足用户信道的正交性要求,系统选用通信用户数应在10个左右。在其他条件不变情况下,如果天线数增加到200,如图5(b)所示,最优的用户对数则分别增至为30和40，与预期的结果是一致的。图5中结果还显示,K≤30时基于LoS分量的方案速率要大于基于理想CSI的方案的速率。

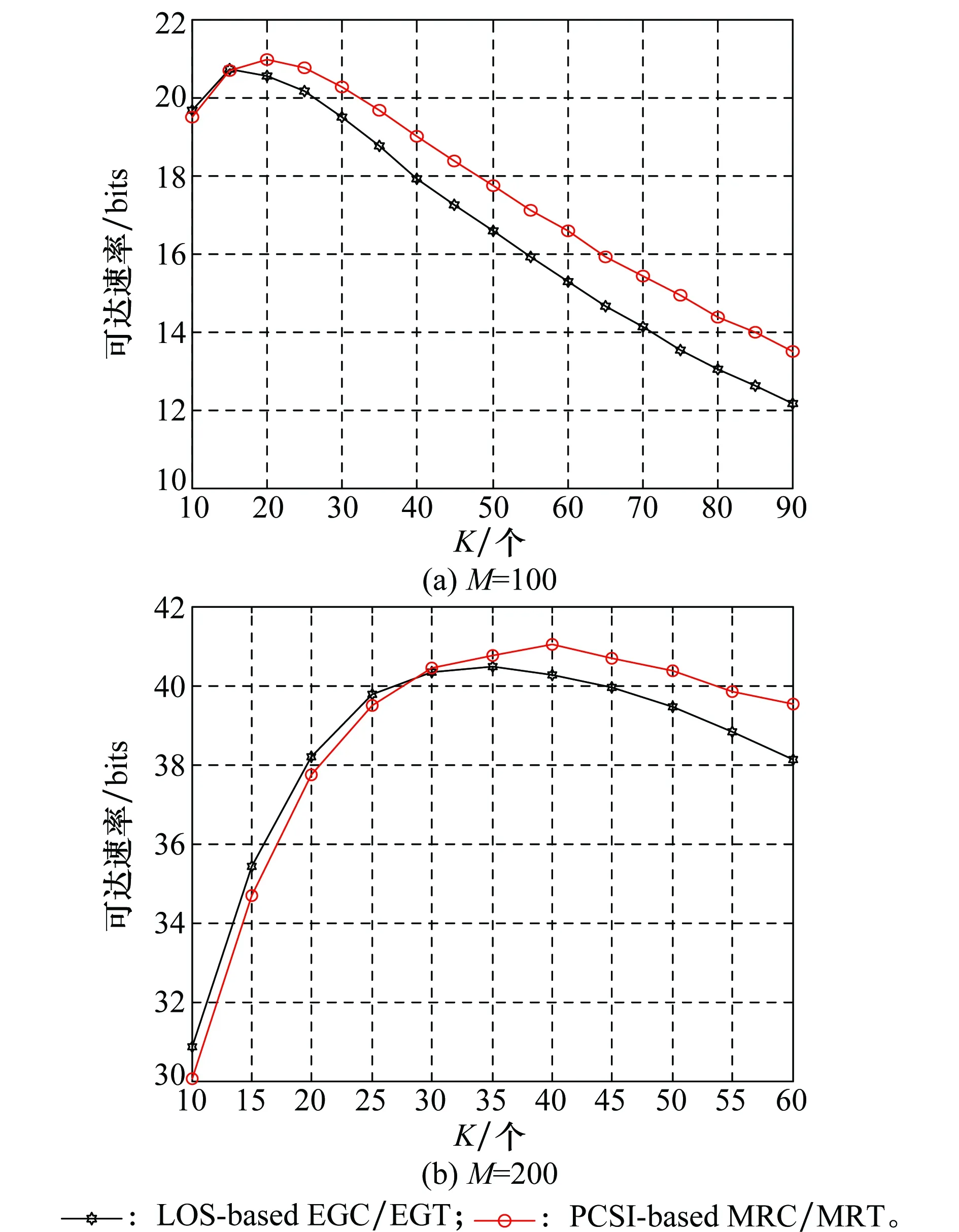
图5 随用户对数变化的基于理想CSI和基于LoS线性传输方案的总速率 Fig.5 Sum rate versus the number of users under the linear transmission schemes based on the perfect CSI and the LOS

在理想CSI情况下,除了可以采用便于分析的MRC/MRT线性传输方案,也可考虑采用复杂度较低的EGC/EGT线性传输方案。在与图5(b)相同条件下,图6给出了基于LoS和基于理想CSI下EGC/EGT方案的总速率随用户对数变化曲线。从图6可知,基于理想CSI 下EGC/EGT方案与MRC/MRT方案性能表现类似,且更加接近基于LoS的 EGC/EGT方案速率性能曲线。

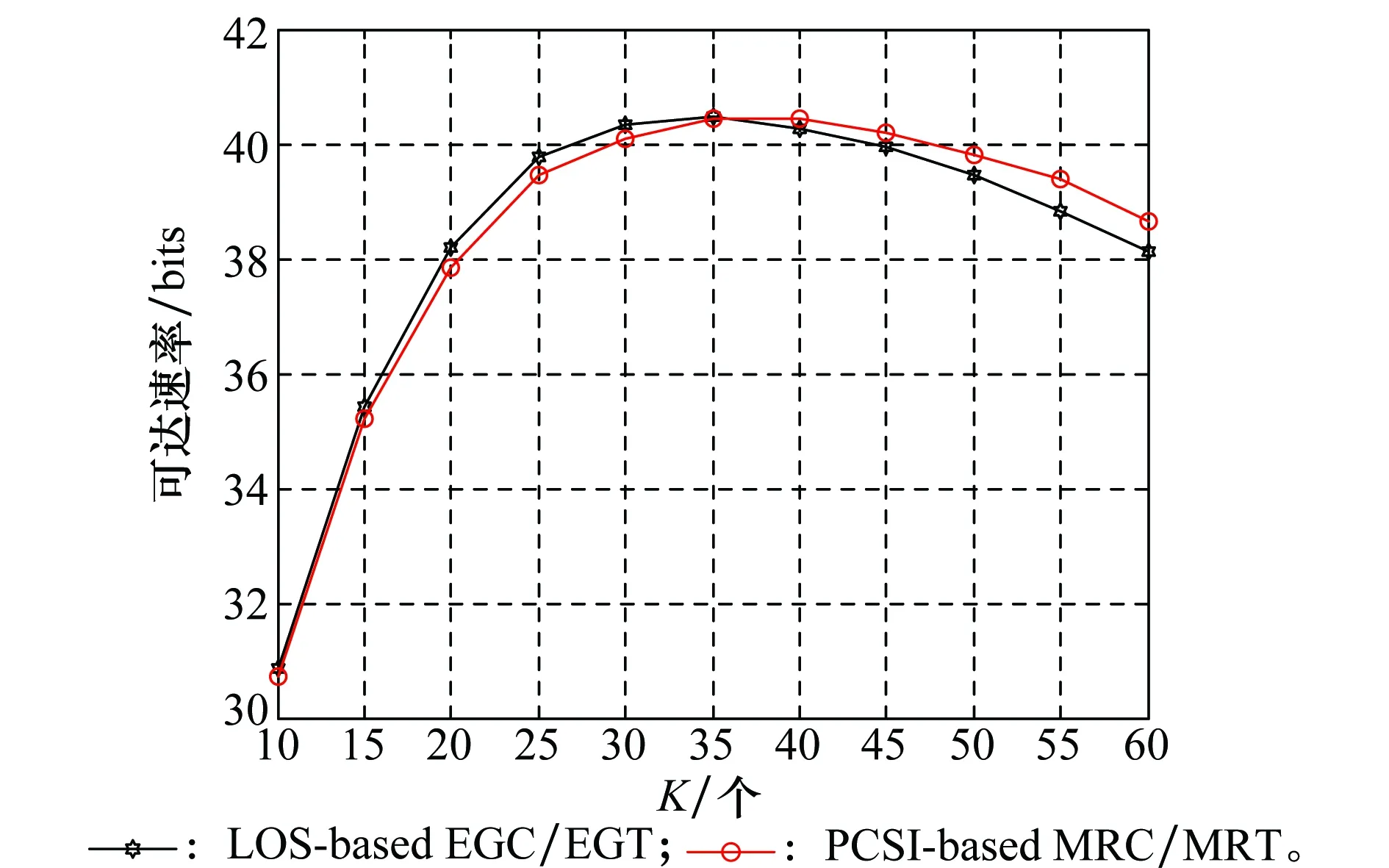
图6 随用户对数变化的基于LoS和基于理想CSI的EGC/EGT方案总速率 Fig.6 Sum rate versus the number of users under the EGC/GCT schemes based on the LOS and perfect CSI

综上仿真讨论,只要LoS分量较强,基于LoS分量的传输方案的可达速率就能很好地接近基于理想CSI 下的传输方案的可达速率。最后值得一提的是,在进行信道估计时,相比基于理想CSI 下的传输方案,基于LoS分量的传输方案将会采用相当少的时隙;因此在频谱效率方面,基于LoS分量的传输方案必然会比基于理想CSI 下的传输方案具有明显的优势。

4 结束语

中继技术是无线通信领域中值得发展的重要技术之一。对于莱斯衰落环境下的双向AF大规模MIMO中继系统,为了能有效减轻信道估计负担进而提高频谱利用率,本文提出了基于LoS分量的传输方案。该方案在中继节点采用了实现复杂度低的EGC/EGT线性放大处理。然后本文推导了该方案遍历可达速率,并对4种传输功率分配情景给出了渐近闭式表达式。仿真结果表明,在LoS分量较强的环境下,大规模MIMO中继系统更宜采用基于LoS传输方案。