冷贮备离散时间状态聚合可修系统的可靠性

温艳清, 崔利荣, 刘宝亮, 师海燕

(1. 西北工业大学机电学院, 陕西 西安 710072; 2. 北京理工大学管理与经济学院, 北京 100081; 3. 山西大同大学数学与计算机科学学院, 山西 大同 037009)

0 引 言

贮备系统的可靠性一直是可靠性领域研究的热点问题之一,对于一些高可靠性要求的产品,通过贮备部件,可以大大地提高系统的可靠性,例如航空设备、汽车零部件等[1]。研究者们在以往的可靠性研究中,常用指数分布作为故障时间的分布。指数分布具有无记忆性且解析式易于处理,但其只适应于寿命具备无记忆的设备场合,对于寿命是退化型的设备(部件),再用指数分布去刻画效果就不太理想。为了克服以上困难,假设所涉及的分布是一般分布时,通过运用补充变量法可以处理相对比较简单的可用度模型,对于比较复杂的模型,这些方法显得举步维艰。位相型(phase-type, PH)分布可以把任一个非负连续随机变量逼近到任意的精度,且任何取值为正整数的离散概率分布是一个离散PH分布[2]。由于PH分布具有指数分布易处理的特点,所以其在排队论、交通系统、统计信号处理、可靠性理论[3-7]等方面取得了广泛应用。以上参考文献都是针对连续时间情形下系统模型的,然而实际工程领域中,并不是所有的系统都能被连续地检测,正如国际著名可靠性专家Ruiz-Castro[8]所说:“或许因为不可能进行连续的检测,或许因为系统自身内部结构的原因,工程上一些系统仅仅能在某些离散时间点被检测,例如土木和航空工程领域的设备。”近年来,离散时间情形下系统可靠性的研究越来越得到学者们的重视。文献[8-11]在假设系统模型中所涉及的时间分布均为离散PH分布的情形下，研究了各种离散时间系统模型的可靠性。修理工多重休假策略在连续时间系统可靠性建模[12-15]中被研究者们广泛使用,因为这样使修理工这个人力资源得到更有效的利用。在连续时间情形下,文献[5]假设所涉及的随机时间分布为连续PH分布,研究了修理工具有多重休假的两部件可修系统的可靠性;文献[7]假设所涉及的随机时间分布为连续PH分布,考虑了修理工带多重休假的n部件冷贮备系统的可靠性。修理工多重休假是指当系统中的部件都完好时,修理工离开系统去休假,休假结束返回系统中,如果发现系统中有故障部件等待修理,那么他开始修理故障部件,直到系统中没有故障部件,他再离开系统去休假。这儿的“休假”指的是修理工兼职去做一些其他的事情,使得修理工这个人力资源得到充分的利用。例如:铁路维修工对火车、地铁等的维修检查,不同工作的时间分配,船舶修理工的救助待命就属于多重休假,有紧急救助时工作,没有救助就做别的维修检测。到目前为止,所了解的文献中,尚没有学者在所涉及到的随机分布为离散PH分布的假设下研究有多重休假的贮备系统,因此本文研究离散时间下修理工可多重休假的冷贮备系统的可靠性,系统中有2个部件,一个部件正常工作,另一个部件冷贮备,工作部件出现故障,冷贮备部件立即替换变为工作部件。部件正常工作时间、修理时间、修理工的休假时间都服从离散时间的PH分布。本文所建的模型在工程实践中有广泛的应用,例如医生在进行大型手术的时候,有两个供电系统:正常电力供应系统(可以看作部件1)和应急发电系统(可以看作部件2,作冷贮备),电力系统维护工(修理工)可以进行多重休假。又如可以把飞机上的两个同样的发动机看作两个部件,当其中一个发动机正常运转的时候,飞机将正常工作,供电系统扮演修理工的作用,其将给飞机的每个子系统进行正常电力供应,即进行休假。当正运转的这个发动机故障停止运转时,另一个发动机立即启动,同时这个“修理工”也将给检测和维护系统供电来检测和维护出现故障的这个发动机。本文所建立的模型是文献[5]中模型在离散情形下的推广,在工程实践中,系统只在离散时间检测普遍存在,例如火车、飞机、船舶上的一些关键零部件的检测。由于任何取值为正整数的离散概率分布是一个离散PH分布,且离散时间情形并不是连续时间情形的一个特殊情况,当系统在离散时间情形下运行,在线部件的故障、修理的完成以及休假的完成能够同时发生,这是与连续时间情形下完全不同的,所以本文所得结果更具有一般性,有重要的理论和实际应用价值,可以为管理人员的管理决策提供依据。

下面介绍Kronecker积与Kronecker和的定义,其在随后论文的研究中被大量使用。

定义1[16]Kronecker积

如果A和B分别为m1×m2和n1×n2的矩阵,则其Kronecker积A⊗B是阶数为m1n1×m2n2的矩阵,且

定义2[16]Kronecker和

如果A和B分别为m和n阶方阵,则Kronecker和定义为

A⊕B=A⊗In+Im⊗B

式中,In和Im分别为m和n阶单位矩阵。

1 系统模型建立

考虑修理工具有多重休假的冷贮备离散时间可修系统,系统由2个部件和1个修理工组成,系统模型的假设如下:

(1)κ=0时刻,部件都是新的。系统一旦启动,其中一个部件开始工作,另一个部件冷贮备,修理工立即进入休假,在休假结束后,两个部件仍没有出现故障,重新开始另一次休假,称为多重休假;若工作部件发生故障需要维修,冷贮备部件(如果系统中有贮备部件)立即替换这个故障部件开始工作。

(2) 修理工的多重休假策略参考文献[6]中系统模型建立中的(2)。

(3) 部件正常工作时间X, 修理时间Y, 修理工的休假时间Z相互独立,都服从离散的PH分布,且X～PH(α,T),位相的阶数为m,Y～PH(β,S),位相的阶数为k,Z～PH(γ,L)。假设随机变量X,Y,Z相互独立。

基于以上的假设,系统可以用一个离散时间Markov链{Xn,n=0,1,2,…}来描述,其状态空间是S={S1,S2,S3,S4,S5},其中，S1,S2,S3,S4,S5是宏状态,下面给出这些宏状态表示的具体意义。

S1={(0,i,l),1≤i≤m,1≤l≤k}表示一个部件正常工作,工作时间在位相i,另一个部件冷贮备,修理工处于休假状态,且修理工休假在位相l。

S2={(1,i,l),1≤i≤m,1≤l≤k}表示一个部件正常工作,工作时间在位相i,另一个部件出现故障,修理工处于休假状态,休假时间在位相l。

S3={(1,i,j),1≤i≤m,1≤j≤n}表示一个部件正常工作,工作时间在位相i,另一个部件出现故障,修理工正在修理故障部件,修理时间在位相j。

S4={(2,l),1≤l≤k}表示两个部件都发生故障,修理工在休假,休假时间在位相l。

S5={(2,j),1≤j≤n}表示系统中两个部件都发生故障,修理工在修理第一个故障的部件,修理时间在位相j,另一个部件等待修理。

在上述假设下,系统的状态空间为S=W∪F={S1,S2,S3}∪{S4,S5},其中,W表示系统的工作状态集;F表示系统的故障状态集。系统的转移概率矩阵表示为P,其是一个分块矩阵,每一块相应于S={S1,S2,S3,S4,S5}中状态之间的转移,即

S1S2S3S4S5

(1)

下面说明转移概率矩阵矩阵P中的这些分块元素如何得到。

转移S1→S1相应于T⊗L+T⊗L0γ。这是两项的和,因为系统中没有发生部件故障修理工休假也没有结束,表示为T⊗L;或者修理工休假结束了但发现系统中没有故障部件,所以其进行第二次休假,表示为T⊗L0γ。

转移S1→S2相应于T0α⊗L。这是因为正常工作的部件出现故障,冷贮备部件立刻取代其开始工作,表示为T0α,而修理工仍然在休假L。

转移S1→S3相应于T0α⊗L0⊗β。这是由于正常工作的部件出现故障,冷贮备部件取代其工作,表示为T0α,修理工休假结束后发现有故障部件,立即开始修理,表示为β。

转移S2→S2相应于T⊗L。这是因为系统中在线工作的部件没有发生故障T,修理工的休假也没有结束L,所以先前故障的部件也没有得到修理。

转移S2→S3相应于T⊗L0⊗β。这是因为在线工作的部件没有发生故障T,修理工从休假返回，发现系统中有一个故障部件等候修理L0,所以其立即以初始向量β开始修理这个故障部件。

转移S2→S4相应于T0⊗L。这是因为系统中在线工作的部件发生了故障T0,而修理工仍然在休假L,先前故障的部件也没有得到修理。

转移S2→S5相应于T0⊗L0⊗β。这是因为系统中在线工作的部件发生了故障T0,修理工从休假返回L0,立即开始修理第一个故障部件β。

转移S3→S1相应于T⊗S0⊗γ。这是因为修理工正在修理的故障部件修理完好了S0,而在线工作的部件没有发生故障T,所以其以初始向量γ开始休假。

转移S3→S3相应于T⊗S+T0α⊗S0β。这是两项的和,因为系统中在线工作的部件没有发生故障且正在修理的故障部件也没有修理完成,表示为T⊗S;或者正在修理的故障部件修理完好了且在线工作的部件发生了故障,所以这个刚修理完好的部件代替其开始工作,修理工继续修理这个刚发生故障的部件,表示为T0α⊗S0β。

转移S3→S5相应于T0⊗S。这是因为在线工作的部件发生了故障T0,而正在修理的故障没有修理完成S,所以其只能排队等待修理。

转移S4→S4相应于L。这是因为修理工仍然在休假L,所以两个故障的部件继续等待修理。

转移S4→S5相应于L0⊗β。这是因为修理工从休假返回L0,所以其立即以初始向量β修理先发生故障的部件,另一个部件等待修理。

转移S5→S3相应于α⊗S0β。这是因为正在修理的部件修理完成了S0,所以这个部件立即以初始向量α在线开始工作,修理工继续以初始向量β开始修理另一个故障部件。

转移S5→S5相应于S。这是因为正在修理的部件没有修理完成。

2 系统的可靠性指标

2.1 稳态概率向量

用向量π=(π1,π2,π3,π4,π5)表示相应于转移概率矩阵P的稳态概率向量,则这个稳态向量满足矩阵方程πP=π且πe=1,即

(2)

通过运用计算程序可以得到这个方程组的解,以下假定稳态概率向量π1,π2,π3,π4,π5是已知的。

2.2 可用度

系统的可用度定义为:在时刻κ,系统正常工作的概率,也就是说两个部件中少有一个部件是正常工作的。令系统在宏状态{S1,S2,S3,S4,S5}之间的转移概率矩阵记为P,所以在时刻κ,系统的可用度为

(3)

⊗γ,0)Pκ]1∶mk,

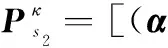
(α⊗γ,0)表示系统的初始状态概率,即初始时刻系统中两个部件都是完好的,处于宏状态S1。

在式(3)中让κ→∞取极限,可得系统的稳态可用度为

A=π1e+π2e+π3e=1-π4e-π5e

(4)

2.3 故障的条件概率

故障的条件概率包括在线部件故障的条件概率和系统故障的条件概率。当系统处于宏状态S1,S2或者S3时,在线部件或许发生故障;系统中两个部件都不能正常工作了，系统就发生了故障,所以只有当系统处于宏状态S2或者S3时,系统才可能发生故障,因此在时刻κ,在线部件故障的条件概率为

(5)

稳态时在线部件故障的条件概率为

v=π1(T0⊗e)+π2(T0⊗e)+π3(T0⊗e)

(6)

时刻κ系统故障的条件概率为

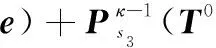
(7)

稳态时系统故障的条件概率为

vs=π2(T0⊗e)+π3(T0⊗e)

(8)

可见,在线部件故障的条件概率大于系统故障的条件概率。

2.4 可靠度

S1S2S3S*

(9)

式中,S*是吸收状态。令矩阵U是矩阵P*去掉最后一行和最后一列所得到的矩阵,则系统的可靠度为

R(κ)=(α⊗γ,0)Uκe

(10)

系统首次故障前的平均时间为

MTTFF=(α⊗γ,0)(I-U)-1e

(11)

3 数值算例

以某供电系统为例,该供电系统由正常电力供应系统、应急发电系统和电力系统维护工(修理工)组成。下面对其进一步假设与描述。

正常电力供应系统的工作时间X～PH(α,T),且

X的均值为220。

故障供电系统的修理时间Y～PH(β,S):

Y的均值为10。

电力系统维护工的休假时间Z～PH(γ,L):

Z的均值为20。

运用Matlab软件,可以求得供电系统的稳态概率向量为

π1=(0.421 1,0.369 4,0.044 8,0.039 4)

π2=(0.037 7,0.035 4,0.001 8,0.001 7)

π3=(0.020 1,0.019 6,0.001 2,0.001 3)

π4=(0.001 7,0.001 6)

π5=(0.001 3,0.001 6)

图1是供电系统的可用度曲线,可以看出,在时刻κ=170之后,供电系统达到稳定状态,且供电系统达到稳态时,在工作状态集W中逗留的概率为0.993 8,即供电系统大约有99.38%的时间是可用的。图2是供电系统的可靠度曲线,可以求得供电系统首次故障前的平均时间为MTTFF=3 449.6。图3和图4分别是在线运行供电设备和供电系统的故障条件概率曲线,可以看出,两条曲线在刚开始的一段时间内快速上升,在时刻κ=80之后,系统在线部件故障的条件概率达到稳定值,且为0.004 5;而在时刻κ=210之后,系统故障的条件概率达到稳定值,为3.043 2×10-4。在相同的时刻点,在线部件故障的条件概率值要远远大于系统故障的条件概率值,这与直觉是相吻合的。

图1 系统的可用度曲线Fig.1 Curve of the system availability

图2 系统的可靠度曲线Fig.2 Curve of the system reliability

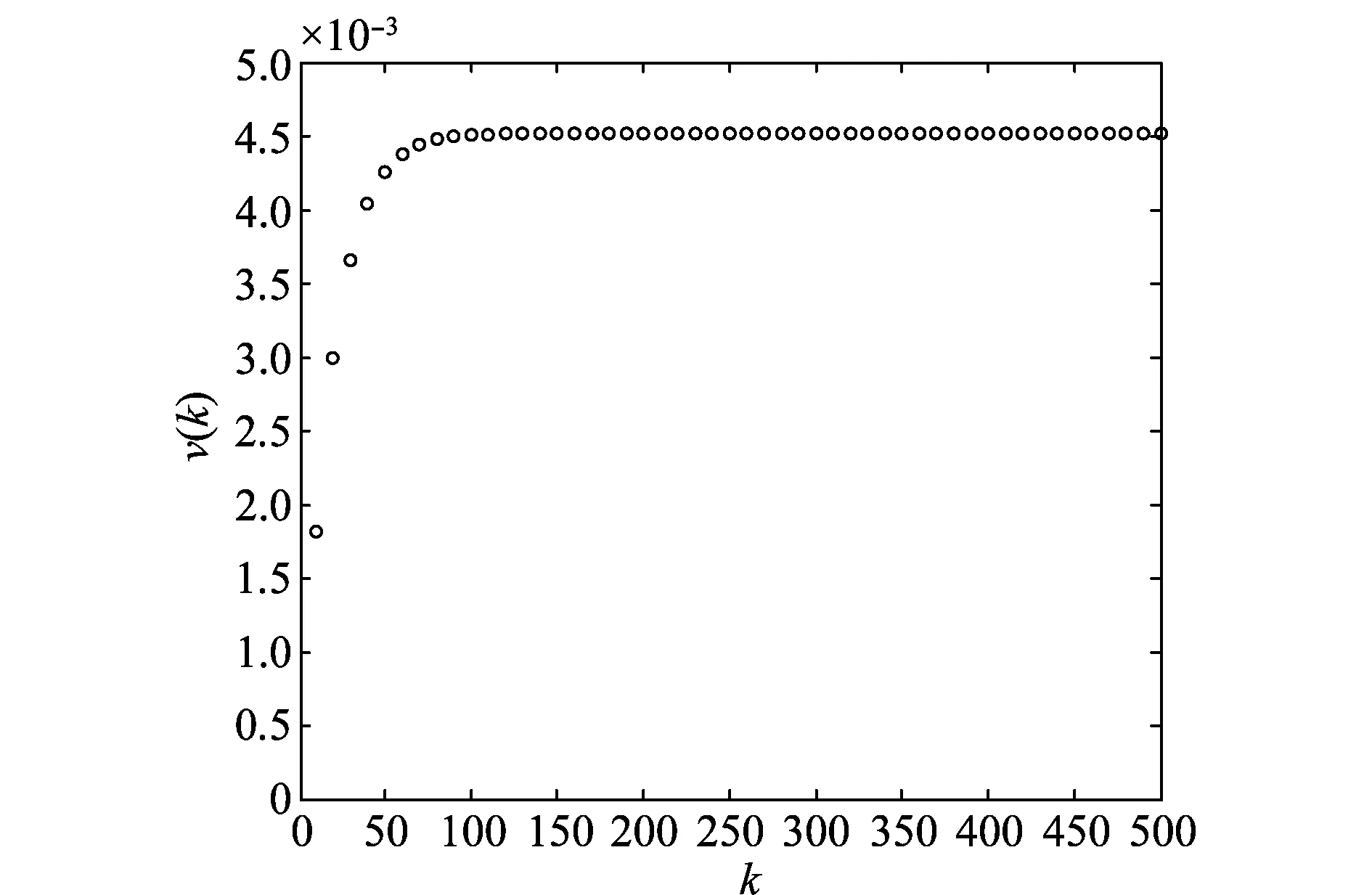
图3 在线部件故障的条件概率曲线Fig.3 Conditional probability of failure for the online component

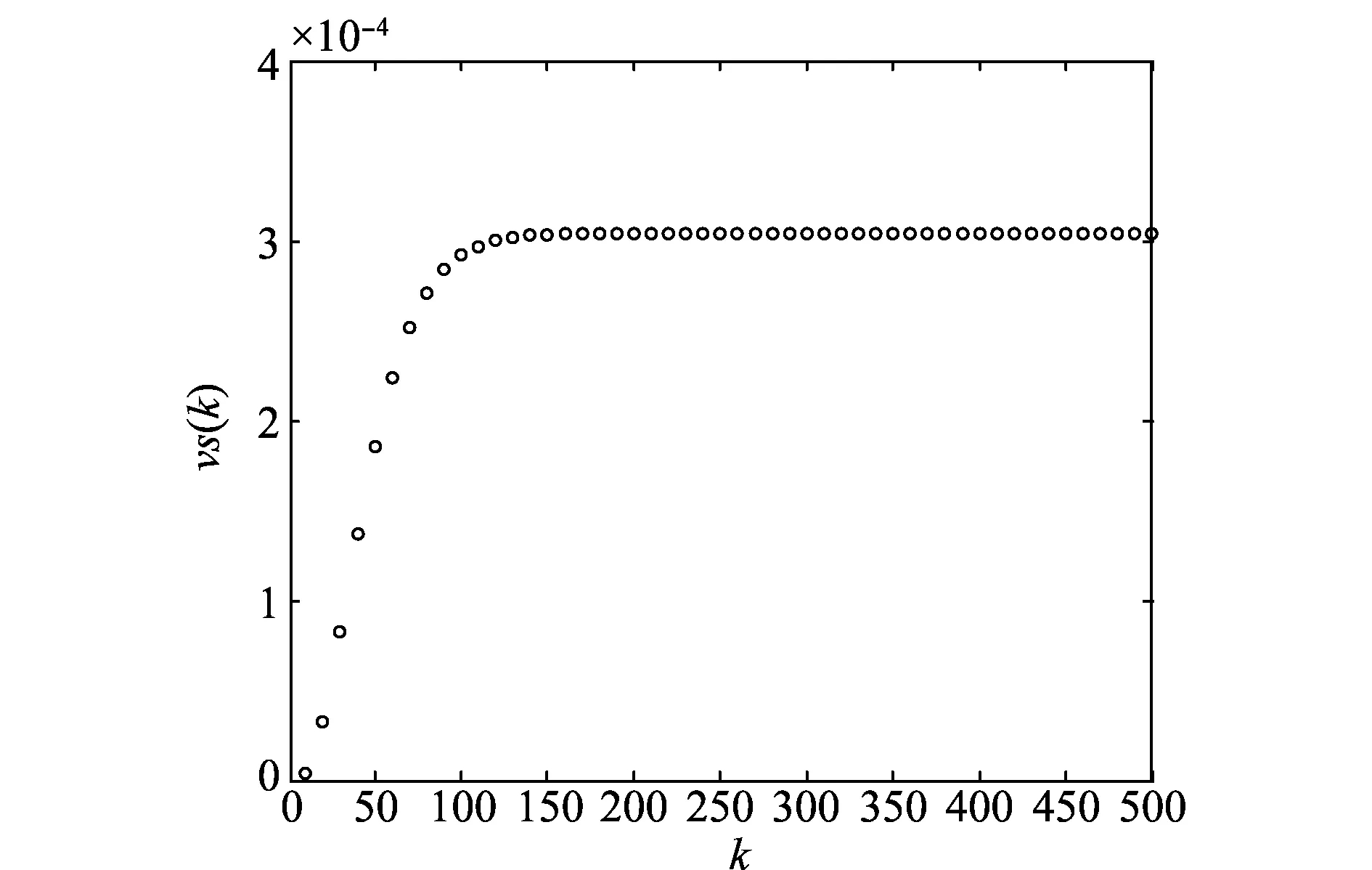
图4 系统故障的条件概率曲线Fig.4 Conditional probability of failure for the system

4 结 论

(1) 把修理工的多重休假策略加入到离散时间可靠性模型的建模中,建立了修理工具有多重休假的两部件冷贮备离散时间系统模型。

(2) 假设所涉及的随机分布均为离散PH分布,且任何取值为正整数的离散概率分布是一个离散PH分布,所以建立的离散时间可靠性模型更具有一般性。

(3) 推导出离散时间可靠性系统所特有的可靠性指标:故障的条件概率以及可靠性系统模型一些常见的可靠性指标(可用度和可靠度)。

(4) 本文仅研究了离散时间情形下一种只有2个部件的特殊的系统模型,如果将其推广到更一般的系统模型,如部件数增加、部件故障机理复杂化(遭受冲击)、维修策略多样化等,系统在离散时间情形下运行,在线部件的故障、修理的完成以及休假的完成能够同时发生,系统状态和维数将急剧增加,推导系统的转移率矩阵考虑的情形将非常复杂,这是后续将要研究的一些问题。