海上多舰协同防空部署优化研究

杨 毅, 南 英

(南京航空航天大学航天学院, 江苏 南京 210016)

0 引 言

海上多舰协同防空部署,是合理有效地利用多个舰艇的防空区域和拦截能力,对其所处的位置和舰艇朝向角度做出规划,使其能够最大程度上应对敌方来袭导弹群体的攻击,保护我方受保护目标(航母、岛屿等)的安全。海上多舰协同航空部署优化是一个复杂,多约束的优化问题,其设计到地方反舰导弹的性能参数,来袭数目和我方防御实力,包括拦截区域,火力通道等多个参数。

对空防御是现代战争中必不可少的研究领域,由其衍生的研究方向包括拦截策略结构[1],目标分配[2-4],以及多舰部署[5-6]等。多舰协同防空部署问题本质上是一个优化问题,通过优化各掩护舰的位置和朝向,使得多舰对来袭目标的拦截性能指标最高。赵建印, 刘芳[5]在武器系统既定的情况下,以防御纵深最大为优化指标,给出了双舰部署优化模型和求解算法,该方法使用防御纵深作为部署优化的性能指标,很大程度上简化了优化的难度,但是该方法仅能优于双舰防空部署优化,并且文章中假定舰艇防空区域内的拦截概率相同仍有待商榷。

多舰协同防空部署主要应对地方反舰导弹对我方主舰的打击。目前,对于反舰导弹的研究可以分为低空掠海导弹[6-9]和高空巡航导弹[10], 低空反舰导弹主要利用地球曲面来躲避雷达扫描,高空反舰导弹通过高空灌顶攻击实现突防,文献[11]采用模糊集合理论构建了反舰导弹的威胁度模型,考虑了导弹距离、相对速度、导弹夹角、舷角等因素的关系。不同飞行高度会采用不同的机动方式来实现突防。对应不同的反舰导弹,舰空导弹的拦截概率和杀伤范围也不相同,所以舰协同防空部署问题首先要构建舰艇对来袭目标的拦截模型,文献[12]通过设计护卫舰队来袭目标单元的拦截概率,推导建立了被掩护舰的生存概率模型,并提供了该模型下的编队队形最佳配置的计算方法。该方法仅考虑了单个来袭目标的情况,并且被掩护舰的生存概率取决于我方兵力的使用方式;文献[13]给出了多舰协同防空中的水平杀伤区计算方法,文献[14-15]在防空部署优化问题中给出了三维的防空杀伤区模型的计算方法,并给出各舰艇的最早发射时间仿真。文献[16]给出了多舰协防的协同通信网络优化,实现多区域多集群多区域的协同通信和防空。文献[17]从电子对抗、火力协同、指挥通信和区域掩护四个方面综合地对拦截舰编队防空进行了论述和分析,并构建了舰队防空队形的数学模型。文献[18]基于神经网络给出了计算杀伤区边界的计算方法。以上的杀伤区计算都没有考虑在目标强机动情况下[19-20],在目标采用突防机动过程,拦截导弹的拦截区会发生改变。在某个区域内,突防目标无论采取任何机动,拦截导弹都能拦截突防目标,则该区域为不可逃逸区[20-22]。

为了提高我方掩护舰对来袭目标的拦截概率,降低敌方导弹对受保护目标的威胁程度,海上多舰协同防空部署需要优化各掩护舰的位置坐标和舷角朝向,使得综合拦截性能指标最小。本文综合考虑导弹群体的数量和飞行状态和掩护舰的性能参数,构建合理准确的防御部署性能指标,引入了掩护舰的可拦截区内对来袭目标的威胁度建模,将来袭目标在可拦截区内飞行过程中收到的威胁度积分和作为防御部署性能指标的重要组成部分,结合来袭目标的参数以及掩护舰的火力通道、拦截概率等参数,设计了多舰协同拦截来袭导弹群体的威胁度模型。

目前已经有大量的优化算法应用于在多目标防空优化问题上,较为常见的智能算法有遗传算法(particle swarm optimization, PSO)[23]、粒子群算法[24-25]、以及其他算法[26-27]。本文在所设计的威胁度模型下,采用共生有机搜索(symbiosis organisms search, SOS)算法对其部署方案进行了优化。SOS算法[28]是一种通过模拟共生、共栖和寄生3种生物间的生存关系对目标问题进行不断迭代优化的算法,该算法在许多工程领域上都取得了很好的应用[29-32]。最后的仿真分析结果表明该算法能够快速收敛到最优解,相较于PSO算法收敛速度提高近10%,不会陷入局部最优,所求得的最优防空部署方案能够有效针对来袭导弹群体中威胁较强的群体,使其进攻弹道上威胁度最高。

1 问题描述

海上多舰协同防空部署优化问题是针对可探测或可预估的来袭导弹群体,根据我方掩护舰的弹量配给和拦截能力,优化部署各掩护舰的位置和朝向角,使得我方掩护舰对敌方目标的总体拦截概率最高。

我方受保护目标为原点(0,0),已经探测得知敌方来袭导弹共有NT个群体从不同的方向向受保护目标进攻,各导弹群体Ti(i=1,…,NT)根据其导弹特性的不同,假设其分别对应各群体Ti的导弹类型为Tti,该类型导弹的评价飞行速度为Tvi,群体内含导弹数量为Tmi。我方共具备NC个掩护舰,各掩护舰Cj(j=1,2,…,NC),各掩护舰所能携带的拦截弹种类固定,所携带的弹量对应Cj为Cnj。海上多舰协同防空部署优化问题要求优化各掩护舰的部署位置坐标(xj,yj)及舰船舷角θj,使得在该拦截部署条件下,使得以下性能指标最小:

i=1,2,…,NT;j=1,2,…,NC

(1)

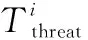
海上多舰协同防空部署优化问题需要满足一下约束条件。

我方单位各掩护舰(包括被保护目标)之间距离必须不小于安全距离rmin:

(2)

我方各掩护舰距离受保护目标距离不得超过最大范围rmax:

(3)

1.1 来袭导弹威胁度建模

鉴于假设所有来袭导弹群体的攻击目标均为我方受保护目标,所以在构建来袭导弹的威胁度模型时,不需要考虑来袭导弹的偏航角因素。本文中来袭导弹的威胁度主要取决于其距离受保护目标的距离、导弹速度、导弹数量。来袭导弹群体Ti的威胁度为

(4)

式中,Tmi为导弹群体Ti的导弹数目;Vi为导弹群体Ti的飞行速度;Di为导弹群体Ti距离受保护目标的距离。导弹群体Ti对我方受保护目标的威胁度与导弹数量以及到达时间成正比。

1.2 掩护舰威胁度建模

在敌方导弹突防进攻受保护目标的过程中,我方掩护舰会在其飞行弹道上对其进行协同拦截,我方掩护舰对敌方导弹群体的威胁度与以下因素相关:

(1) 我方掩护舰携带导弹类型对敌方导弹类型的拦截概率pij

我方具有的拦截导弹类型Ctj(j=1,2,…,MC),对应敌方导弹所有类型Tti(i=1,2,…,NT)的拦截概率表如表1所示。

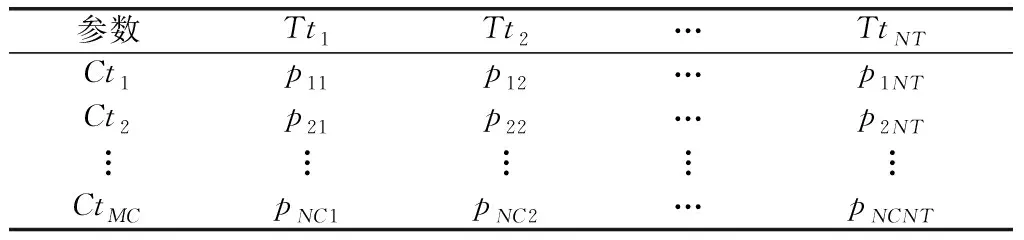
表1 掩护舰拦截弹拦截概率表

(2) 我方掩护舰火力通道数fnj

掩护舰的火力通道数表明该掩护舰可以在同一时间发射fnj枚拦截导弹进行拦截,掩护舰的火力通道数越大,表明该拦截舰的拦截威胁越高。

(3) 敌方导弹经过我方掩护舰可拦截区域的距离长度lij

敌方导弹突防通过我方掩护舰可拦截区的距离或时间越长,掩护舰对敌方导弹的可拦截的机会越多,威胁越大。掩护舰的可拦截区范围由以下参数确定:可拦截区远边界,可拦截区近边界,最大高低角,最大射高,最小射高,最大扇面角,最大航路捷径。

掩护舰可拦截区示意图如图1和图2所示,其中图1是可拦截区的垂直面投影,图2是可拦截区的水平面投影。在目标不机动的情况下,舰空导弹可以在可拦截区有效拦截目标,在目标存在任何机动的情况,仍能对目标有效拦截的区域成为不可逃逸区[21],即图2中的红色虚线。

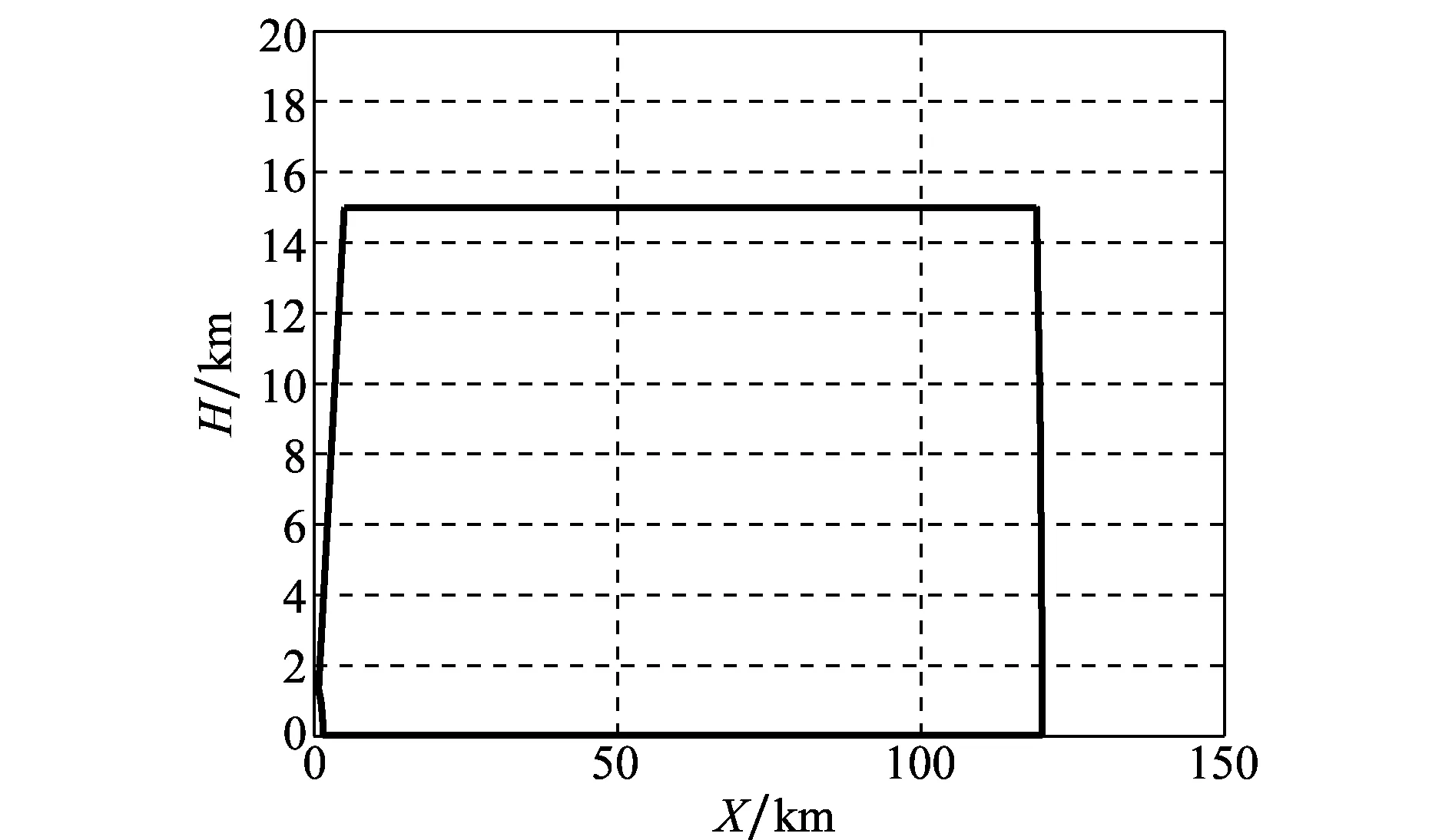
图1 掩护舰可拦截区示意图垂直投影Fig.1 Intercept zone of warship on vertical plane

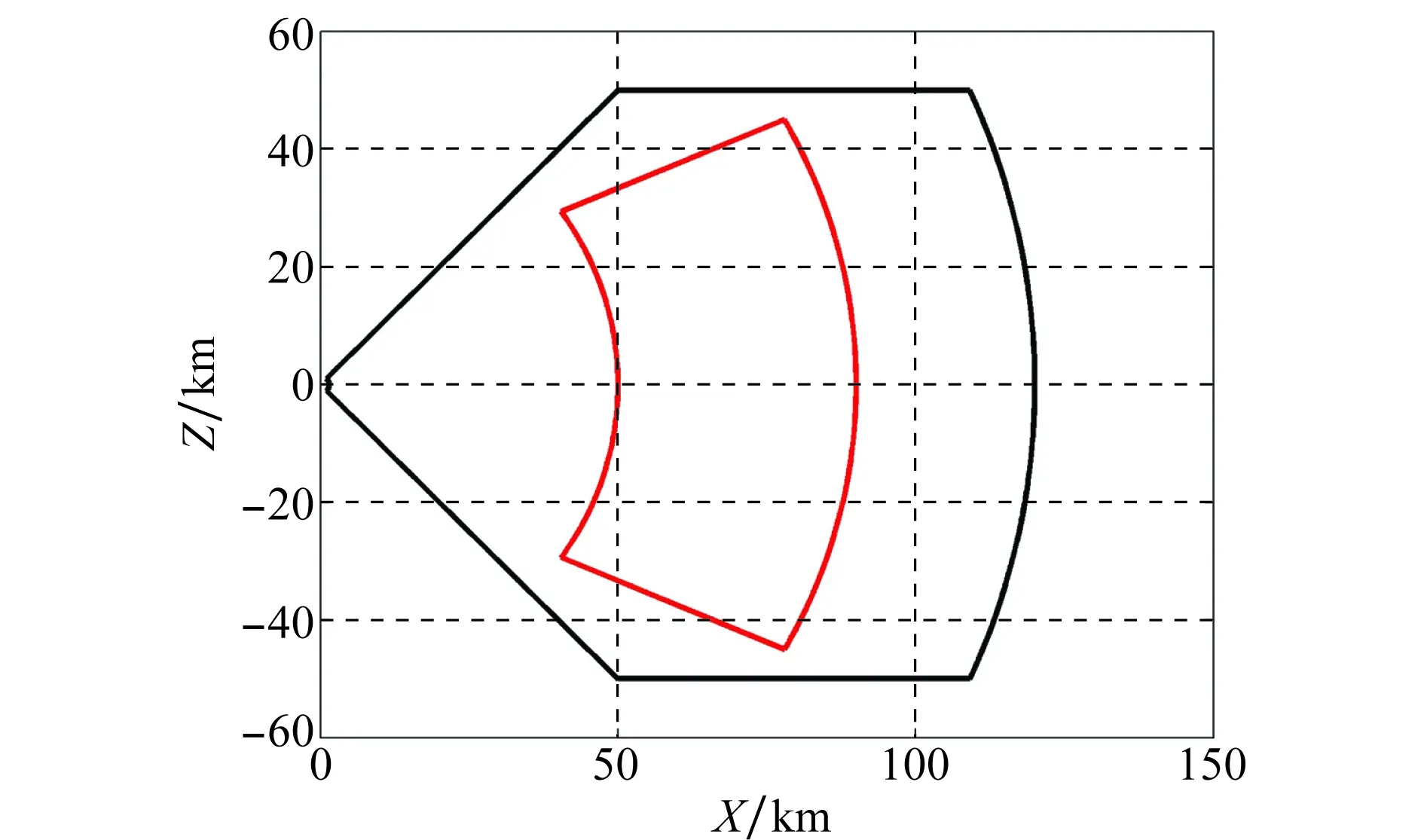
图2 掩护舰可拦截区示意图水平投影Fig.2 Intercept zone of warship on horizontal plane

针对掩护舰的可拦截区随高度变化的特性以及不可逃逸区的位置,本文设计了掩护舰的可拦截区内的威胁度分布函数越靠近可拦截区的中心区域,威胁度越大。若导弹处于可拦截区的不可逃逸区内,则威胁度为1,不可逃逸区外到可拦截区边界之间的区域,威胁度从1逐渐减少至0。根据不可逃逸区的特性,本文采用钟形函数构建了图1可拦截区的威胁度分布函数,钟形函数表达式如式(5)所示,可拦截区威胁度分别随拦截距离和发射偏航角的关系如图3和图4所示。

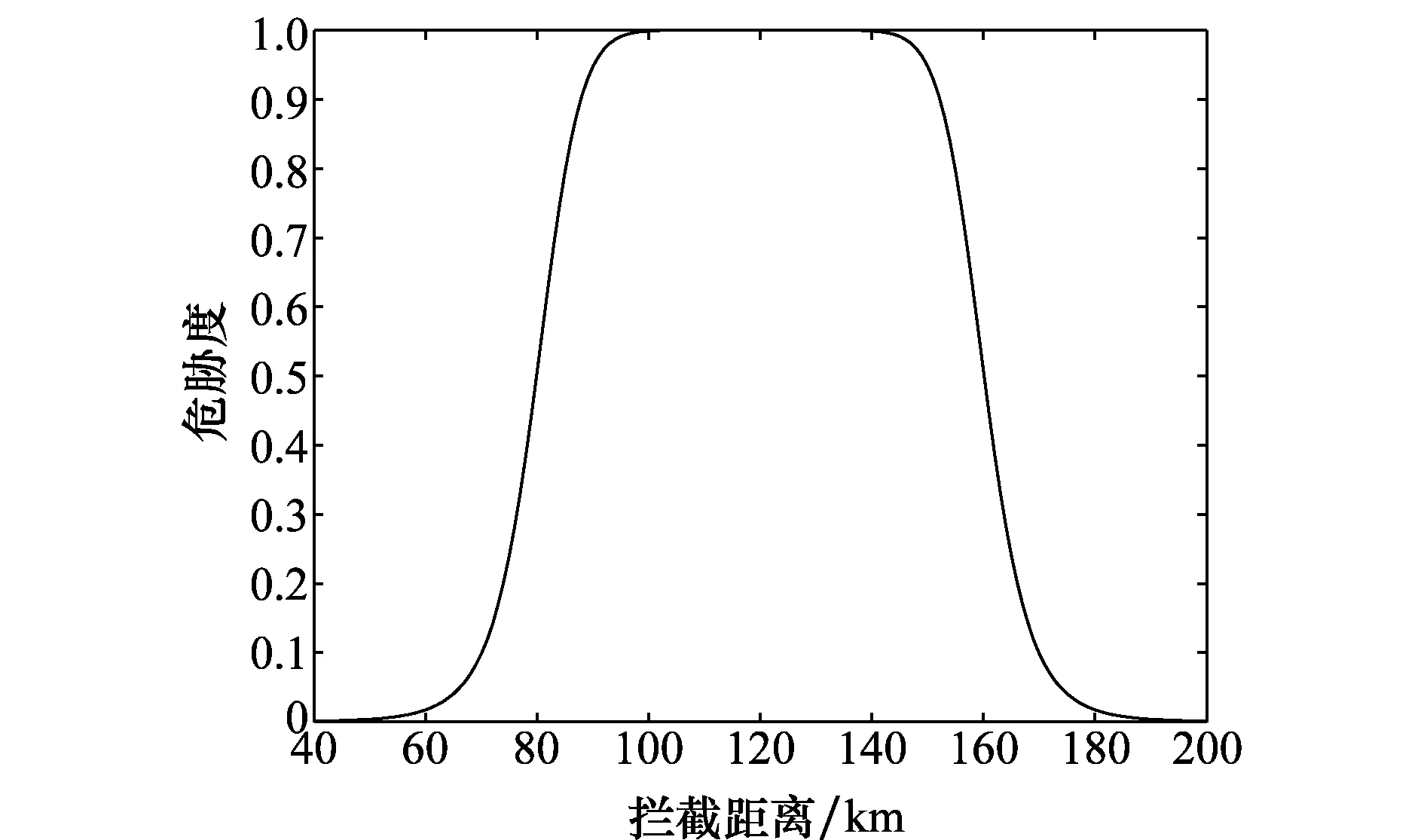
图3 威胁度随距离分布函数Fig.3 Threat distribution with range

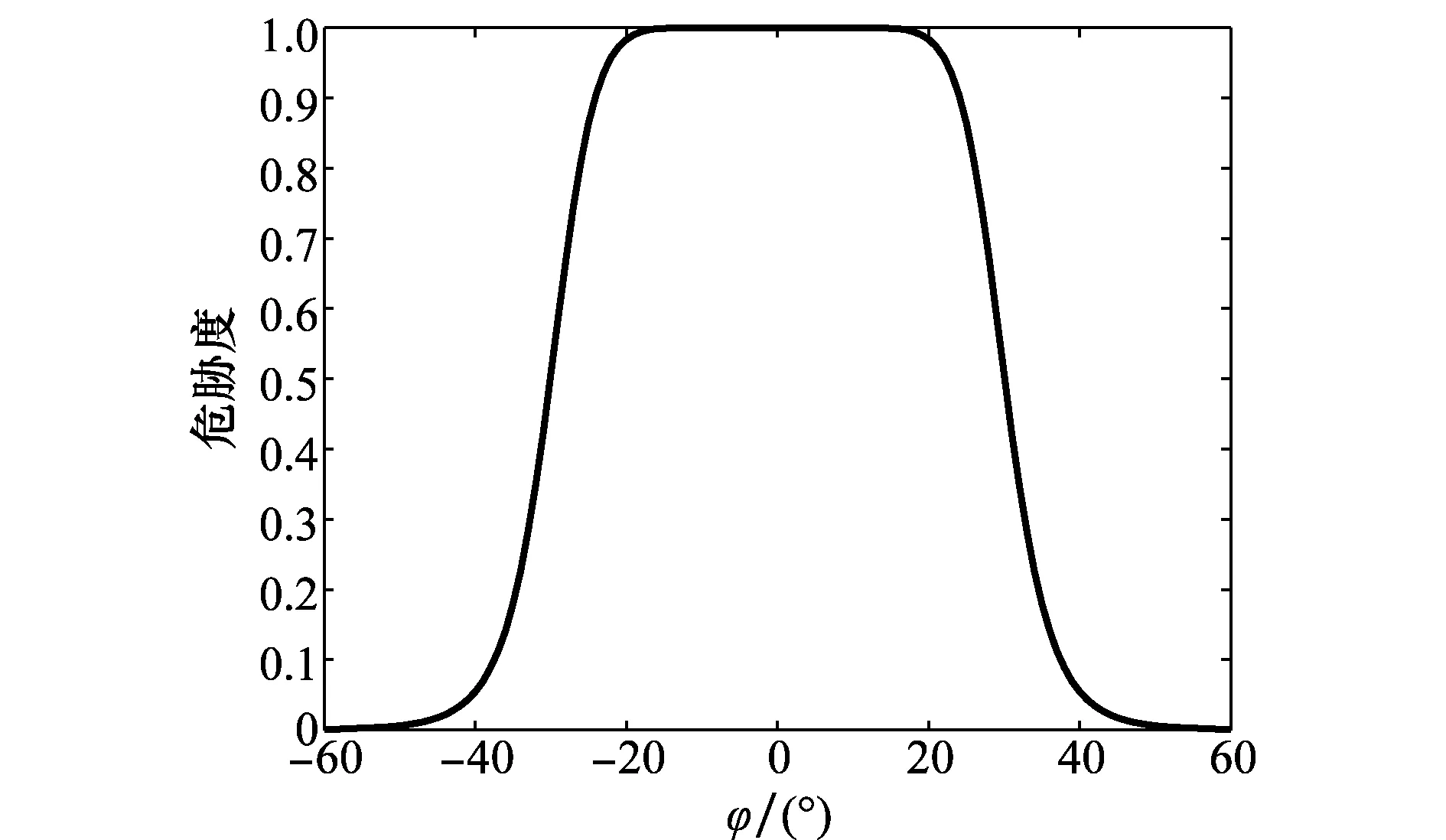
图4 威胁度随偏航角分布函数Fig.4 Threat distribution with yaw angle

(5)

式中,a1,b1,c1为钟形函数参数,a1,b1,c1共同决定了钟形函数的形状,a1表达式如式(6)所示,其中,n和b1决定钟形函数的宽度,c1为钟形函数中心轴的位置。

(6)

二维可拦截区的威胁度随拦截距离和发射偏航角分布,威胁度计算公式如下:

Ct=(y1·y2)1/3

(7)

对应图1中的掩护舰可拦截区而言,按照式(7)就算得到的威胁区分布图如图5所示,威胁最大为1,最小为0,威胁度为1表明该区域为不可逃逸区。

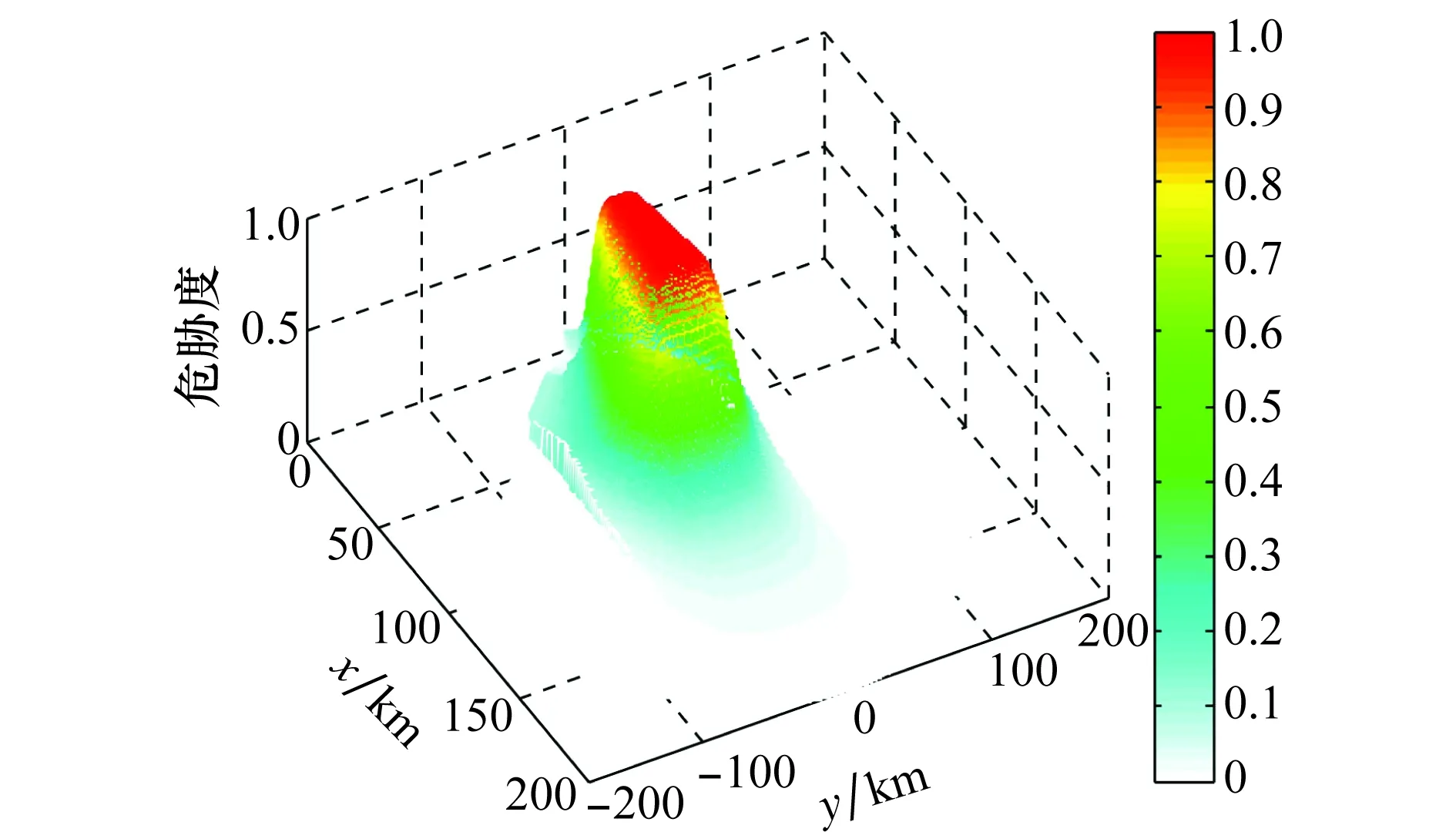
图5 掩护舰可拦截区威胁度分布图Fig.5 Threat distribution of warship intercept zone

综合以上3个影响因素,本文设计了掩护舰Cj对敌方导弹群体Ti的威胁度如下:

(8)

式中,Ct(l,φ)是掩护舰威胁度随l,φ计算的威胁度,l为导弹距离受保护目标的距离。

2 共生有机搜索算法

在通过以上的数学描述和分析,本文将海上多舰协同防空部署问题抽象成一个数学优化问题来求解。本文所采用SOS算法,其算法原理在于将原有的优化问题视为一个抽象的生态系统,系统中的每一个个体分别对应于原优化问题的一组解,每个个体的适应度值则对应于其解的性能指标函数,即本文中的式(1)。SOS算法通过不断模拟操作生态系统中常见的3种生态关系,即共生关系,共栖关系,及寄生关系产生新的个体,将适应度更好的新个体代替适应度较差的母体。SOS算法求解海上多舰协同防空部署优化问题的算法步骤如下。

步骤1生态系统初始化

在约束范围内随机生成种群规模为eco_size的初始种群,种群中每个个体由3个变量构成:Xi=[xi,yi,θi],x,y为第i个导弹点坐标,θi为掩护舰Ci的舷角。

步骤2适应度计算

根据式(1)计算每个个体的适应度,即该个体对应解的性能指标,对比所有个体,选出其中性能指标最优的个体,最优个体设为Xbest。

步骤3共生关系更新

SOS算法中共生关系,共生双方都可以从共生操作中收益,在当前种群中随机挑选两个个体Xi和Xj,共生操作后个体Xi和Xj均想向有益于自身的方向进化,其更新函数如式(9)所示。

(9)

式中,rand(0,1)表示向量模值在0到1之间的一个随机向量,向量维度与每个个体相同。Xbest为当前种群中的最优个体;VM为共生向量,其代表双方个体在解空间的中间点;BF是受益因子,进化过程中各个体的收益可能不相同,因此BF的取值随机为1或2。若Xi new的个体适应度小于Xi的个体适应度,则用Xi new取代Xi;若Xj new的个体适应度小于Xj的个体适应度,则用Xj new取代Xj。

步骤4共栖关系更新

SOS算法中共栖关系,仅有一个个体能够收益,而另一个个体将不会受到共栖关系的影响。对于种群中每个个体Xi,从种群其他个体中随机挑选一个个体Xj(Xj≠Xi),在共栖关系操作中不会改变,而Xi在共栖关系操作下更新如式(10)所示。

Xi new=Xi+rand(-1,1)·(Xbest-Xj)

(10)

式中,rand(-1,1) 表示向量模值在-1到1之间的一个随机向量,向量维度与每个个体相同。(Xbest-Xj)表示共栖关系中个体Xi栖身个体Xj所获得的进化方向矢量。若Xi new的个体适应度小于Xi的个体适应度,则用Xi new取代Xi。

步骤5寄生关系更新

SOS算法中寄生关系,对于寄生个体Xi,采用一个随机数代替其解向量上随机某个数值,从而生成了一个新的寄生向量VP,该寄生向量会从剩下的个体中随机挑选一个个体Xj作为其宿主,若宿主Xj的适应度函数小于寄生向量VP,则寄生成功,Xj被VP取代,否则,寄生失败,保留Xj。

步骤6判断当前是否满足算法的终止条件,如果满足,则输出Xbest防守最优部署策略;否则,则返回步骤3。

3 数值仿真分析

本节在想定的仿真条件下,通过SOS算法优化得到我方所有掩护舰的位置坐标和舰船舷角大小,使得式(1)中性能指标最小并满足所有约束。通过分析算法得到的最优解,判断该计算得到的最优防空部署是否能够应对当前来袭的导弹群体。

3.1 仿真算例1

共有5个来袭导弹群体,来袭导弹参数如表2所示,我方共有3艘掩护舰对受保护目标进行掩护,我方掩护舰参数如表3所示。我方掩护舰所携导弹类型对敌方来袭导弹的拦截概率如表4所示。我方保护舰需要在保护目标20 km范围内,并且任意两艘保护舰之间需要保持至少4 km的距离。

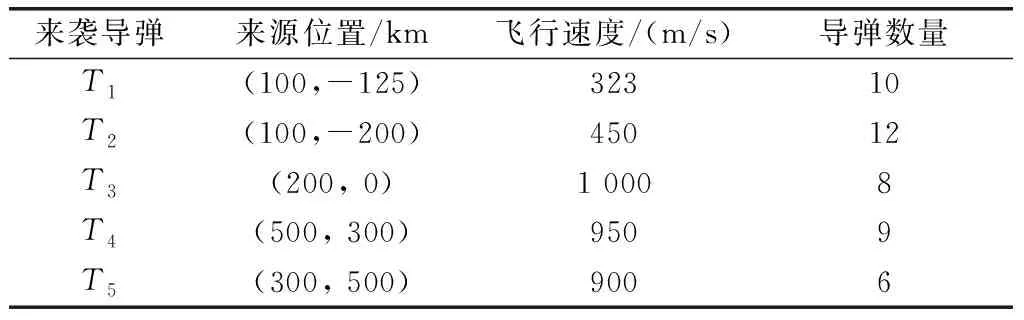
表2 敌方来袭导弹群体参数表(仿真1)

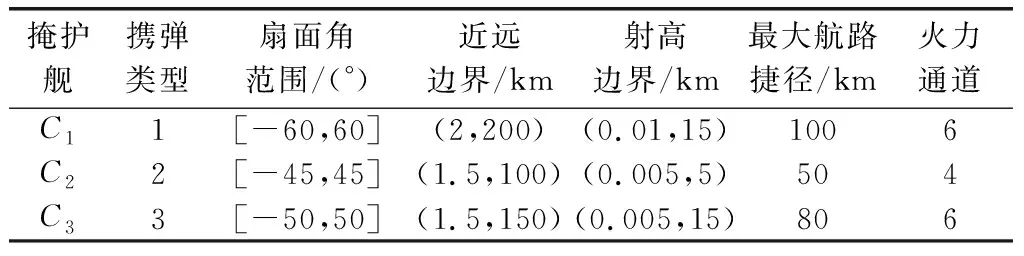
表3 我方掩护舰参数表(仿真1)

表4 拦截概率表(仿真1)

通过SOS算法得到的最优防空部署方案如表5所示。图6和图7为该部署方案下的威胁度分布图。图8为SOS优化算法与PSO算法在该仿真算例上的性能指标收敛图。

表5 我方掩护舰最优部署方案(仿真1)

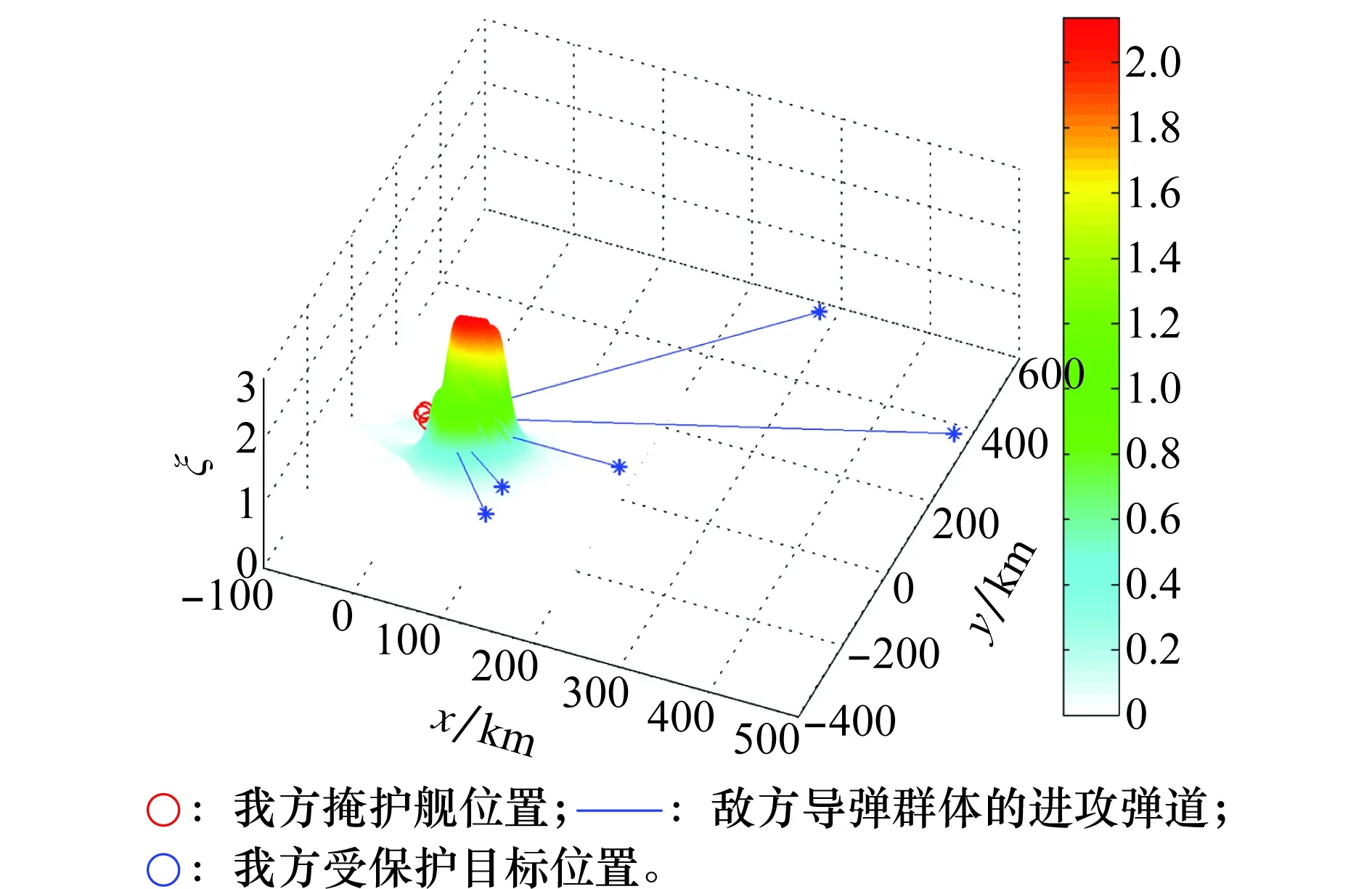
图6 掩护舰拦截威胁度三维分布图(仿真1)Fig.6 3-D threat distribution of warships (simulation 1)

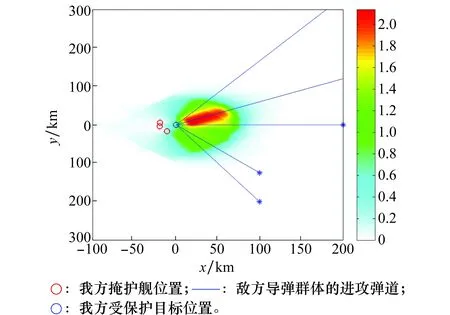
图7 掩护舰拦截威胁度平面分布图(仿真1)Fig.7 Threat distribution of warships in plane (simulation 1)

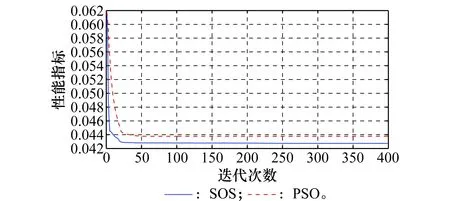
图8 SOS算法和PSO算法的性能指标迭代图(仿真1)Fig.8 Performance index iteration of SOS and PSO algorithm (simulation 1)

从掩护舰的防空部署方案以及该部署下的威胁度分布图来看,掩护舰的部署方案更倾向于正角度来袭的敌方导弹,特别是T4导弹群体,该群体导弹是高超声速高空巡航弹,且其群体数目高,对我方威胁度也最高,从掩护舰威胁度分布上看,该导弹弹道上将受到的拦截威胁也最高。对于同是超声速的T3和T5导弹去群体,该部署方案也能有效拦截。从图8可以看出SOS算法相较于PSO算法收敛速度更快,求得的性能指标更优,对于该问题获得了更优的解。

3.2 仿真算例2

共有7个来袭导弹群体,来袭导弹参数如表6所示,我方共有6艘掩护舰对受保护目标进行掩护,我方掩护舰参数如表7所示。我方掩护舰所携导弹类型对敌方来袭导弹的拦截概率如表8所示。我方保护舰需要在保护目标20 km范围内,并且任意两艘保护舰之间需要保持至少4 km的距离。

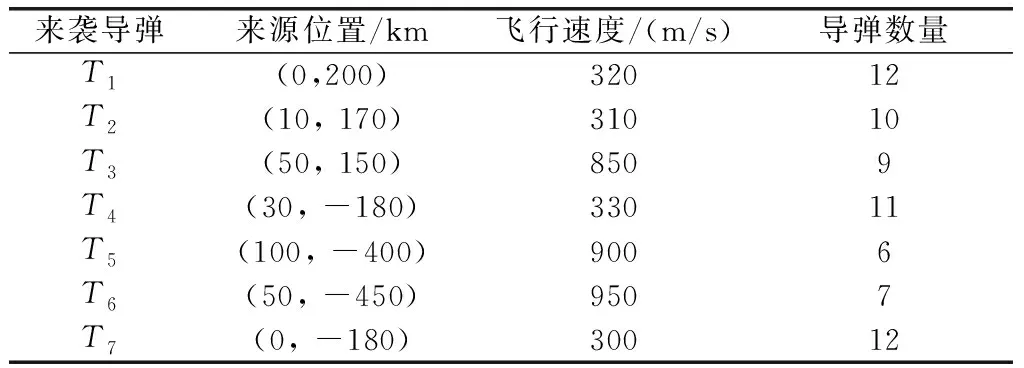
表6 敌方来袭导弹群体参数表(仿真2)

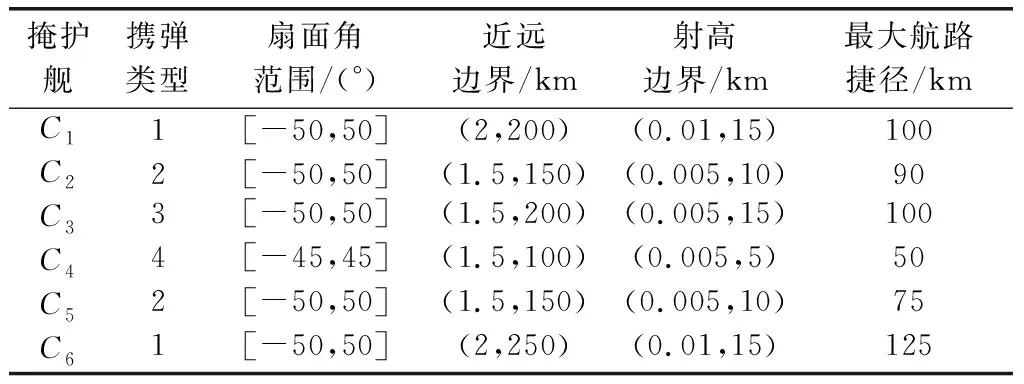
表7 我方掩护舰参数表(仿真2)

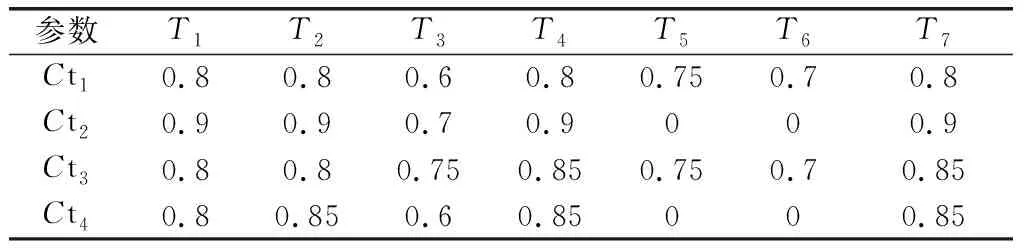
表8 拦截概率表(仿真2)

通过SOS算法得到的最优防空部署方案如表9所示。图9和图10为该部署方案下的威胁度分布图。图11为SOS优化算法与PSO算法在该仿真算例上的性能指标收敛图。

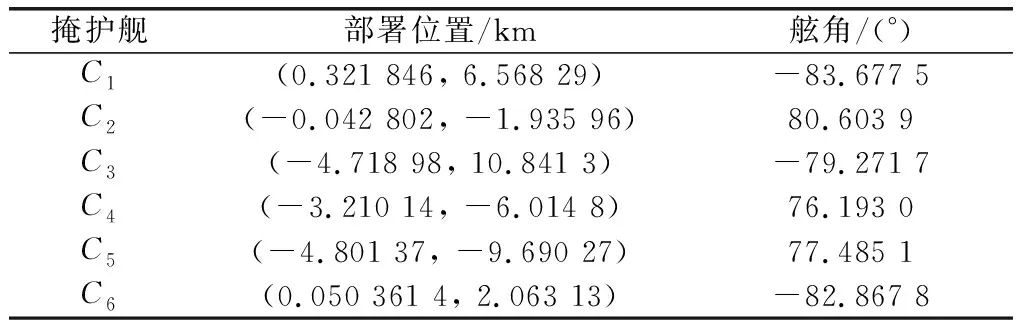
表9 我方掩护舰最优部署方案(仿真2)

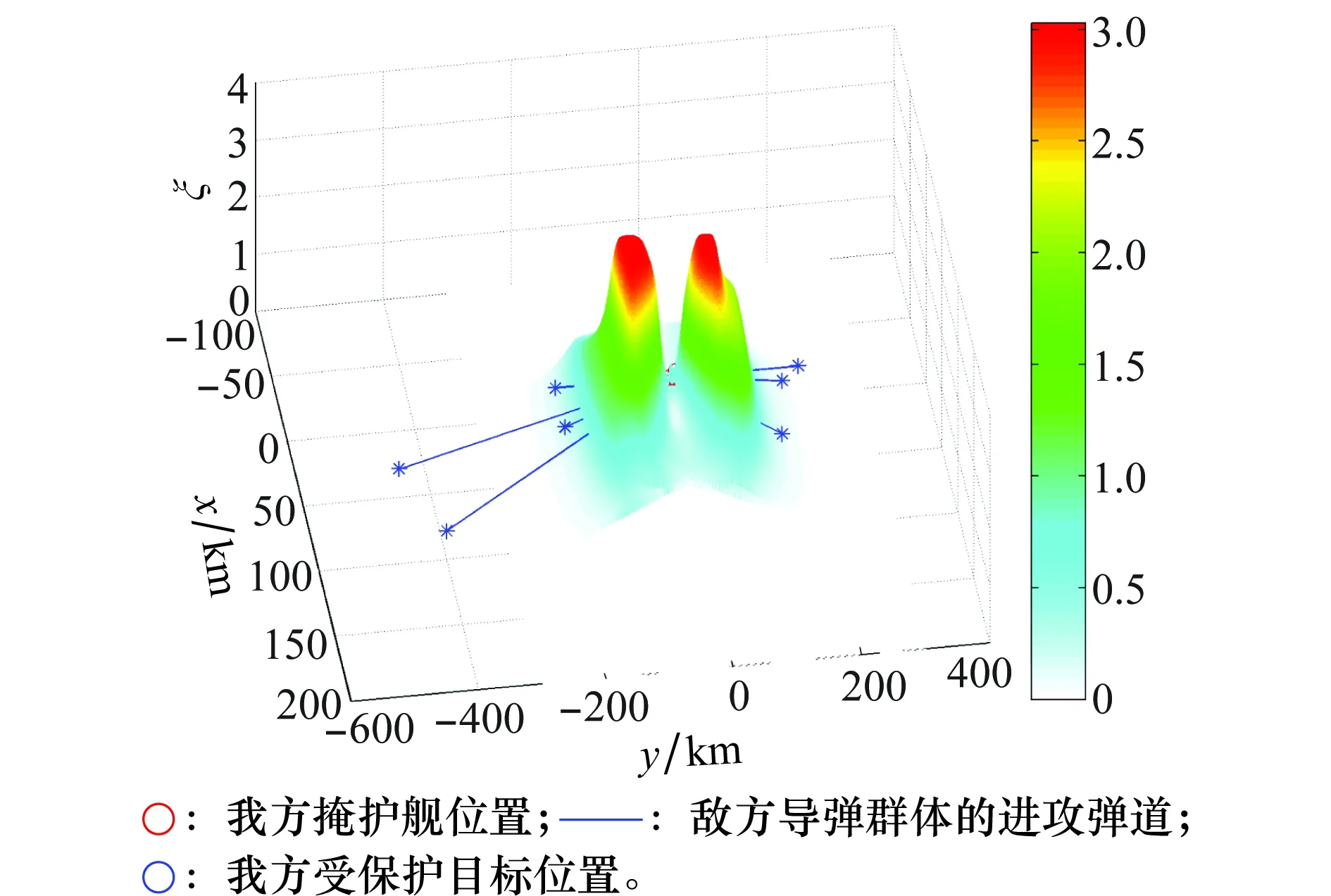
图9 掩护舰拦截威胁度三维分布图(仿真2)Fig.9 3-D threat distribution of warships (simulation 2)

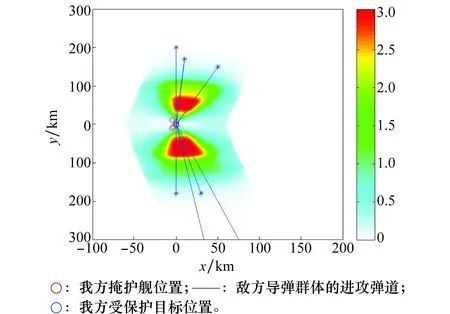
图10 掩护舰拦截威胁度平面分布图(仿真2)Fig.10 Threat distribution of warships in plane (simulation 2)

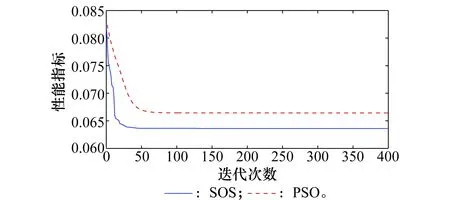
图11 SOS算法和PSO算法的性能指标迭代图(仿真2)Fig.11 Performance index iteration of SOS and PSO algorithm (simulation 2)

本算例中想定了一个较为极端的假设,即来袭导弹群体从2个相反的方向向受保护目标进攻,其中负方向的4个来袭导弹群体威胁度更高,相对而言正方向的3个来袭导弹群体威胁度相对较低。

从图7和图8中可以看出,优化得到的多舰协同防空部署方案分配了3搜掩护舰C1,C3,C6拦截负方向导弹群体,这些掩护舰的射高能够拦截高空巡航弹,可以拦截负方向来袭的导弹去群体。而C2,C4,C5掩护舰负责拦截正方向的低空反舰导弹。由此算例可看出,该算法能够有效解决各种可能的进攻态势下的多舰协同部署优化问题。图10中同样显示了SOS算法相较于PSO算法的优越性。

4 结 论

海上多舰协同防空部署是现代海上防空作战战术的重要问题之一,多舰协同防空部署可以根据当前侦测的敌方进攻态势、我方拥有的防御力量,对防区内有限的防御系统进行合理的部署优化,从而形成严密的防御体系,保护我方受保护目标的安全。

本文中对影响多舰协同防空效果的各因素进行了分析,得到了海上多舰协同防空部署优化的综合性能指标,提出了海上多舰协同防空部署优化问题的具体描述,并采用共生有机搜索算法对该问题进行了优化计算,最终得到最优海上多舰协同防空部署方案。在最后的数值仿真结果中可以看出,SOS算法相比传统的智能算法能够快速有效地求解不同进攻态势下的掩护舰协同防空部署方案使得综合性能指标最小并满足所有约束条件。