海杂波环境下改进的中值矩阵检测方法
2018-10-15赵文静金明录刘文龙
赵文静, 金明录, 刘文龙
(大连理工大学信息与通信工程学院, 大连 辽宁 116024)
0 引 言
海杂波背景下的目标检测问题在军事和民用上都占有重要的地位。因此,很多学者致力于研究海杂波环境下的目标检测机制[1-2]。在均匀背景下,基于多普勒功率谱估计的单元平均恒虚警率检测方法(cell averaging constant false rate, CA-CFAR)取得较好的检测性能[3]。然而,在短脉冲序列的脉冲多普勒雷达系统下,由于杂波谱展宽、多普勒滤波器组的能量泄露及较低的多普勒分辨率等原因使得CA-CFAR方法的检测性能严重下降。
文献[4]从几何角度考虑了雷达目标检测问题,并设计了基于协方差矩阵的几何检测方法,其检测机制如图1所示。由所有正定矩阵构成的空间称为矩阵流形,相应的检测方法称为矩阵CFAR 方法。此外,文献[5-11]将基于黎曼度量的矩阵CFAR方法应用于其他雷达目标检测场景中,并取得较好的检测性能。矩阵CFAR方法与经典的CA-CFAR方法的主要区别是,在每个距离单元内,由接收数据的协方差矩阵代替了经过滤波处理的采样数据。由于矩阵CFAR方法不需要进行FFT变换,从而克服了CA-CFAR方法的缺点。矩阵CFAR方法的另一个特点是利用矩阵流形的几何结构求解参考单元的均值协方差矩阵。最后,利用两个协方差矩阵之间的距离衡量信号存在与不存在时的差异性。理论分析和仿真实验表明,基于信息几何的检测方法的检测性能优于传统的CA-CFAR方法[12]。基于以上工作,为了消除参考单元的协方差矩阵中异常点的影响,文献[13]提出了中值矩阵检测方法。此外,利用矩阵流形上不同的几何测度,文献[14]提出了几种不同的检测方法并取得了较好的检测性能。但是这类方法取得较好的检测性能是以较高的计算复杂度为代价的,这一原因也限制了其实际应用。
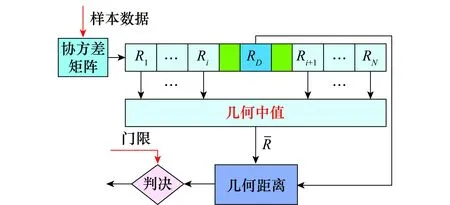
图1 基于信息几何的中值矩阵检测方法程序框图Fig.1 Block diagram of median matrix CFAR detector based on information geometry
本文的主要目的是寻找一种新的统计量代替几何距离,从而减少算法的计算复杂度。海杂波数据存在相关性,如何利用海杂波的相关性是提高检测性能的一种新的思路。文献[15-18]将基于特征值的检测方法及其修正方法应用于认知无线电网络中的频谱感知问题。由于这类方法利用特征值捕捉了信号间的相关性,从而取得了较高的检测性能。另一方面,主特征值可以提取数据的主要信息[19]。特别是秩1矩阵,最大特征值具有重要作用。因此,本文针对秩1信号提出了基于最大特征值的检测方法,主要创新点如下:在具有相关性的海杂波环境下,利用矩阵CFAR方法的检测机制,我们设计了一类基于最大特征值的全盲检测方法。由于所提方法只利用最大特征值进行检测,与现有的几何方法相比,所提方法具有较小的计算复杂度。同时,由于特征值可以捕捉数据间的相关性,因此所提方法进一步提高了检测性能。
1 系统模型
假设在一个相干处理间隔(coherent processing interval, CPI)内雷达发送M个脉冲。接收数据经过采样等处理后形成M维矢量y,存储在由参考单元,检测单元,保护单元构成的滑动窗内。存储在检测单元(cell under test, CUT)内的数据称为主要数据,存储在参考单元内的数据称为辅助数据cl,假设参考单元的个数为N。不失一般性,海杂波背景下的检测问题可以表示为如下的二元假设检验模型:
(1)
在零假设H0下,假设接收数据中只含有杂波c。在另一假设H1下,接收数据由杂波c及回波信号s构成。不失一般性,在均匀环境下,假设主要数据和辅助数据是独立同分布的。因此,可以利用参考单元内的辅助数据获取检测单元内的杂波信息。
回波信号可以表示为s=ap,其中a=Aexp(jθ)表示目标信号的复幅度。在实际中,a为复常数或未知的随机变量,用于表示目标的横截面积以及信道传播衰减系数。p是多普勒导向矢量,表示为
(2)
式中,fd表示目标信号的多普勒频率;fr为脉冲重复频率。
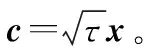
(3)
其中,γ,ν分别为尺度参数、形状参数;Γ(·)是伽玛函数;Kv-1(·)表示v-1阶第二类修正贝塞尔函数。一般,形状参数ν的取值范围是(0,∞),ν的取值越小表示杂波的海尖峰越明显。
2 基于最大特征值的中值矩阵检测方法
考虑到海杂波的相关性,本文采用特征值提取数据间的相关性。进一步,利用最大特征值作为检测统计量,代替现有几何方法中的中值矩阵和检测单元内的协方差矩阵之间的距离。由于矩阵流形上不同的几何测度,对应不同的检测性能。该节首先回顾了利用不同几何测度估计中值矩阵的方法。基于此,提出基于最大特征值的检测方法。
2.1 几种中值矩阵
所有的Hermitian正定协方差(Hermitian positive definite, HPD)矩阵构成的几何空间,称为矩阵流形。与欧氏空间不同,在矩阵流形上存在多种几何测度。首先,介绍Hellinger测度及对应的Hellinger中值矩阵[20]。
设A,B为两个HPD矩阵,它们之间的Hellinger距离可以表示为
(3)
假设R1,R2,…,RN是参考单元内的协方差矩阵,R是检测单元内的协方差矩阵,令
(4)
参考单元的中值矩阵可以通过求解下列优化问题获得
(5)
在本文中,采用梯度下降法估计中值矩阵。式(4)的梯度向量表示为
(6)
梯度向量的范数表示为
(7)
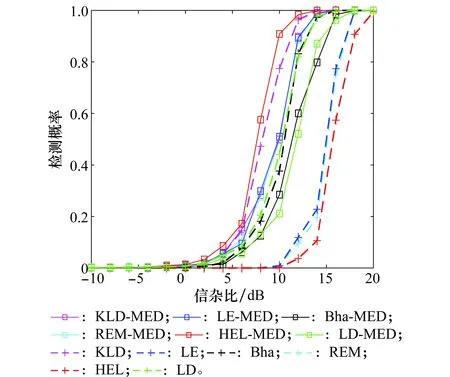
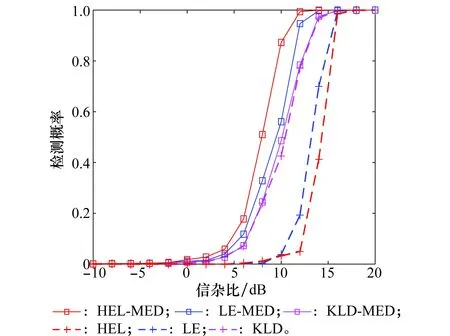
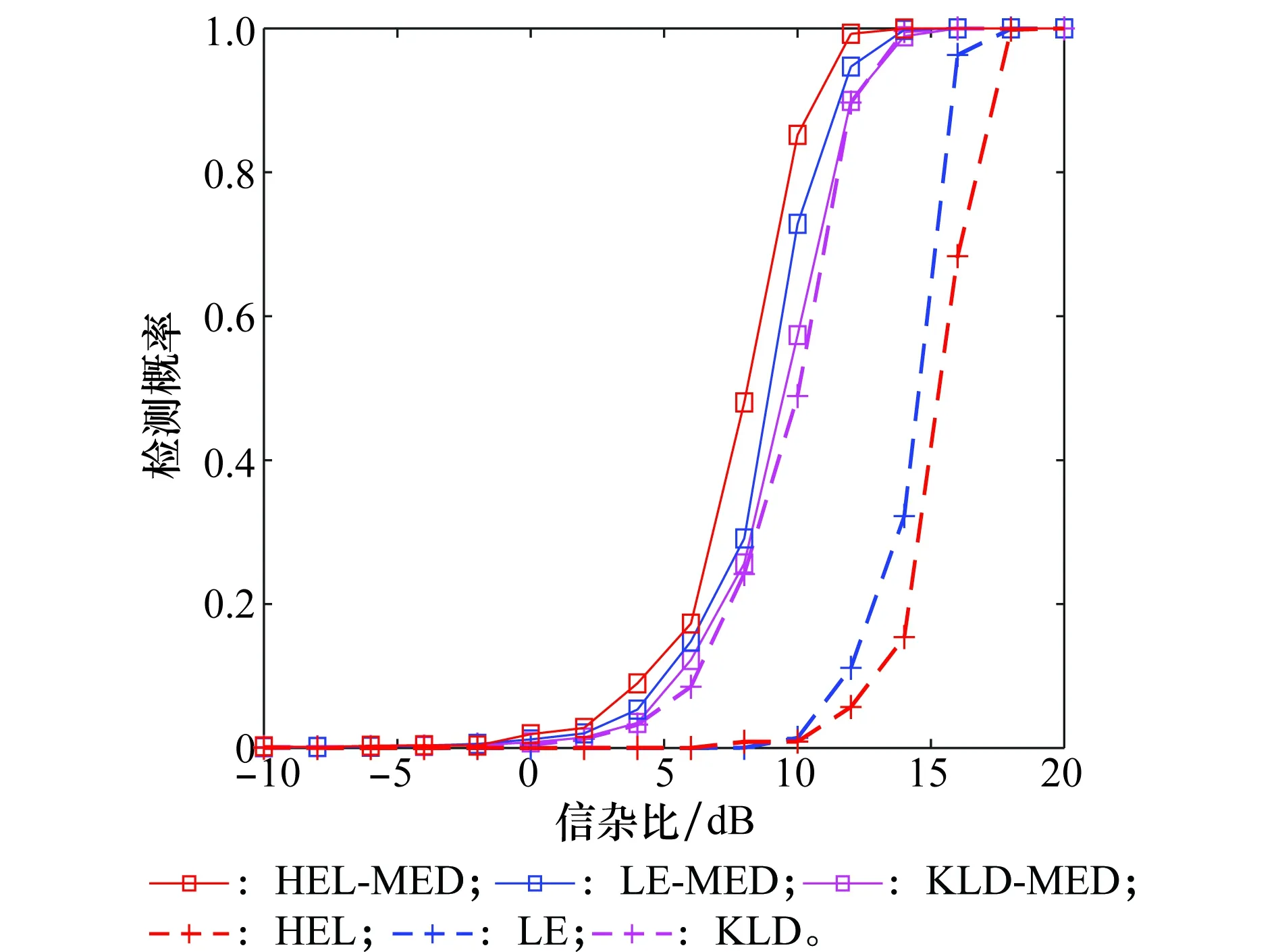
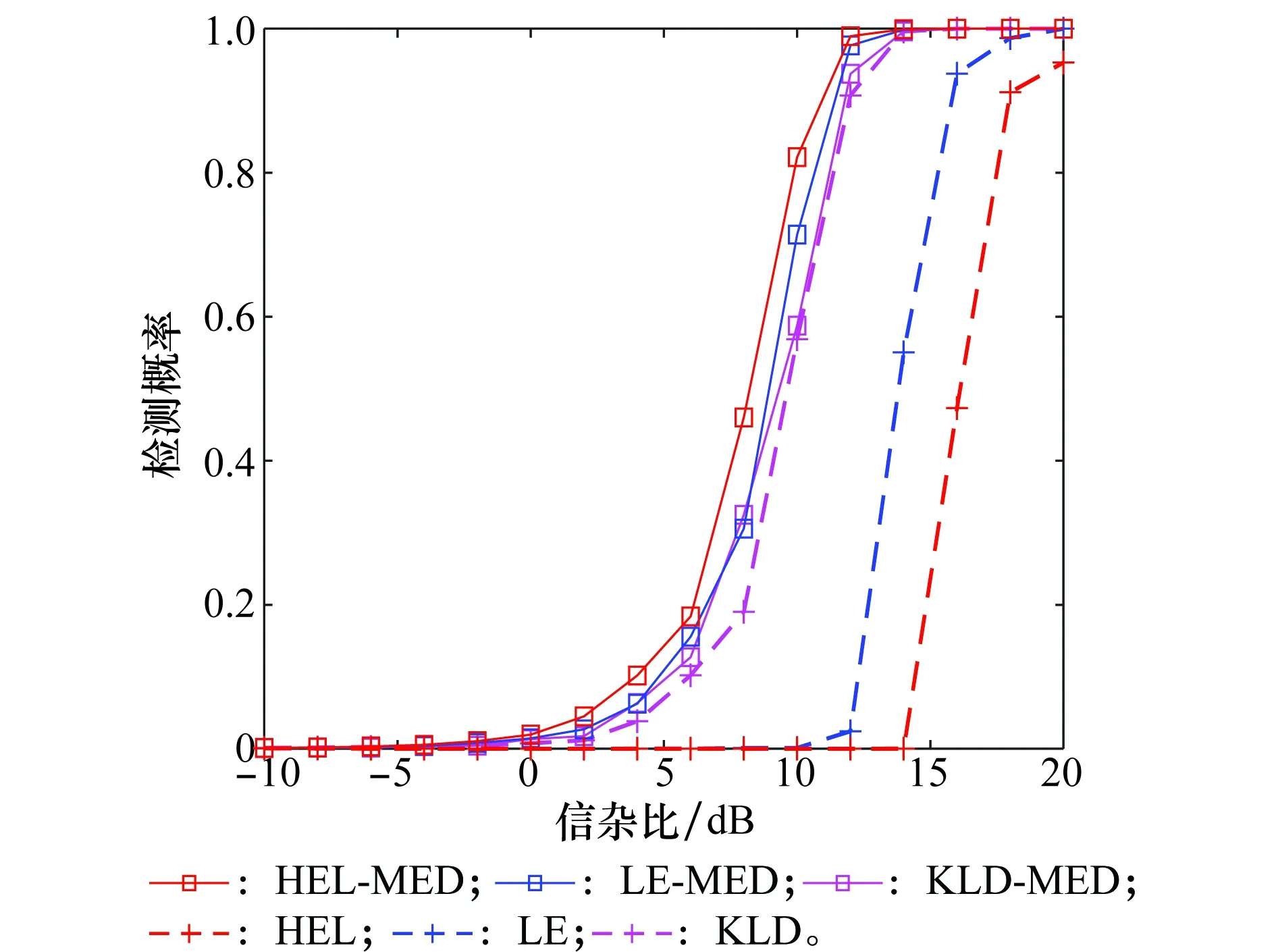
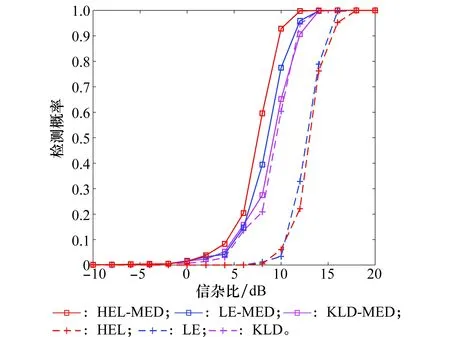
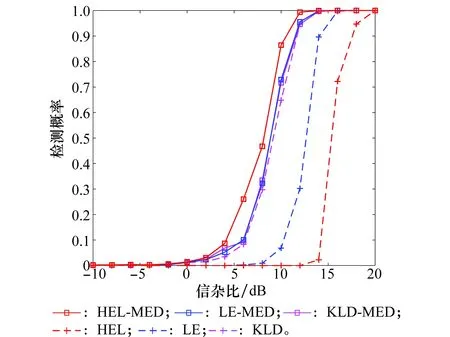
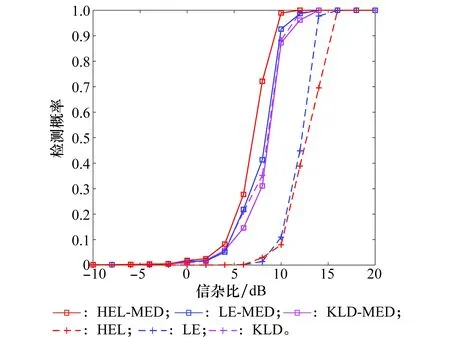
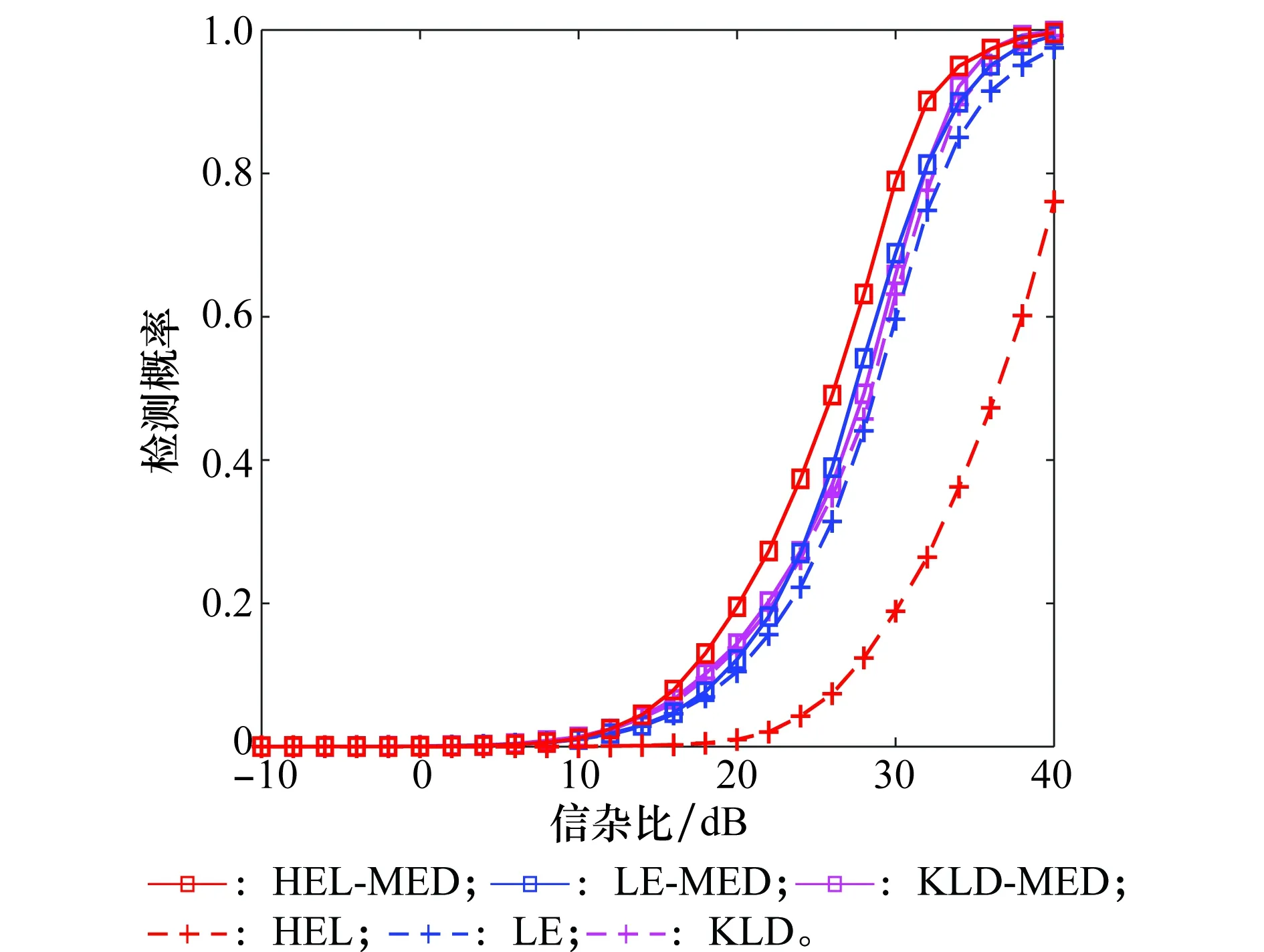
令ε为精度值,Nit为最大迭代次数。当NR<ε时,或者迭代次数满足t (8) 在矩阵流形上,除了Hellinger散度之外,还有其他的散度定义,如Kullback-Leibler散度、Log-Determinant散度、Log-Euclidean散度、Bhattacharyya散度和Riemannian散度。采用与求解Hellinger中值矩阵类似的方法,可以得到相应的中值矩阵。具体的散度定义以及相应的中值矩阵估计值如表1所示。 表1 基于不同几何测度的中值矩阵估计值 在短脉冲序列下的脉冲多普勒雷达系统中,与基于多普勒功率谱估计的CA-CFAR方法相比,基于信息几何的矩阵CFAR方法的检测性能有所提高。其主要原因是矩阵CFAR方法很好地利用了矩阵流形内在的几何结构,“准确”求解了中值矩阵。尽管如此,有的矩阵CFAR检测算法的检测性能却不够理想。例如,基于Hellinger散度的中值矩阵检测器是从几何角度出发,提出的一种新的检测方法,但是它的检测性能较差[14]。造成其性能较差的主要原因是检测统计量很大程度上依赖于矩阵的行列式,而对于信号存在与不存在两种情况下的行列式变化并不大,不能很好地衡量他们之间的差别。 为此,我们修正了基于Hellinger散度的矩阵检测方法,保留原算法中的中值矩阵的计算方法,但采用最大特征值作为判决统计量,其检测机制如图2所示。 图2 基于最大特征值的中值矩阵检测方法的检测机制Fig.2 Detection scheme of median matrix detection methodbased on the maximum eigenvalue (8) 类似的,将最大特征值与其他几种散度相结合,可以得到6种新的检测方法,表2给出了原矩阵CFAR算法和修正算法的符号表示。 表2 现有矩阵CFAR算法和修正算法的符号表示 在以下的仿真实验中,为了与现有矩阵CFAR检测方法进行比较,参数设置与参考文献[14]保持一致。假设慢速运动目标的多普勒频移为3.83 Hz,脉冲重复频率为1 000 Hz。在一个CPI内,假设雷达发送8个脉冲,参考单元的个数为16个,虚警概率为pfa=10-3,信杂比(signal-clutter ratio,SCR) 在-10~20 dB范围内。假设海杂波服从K分布,由球不变随机过程产生。在实际环境中,海面雷达散射回波的多普勒谱反映了海面自身的动态调整特性,强烈影响着海面目标探测的性能。海杂波的多普勒频移和展宽是体现海杂波谱的重要因素[21]。为此,本文主要考虑以下几种场景:①海杂波多普勒频移fdc=0 Hz时,海杂波频谱3 dB带宽分别为40 Hz和80 Hz的场景;②海杂波多普勒频移fdc=3 Hz和展宽80 Hz的场景;③海杂波多普勒频移fdc=3 Hz,展宽80 Hz,杂波噪声比CNR=0 dB的场景;④海杂波多普勒频移fdc=65 Hz,展宽80 Hz,目标多普勒频移为80 Hz。 首先,针对无杂波多普勒频移和无杂波谱展宽情景,对所提方法与现有的矩阵CFAR方法进行比较,如图3所示。从仿真结果来看,原有算法和修正算法性能表现不一,有的修正算法优于原算法,但有不如原算法。KLD算法是现有的矩阵CFAR方法中最优的,但是所提的HEL-MED方法明显优于KLD方法。 图3 无杂波谱展宽时,基于最大特征值与基于几何距离的矩阵CFAR方法检测性能比较 Fig.3 Detection performance comparison of M-CFAR based on the maximum eigenvalue and the existing M-CFAR detectors in the environment without clutter spectrum broadening 图4 存在杂波谱展宽时,基于最大特征值与基于几何距离的矩阵CFAR方法检测性能比较 Fig.4 Detection performance comparison of M-CFAR based on the maximum eigenvalue and the existing M-CFAR detectors in the environment with clutter spectrum broadening 其次,针对无杂波多普勒频移和有杂波谱展宽的情景,将所提方法与现有的矩阵CFAR方法的检测性能进行比较。为了方便,图4只显示了所提方法中较好的3种方法:HEL-MED,LE-MED及KLD-MED与原有方法HEL,LE及KLD三种方法的检测性能曲线。与无杂波谱展宽情况相比,所有方法的检测性能均有下降,但是所有修正算法都优于原算法。特别的,HEL-MED方法仍然是最优的,且LE-MED,KLD-MED方法也优于KLD方法。 除此之外,我们考虑了在杂波谱展宽的条件下,存在干扰目标的非均匀检测环境。图5描述的只有一个干扰目标,干扰杂波比(ICR)为2 dB的场景;图6描述的是存在2个干扰目标, 且ICR与SCR相同的场景。 图5 存在杂波谱展宽及1个干扰目标时,基于最大特征值与基于几何距离的矩阵CFAR方法检测性能比较 Fig.5 Detection performance comparison of M-CFAR based on the maximum eigenvalue and the existing M-CFAR detectors in the environment with one interfering target 图6 存在杂波谱展宽及2个干扰目标时,基于最大特征值与基于几何距离的矩阵CFAR方法检测性能比较 Fig.6 Detection performance comparison of M-CFAR based on the maximum eigenvalue and the existing M-CFAR detectors in the environment with two interfering targets 从图5和图6可知,当存在干扰目标时,所有方法的性能均下降,但是基于最大特征值的检测方法仍优于现有矩阵CFAR方法。且从图6可以看到,随着干扰的增强,所有方法的检测性能下降较少,主要原因是中值矩阵较好地克服了参考单元协方差矩阵中异常点的影响。 以上的仿真环境中假设杂波的多普勒频移为0,然而,由于风等其他因素的影响使得杂波的多普勒频移可能不为0。首先考虑了杂波多普勒频移较小的场景,设杂波的多普勒频移为fdc=3 Hz。对所提方法与现有的矩阵CFAR方法的性能进行比较,实验结果如图7所示。根据图7中的检测性能曲线可知,在考虑海杂波多普勒特性的检测背景下,所提方法仍优于现有的矩阵CFAR方法。 图7 海杂波谱展宽80 Hz及平均多普特频移为3 Hz条件下,基于 最大特征值与基于几何距离的矩阵CFAR方法检测性能比较Fig.7 Detection performance comparison of M-CFAR based on the maximum eigenvalue and the existing M-CFAR detectors under the condition that bandwidth and mean Doppler shift of sea clutter are 80 Hz and 3 Hz 图8描述的是在杂波与噪声混合的复杂背景,所提方法与其他矩阵CFAR方法的检测性能曲线。假设杂波的多普勒频移为3Hz,杂波谱展宽为 80Hz,杂波与噪声比为0 dB。从图8可知,在杂波与噪声混合的检测背景下,本文方法的性能仍优于现有矩阵CFAR方法。但与图7相比,由于白噪声的影响,所有方法的性能均下降。 图8 海杂波与噪声混合背景下,基于最大特征值与基于几何距离的矩阵CFAR方法检测性能比较 Fig.8 Detection performance comparison of M-CFAR based on the maximum eigenvalue and the existing M-CFAR detectors under the mixture of clutter and noise 除此之外,本文还考虑了海杂波平均多普特频移为65 Hz,目标多普勒频移为80 Hz的检测场景,结果如图9所示。在目标多普勒频移较大的场景,所提方法的性能仍由于现有的矩阵CFAR检测方法。 图9 海杂波平均多普特频移为65 Hz,目标多普勒频移为80 Hz 条件下,基于最大特征值与基于几何距离的矩阵CFAR方法检测性能比较 Fig.9 Detection performance comparison of M-CFAR based on the maximum eigenvalue and the existing M-CFAR detectors under the condition that mean Doppler shift of sea clutter is 65 Hz and target Doppler shift is 80 Hz 为了进一步验证所提方法的鲁棒性,本文利用实测海杂波数据进行了算法性能的对比实验。本文采用的实测数据是由加拿大McMaster 大学提供的1993年IPIX雷达数据的第17号文件,检测性能如图10所示。根据实验结果可知,改进的矩阵CFAR检测方法的性能优于原有的矩阵CFAR方法。 图10 基于最大特征值与基于几何距离的矩阵CFAR方法在实测海杂波环境下的检测性能比较 Fig.10 Detection performance comparison of M-CFAR based on the maximum eigenvalue and the existing M-CFAR detectors by the real sea clutter data 综合以上的仿真结果来看,与原有基于几何距离的方法相比,基于最大特征值的改进中值矩阵CFAR检测算法具有明显的性能优势和性能鲁棒性。值得关注的是基于Hellinger距离的原算法在以上所有场景中检测性能最差,但是基于最大特征值的改进HEL算法(HEL-MED)却表现出最好的性能。这说明HEL原算法中的中值矩阵计算比其他算法受杂波环境影响更小,基于最大特征值的信息积累性能更好,这有待于进一步深入研究。 最后,我们比较并分析了所提算法与现有矩阵CFAR方法的计算复杂度。令一次加法或者一次乘法作为一次基本运算量,将算法中所有基本运算量的总次数作为算法的计算复杂度[22]。由于所提方法与原方法采用相同的方法求解中值矩阵,因此,只考虑算法中不同部分的计算复杂度的差异。如表3所示,基于Kullback-Leibler散度、Log-Determinant散度、 Log-Euclidean散度、 Bhattacharyya散度、Riemannian散度和Hellinger散度的矩阵检测方法的计算复杂度较高,其中,M表示脉冲序列的长度,N为参考单元的个数。通过比较分析得出,所提算法的计算复杂度较低,使得在实际检测环境中易于实现。 表3 算法复杂度分析 本文主要研究了海杂波背景下的短脉冲多普勒雷达的目标检测问题。采用现有矩阵CFAR方法的检测结构,保留了原算法中的中值矩阵的求解方法,以保持原算法的优势,但是采用最大特征值作为检测统计量,给出了新的全盲检测策略。根据矩阵流形上不同的几何测度,设计了6种不同的中值矩阵检测方法。此外,复杂度分析表明所提算法比现有几何方法具有更低的计算复杂度。最后,通过实测数据和对是否存在杂波谱展宽、杂波多普勒频移和白噪声,以及多个目标干扰的检测环境进行了仿真实验分析,结果表明所提算法具有较优的检测性能和鲁棒性,特别是最大特征值与Hellinger散度中值矩阵相结合的新算法(HEL-MED)表现出最优的性能。
2.2 基于最大特征值的中值矩阵检测方法
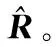

3 仿真实验

4 结 论
