基于认知的抗折叠扩展杂波波形设计方法

张 洋, 位寅生

(哈尔滨工业大学电子与信息工程学院, 黑龙江 哈尔滨 150001)

0 引 言

高频天波雷达[1]通过电离层反射来探测目标,而雷达作用距离超过信号形式决定的最大无模糊测距范围,远距离杂波会经距离折叠进入雷达接收机。电离层非平稳性将破坏回波相位相干性,远距离折叠杂波因多次经过电离层反射,导致其在频谱上展宽现象严重,这种折叠扩展杂波将淹没低速弱目标,严重影响目标检测性能。

一部分学者从信号处理角度来实现这种扩展杂波的抑制。文献[2]利用Wigner-Ville分布来补偿电离层相位扰动。文献[3]介绍了相位梯度法与最小熵谱法实现电离层相位补偿。文献[4-5]介绍了一种基于多项式相位建模的方法来抑制电离层杂波。这些方法可总结为对电离层相位污染函数进行估计,进而通过提取的相位污染函数对扩展杂波相位进行补偿,使扩展杂波压窄,将压窄的杂波抑制,再通过提取出的相位污染函数恢复目标信号。

此外,波形设计一直是缓解距离折叠扩展杂波影响的有效手段。文献[6]采用一种高重频步进信号,利用其波形特性及高分辨处理来实现折叠杂波抑制,但这种方法在高频雷达中并不适用。文献[7]采用3组重频信号,对距离折叠杂波进行抑制。文献[8]通过发射二重频频率信号,进而通过逻辑映射处理实现距离折叠杂波的抑制,但这种方法降低了多普勒分辨能力。文献[9-11]采用一种非并发波形(non-recurrent waveform,NRWF)来抑制距离折叠杂波,这种波形能将折叠杂波从低多普勒区域搬移到高多普勒区域,从而改善低速目标的检测性能,但这种方法牺牲了部分高多普勒检测区域,不利于对高速目标进行检测。文献[12]将非并发波形与空时自适应处理结合来抑制折叠扩展杂波。

从文献[2-5]信号处理方法与文献[9-11]提出的NRWF得到启发,本文在NRWF的基础上提出一种脉间相位编码信号来抑制折叠扩展杂波。这种波形的设计首先要通过回波信号提取电离层相位污染函数,即慢相径调制函数[13],进而将提取的污染函数用于信号脉间相位码的设计。设计好的脉间相位编码信号可实现折叠扩展杂波在多普勒谱上压窄并且搬移到指定区域,由于扩展杂波已被压窄,在多普勒谱上很容易找到一小块无目标区域来“安置”压窄的杂波,实现杂波与目标的分离。

由于电离层的时变特性,这种波形只能在某一段时间内工作,当电离层相位污染函数随时间逐渐改变时,波形使杂波压缩与搬移的能力将逐渐失效,因此引入认知的思想。认知雷达[14-16]通过回波中包含的环境信息,可以自适应的设计发射波形来适应非平稳的环境。在一段时间内,慢相径调制函数是准周期的,因此可以预测出下一段时间内电离层慢相径调制函数,可将预测的慢相径调制函数作为先验信息设计波形参数。由于电离层具有非平稳性,可以实时地对相位污染函数进行预测,实现波形脉间相位码的实时更新,进而适应时变的电离层。这种方法可以有效抑制经电离层非线性相位调制的距离折叠扩展杂波,极大改善雷达的检测能力。

1 问题描述与杂波模型

天波雷达在实现超视距探测的同时,远距离折叠杂波以电离层作为传输媒介与目标信号一同进入雷达接收机,同时由于电离层非平稳性,折叠杂波在频谱上展宽严重,不利于目标检测。

本节通过线性调频连续波信号来分析杂波距离折叠与展宽原因。为表示方便,本文采用复数形式表示雷达发射与接收信号,线性调频连续波信号如下所示:

(1)

(2)

式中,T为信号重复周期;N为相干积累时间内波形重复周期数;k为调频斜率;f0为载频。

经过m次距离折叠,杂波回波如下所示:

uR(t)=

(3)

式中,τ=mT+τ0为回波信号时间延迟;m为杂波折叠次数;M(t)为电离层慢相径调制函数。

杂波进入接收机经过混频解调处理,输出的第n个脉冲相位如下所示:

(4)

通过式(4)可见,M(t)为电离层慢相径调制函数,造成回波信号相位非线性调制,而-2πkτ0mT为一常数,可忽略,即当m不为0时,无法分辨,产生距离模糊。

本节采用正弦模型[2,5]作为电离层慢相径调制函数M(t)。

M(t)=asin(w0t+θ),t=0,T, …, (N-1)T

(5)

电离层慢相径调制函数可经过泰勒公式展开成多项式和的形式:

(6)

式中,di为多项式中第i项系数。

在式(6)中,展开多项式中常数项可忽略,一次项为线性项,会造成杂波在频谱上搬移,其他非线性项会造成杂波在频谱上展宽。

电离层慢相径调制函数可以看作准周期的,所以通过认知雷达获得的一段时间内电离层杂波相位污染函数可以预测未来一段时间内电离层杂波相位污染函数。在一定误差范围内,一段有限时间内的电离层杂波相位污染函数可以展开为有限阶多项式的和,则预测的污染函数Mpre(t)为

(7)

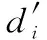
针对上文介绍杂波特性,希望利用杂波信息设计一种波形能使扩展折叠杂波在回波距离多普勒处理后已压缩成一较窄杂波,并搬移到频谱上指定位置,实现折叠扩展杂波的抑制。

2 抗折叠扩展杂波波形设计

2.1 基于电离层扰动认知的脉间相位编码信号

由于电离层的时变特性,在此引入认知的思想。认知雷达通过回波中环境与目标信息,可以自适应的设计发射波形来适应非平稳的环境。

本文引入认知的思想,通过雷达处理机对接收到的回波信号进行处理,从扩展杂波中提取杂波信息作为下一次发射的先验信息,用于更新下一次发射波形的波形参数,形成一个闭环反馈系统。认知雷达框图如图1所示。

基于认知的脉间相位码信号设计步骤如下:

步骤1处理接收到的回波,检测目标并提取杂波信息;

步骤2将步骤1获得的先验信息用于预测电离层相位污染函数;

步骤3更新波形脉间相位码;

步骤4发射更新后的波形;

步骤5对回波处理,杂波若压缩,转到步骤4,若杂波未压缩,转到步骤1。

图2为本文介绍的基于认知的脉间相位编码信号设计流程整体设计过程。

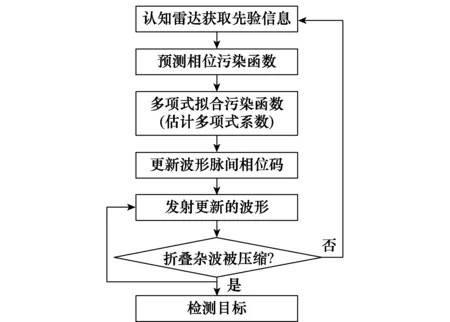
图2 基于认知的脉间相位编码信号设计流程Fig.2 Design process of the inter-pulse phase coded waveform based on cognition

2.2 脉间相位编码信号形式

本文在NRWF基础上提出一种脉间相位编码信号来抑制距离折叠扩展杂波,因此先对NRWF进行简要介绍,示意图如图3所示。

NRWF如下所示:

(8)

式中,Cn为脉间相位码;up(t)为单个线性调频脉冲信号形式。

Cn=πcn2

(9)

(10)

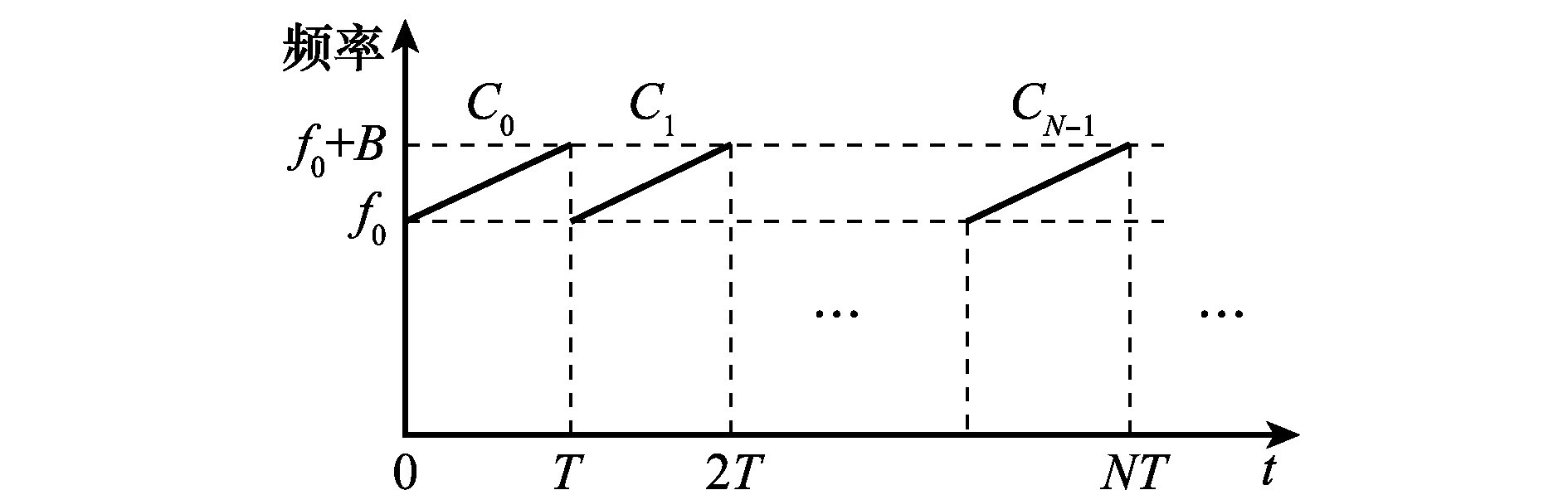
图3 NRWF示意图Fig.3 Diagram of NRWF

考虑如下场景:当处理第m个波形时,第m-l个发射波形对应的回波经l次距离折叠进入雷达接收机和第m个波形进行处理。

(11)

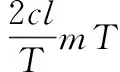
图4给出了发射NRWF回波无模糊与回波一次折叠情况,无模糊回波Dechirp处理后脉间相位码完全抵消,模糊回波Dechirp处理后脉间相位码产生相位差,如式(11)所示。

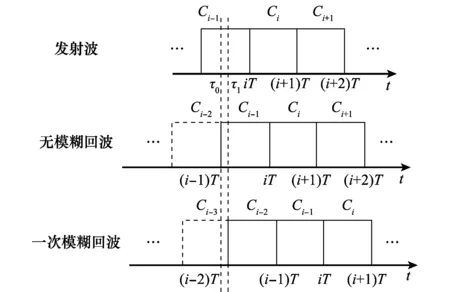
图4 NRWF回波情况Fig.4 Echo circumstances of NRWF

非并发波形可使折叠杂波在频谱上搬移到指定位置,改善了低速目标检测质量,但扩展杂波依旧存在,牺牲了其他有用多普勒检测区域。

针对非并发波形存在问题,本文在其基础上提出一种脉间相位编码波形,波形示意图如图5所示,波形可表示如下:

(12)

式中,A为振幅;Ψn为脉间相位码;up(t)为单个线性调频脉冲信号表示。

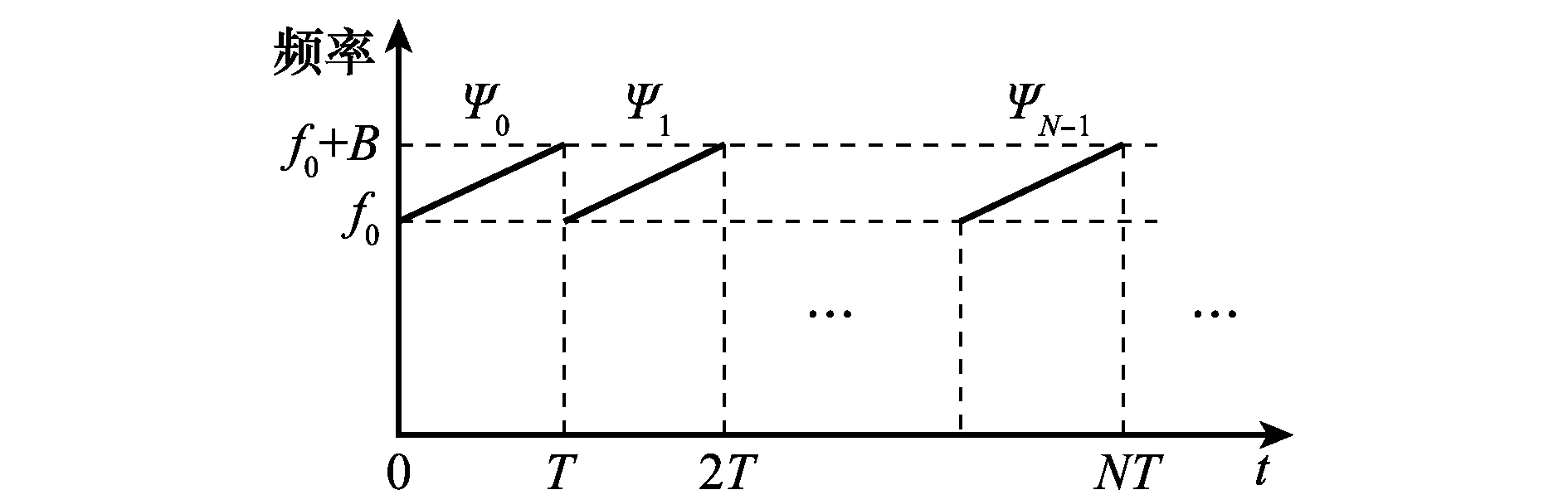
图5 脉间相位编码波形示意图Fig.5 Diagram of the inter-pulse phase coded waveform

考虑如下场景:当处理第m个波形时,第m-l个发射波形对应的回波经l次距离折叠进入雷达接收机和第m个波形进行处理。

脉间相位码Ψn为

(13)

(14)

当l=0时,即回波无距离模糊,Δθ0=0,即脉间相位码对回波处理无影响。

当l≠0时,即回波距离模糊,Δθ0≠0,即脉间相位码对回波处理产生影响,式(14)多项式第一项为常数项,可忽略,第二项为线性项,可通过设计参数b1使折叠杂波搬移到频谱上指定位置,剩余项为非线性项,可通过设计参数用于补偿电离层相位污染函数,使杂波压缩,从而实现折叠杂波在频谱上搬移到指定位置的同时,减少杂波淹没的检测区域。

回波无模糊与一次模糊情况如图6所示。

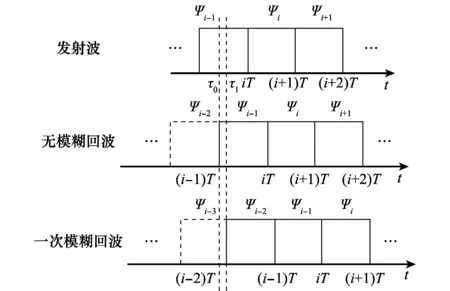
图6 脉间相位编码波形回波情况Fig.6 Echo Circumstances of the inter-pulse phase coded waveform

2.3 脉间相位码设计

第2.2节给出了脉间相位编码信号信号形式,本文主要给出这一信号脉间相位码的求解方法,第2.1节中扩展杂波相位污染函数提取方法在文献[1-2]中已有详细介绍,本文不进行具体讨论,默认已经获得。

为便于脉间相位码设计,需要将已获得的预测相位污染函数表示为多项式和的形式,因此需要确定相位污染函数分解成的多项式阶数以及多项式系数。

本文利用最小二乘法曲线拟合原理来确定电离层相位污染函数阶数与系数,步骤如下。

步骤1首先将污染函数分解为k阶多项式的和,其表达式为

(15)

这个等式可表示为矩阵形式:

(16)

式(16)中范德蒙矩阵记为A,多项式系数组成的矩阵记为D,不同时刻的污染函数记为m,则式(16)可简化为AD=m,其中,A∈RN×(k+1),D∈R(k+1)×1,m∈RN×1。

则多项式系数可通过下式求解:

(17)

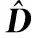
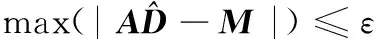
(18)

式中,ε为设定好的误差值。

为了使式(14)中脉间相位码处理后产生的相位差Δθl可以补偿预测的污染函数Mpre(t),需要获得杂波折叠次数m。由于本文重点介绍信号脉间相位码的求解方法,因此只能在此简要介绍一种获取扩展杂波折叠次数m的方法。如图7所示,通过轮流发射两个载频不同,相位旋转因子不同,其余参数相同的NRWF信号,其中Δf≥2B,且Δf+2B≪f0,图中记Δf=2B,Cn与Dn分别为两个NRWF信号脉间相位旋转因子。将回波分别与图8中两种波形进行Dechirp处理,通过滤波从回波中分离出两种信号,并对分离出的信号分别进行多普勒处理,通过比较处理后折叠扩展杂波在频谱上偏移量,结合NRWF脉间相位码参数,可得到折叠扩展杂波折叠次数。

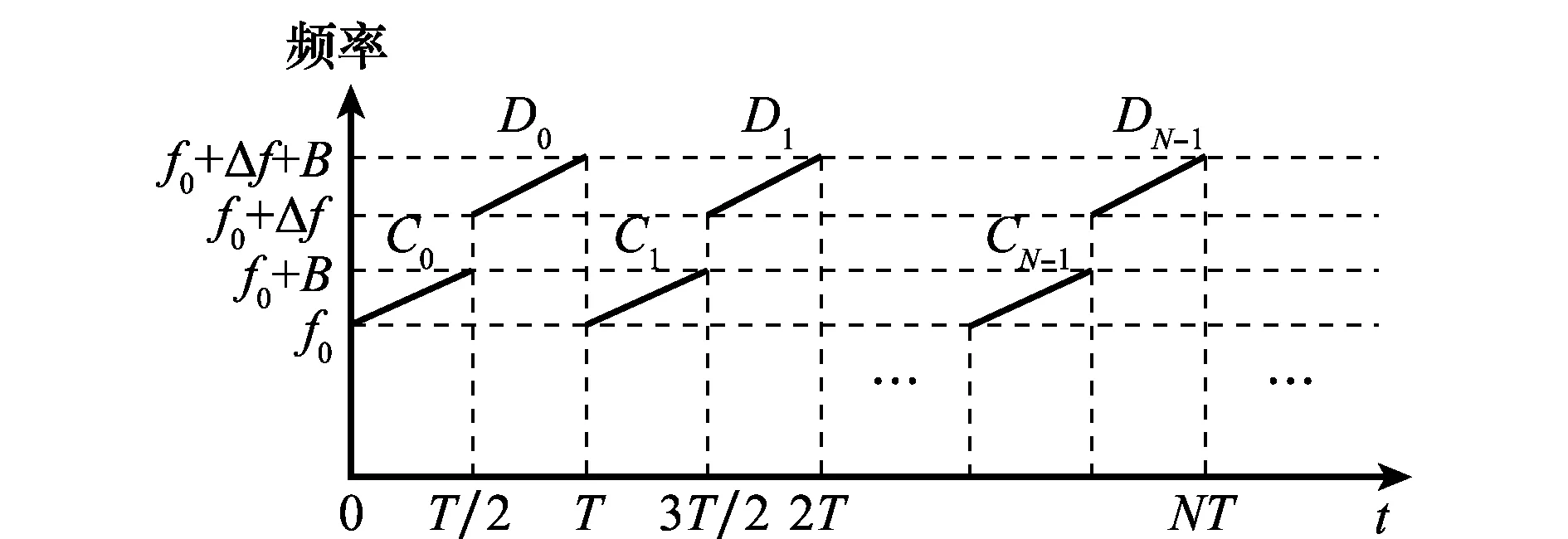
图7 发射波形Fig.7 Emission waveform

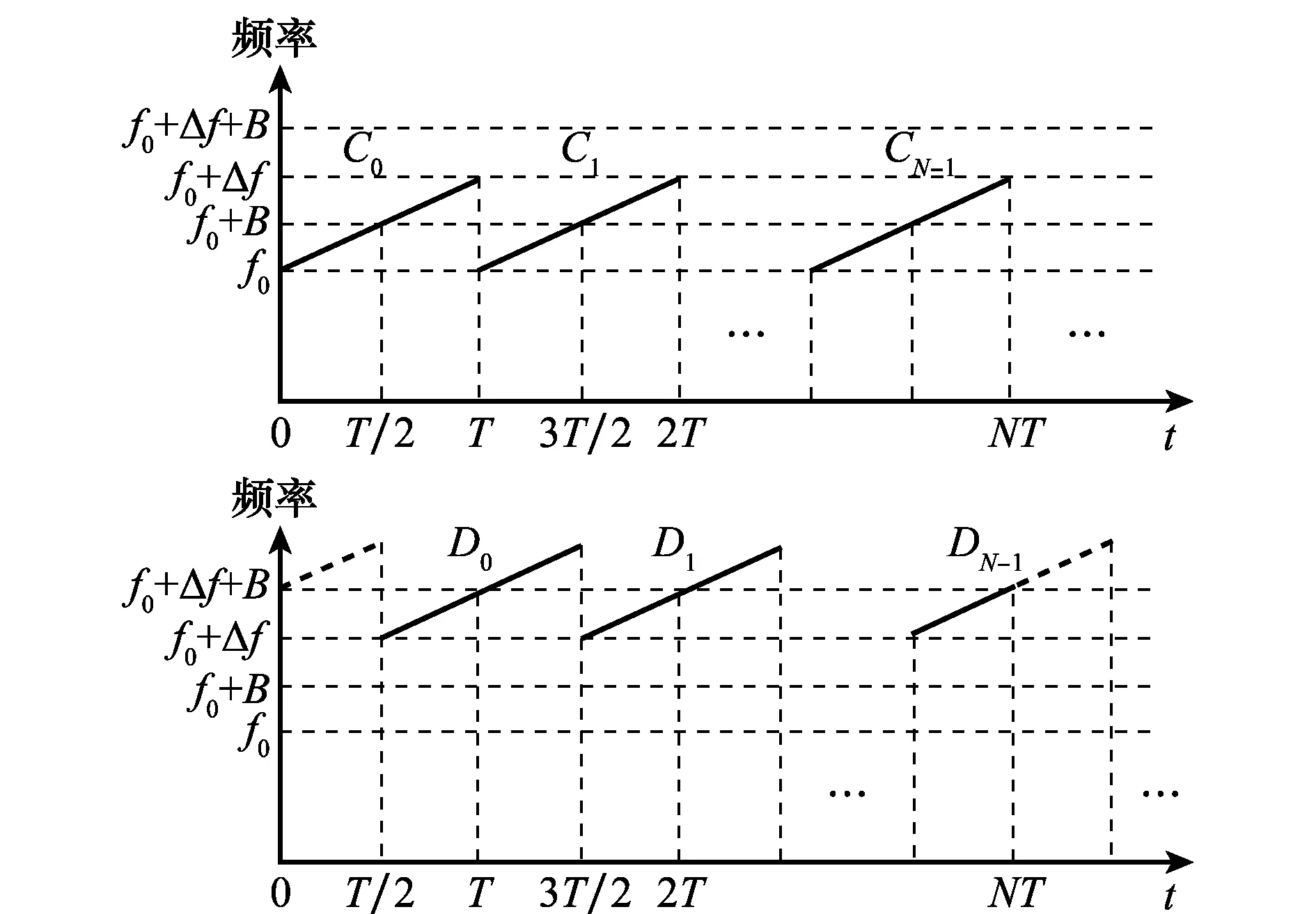
图8 Dechirp处理Fig.8 Dechirp processing

记预测的污染函数Mpre(t)分解为p阶多项式,则设计的脉间相位码为p+1阶多项式的和,使其满足下式。

(19)

即通过预测的污染函数分解出的多项式系数与扩展杂波折叠次数来设计脉间相位码。

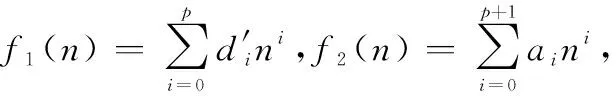
f2(n+m)-f2(n)≡f1(n)

(20)

f2(n+m)可通过组合数展开:

(21)

⋮

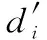
(22)

式(22)可表示为矩阵形式:

(23)

脉间相位码多项式系数可通过式(23)求得。

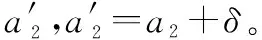
(24)

当然,多普勒区域找不到一小块无目标区域来“安置”压窄的杂波的情况也可能存在,在此可参照上文介绍的杂波折叠次数的获取方法,通过轮流发射两个载频不同,二次相位不同,更高次相位及其余参数相同的脉间相位编码信号,对回波处理,分开两个信号分别做传统距离多普勒处理,折叠扩展杂波被压窄并且分别被搬移到不同多普勒区域,通过比较两个信号距离多普勒图,可等效实现折叠扩展杂波的完全抑制,这一方法核心思想与前文介绍相位编码信号完全相同,故不再展开介绍。

通过上述分析可知,合理设计脉间相位码,可实现扩展杂波的压缩,并将杂波搬移到频谱上指定无目标区域,大大改善目标检测性能。

3 波形稳健性理论分析

预测的污染函数Mpre(t)与实际电离层污染函数不会完全一致,存在一定误差,本节以正弦函数作为污染函数讨论两种产生误差情况。

如图9所示,当预测的相位污染函数与实际电离层污染函数时间上不一致,导致电离层相位污染函数不能完全被补偿,扩展杂波不能被完全压窄,依旧有一定展宽。

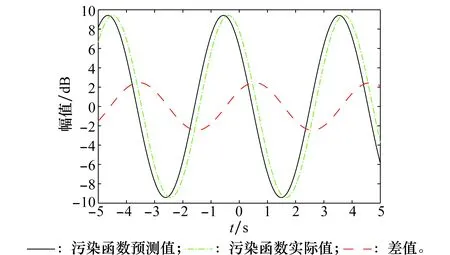
图9 相位污染函数时间预测误差Fig.9 Phase contamination function time prediction error

在这种情况下,预测误差依旧为一正弦函数,如式(25)所示。

ΔMpre(t)=Mpre(t)-M(t)=

asin(w0t+θ+Ψ)-asin(w0t+θ)=

(25)

(26)

式中,Ψ为时间不一致产生的相位差,可表示为Ψ=w0mT,m为实数。

由式(25)可知,当cos(Ψ)>0.5时,扩展杂波被压缩,为使杂波至少压缩为原宽度四分之一,则需满足:

(27)

由上文已知电离层相位污染函数是慢变函数,即w0为一较小值,则预测的相位污染函数与实际电离层污染函数在时间上存在一定误差,扩展杂波依旧能被大幅度压缩。

第二种情况如图10所示,预测的污染函数Mpre(t)数值与实际电离层污染函数存在误差。

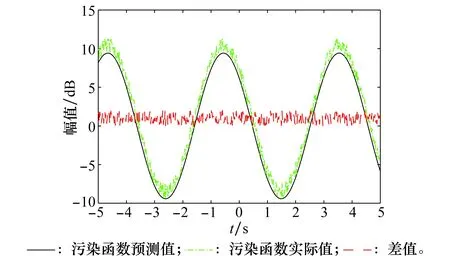
图10 相位污染函数数值预测误差Fig.10 Phase contamination function numerical prediction error

这种情况预测的污染函数Mpre(t)与实际电离层污染函数误差可看作随机量,其会导致回波处理后的信杂噪比变差,变差程度可由误差随机量方差衡量。随机量方差较小时,对结果影响可忽略,当方差较大时,会使回波处理后信杂噪比变差。当预测污染函数Mpre(t)较准确时,则误差值与相位污染函数Mpre(t)相比较小,即信杂噪比性能下降程度可接受。

为使预测的污染函数Mpre(t)更准确,认知雷达对回波信号采用滑窗处理方法,如图11所示,N为脉冲积累数,图中为表示方便,每次处理只滑动一个脉冲,实际中要将污染函数预测准确度与认知雷达工作效率综合考虑来确定滑动脉冲数。

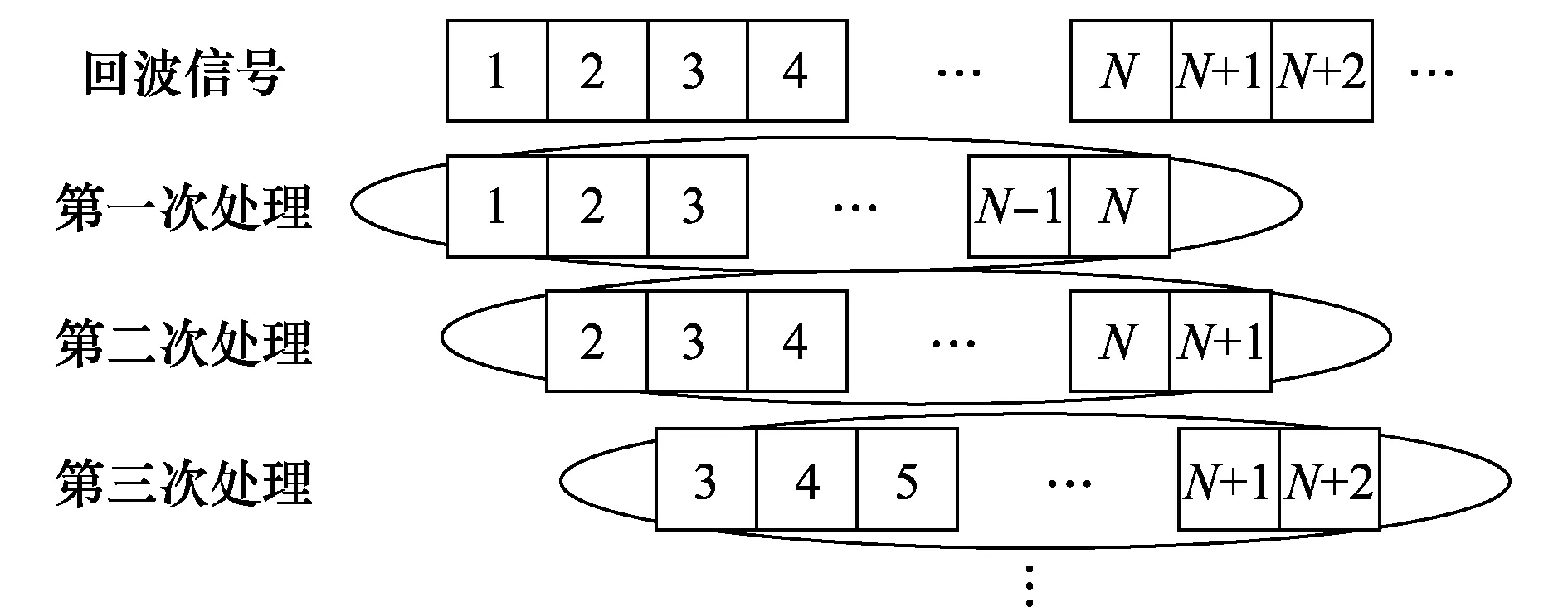
图11 滑窗处理方法Fig.11 Sliding window approach

4 仿真与结果分析

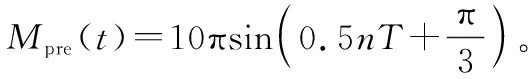
由图12所示,当发射信号为传统线性调频连续波信号,一次折叠扩展杂波淹没低速目标,导致低速目标无法正确检测。图13为发射信号为NRWF时,折叠杂波被搬移到高多普勒频谱区域,实现低速目标正确检测,但高速目标被扩展杂波淹没。

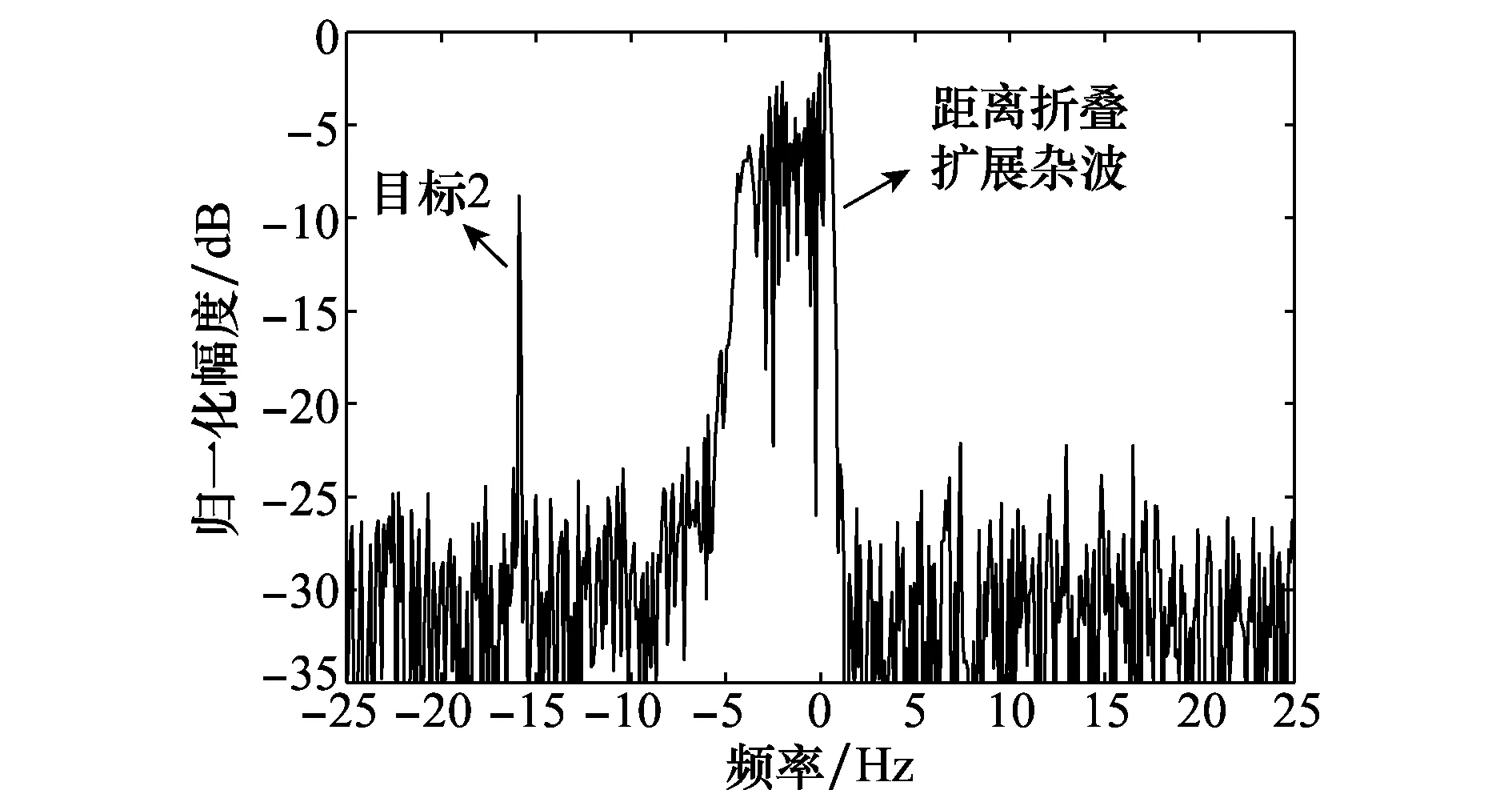
图12 折叠扩展杂波淹没低速目标Fig.12 Folded spread clutter submerges low-velocity target

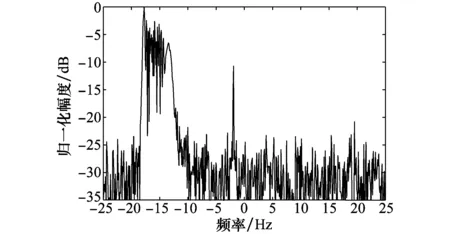
图13 扩展折叠杂波淹没高速目标Fig.13 Folded spread clutter submerges high-velocity target

在非并发波形基础上,本文提出一种基于认知的脉间相位编码信号,由图14所示,当发射这种波形时,回波处理后杂波已压缩,且可搬移到指定位置,实现杂波与目标信号在频谱上分离。由于本文波形作用于强距离折叠扩展杂波,可将相应杂波成分与被其淹没的目标成分分离,改善信杂比,而目标信噪比的改善只能通过传统距离多普勒处理实现。

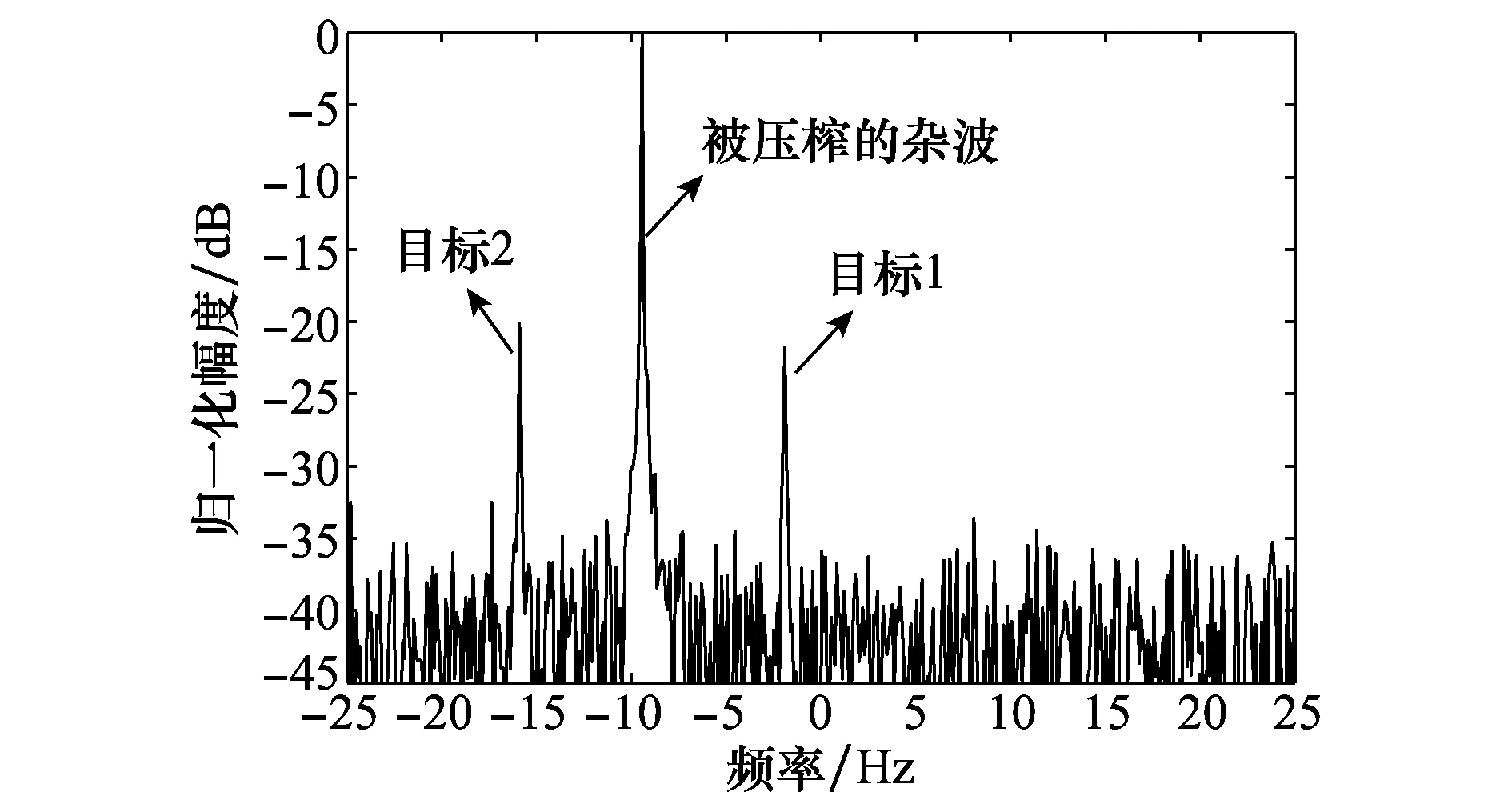
图14 扩展折叠杂波被压缩Fig.14 Folded spread clutter is compressed

在表1中给出了用多项式对电离层相位污染函数拟合的阶数与拟合误差,表2对传统LFM信号,NRWF与本文所提的基于认知的脉间相位编码信号分别进行仿真,目标参数与杂波参数与上述仿真实验相同,分别得到3种波形距离多普勒处理后目标1目标2的信杂噪比,通过对比,本文所提的波形明显优于前两种波形。

表1 相位污染函数拟合结果

表2 仿真结果

如图15所示,当预测的相位污染函数与实际电离层污染函数时间上不一致,延迟12个脉冲周期,与图11中杂波原展宽宽度6.1 Hz相比,杂波宽度被压缩至1.1 Hz,杂波依旧被有效压缩。

如图16所示,当预测的污染函数Mpre(t)数值与实际电离层污染函数存在随机误差时,通过50次蒙特卡罗实验得到不同方差随机扰动与信杂噪比对应关系,此处计算的是目标2的信杂噪比,目标1的对应关系与目标2有相同趋势。当预测的污染函数Mpre(t)数值与实际电离层污染函数存在随机误差量方差较小时,本文介绍的波形对信杂噪比的改善能力远大于误差产生的影响,且可通过认知雷达对回波信号滑动处理方式实时调整波形参数,使随机误差量方差保持在较小值。

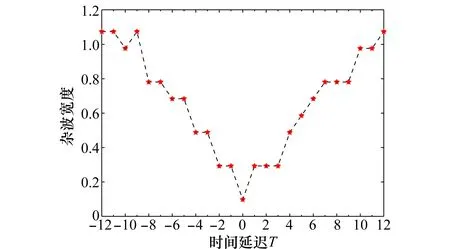
图15 预测时间不一致影响Fig.15 Effect of time prediction error

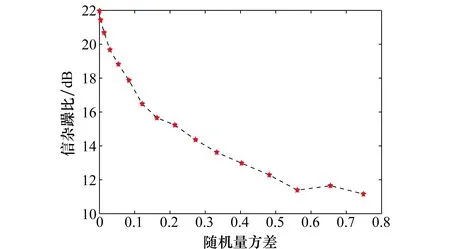
图16 随机误差量影响Fig.16 Effect of random error

5 结 论

本文提出了一种基于认知的脉间相位编码信号来抑制距离折叠扩展杂波。通过与NRWF波形比较,本文提出方法在不牺牲多普勒检测区域情况下,能有效抑制折叠杂波,并且引入认知的思想对波形参数实时更新来适应非平稳的电离层环境。本文波形适用于任何距离折叠,同时相位存在非线性干扰导致展宽的杂波。当然该方法存在一定局限性,这种波形适用于电离层环境变化不过于剧烈情况下工作。仿真实验验证了本文提出波形可以有效抑制距离折叠扩展杂波,改善了目标检测性能。