基于动态规划-遗传算法的防空部署优化模型

颜培远, 刘 曙, 王 君

(空军工程大学防空反导学院, 陕西 西安 710051)

0 引 言

在防空作战领域,防空部署方案优化问题是现代防空研究的热点之一。防空部署方案的优劣直接决定作战效能的高低。目前，国内的研究多是把部署优化问题变成非线性优化问题。文献[1]建立了以掩护价值为目标函数的区城防空优化部署模型,提出一种启发式方法解决部署优化问题;文献[2]提出了一种基于风险决策的区域防空部署方案优选方法,适于快速进行决策的场合;文献[3]将改进的模糊层次分析法应用于弹炮混编防空群机动部署方案的优化与评估,但使用中还需考虑更实际的因素；文献[4]建立了混编群兵力部署优化模型,提出了一种改进的粒子群算法,但还需要提高优化精度;文献[5]提出使用并行改进遗传算法求解组合优化问题,克服了编码时的缺点,提高了搜索速度和解的质量。

以上文献都是在防御方的角度考虑部署优化问题。但是单纯地从防御方的角度考虑部署优化问题,而完全忽略进攻方可能采取的进袭航线,未必是防空问题研究的理想模式。在进攻方实施空袭的过程中,由于兵器性能、防御方雷达主动搜索等客观条件限制,通常会“智能”地选择受雷达照射最少的路径,即选择防御方部署方案中薄弱环节最少的方案。因此,部署优化问题中,充分考虑进攻方的影响是有必要的。本文从进攻方的角度对影响要地防空部署的主要因素[6-9]进行分析,假设进攻方是智能的,能够选择危险最小的航线进攻。由于遗传算法能够较好地解决组合优化问题[10-12],本文提出一种将动态规划算法[13]与遗传算法相结合的防空部署优化模型,将智能算法与非智能算法相结合,对要地防空部署进行优化,取得了较理想的结果。

1 影响要地防空部署的主要因素

1.1 防空武器的类型、数量和性能

防空武器的作战效能主要受雷达的覆盖范围、导弹杀伤区和单发杀伤概率的影响[14]。雷达的覆盖范围越大,越有利于探测和跟踪空袭兵器。防空武器的杀伤区远界和近界是一条闭合的曲线,杀伤区越大,空袭兵器的拦截范围越大,掩护同样区域,需要的防空武器数量就越少。同时,杀伤区还与空袭兵器的类型和飞行特性、雷达散射面积、干扰性能等有关。图1所示为某型飞机以某一固定速度接近某型防空武器时杀伤概率分布情况。当杀伤区域重叠时,同一区域重叠杀伤区域数目越高,目标杀伤概率越高,防空效果越好。

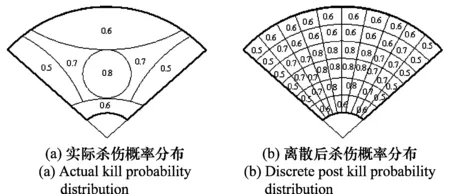
图1 地空导弹杀伤区杀伤概率分布Fig.1 Probability distribution of killing zone of ground to air missile

1.2 地理特征

地理特征有地形地貌、水系、地物等[15]。防空武器的部署受地形起伏的影响。首先,高山等地形可以遮蔽雷达的“视线”,使雷达不能探测、跟踪遮蔽高度以下的空袭兵器;其次,防空武器阵地应尽量平坦,而且避开湖泊、林地、居民区等。

地形对雷达视线的遮蔽如下所示:以海平面为基准面,设雷达天线高于地面,由图2可见,雷达能探测(跟踪)的目标最小高度htmin为

htmin=(O′T′tanεV+hR)-ha

(1)

式中,O′T′表示雷达与空袭兵器的水平距离;hR表示雷达天线的海拔高度;ha表示空袭兵器在地面投影点的海拔高度;εV表示雷达对空袭兵器观测角。

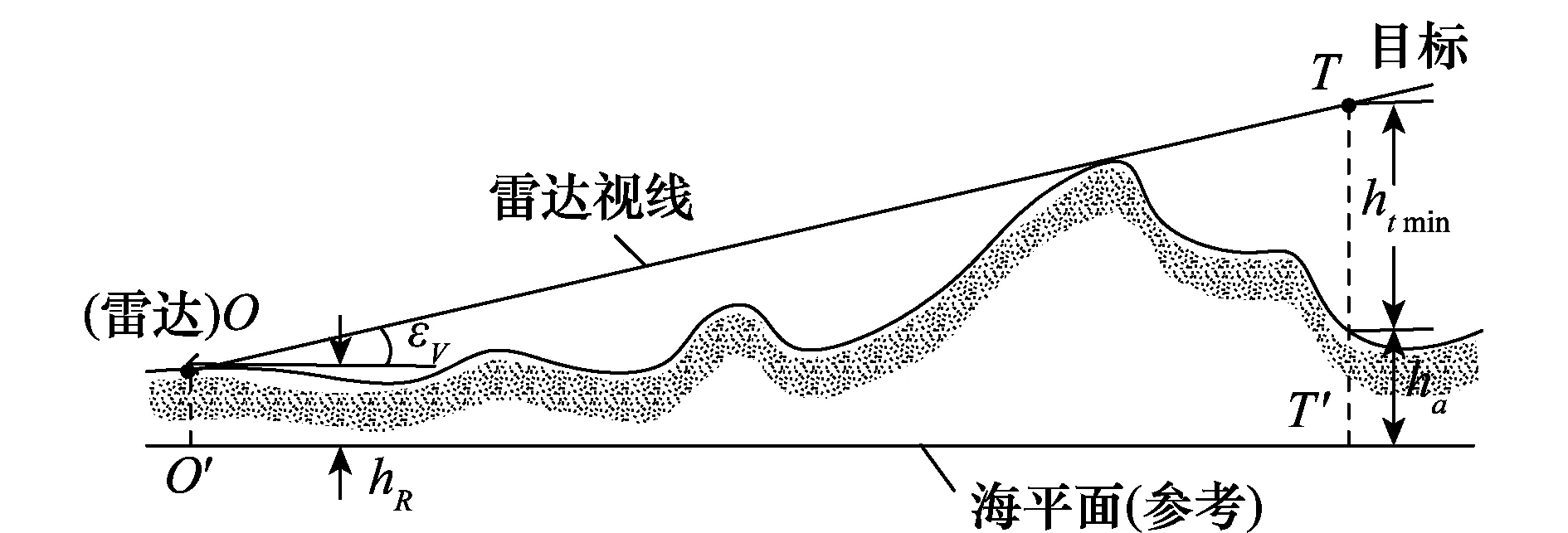
图2 地形对雷达视线遮蔽情况示意图Fig.2 Sketch map of the terrain to the radar line of sight

为有效地探测和拦截空袭兵器,雷达都需要在一定范围内规定最小的遮蔽角εVmin,确定部署点时,雷达对目标观测角必须满足:

εV<εVmin

(2)

1.3 被掩护对象的性质和面积

在空袭时,进攻方总会选择具有较高作战价值的关键目标进行打击,如重要的交通枢纽、指挥中心和防空阵地。因此,要重点针对这些关键目标进行防空武器部署,防止兵力分散,降低防御效能。

按照目前世界防空学说,一般将被掩护对象分为3类:战略性、作战性和战术性被掩护对象。确定被掩护对象的边界线时,要对被掩护对象的性质、面积、形状等综合分析,对被掩护对象的重要度进行量化。当保卫多个相邻掩护对象时,根据上级意图和被掩护对象的具体情况划定边界线。只有科学合理地确定被掩护对象的范围,才能集中力量确保其不受损失或减少损失,以满足高技术条件下空袭的特点,提高防御效能。

2 要地防空部署优化模型

2.1 基本概念描述

根据影响防空部署诸多因素,要地防空部署优化模型的建模思路是:先确定若干个武器的部署区域(由上级确定),然后在每个区域内选择一个适合部署的阵地进行武器部署,从而形成一套部署方案[16]。由于每个武器部署区域都有很多阵地,可供选择,因此会产生多套部署方案。优化时,假设进攻方足够“智能”,能够知悉防御方武器配置,可以选择一条最优的进攻路径,即使用动态规划-遗传算法可以找到部署方案防守最薄弱的一条路径,继而找到最优部署方案,如图3所示。

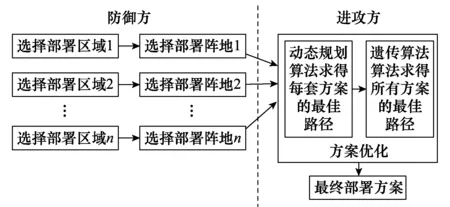
图3 建模思路示意图Fig.3 Sketch map of modeling ideas

可以看出,这是一个求防空武器和部署阵地之间组合的优化问题。本文将遗传算法与动态规划算法相结合,从大量部署形式中选出最优方案,从而确定防空武器的数量和最佳部署形式。

定义1易受攻击区(vulnerable zone,VZ):空袭兵器投弹或发射空地导弹时,距要地的可能最远位置线,称为空袭兵器的投弹线。这条投弹线是一条闭合曲线,为保证要地的安全,应将空袭兵器在投弹前或发射空地导弹前杀伤。空袭兵器的投弹线以及其内部区域共同构成VZ,其中,空袭兵器的投弹线是VZ的边界。如图4所示。

定义2危险区(danger zone,DZ):空袭兵器在飞向VZ过程中,可被远程预警雷达(CSR)或跟踪制导雷达可发现并跟踪的区域,远程预警雷达和所有跟踪制导雷达所覆盖区域的边界称为DZ边界。如图4所示。

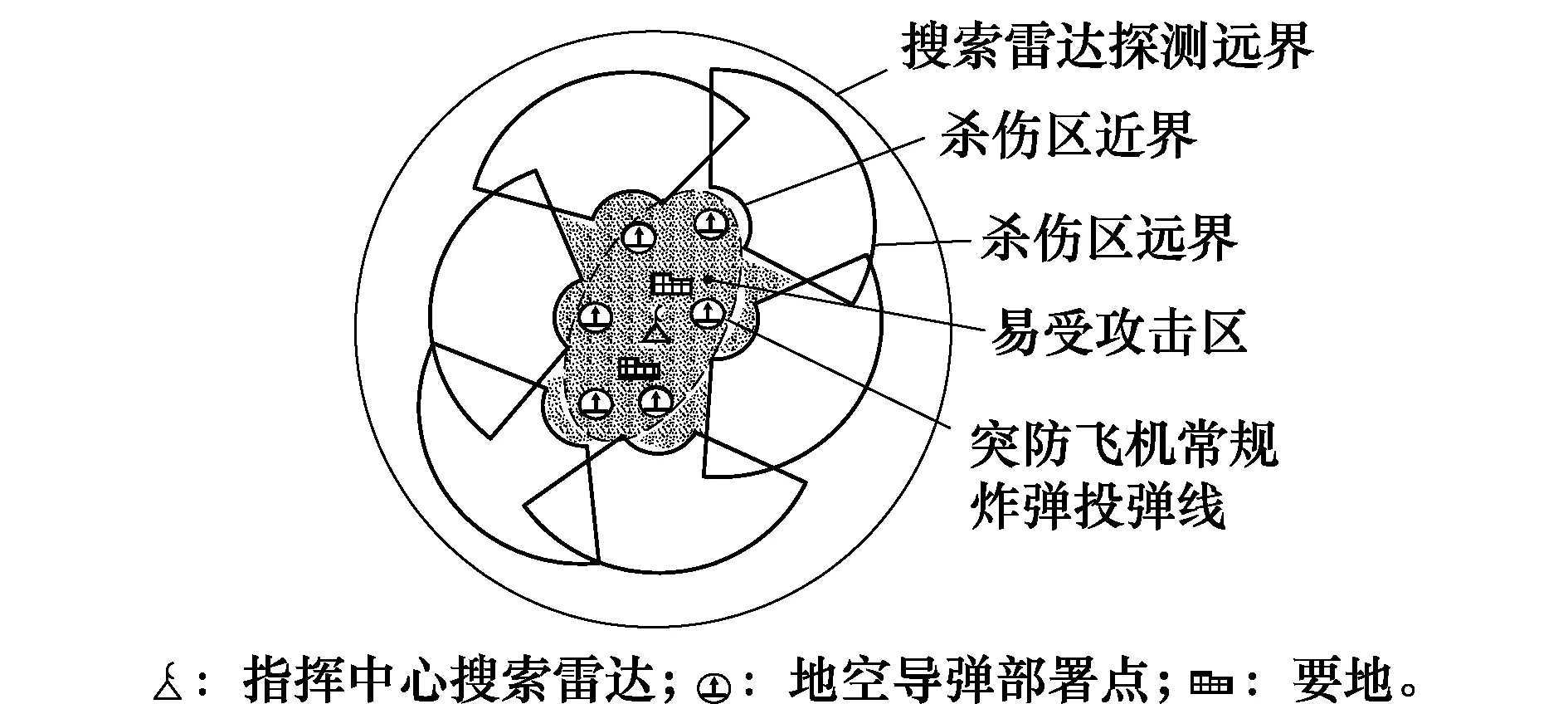
图4 防空武器系统的不同区域Fig.4 Different areas of air defense weapon system

定义3杀伤区(kill zone,KZ):由所有防空武器的KZ组合而成的区域。如图4所示,在一个防空系统中,KZ边界是一条闭合曲线。防空武器的KZ应处于DZ(雷达的探测跟踪区域)之内,VZ应处于KZ之内。

2.2 部署优化模型建立

定义4设空袭兵器选择从DZ边界到VZ边界的进袭航线中,将面临防空武器的拦截危险,地域特征、防空武器杀伤概率分布、空袭兵器的飞行时间等都将影响航线上所面临危险的大小。每种部署方案必有一条或多条航线,使空袭兵器遇到的危险最小,这个最小危险值可用来确定部署形式的防空效能,即防御方需要找到一种部署形式,使防御的整体有效性最大。为此,将航线上空袭兵器面临的危险在一定条件下进行量化,该量化在二维空间中展开,用水平线和垂直线构成一系列一定大小的方格[17-18],如图5所示,方格的大小由地形的粒度决定。这样,空袭兵器从DZ边界到VZ边界,其航线要经过一系列小方格,每一个小方格与一个经验危险值相关,称之为防空系统对目标所造成的危险指数(danger index,DI),防空系统对空袭兵器航线上产生的危险指数总和,称为累积危险指数(cumulative danger index,CDI),它由航线经过的所有小方格的危险指数相加得到。

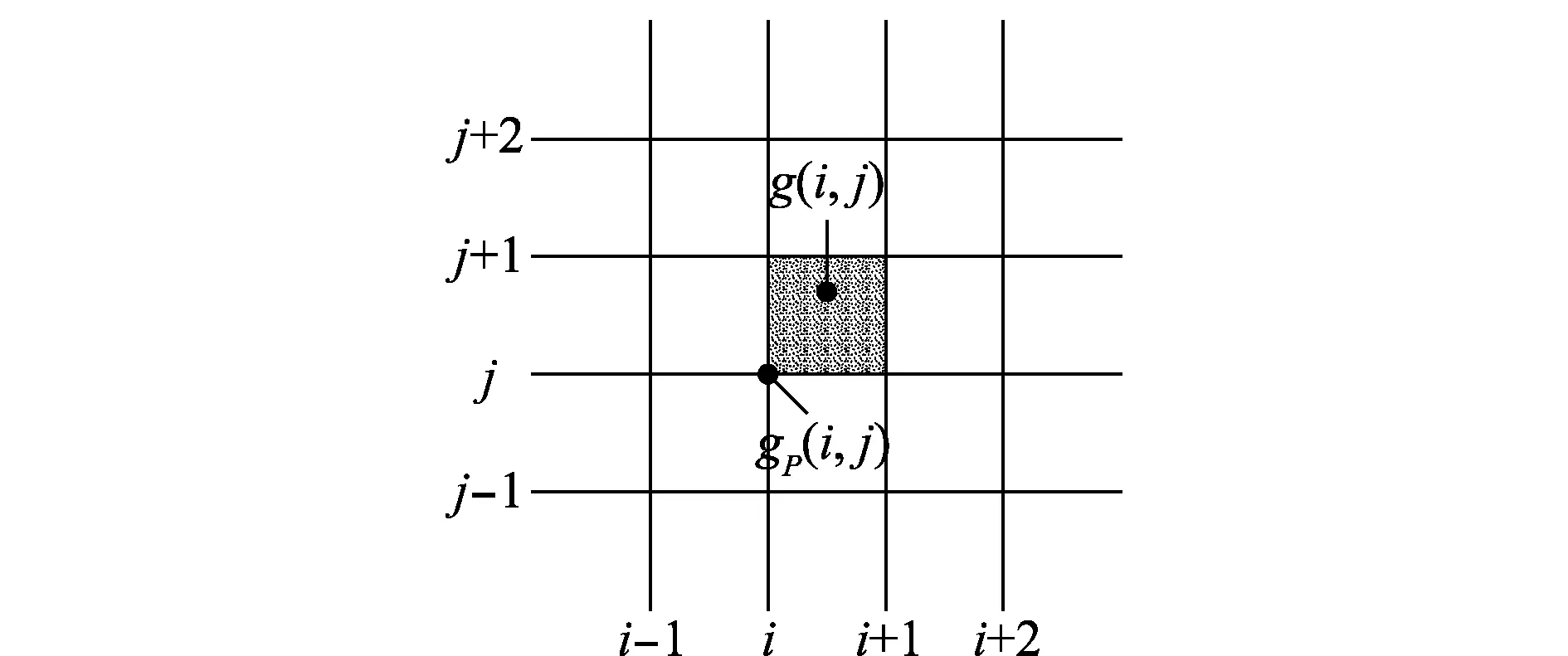
图5 方格标识Fig.5 Square identification

部署形式的集合记为P,给定一种部署形式p(p∈P)下,目标某一可行航线记为r,可行航线集合记为R(p),则目标函数可表示为

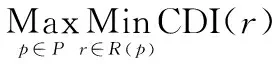
(3)

认为空袭兵器从DZ边界上某点处进袭,从此点向前,有多条到达VZ边界的航线可供选择[19],每条航线都有累积危险指数,累积危险指数最小的航线即为最优航线,称为局部最小累积危险指数(local minimum cumulative danger index,LMCDI),它与组成DZ边界的每一个方格相关。所有的局部最小累积危险指数中,最小的称为全局最小累积危险指数(global minimum cumulative danger index,GMCDI)。这样,目标函数可表示为

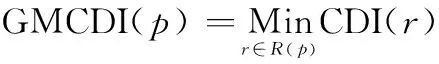
(4)

对于给定的部署形式p∈P,如果DZ边界内全部小方格集合为G(p),则

(5)

式中,R0(g)是对于一个给定DZ边界上的方格g(g∈G(p)),空袭兵器所有可能飞行航线的集合。以这种方式,全局最小累积危险指数也表示为

(6)

局部最小累积危险指数也表示为

(7)

定义5对图5中的小方格g(i,j),给一个可见值Vij(Vij∈[0,1]),它表示了雷达探测和跟踪此方格内空袭兵器的能力。如果此方格不在雷达的探测跟踪范围内或完全被地形遮蔽,则Vij=0;如果雷达可以探测到该方格上任意飞行高度的空袭兵器,则Vij=1。如果该方格位于至少一个KZ内,则分配相应的杀伤概率;如果该方格不被KZ覆盖,相应的杀伤概率为零。杀伤概率表示为Kij,概率分布如图1所示。对某方格g(i,j)的危险指数Dij表示为

Dij=Vij(1+Kij)

(8)

对位于DZ内的空袭兵器,虽然Kij=0,但Vij≠0,则Dij≠0。如果一个方格位于两个KZ的重叠部分,当重叠区内只有一个防空武器(例如,危险指数值最大的防空武器)被分配了射击目标的任务时,较大的一个危险指数可作为与此方格相关联的危险指数;当两个防空武器都指定射击方格内的目标,则此方格的Dij值按下式计算:

Dij=[Vij1+Vij2(1-Vij1)][1+Kij1+Kij2(1-Kij1)]

(9)

式中,Vij1、Vij2分别为防空武器1、2雷达对方格g(i,j)内目标的可见度;Kij1、Kij2分别为防空武器1、2对方格g(i,j)内目标的杀伤概率。

设飞机飞行的最高高度hmax,则方格g(i,j)的可见值为

Vij=Max{0,1-[htmin/(hmax-ha)]}

(10)

将全部方格g(i,j)的高度存于计算机数据库中,该高度由g(i,j)方格4个顶点的高度加权平均得到。

3 要地防空部署优化算法设计

3.1 动态规划算法求解单个方案的最小危险航线

算法的基本思路是,已知部署地区的海拔信息和杀伤概率的分布情况,从进攻方的角度出发,对被掩护对象攻击时必然选择危险性最小的航线。将部署方案中每个方格g(i,j)的危险指数记为Dij,所有二维方格的危险指数矩阵记为D。局部最小累积危险指数矩阵记为L,从方格g(i,j)到VZ边界的局部最小累积危险指数记为Lij。动态规划算法的目标是获得矩阵L,其中优化的初始区域是DZ内的方格的集合,结束区域是VZ边界内的方格的集合。初始化时,VZ内方格的Lij赋值为0,其他方格的Lij赋值为相应的K值。矩阵D、L都是p×q维。每一个方格(i,j)都有一层方格将其包围,该包围方格层记为Eij,即

Eij={(K,L):(i-1)≤k≤(i+1),(j-1)≤l≤

(j+1),1≤k≤p,1≤l≤q,(k,l)≠(i,j)}

(11)

显然,对于一个方格,包围方格层中最多只有8个方格,如果(k,l)∈Eij,则(i,j)∈Ekl。

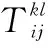
(12)

式中

(13)

当执行到第n步时,在确定此步一个方格的局部最小累积危险指数前,必须先确定哪些方格属于第n步。这里为了缩小计算时间,对动态规划算法进行改进,认为第n步一般是形成第(n-1)步中方格集合的外层包络方格集合。记第n步的方格集合由Sn给出,则动态规划算法的主要步骤如图6所示。

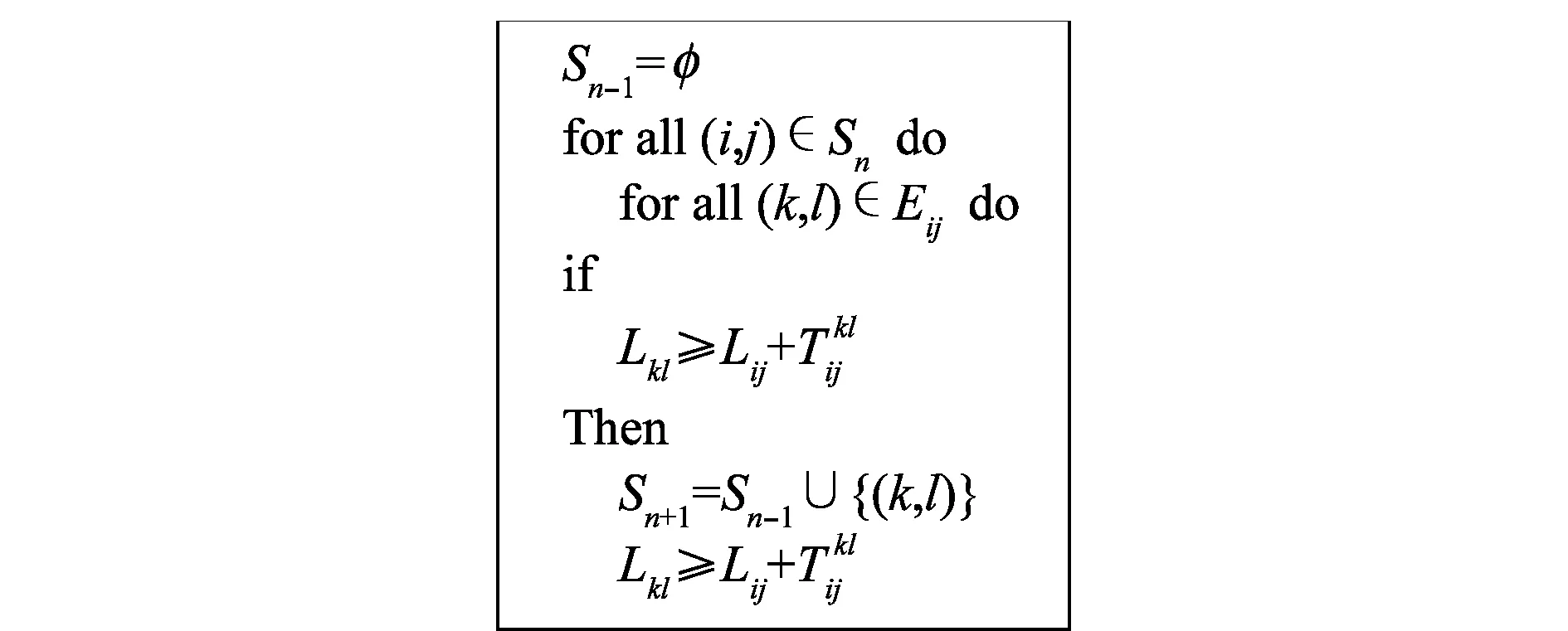
图6 动态规划算法流程Fig.6 Dynamic programming algorithm flow

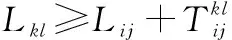
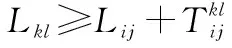
3.2 遗传算法求解单个方案的最小危险航线

3.2.1 遗传算法求解最优部署方案

要地防空部署优化问题的可行解是一组部署方案,包括防空武器类型及确定的精确部署阵地位置[20]。假设要对m套防空武器进行部署(针对单一武器类型),现有m个武器部署的大概地点,每个大概地点附近有n个精确部署阵地,且每个大概地点附近仅选择一个精确部署阵地进行部署,每个阵地仅支持部署一套防空武器。由于武器数目和精确地点数目均为整数,所以采用整数进行编码较为合理。

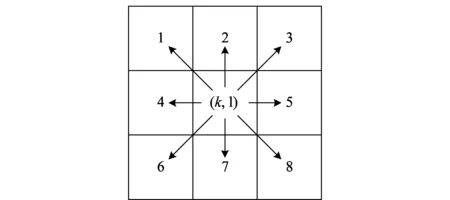
图7 生成最佳航线Fig.7 Generating the best route

编码时,染色体的长度为m,染色体的每一个基因与解的每一维变量相同。优化问题的一个有效解为X=(x1,x2,…,xk,…,xm),其中k为1～m的整数,表示武器部署大概地点的标号,xk为1～n之间的整数,表示武器部署精确地点的标号,xk=1表示防空武器部署在第k个大概地点附近的标号为1的精确地点。

3.2.2 种群初始化

在遗传算法用于种群进化之前,需要建立初始种群。初始种群的选取将直接影响算法搜索全局最优解的能力。这里针对m套防空武器和n个精确部署阵地位置产生初始种群,初始种群的规模应适应于问题的难度[21],假设规模为N。

3.2.3 适应度评价

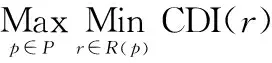
3.2.4 选择算子

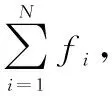
3.2.5 交叉算子

在种群交配时,指定一个交配概率(Pc,一般取0.4～0.99)决定每条染色体是否能进行交配。对于每条染色体产生[0,1]的随机数(用A表示),若A小于Pc,则该染色体进行交配,否则不参与交配,并将其直接复制到新种群中。将Pc选择出来的每两条染色体的部分基因交换,产生两个子代染色体。染色体的交配位置是随机产生的,交换的基因为该位置后的所有基因。新种群规模仍为N。

3.2.6 变异算子

染色体的变异作用于基因上,变异时指定一个变异概率(Pm,一般取0.001～0.1)决定种群中染色体的每一位基因是否进行变异。对于染色体的每一位基因产生[0,1]的随机数(用B表示),若B小于Pm,则该基因进行变异,否则该基因不发生变异。根据染色体的编码,变异的取值为1～n之间的整数。

3.2.7 求解步骤

运行过程如下:

步骤1根据问题确定初始种群的规模N,当前进化代数G=0;

步骤2用适应度函数评价全部染色体,计算各染色体的适应度值,并保存适应度值最大的染色体Best;

步骤3按照轮盘赌选择算法对种群进行选择;

步骤4根据交配概率Pc从种群中选择染色体进行交配操作;

步骤5根据变异概率Pm从种群中选择染色体进行交配操作;

步骤6产生的新种群取代原有种群,并计算新种群中各染色体的适应度值。如果新种群的最大适应度值大于Best的适应度值,则更新Best,用新种群中的最大适应度值对应的染色体代替Best,否则不更新;

步骤7当前进化代数G加1。算法结束条件为Best达到规定要求或G超过最大进化代数,若不满足结束条件,则返回步骤3。

4 算例仿真及分析

4.1 算 例

如图8所示,假设根据上级意图(已确定进攻方的空袭兵器)在保卫要地周围确定5个武器部署的大概地点(1、2、3、4、5),每个大概地点附近规定范围内有5个精确地点可供武器部署,求解针对单一武器类型时的最佳部署形式。

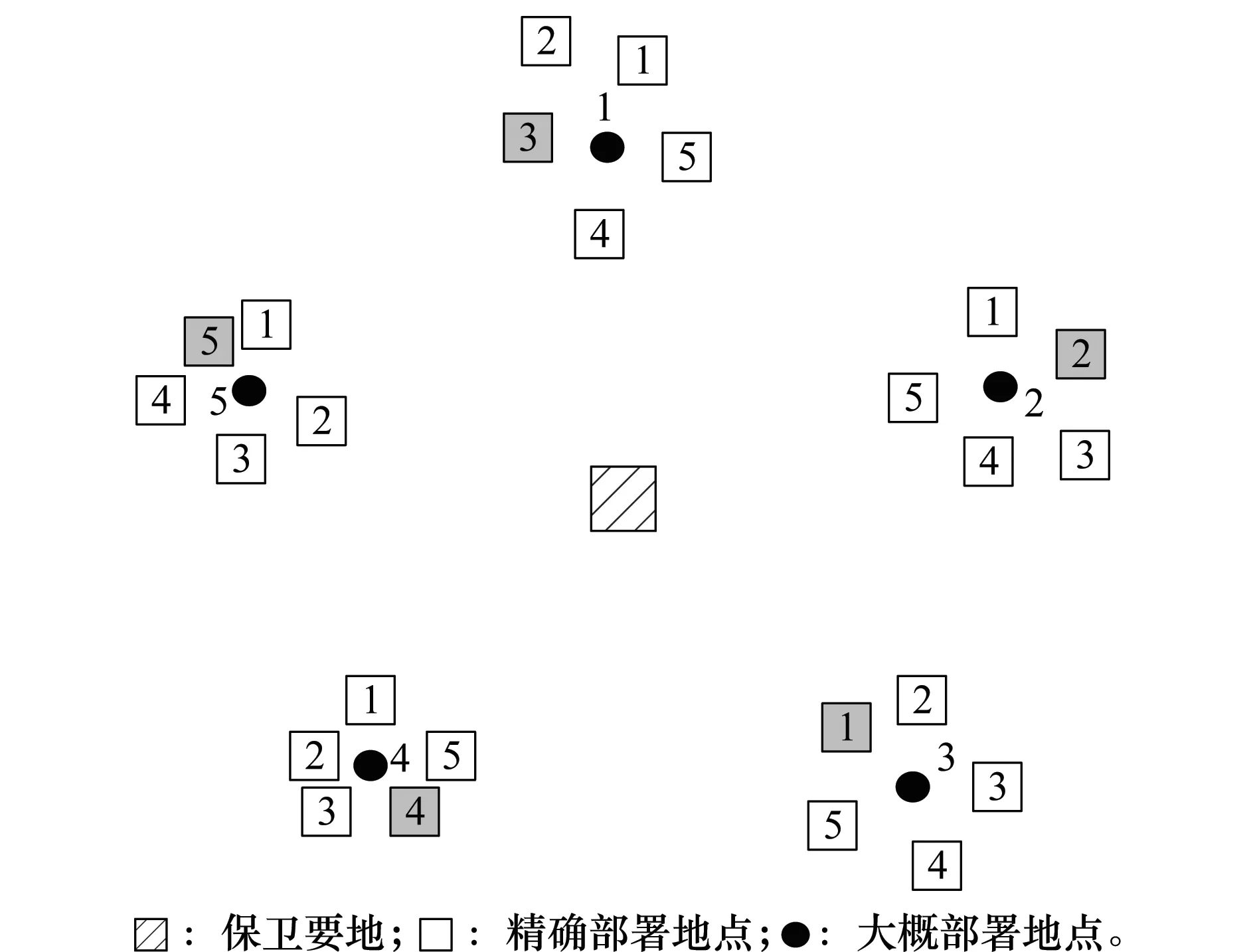
图8 算例示意图Fig.8 Example diagram

4.2 仿真实验及结果分析

仿真实验使用Matlab2013软件进行,遗传算法中相关参数设置如下:种群规模为N=100,最大进化代数为1 000,交配概率Pc=0.95,变异概率Pm=0.1。

根据算例对染色体进行编码,有效解为X=(x1,x2,x3,x4,x5),其中xi=1,2,3,4,5(i=1,2,3,4,5)。然后生成初始种群,计算每条染色体的适应度值,如表1所示。

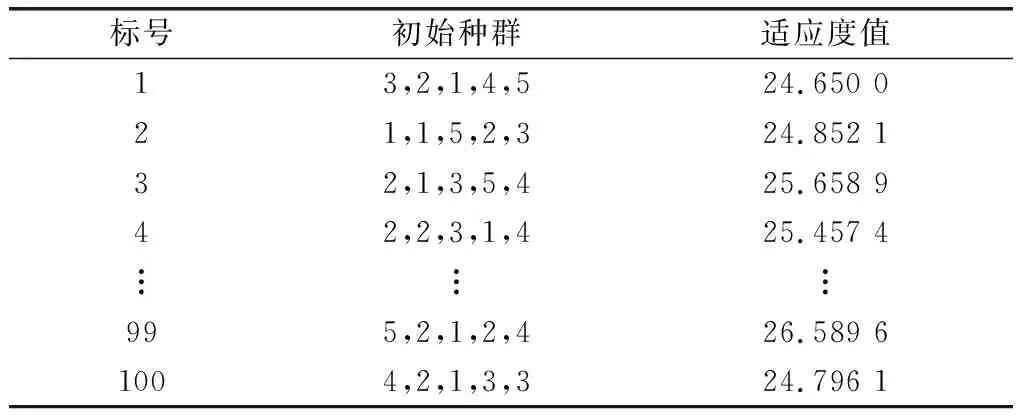
表1 初始种群及适应度值

仿真实验的目标是求出适应度值最大的种群,下面仅对1号染色体(3、2、1、4、5;如图8中阴影所示)的适应度值求解过程进行说明,其余染色体适应度值的求解与1号染色体相同。根据定义1～7及部署方案,假定将整个区域离散成50×50的二维方格,每个方格的边长为10 km。确定DZ、KZ、VZ以及相应高程的数据,经计算得到如图9所示的危险指数矩阵D(50×50),图中用颜色区分危险指数的不同。

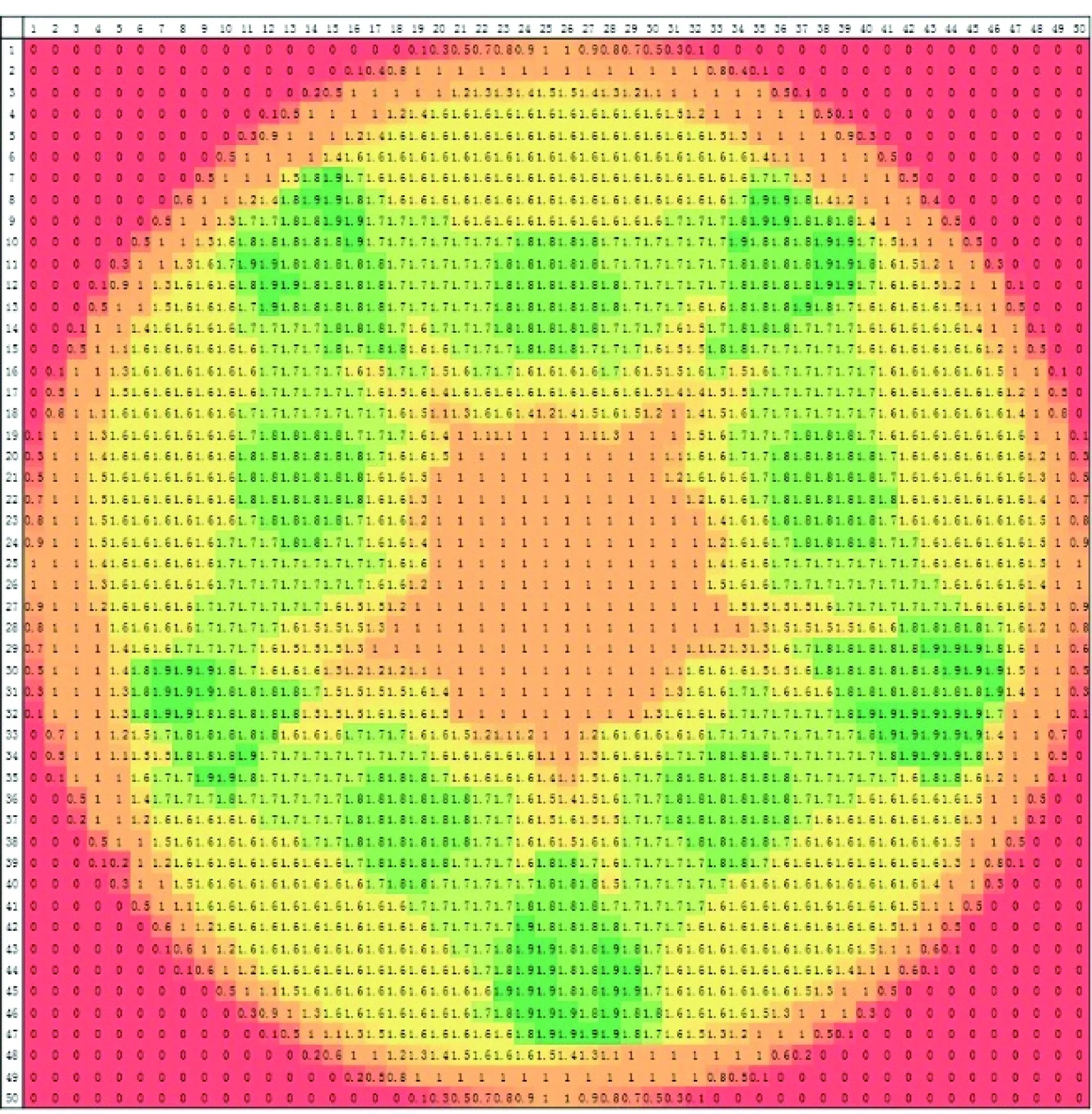
图9 危险指数矩阵DFig.9 Risk index matrix D

将矩阵D代入动态规划算法程序中运行,得到局部最小累积危险指数矩阵L,如图10所示,图中用颜色区分局部最小累积危险指数的不同。最后得到全局最小累积危险指数为L29,1=22.650 0,即适应度值为22.650 0。同时,也得到了航线矩阵P,如图11所示,图中方格内的数字表示下一步前进的方向。最终该适应度值对应的航线为(29,1)→(29,2)→(29,3)→ (29,4)→(29,5)→(29,6)→(29,7)→(29,8)→(29,9)→(29,10)→(29,11)→(29,12)→(29,13)→(29,14)→(29,15)→(29,16)→(29,17)→(29,18)→(29,19),如图11中黑框所示。

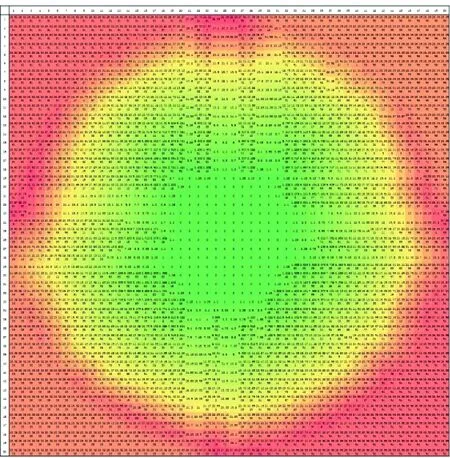
图10 局部最小累积危险指数矩阵LFig.10 Local minimum cumulative hazard index matrix L

图11 航线矩阵PFig.11 Route matrix P

初始种群确定后,运行程序,通过选择、交配、变异,得到Best适应度值为26.731 8,Best适应度值与进化代数的关系如图12所示,进化代数在0～100代时,Best适应度值变化明显,但随着进化代数的增加,适应度逐渐收敛到一个固定值。

最终Best适应度值对应的染色体(5、3、2、1、4)即为最佳部署方案,其对应的最佳航线为(5,39)→(6,39)→(7,39)→(8,38)→(9,37)→(10,36)→(11,35)→(12,34)→(13,33)→(14,32)→(15,32)→(16,31)→(17,31)→(18,31)→(19,30),其中方块(5,39)在DZ边界上,从正方形边界到方块(5,39)的航线,只需保证其经过的每一个方块的危险指数为0即可。通过对算例的仿真实验可以看出,本文所设计的优化模型能够得到基于进攻方的最优部署方案,为指挥人员进行防空武器部署提供参考和决策依据。

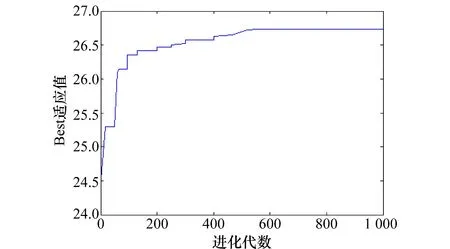
图12 Best适应度值的收敛过程Fig.12 Convergence process of the fitness value of Best

5 结束语

本文以“智能敌人”在进攻时航线上累计危险指数为指标,将动态规划算法与遗传算法相结合,提出的一种基于动态规划-遗传算法的模型,很好地解决了防空部署优化问题。然而,将本文的模型运用于工程实践,还需要考虑更多的影响因素和具体参数设定。由于抗击空袭兵器饱和进攻、电子战设备以及抗击隐身目标等典型作战想定并不是仅仅通过改变部署方式就可以解决的,所以本文并没有提及,下一步会将其重点研究。为了精确地进行防空部署,将二维平面拓展至三维空间将会是下一步的研究方向。