地球同步轨道SAR两维奇异值分解成像方法

游 冬, 孙光才, 李亚超, 陈溅来, 邢孟道

(1. 西安电子科技大学雷达信号处理国家重点实验室, 陕西 西安 710071;2. 西安电子科技大学信息感知技术协同创新中心, 陕西 西安 710071)

0 引 言

星载合成孔径雷达(synthetic aperture radar, SAR)不受光照、气候等条件的影响,具有全天时、全天候、高分辨的工作能力。相对于机载SAR,星载SAR在较高的轨道高度运行,具有更长的连续对地观测时间、更大的观测范围。目前在轨的星载SAR系统均为搭载于低轨卫星上的低轨星载SAR系统(low earth orbit SAR, LEO SAR),其轨道高度低,重访周期长。1978年,Tomiyasu率先提出了地球同步轨道合成孔径雷达(geosynchronous SAR, GEO SAR)的概念,随着轨道高度提升至35768km,GEO SAR具有超大的测绘带宽、仅为1天的重访时间、以及超大的全轨覆盖范围。

由于轨道高度极高,GEOSAR具有超长的合成孔径时间,轨道弯曲不可忽略,还需要考虑地球自转的影响[1-2],卫星运动轨迹为复杂的曲线轨迹,同时测绘带宽度增大,带来了严重的二维空变问题[3-6],对系统参数设计[7-10]及性能分析[11-14]和成像算法设计[15-18]等带来了许多问题。针对GEO SAR长合成时间曲线轨迹,文献[19-22]推导了高阶近似的斜距模型,采用级数反演(method of series reversion, MSR)方法求解了点目标回波二维频谱,其中文献[21-22]在成像过程中没有考虑空变性的影响,仅利用场景中心参考点构造了匹配函数。文献[23]提出了一种在距离频域-方位时域进行二维插值校正距离和方位耦合的方法,并通过非均匀快速傅里叶变换(nonuniform fast fourier transform, NUFFT)来降低计算复杂度。文献[24]针对长合成时间大方位场景方位空变严重的问题,提出了一种级联的SVD -NCS方法校正方位空变。文献[25]针对曲线轨迹提出了一种两步NCS校正方位空变的方法。文献[24-25]提出的NCS方法均通过距离分块消除子块内的距离空变,距离分块方法对于大场景需要相当多的分块,距离处理效率不高。

针对GEO SAR大场景成像存在的严重的二维空变问题,本文提出一种基于两维奇异值分解(singular value decomposition, SVD)的成像方法。首先,基于四次多项式斜距模型,推导得到了二维空变的MSR二维频谱,并将其分解为与距离空变的距离徙动(range cell migration, RCM)校正相关的距离信号和与方位聚焦相关的二维空变的方位信号;然后,利用SVD对距离空变信号进行分解得到距离和多普勒的二维耦合关系,并通过Stolt插值和距离频率重采样完成距离空变的RCM校正;最后,利用级联的SVD-NCS算法完成方位空变校正[24],实现方位聚焦。该方法不需要对空变的MSR二维频谱进行求解得到复杂的处理函数,通过奇异值分解可以简化谱分析的复杂性。

1 GEO SAR信号模型

图1为GEO SAR成像几何模型,为了便于斜距的表示,将星地几何关系在地球固定坐标系下表示。其中,ωe为地球自转角速度,RT(tm)为tm时刻信号发射时的斜距,RR(tm+τ)为信号接收时的斜距,τ为信号发射接收的双程时延,通常情况下τ在0.24 s左右[26],不可忽略;P(X,RB)为场景中任意点目标,P0(X0,R0)为场景中心点。

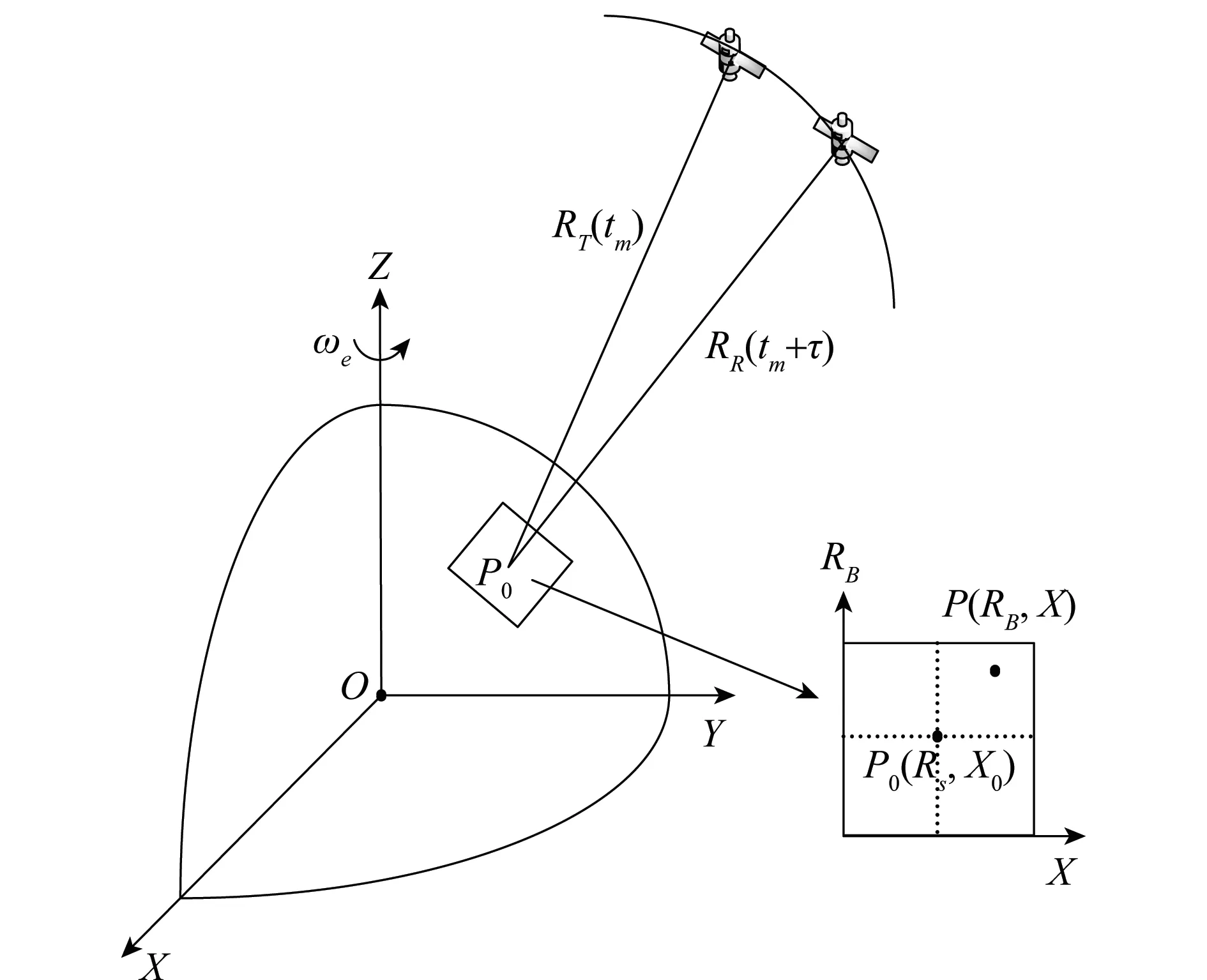
图1 GEO SAR成像几何模型Fig.1 Geometry of GEO SAR imaging system

卫星到场景中点目标P的双程斜距采用4阶多项式斜距模型可以表示为

R(tm;RB,X)=RT(tm;RB,X)+RB(tm;RB,X)=

(1)

式中,ki(RB,X)(i=0～4)为双程斜距的各阶泰勒展开系数。考虑到二维空变高次项的影响,ki(RB,X)应建模为RB和X的二阶多项式模型。

设GEO SAR发射的信号是chirp信号,场景中任意点目标P的基频回波信号为

(2)

式中,R(tm;RB,X)如式(1)所示,为4阶多项式斜距模型；c为光速;γ为发射信号的调频率;λ为载波波长;tr和tm分别为快时间和慢时间;ar(·)和aa(·)分别为线性调频信号距离向和方位向的窗函数。通过驻定相位原理和级数反演法可以得到4阶斜距模型精确的信号的二维频谱表达式,下面给出距离脉压后的点目标P的二维频谱表达式:

S(fr,fa;RB,X)=Ar(fr)Aa(fa-fdc)·

exp(jΦ(fr,fa;RB,X))

(3)

式中,fr和fa分别为距离频率和方位多普勒频率;fdc为多普勒中心频率;相位Φ(fr,fa;RB,X)是文献[22]中推导得到的MSR二维频谱。需要注意的是斜距各阶展开系数ki(i=0～4)均为式(1)中的二维空变系数ki(RB,X)(i=0～4)。根据文献[25],Φ(fr,fa;RB,X)可以分解为

Φ(fr,fa;RB,X)=Φr(fr,RB;fa)+Φa(fa,X;RB)

(4)

式中,Φr(fr,RB;fa)和Φa(fa,X;RB)分别是与距离空变的RCM校正相关的距离信号和与方位聚焦相关的二维空变的方位信号。

2 二维空变SVD特性分析

基于MSR方法求解的二维频谱形式复杂,且该二维谱随距离维和方位维是二维空变的,因此求解各处理函数比较复杂。而奇异值分解可以作为一种高效的数学工具将复杂的二维频谱表示为易于处理的形式。式(5)给出了任一相位矩阵Φ奇异值分解后的表达式[27-28]

Φ=UΣVH=

(5)

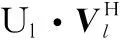
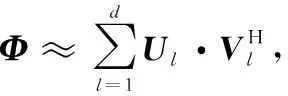
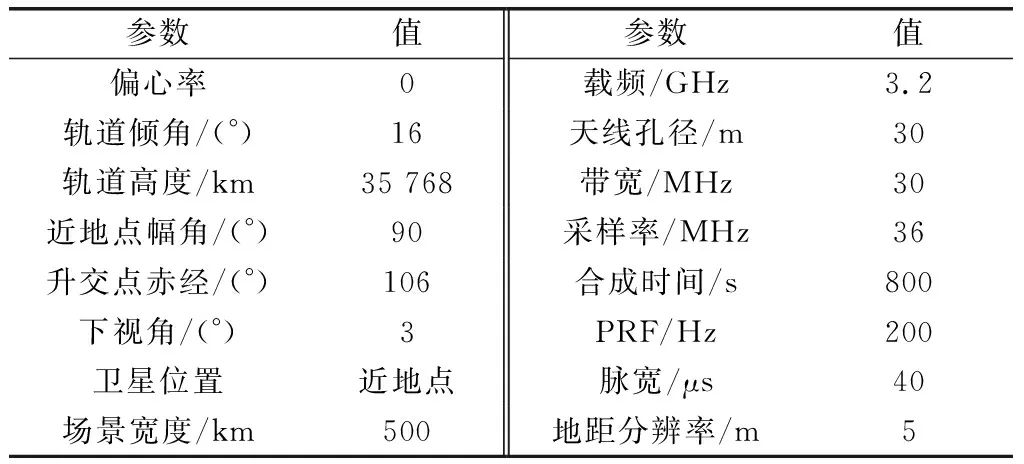
表1 GEO SAR系统参数

2.1 距离空变SVD特性分析

根据式(5),距离信号经过SVD后可以表示为

(6)

式中,Url(fr;fa)·Vrl(RB;fa)是距离SVD的第l个特征分量;对每个多普勒单元fa,Url(·)是距离频率fr的多项式函数,Vrl(·)是距离RB的多项式函数。

距离空变会随着距离分辨率和距离场景宽度的增加而加剧。在一定的距离分辨率下,当距离场景宽度不是非常大时,用距离SVD的第一个特征分量表示距离信号的剩余相位误差Φr_error_1(RB)<π/4 rad,第一个特征分量可以精确地表示距离信号;随着距离场景的增大,距离信号将需要两个或更多的特征分量才能精确表示。图2给出了在表1的系统参数下,不同距离场景宽度对应的剩余相位误差Φr_error_1(RB),其中蓝色实线表示剩余相位误差,红色虚线表示π/4 rad的精度要求。从图2中可以看出,当距离场景宽度为150 km时,距离信号可以用第一个特征分量精确表示;而当场景宽度非常大时,例如500 km时,距离信号必须用两个甚至更多的特征分量才能精确表示。

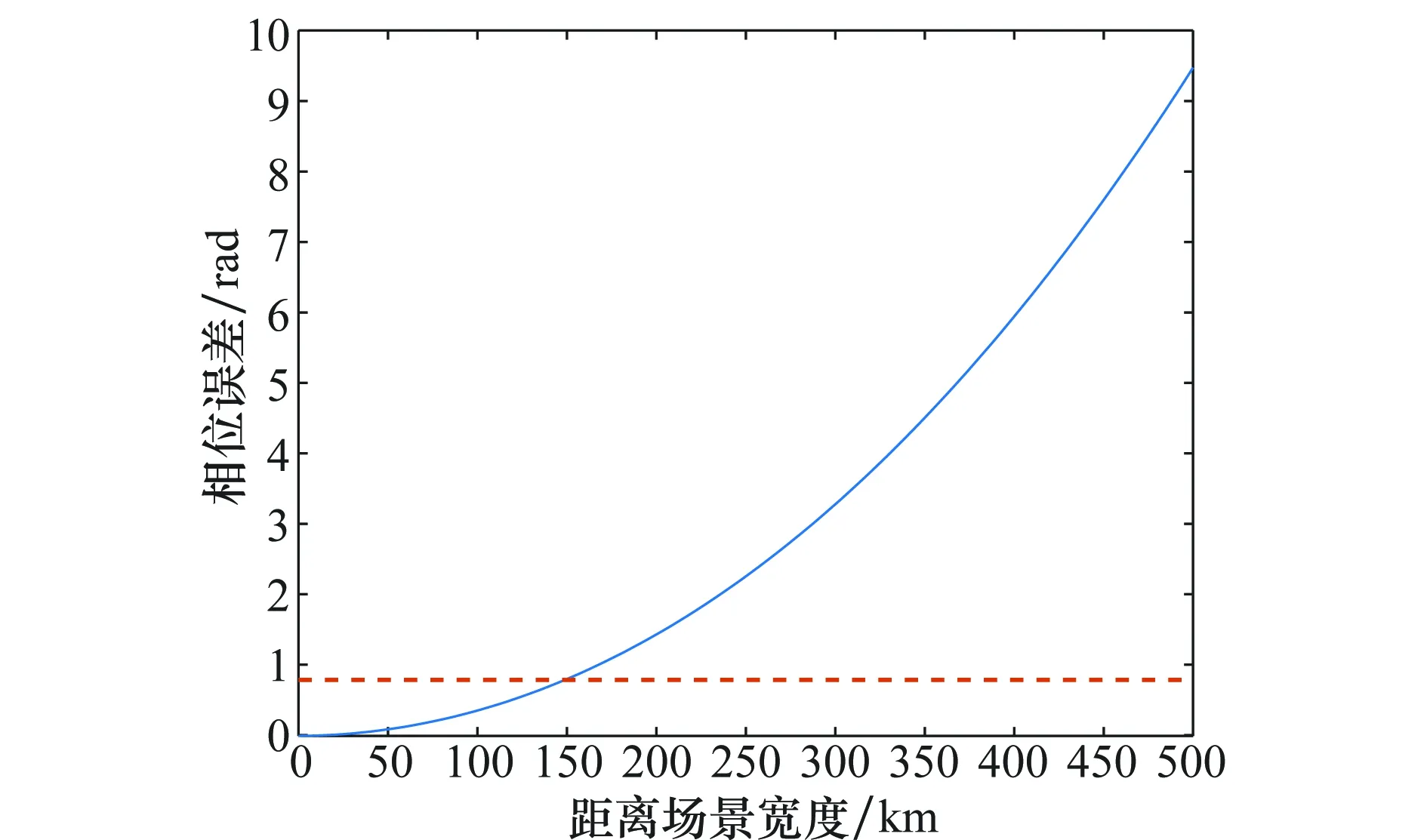
图2 距离空变SVD特性分析Fig.2 Range variation analysis by SVD

2.2 方位空变SVD特性分析

与距离空变SVD特性分析类似,可以得到方位信号的SVD结果

(7)

式中,Ual(fa;RB)·Val(X;RB)是方位SVD的第l个特征分量;对每个距离单元RB,Ual(·)是多普勒频率fa的多项式函数,Val(·)是方位位置X的多项式函数。

与距离信号类似,方位空变也随着方位分辨率和方位场景宽度的增加而加剧。在一定的方位分辨率下,仿真分析了不同方位场景宽度下的SVD结果如图3所示。

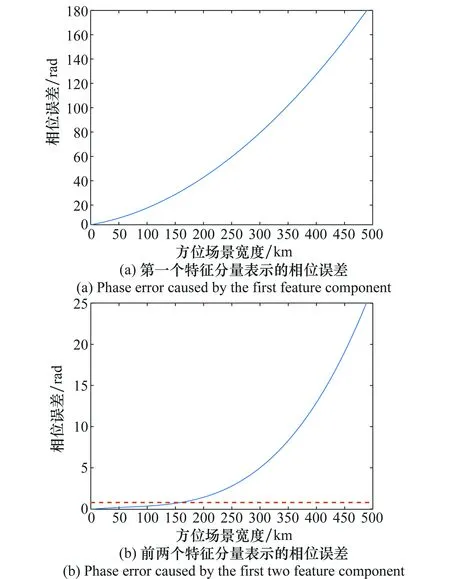
图3 方位空变SVD特性分析Fig.3 Azimuth variation analysis by SVD

由于方位信号的空变相较于距离信号的空变更严重,方位信号可能将不能用一个特征分量简单表示,因此图3(a)给出了用方位SVD的第一个特征分量表示方位信号的剩余相位误差Φa_error_1(X),图3(b)给出了用方位SVD的前两个特征分量表示方位信号的剩余相位误差Φa_error_2(X)。从图3(b)中可以看出,在方位场景宽度为150 km时,方位信号需要用两个特征分量精确表示,当方位场景继续增大时,方位信号甚至需要3个或者更多的特征分量才能表示。用第一个特征分量表示方位信号虽然可以通过简单的插值处理校正方位空变,但是从图3(a)可以看到,一个特征分量基本无法精确表示方位空变信号,而且方位分块操作存在很多问题,例如在经过方位分块处理后会出现栅瓣现象,使成像质量降低。针对两个特征值能够表示方位信号的情况,文献[24]提出了一种级联的方位SVD方法校正方位空变,可以对较大的方位场景完成方位空变校正,得到很好的聚焦效果。本文在经过距离空变校正后将采用该方法完成方位空变校正及方位聚焦。

3 基于SVD的GEO SAR成像方法

图4给出了本文提出的GEO SAR两维奇异值分解成像方法流程图,其处理步骤主要可以划分为两个部分:第一部分是基于距离块的SVD-RCMC算法,通过一次距离SVD实现距离空变校正;另一部分是级联的方位SVD-NCS算法,通过级联的两次方位SVD完成方位空变校正。

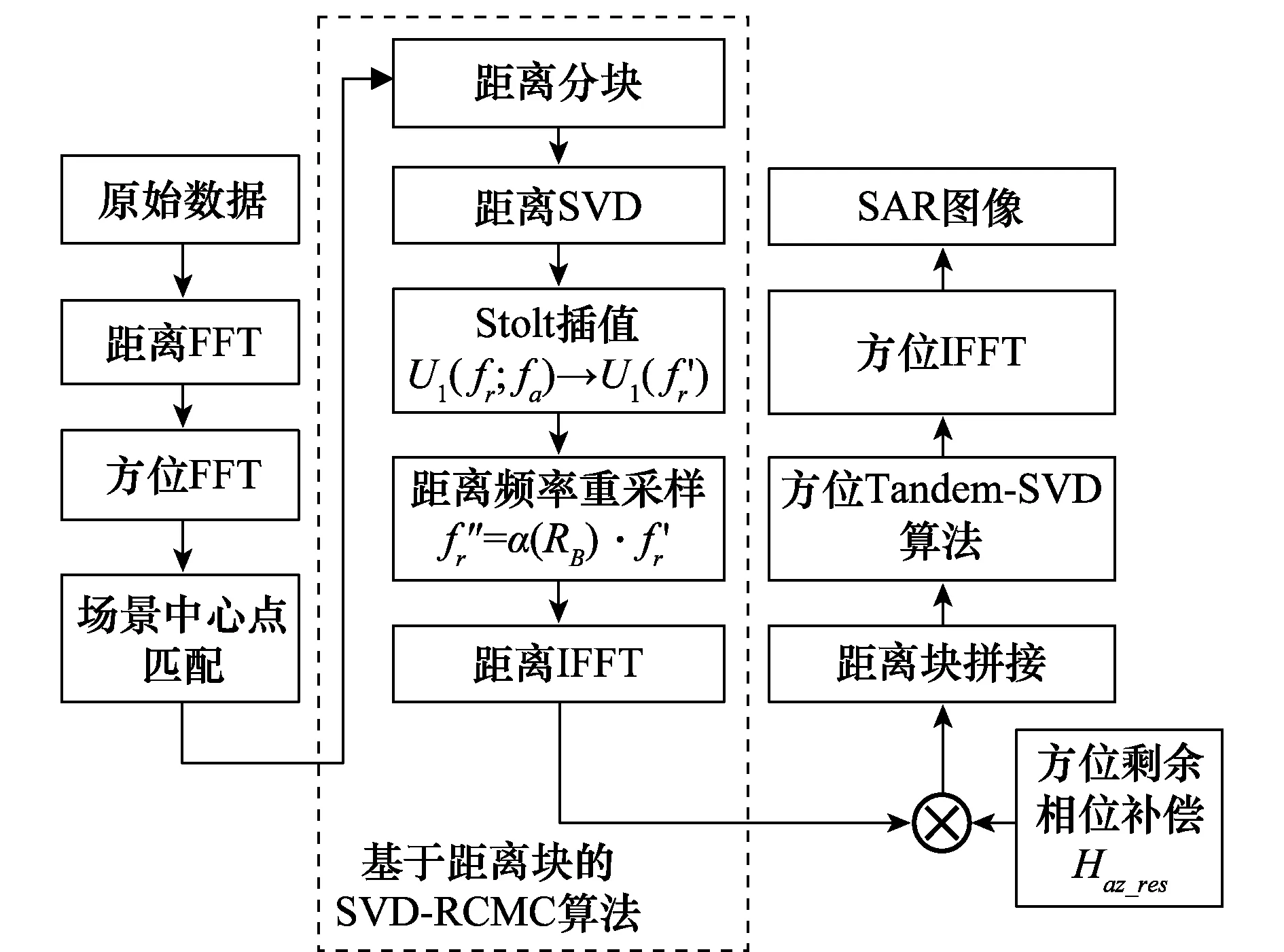
图4 算法流程图Fig.4 Block diagram of algorithm

3.1 基于SVD的距离空变校正方法

由第2.1节的距离空变的SVD分析结果可知,在较大的子距离块中与距离空变的RCM校正相关的距离信号可以用SVD后的第一个特征分量表示

Φr(fr,RB;fa)=Ur1(fr;fa)·Vr1(RB;fa)

(8)

在GEO SAR曲线运动轨迹情况下,通过SVD得到的特征向量Ur1(fr;fa)和Vr1(RB;fa)分别是fr和RB的高阶多项式。注意到各特征向量为数值列向量,因此可以通过数值方法得到多项式的各阶系数[30],通过仿真分析可知高阶项(三阶及以上)对相位的影响远小于π/4 rad,可以忽略。故下面将Ur1(fr;fa)和Vr1(RB;fa)分别对fr和RB展开到二阶:

(9)

注意到式(8)和式(9)中的参变量fa,它代表着距离与多普勒的耦合。对每一个多普勒单元均进行式(8)的距离SVD,可以得到距离与随多普勒变化的系数Ai(fa)、Bi(fa)之间的耦合关系。利用距离SVD得到的这个耦合关系,将每个多普勒单元的距离信号通过插值和重采样变换到参考多普勒单元的参考距离信号即可实现距离空变的RCM校正。

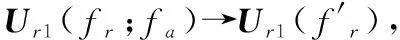
(10)

式中,系数C0和C1将通过下面的参考多普勒处的SVD得到。考虑到选取的参考多普勒单元将带来的形变问题,选取多普勒中心fdc作为参考多普勒单元,参考多普勒处的SVD结果由下式给出

Φr(fr,RB;fdc)=Ur1(fr;fdc)·Vr1(RB;fdc)=

(11)

经过式(10)的第一次Stolt插值后,距离信号表示为

(12)

观察式(11)和式(12),可以发现通过构造下面的距离空变的距离频率重采样方程即可完成距离空变的RCM校正

(13)

其中重采样系数α(RB)为

(14)

经过距离空变校正后,距离信号表示为

(15)

式中,等号右边第一项与多普勒有关的相位是距离SVD处理引入的方位剩余相位,会影响之后的方位聚焦处理导致散焦。通过在距离多普勒域构造相应的补偿函数将其补偿为与参考多普勒单元(即式(11))相同的形式,即可完成方位剩余相位补偿。方位剩余相位补偿函数为

Haz_res(RB,fa)=exp(-jC0(B0(fa)+

(16)

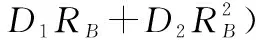
exp(jΦa(fa,X;RB))

(17)

注意到,因为本节的距离空变的RCM校正处理仅对距离频率fr进行操作,不会对方位聚焦相位Φa(fa,X;RB)产生影响,故下面可以直接对方位信号Φa(fa,X;RB)进行级联的SVD完成方位聚焦。

3.2 基于SVD的方位空变校正方法

经过第3.1节的距离空变的RCM校正后,在每个子距离块中,与距离信号类似,式(17)中的方位信号是二维空变的。文献[24]提出了一种级联的SVD-NCS方位空变校正方法,在这里可以通过该方法校正方位空变完成方位聚焦。下面对该方法进行简单的描述。

对子距离块中的每个距离单元RB的方位信号进行SVD,根据第2.2节的方位空变SVD特性分析结果,分解后的信号需要由两个特征分量表示。级联的SVD-NCS方法首先通过第一次SVD-Stolt补偿第一个特征分量(即主要特征分量)的高次项,然后通过在方位时域引入一个三次扰动函数,使得与三次扰动函数相乘后的信号的二维频谱经过第二次SVD分解可以仅由一个特征分量表示,最后对整合后的这个特征分量进行Stolt插值即可完成方位空变校正。

4 仿真结果及分析

4.1 距离空变校正结果

仿真场景点目标分布如图5所示,其中距离向场景宽度为300 km,方位向场景宽度为100 km。仿真系统参数如表1所示。为了验证本文提出的基于SVD的距离空变校正方法的有效性,下面首先给出大距离测绘带的距离空变校正结果。

采用本文算法对大距离测绘带进行距离空变的RCM校正,图6(a)给出了距离中心点匹配后的A点信号包络,可以看到距离空变严重,将影响距离聚焦;图6(b)为距离中心点匹配后的中心点O的信号包络。本文所提方法的目标是通过一次SVD将各距离单元点目标包络校直。图7(a)给出了直接对A点进行一次距离SVD空变校正后的包络结果,可以看到包络未被完全校直,距离空变未被完全校正,将影响距离聚焦结果;根据第2.1节的距离空变SVD特性分析结果,图7(b)给出了经过150 km距离分块后的距离空变RCM校正结果,可以看到经过距离分块后,场景边沿点目标的包络被校直,距离空变被校正。

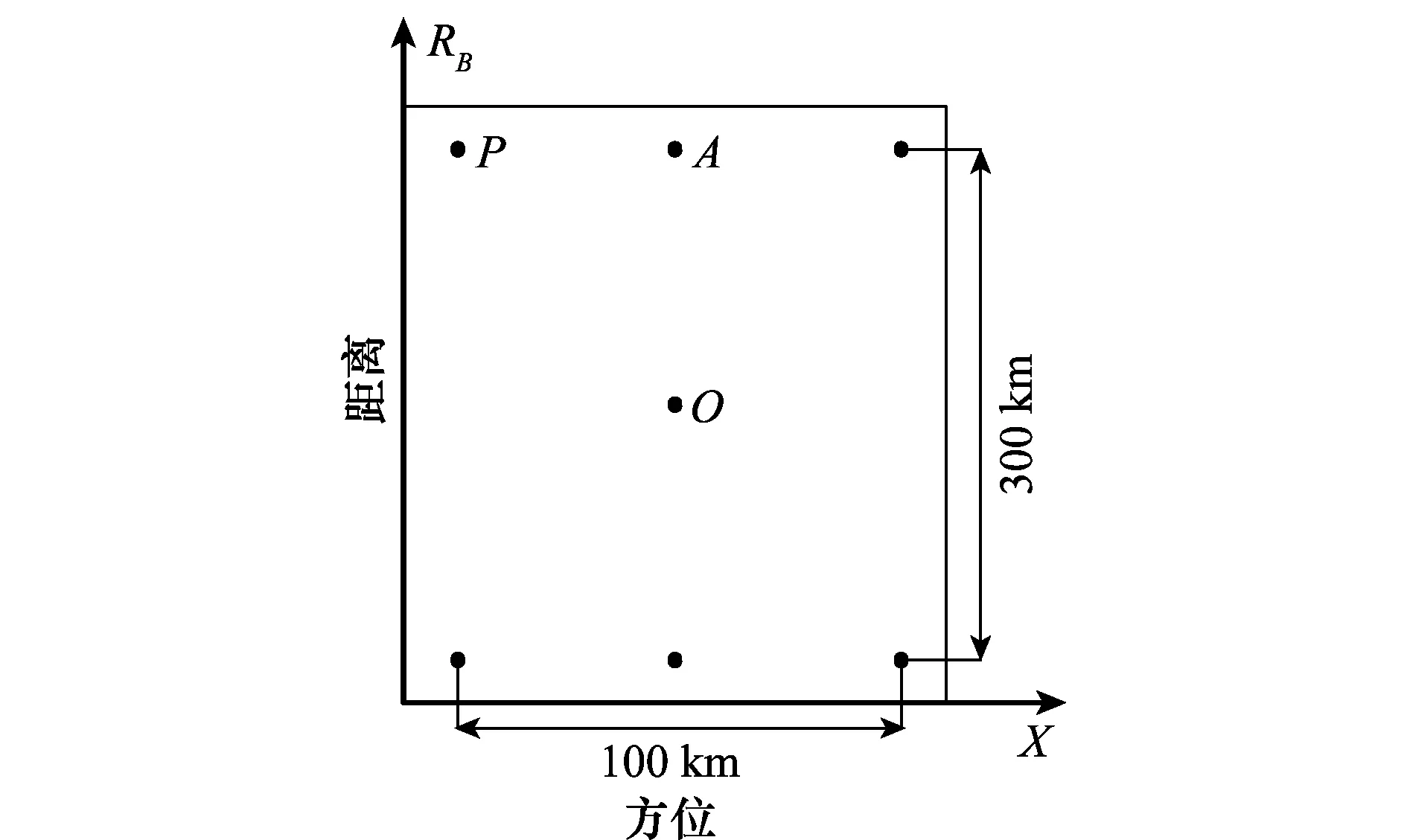
图5 仿真场景示意图Fig.5 Simulation scene

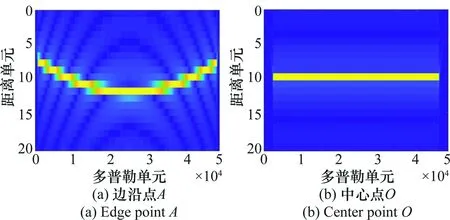
图6 中心点匹配后点目标包络Fig.6 Signal envelope after center point matching

图7 距离空变校正结果Fig.7 Range variation correction result

4.2 点目标成像仿真

采用本文提出的两维SVD成像方法对图5中设置的300 km×100 km的场景成像。图8和图9分别给出了文献[18]和本文方法对场景边沿点目标P成像的等高线图,方位剖面图和距离剖面图。从图8中可以看到,由于还存在空变的三次项,点目标副瓣抬升,散焦严重。而从图9中可以看到,采用本文提出的两维SVD成像方法,点目标距离和方位均聚焦良好,其距离PSLR和ISLR分别为-13.26 dB和-10.15 dB,方位PSLR和ISLR分别为-13.20 dB和-10.23 dB,均非常接近理论值,满足成像需求,验证了本文方法的有效性。

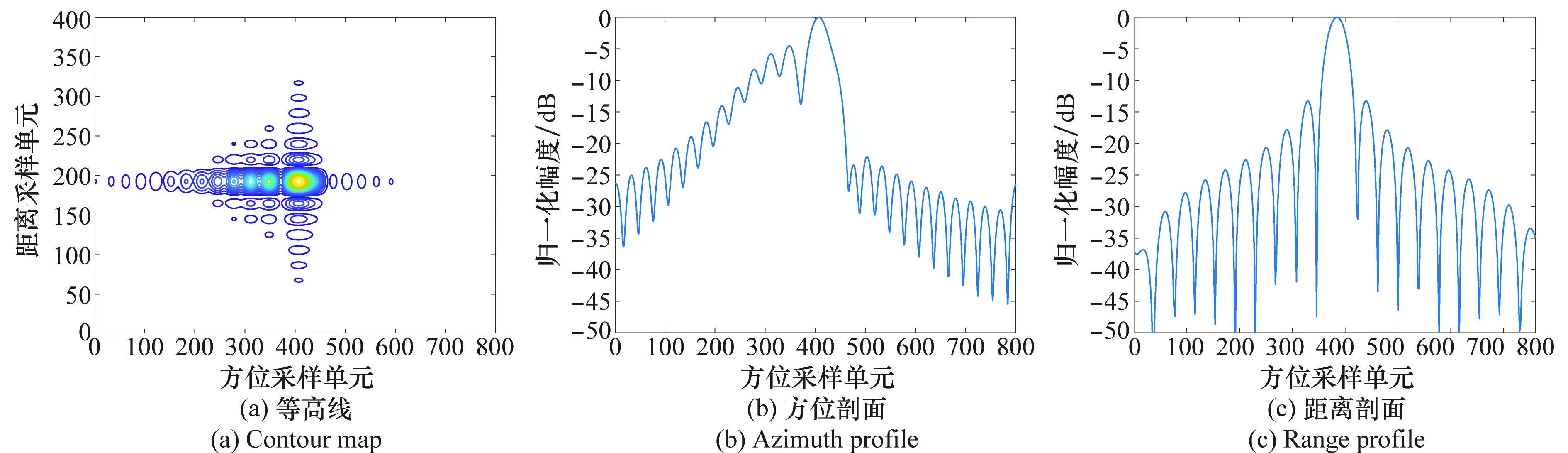
图8 文献[18]对场景边沿点目标P成像结果Fig.8 Imaging result of point P by reference[18]

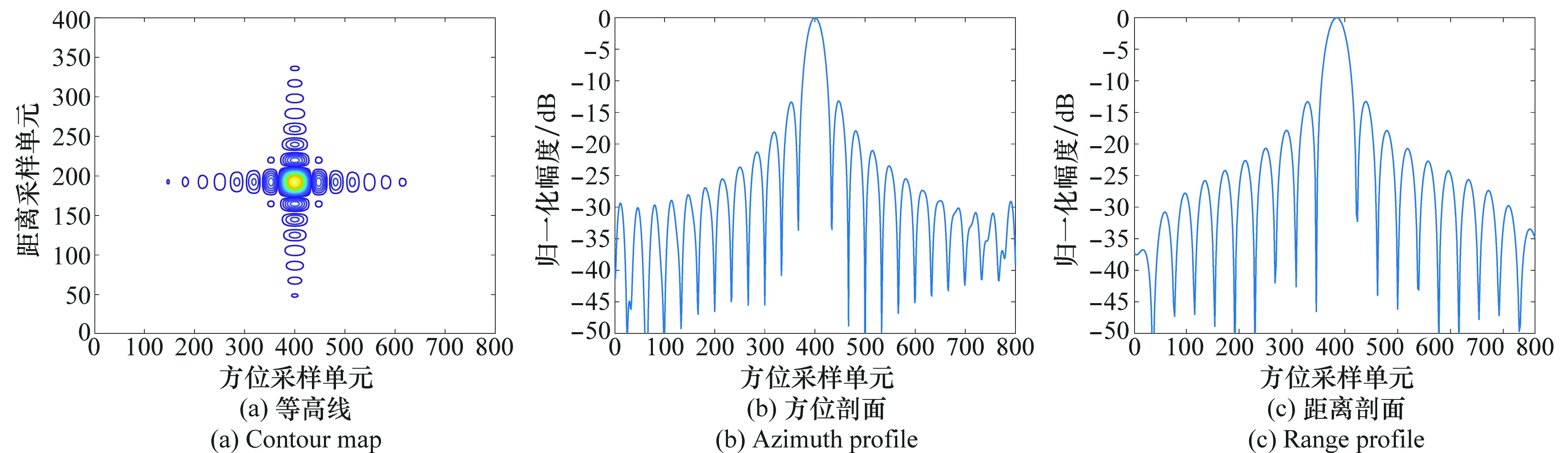
图9 本文所提算法对场景边沿点目标P成像结果Fig.9 Imaging result of point P by this paper

5 结 论

本文以地球同步轨道SAR为背景,研究了长合成时间宽测绘带情况下严重的二维空变问题。本文提出了一种基于奇异值分解的地球同步轨道SAR两维成像方法,该方法不需要对二维空变的二维频谱进行复杂的推导构造处理函数,而是通过奇异值分解对空变的信号进行分析,然后利用空变信号奇异值分解后的特性先通过距离Stolt插值和距离频率重采样的方法校正距离空变,最后采用一种级联的SVD-NCS算法校正方位空变。仿真结果验证了本方法的有效性。