半变系数模型的几乎无偏岭估计探讨

2018-10-09曹连英徐文科

统计与决策 2018年17期

曹连英，王蕾，张博，徐文科

（东北林业大学理学院，哈尔滨 150040）

0 引言

考虑如下的半变系数模型：

其中，y是响应变量，(xT，zT，u)是相应的协变量，xT=(x1，x2，…，xp)，zT=(z1，z2，…，zq)，u为时间变量或空间变量，为研究方便，本文假定u为一维变量；β=(β1，β2，…，βp)T为未知常值参数，α(·)=(α1(·)，α2(·)，…，αq(·))T为未知函数。ε为随机误差，满足E(ε|xT，zT，u)=0和Var(ε|xT，zT，u)=σ2。

半变系数模型，因其含有部分线性模型，使之与非参数回归模型比较具有更好地外延性；又因其变系数部分能充分体现协变量对响应变量在时间或空间上影响的差异性，使之与线性回归模型相比有更强的灵活性。使半变系数模型受到相关学者的广泛关注，已经提出了大量有价值的估计方法[1-5]，如：小波估计法[1]、局部多项式拟合方法[2]、一般级数方法[4]、轮廓最小二乘估计法[5]等。然而已有研究中直接或间接假设协变量xT=(x1，x2，…，xp)的系数矩阵列满秩，即不具有复共线性。而实际问题中会遇到多重共线性问题，即xT的系数矩阵是病态矩阵，或者是非列满秩的，这时利用一般的方法所得到估计结果的某些分量方差很大，使得估计值的精确度变差，甚至可能导致某些变量系数的估值正负符号与实际问题意义不符。对于病态或秩亏的线性回归模型已经开展了深入研究[6，7]，其中岭估计方法是有效解决这一问题并且使用广泛的一种有偏估计方法。近几年来，岭估计方法被逐步应用到非线性回归模型中。本文基于轮廓最小二乘方法给出半变系数模型的岭估计和几乎无偏岭估计。

1 半变系数模型的岭估计和几乎无偏岭估计

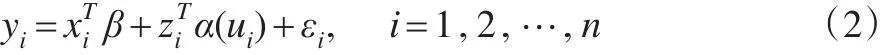
假定模型（2）中p维待估参数β已知，记，则模型（2）可写成如下的变系数模型：

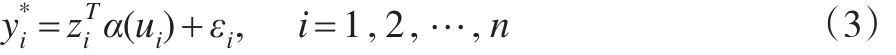
利用局部多项式拟合方法来估计变系数未知函数{αj(·)，j=1，2，…，q}。对给定u0附近的一点u，对αj(u)利用Taylor展开有：

应用局部加权最小二乘极小化：

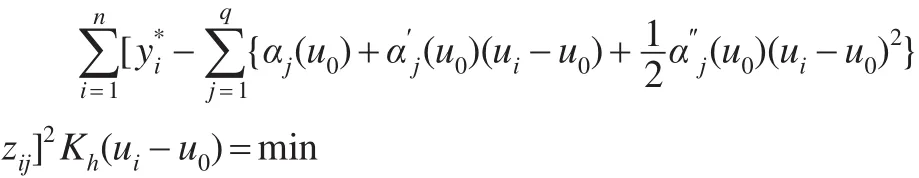
其中Kh(·)为给定的核函数，Kh(·)=K(·/h)/h，h为带宽。即可得到的估计。

为便于叙述，本文引入一些记号：

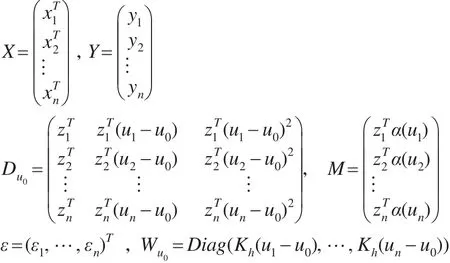
则模型(3)的矩阵形式为：

利用轮廓最小二乘估计方法可得α1(u0)，…，αq(u0)，的估计为：

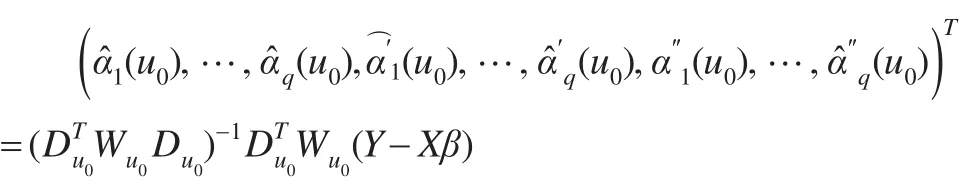
取u=u，得未知系数函数α(u)=(α(u)，…，α(u))T的

0i10q0估计：

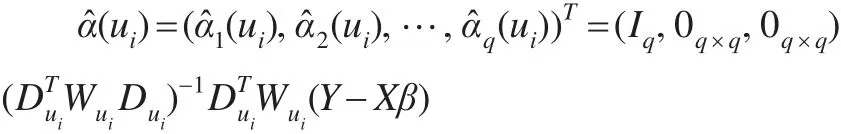
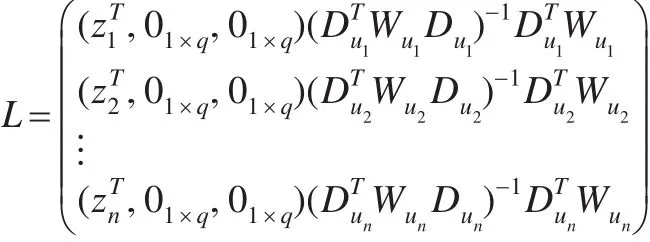
若模型(1)中协变量xT存在复共线性问题，会导致模型(5)中的接近奇异，从而β的轮廓最小二乘估计不能很好地解释实际问题。为此本文引入半变系数模型的岭估计方法[8]，并将岭估计方法进行改进。

为研究方便，令Φ=(Φ1，Φ2，…，Φp)为正交矩阵，满足即有偏强的复共线性性。记，模型（5）为：

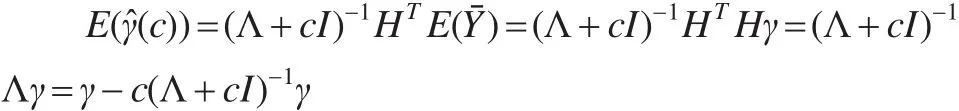
将模型(6)的岭估计修正为：

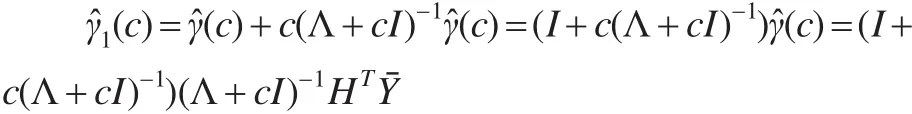
则模型(5)的参数部分系数的几乎无偏岭估计为：

变系数函数在ui处的估计α(ui)为：

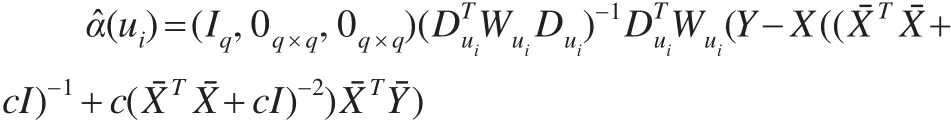
2 几乎无偏岭估计的性质

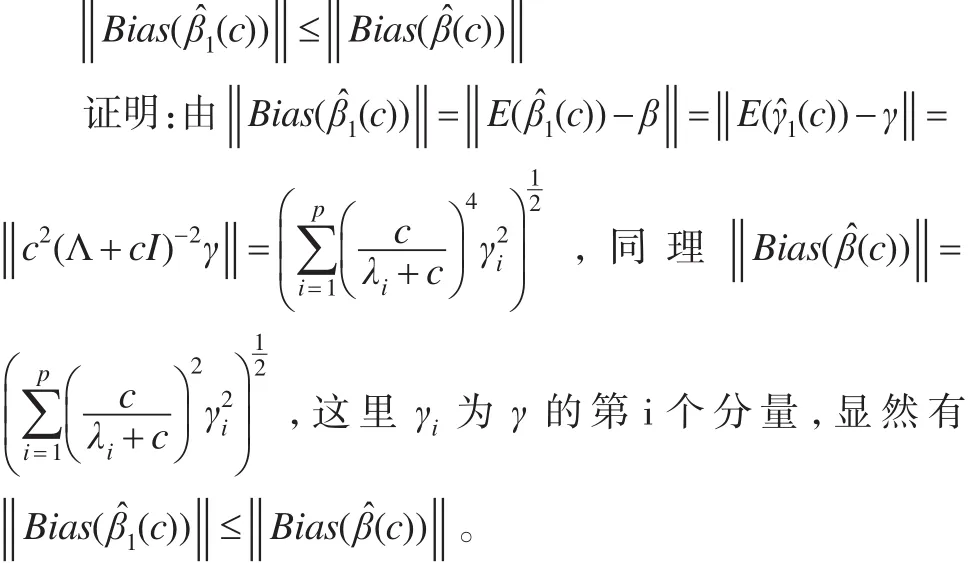
定理2：存在c*＞0，使得下面的式子成立：

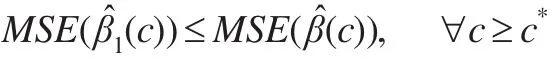
此估计方法中涉及的两个参数：光滑参数h和岭参数c。参数h的选取可采用交叉确认等方法确定，岭参数c的选取应使下式达到最小，即：

3 模拟实验

模拟如下半变系数模型：

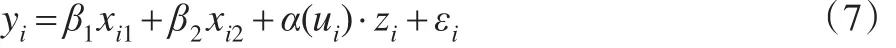
假定样本数为n，协变量x1的观测值x11，x21，…，xn1为从均匀分布U(-1，1)中独立抽取的n个随机数，变量x2与x1具有偏强复共线性性，条件数，不妨令xi2=2xi1+d，i=1，2，…，n(d的大小可以影响条件数k，一般地，d越小k越大)，协变量z的观测值z1，z2，…，zn为从区间(-1，1)上的均匀分布U(-1，1)中独立抽取的n个随机数；u为区间[-1，1]上的n个等分点；ε1，ε2，…，εn为从正态分布N(0，σ2)中独立抽取的n个随机数。yi由公式（7）得到。对n组样本数据 (yi，xi1，xi2，zi，ui)，i=1，2，…，n基于本文方法利用matlab编程，重复抽样N=50次比较岭估计和几乎无偏岭估计的优劣。

半变系数模型的实验结果(两种模型参数实验，每种模型参数记录3组实验结果)如表1所示，变系数函数的拟合曲线见图1，以及岭参数c与均残差平方和SSE的关系见下页图2。

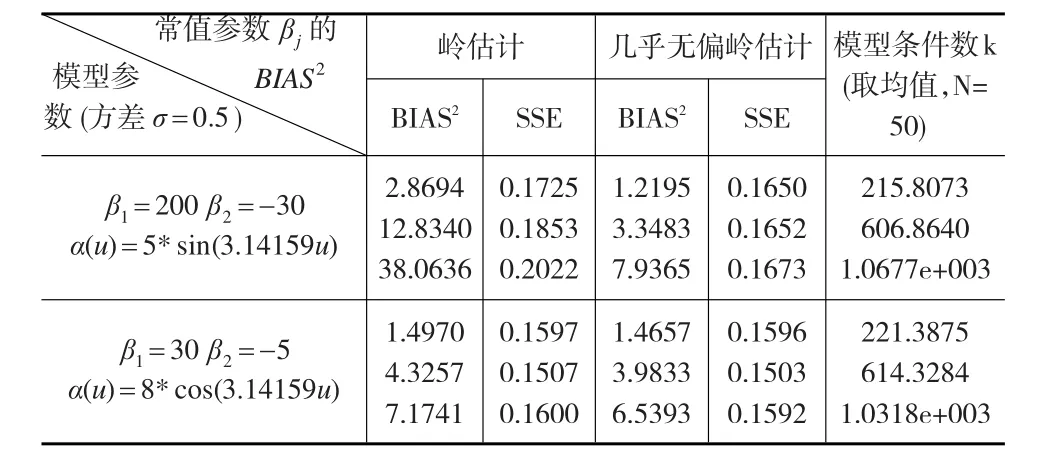
表1 不同估计的均偏差方(BIAS2)与均残差平方和(SSE)的比较

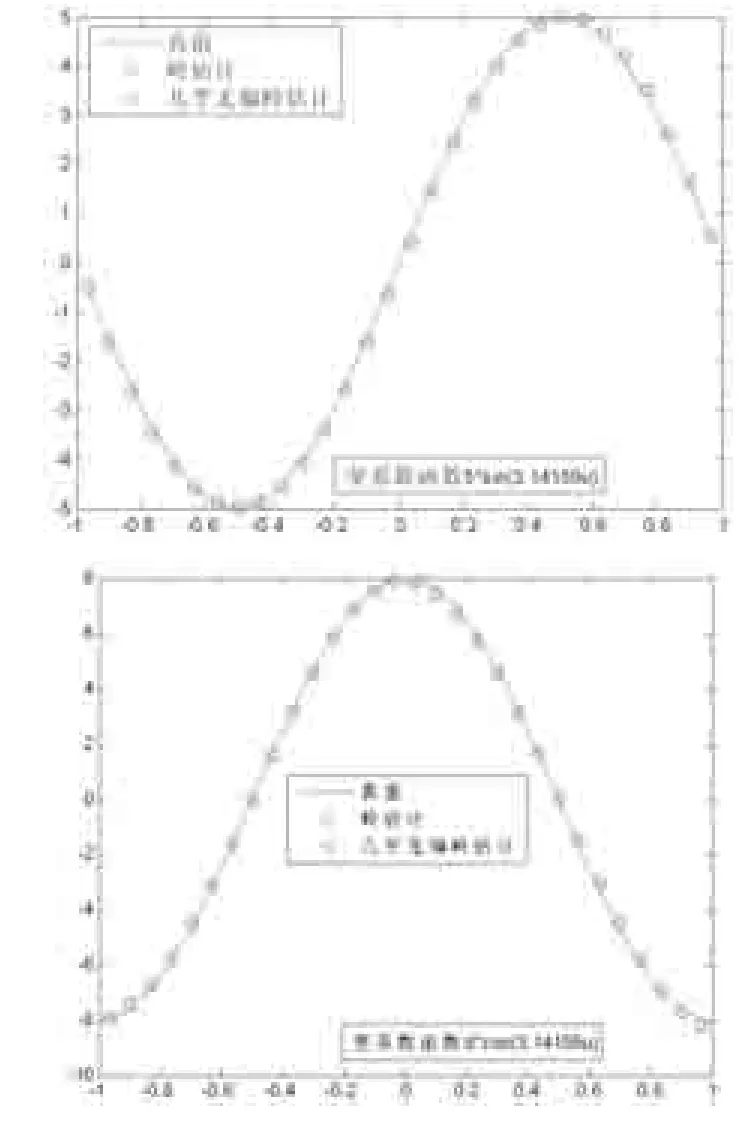
图1模型中变系数函数在方差为0.5下的拟合图

数值结果表明，在同一个模型参数下，几乎无偏岭估计的常值参数βj的BIAS2与模型的SSE均小于岭估计的BIAS2与模型的SSE。图1也表明了几乎无偏岭估计的变系数函数的估值最接近于真值，拟合程度更好。图2表明光滑参数相同时条件数不同下，模型的几乎无偏岭估计残差总是明显小于岭估计的残差，且随着岭参数的增大而几乎无偏岭估计的残差趋于稳定。