不完全多重共线性定义存在的问题及其修正建议

王义闹，张向文

(温州大学数理与电子信息工程学院，浙江温州 325035)

1 基本假定

考虑多元线性回归问题：Y为被解释变量，为解释变量，u是与解释变量无关的、方差为σ2的0均值随机干扰项.它们之间有如下关系：

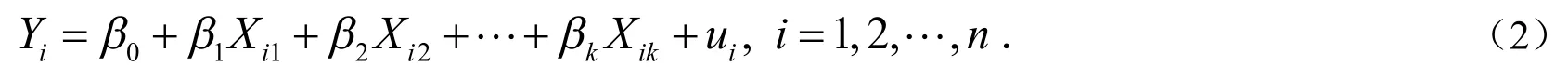
假设ui是来自u的简单随机样本，且与线性无关（或记

则（2）式可表示成：

其中X称为回归设计矩阵或资料矩阵.

2 不完全多重共线性定义存在的问题

文[1]指出了目前广泛应用的计量经济学教材[2-8]中不完全多重共线性定义存在的问题，但仅就解释变量为随机变量的情况给了一个新的定义.本文试图进一步分析不完全多重共线性概念的内涵与外延，给出合理定义.

下面分析广泛使用的计量经济学教材和应用回归分析教材中给出的三种定义存在的问题.

2.1 计量经济学教材中存在的问题1

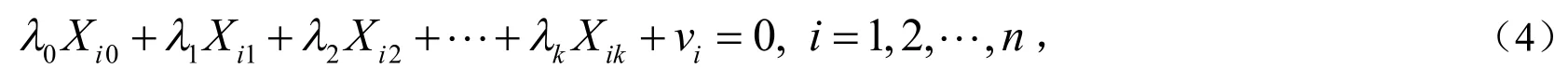
其中vi为随机变量（X0表示所有样本都取1的解释变量）.

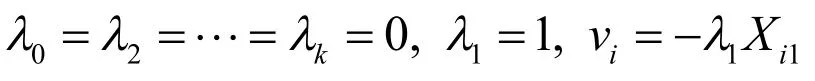
使（4）式成立.

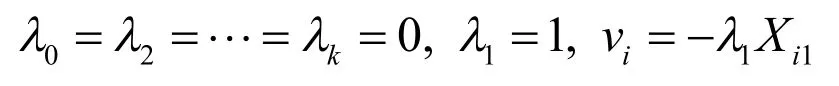
使（4）式成立.

所以，如上定义不完全多重共线性显然是有问题的.

2.2 计量经济学教材中存在的问题2

文[3]中给出：对模型（1），如果存在

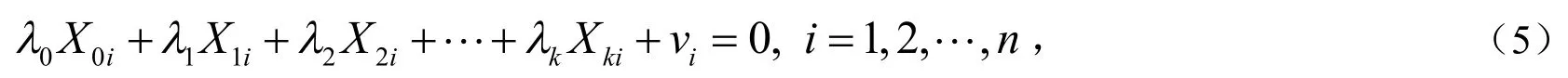
注：这里对原文定义增加了λ0Xi0，否则只适用于讨论中心化数据.

目前广泛应用的计量经济学教材[4-9]中都是这样定义的，这样定义也有问题.

首先，按文[3]P31中给出的随机干扰项定义

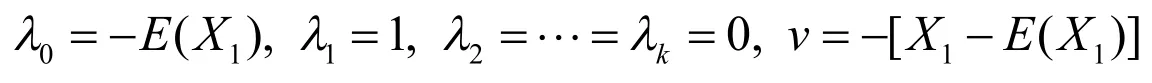
所以上述定义也不能表达近似共线性的涵义.

2.3 应用回归分析教材中存在的问题

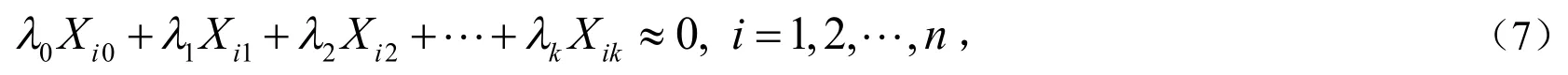
这一定义中约等于0是不确定的，无法验证的.

2.4 随机解释变量之间存在多重共线性还是样本之间存在多重共线性

文[2-3]中给出了检验一个解释变量与其他解释变量之间是否存在多重共线性的F检验方法，实际上，检验的是具有特定分布的一个解释变量与其他具有特定分布的随机解释变量之间是否存在显著复相关性；而文[3]P115又特别指出，“多重共线性是一种样本现象.同一个模型在一个样本下可能表现出多重共线性，而在另一个样本下可能就不存在多重共线性”.文[9]P104也特别指出，“从本质上讲，多重共线性是样本现象，所以相同模型，不同样本条件下，可能出现共线性严重程度完全不同的情况.”究竟是变量间存在多重共线性，还是样本存在多重共线性？

还有一个问题是：已经有了随机变量之间的复相关概念，还有必要讨论变量之间是否存在多重共线性吗？

3 不完全多重共线性的定义

我们认为，合理的定义应该满足以下基本原则.

第一，定义的基础必须明确.定义的基础是解释变量还是样本必须明确，是满足某性质的解释变量还是满足某性质的解释变量的观测值，是首先要明确的.

第二，定义的内涵必须明确.（7）式中的约等于0是不明确的，我们不清楚多小才是约等于0.

第三，定义的外延必须明确，是一个康托集.如果定义的外延是模糊集，就不是普通概念而是模糊概念了.（4）式（5）式要求至少有一个解释变量是随机变量，而（7）式解释变量是确定性变量，两者外延不同.

第四，定义要概括人们具体对象的认识.

第五，符合定义的对象，应该有公认的性质——与没有共线性的情况相比，参数估计量具有较大方差.

第六，好的定义要给后继内容的简洁阐述打好基础.

下面进行具体分析.

第一，考虑光照时间X1，浇水量X2，施肥量X3对小麦亩产Y的影响，我们可以设计实验，使向量

正交，也可以使这三个向量线性相关，这与解释变量之间是相关还是独立没有关系.

因此，不完全多重共线性应该以样本为基础定义.在多元线性回归问题中，解释变量可以是确定性变量，见文[11-13]；也可以是随机变量，见[2-8].以样本为基础进行定义，就可以既适用于随机解释变量，又适用于确定性解释变量.

第二，满足什么性质的样本具有不完全多重共线性必须明确.不能说相关性强就有多重共线性，因为“强”不是明确的性质；“约等于0”也不是明确的性质.一个样本，“有没有”、“存在不存在”多重共线性必须明确，二者必居其一，不能模棱两可.在定义了存在不存在多重共线性之后，再定义多重共线性的强弱.

基于以上两点我们给出如下的定义.

定义1 当存在一个解释变量（不妨设为X1）与其他解释变量的样本复相关系数大于0小于1时，就称设计矩阵X的第2列与其他各列之间存在（不完全）多重共线性.

如果存在设计矩阵X的某一列与其他各列之间存在（不完全）多重共线性，就称设计矩阵存在（不完全）多重共线性.

定义2 如果解释变量X1与其他解释变量的样本复相关系数为R1·，X2与其他解释变量的样本复相关系数为则称设计矩阵X的第3列与其他各列之间（比X的第2列与其他各列之间）存在较强多重共线性.对解释变量的两个样本X,X*，X1与其他解释变量的样本复相关系数依次为则称X*的第2列与其他各列之间（比X的第2列与其他各列之间）存在较强多重共线性.

第三，如上定义不完全多重共线性显然符合第三个基本原则，设计矩阵X有没有多重共线性，设计矩阵X的哪一列与其他各列之间有较强的多重共线性，不同设计矩阵X之间哪个有较强的多重共线性都是明确的.

第四，以样本复相关系数大小作为多重共线性强弱的定义，体现了X的各列之间相关性强共线性就强的认识.

第五，文[10]给出了βi的OLS估计量的方差

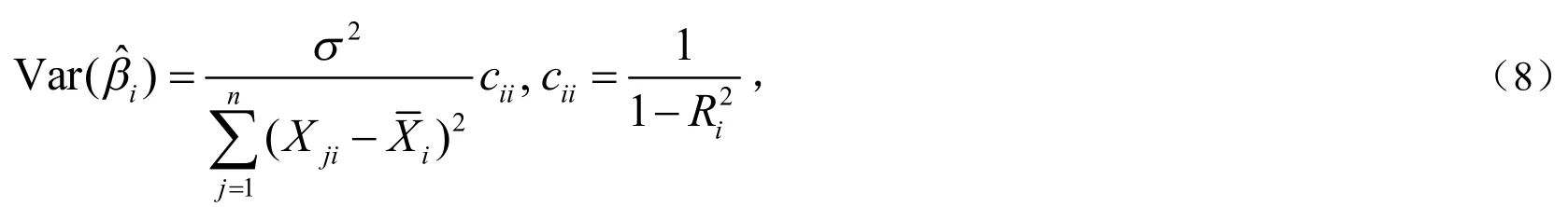
由（8）式可见，在Xi的离差平方和不变的条件下，Xi与其他解释变量的样本复相关系数Ri·等于0时，的方差最小；Xi的观察值列向量与设计矩阵X的其他各列之间的多重共线性越强，的方差越大.

由此可见，如上定义多重共线性的强弱，有利于解释多重共线性对参数估计量方差的影响.

综合上述讨论可见，应用复相关系数定义多重共线性是较好的方法.

文[10]指出，经验表明当VIFi≥10时，Xi的观察值列向量与设计矩阵X的其他各列之间有严重的多重共线性.这时的OLS估计的方差是不存在多重共线性条件下的OLS估计的方差的VIFi倍，偏离真值较远的概率显著增大.由于Xi与其他解释变量的样本复相关系数大于或等于Xi与任一解释变量的样本相关系数的绝对值，所以当Xi与任一解释变量的样本相关系数的平方小于0.1时，就有VIFi≥10，有严重的多重共线性.

现在通用的国内外教材讲解多重共线性，无非是为了发现多重共线性，进而改进参数估计.而这只与设计矩阵X有关，无需涉及解释变量，因此完全没有必要再引进解释变量共线性的概念.为解释样本呈现共线性的原因，可以说变量间存在复相关是样本呈现共线性的原因之一.

4 教材中讲解欠准确的两个知识点

第一个讲解欠准确的知识点是：“增加样本容量就有可能消除多重共线性”（见文[3]P115）.

事实上，如果Xi与其他解释变量的复相关系数为增加样本容量只是使样本复相关系数取值于附近的概率更大了，并不能使样本复相关系数减小，当然也就不可能消除多重共线性.我们赞同文[10]指出的，“当时，Xi的观察值列向量与设计矩阵X的其他各列之间就有严重的多重共线性”，而无论样本容量有多大.当然由（8）式可见，在VIFi不变的情况下，增加样本容量可使解释变量的离差平方和增大，的方差减小，提高参数估计精度，因此准确地讲解应该是“增加样本容量可以减小多重共线性对参数估计带来的不利影响”.

实际上，当Xj与其他解释变量的样本复相关系数等于0.1，其他解释变量有2个，只要样本容量为1 003，就有大于应在显著性水平0.05下拒绝原假设.这时，其他解释变量的线性组合只能解释Xj的变差的1%，还把检验结果理解为是其他解释变量的线性组合，显然是一种误解.理论上，这个F检验是检验Xj与其他解释变量是否有显著复相关，而不是检验解释变量的观察值是否存在不完全多重共线性，不完全多重共线性是否严重.Xj与其他解释变量显著复相关，不一定就高度复相关，其样本也就不一定存在严重不完全多重共线性.只有当Xj与其他解释变量高度复相关时，才可以把Xj近似看成是其他解释变量的线性组合.