自相关过程的EWMA残差控制图的设计与性能评价

尚云艳，郭鹏江,夏志明

（1.西京学院a.理学院；b.科研处；2.西北大学 数学学院，西安 710123）

0 引言

统计过程控制（SPC）已在制造业得到了广泛应用，相关研究已比较成熟，其目的是用来监控生产过程，检测异常波动，寻找并消除产生异常波动的原因。控制图是实施过程监控的有效工具，它的使用基于一个重要的假设，即过程受控时产生的数据是独立且服从正态分布的。但是实际数据通常表现出某种程度的自相关性[1]，如宏观经济、金融数据等均表现出不同程度的相关性。在违背独立性假设的情况下，如果在原始数据上直接应用传统控制图，则会使得控制图的误报率增加。为更有效地监控生产过程，众多学者提出残差控制图，即先拟合自相关过程的时间序列模型，再利用拟合模型的残差相互独立且服从正态分布的特性，以传统控制图直接监控残差序列值。

传统控制图对中小漂移检测的灵敏性参差不齐，因此，为提高中小漂移的检测效能，Roberts（1959）[2]提出了指数加权移动平均（EWMA）控制图，EWMA控制图的特点是利用了历史数据，且该控制图可以对不同阶段的数据取不同的权重，距今越近的数据权重越大，距今越远的数据权重越小，它主要检测统计过程控制中的微小波动。

Zhang（1997）[3]定义了检测能力指数，将其应用于广义平稳随机过程模型，通过蒙特卡洛模拟，与传统控制图相比较，在调整广义平稳随机过程模型的参数条件下，残差控制图对中小漂移的检测效能得到提升；张志雷（2012）[4]基于同样的思想将信噪比指标应用于自相关控制图，通过蒙特卡洛模拟，与传统控制图方法相比较，在调整ARMA模型参数的条件下，自相关控制图对中小漂移的检测效能同样得到提升。

目前还没有把过程检测能力指数思想与EWMA残差控制图方法相结合的研究，因此，本文在尚云艳等（2015）[5]的基础上将检测能力指数应用于基于二阶自相关过程(AR(2))的EWMA残差控制图，根据EWMA残差控制图检测能力的强弱，调整AR(2)模型的参数，运用蒙特卡罗模拟方法将其与传统残差控制图和自相关残差控制图进行比较分析其性能。

1 建立模型

由王振龙（2010）[6]可知 AR(2)模型：

其中，Xt(X0=0)是零均值化的序列变量值（t=1，2，…），φ1，φ2是模型参数，且满足约束：φ1+φ2＜1，

是随机误差项。一般地，通常对模型做以下假设：

假设2：自变量序列Xt只与Xt-1，Xt-2有关，与Xt-3，…，Xt-p(p＞2)无关，也与随机误差项εt不相关，即Cov(εt，Xt-k)=0 ，k=1，2，…。并且，如果E(Xt)=0 ，则过程受控；若E(Xt)=δσε（当δ≠0时），则过程失控。

2 构造EWMA统计量

2.1 基于AR(2)模型的残差

将参数估计值φ1、φ2代入模型（1）计算残差，即：

且依据自相关过程可知：

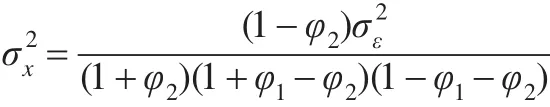
残差序列的自协方差函数为(k=1，2，...)：

根据尚云艳等（2015）[5]假设均值随时间变化，则自相关序列满足：

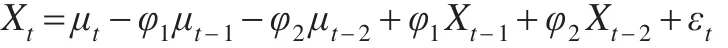
假设t=0和t=1时刻均值从0漂移δσx，则残差序列：

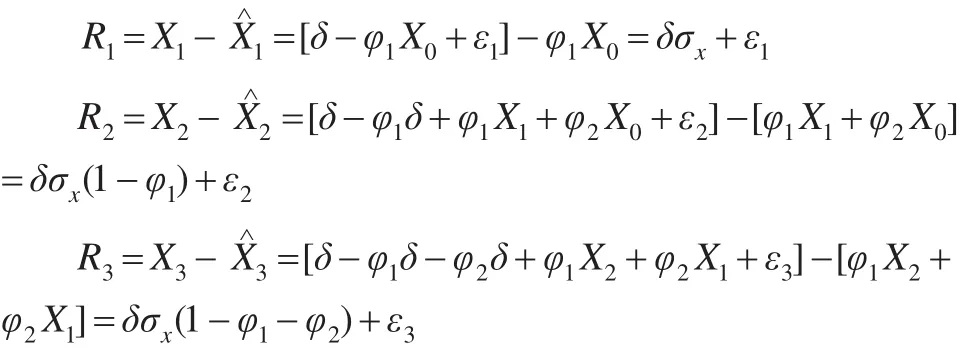
若假设过程均值不再发生变化，则残差序列可以统一用式（4）表示：

由上述分析可见，当过程均值发生漂移以后，第一个时刻残差的均值为δσx，但是自相关过程很快作出反应，第二个时刻残差的均值变为δσx(1-φ1)，第三个时刻残差的均值变为δσx(1-φ1-φ2)。当自相关参数φ1+φ2→1时，随后的残差与过程刚发生偏移时的残差相比会变得非常小，而难于检测出过程的偏移。由式（4）可知，当φ1+φ2为负或者为正且取值较小时，均值的变化对残差的影响增强了，即在该条件下，残差控制图的灵敏度将有所提高。

2.2 过程检测能力指数

Zhang（1997）[3]给出过程检测能力指数的定义：

f(t)是残差控制图在过程均值发生漂移δσε时（即t时刻）检测能力大小的一种度量，f(t)的值只取决于参数φ1、φ2、ρ1、ρ2的大小，与均值漂移δσε大小无关。当f(t)＞1时，残差控制图在t时刻的检测能力指数比传统控制图在t时刻的检测能力指数强，即表明残差控制图在t时刻的检测能力增强；反之，当f(t)＜1时，表明残差控制图在t时刻的检测能力减弱。

对AR(2)过程，当φ1+φ2或者φ2-φ1→1，1-φ1ρ1-φ2ρ2→0时，f(t)→∞，即AR(2)过程不平稳时，f(t)的值将会变得比较大，表明该时刻检测漂移的能力比较强；对AR(1)过程，当 |φ1|→1，φ2=0时，f(t)→∞ ，即AR(1)模型平稳时，t时刻的过程检测能力很强。

特别地，当φ1=φ2=0时，有f(t)=1，表明{Xt}是一独立的变量序列（反之亦成立），此时残差控制图和传统均值控制图的检测能力相同。

根据Zhang（1997）[3]定理1：对于平稳过程AR(2)：

2.3 EWMA残差统计量

对式（3）采用指数加权移动平均法得到统计量Zt，t=0，1，2，…，即：

若模型（1）开始时受控，则统计量Z0的期望为0，E(Z0)=δσx(δ=0)；若模型（1）开始时失控，则统计量Z1的期望和方差分别是E(Z1)=δ(1-φ1)σx(δ≠0)，E(Z2)=δ(1-根据式（5）可得，当t＞1，...时，该过程的检测能力指数f(t)=

综上所述,基于AR(2)模型的EWMA残差控制图控制线为：

其中,k为控制线系数。

3 控制图性能比较与分析

一般地，对于控制图的比较，都是在相同条件下比较，即在受控平均运行长度相同的情况下，比较失控平均运行长度。如果平均运行长度越短，说明控制图性能越好，越长则越说明该控制图的性能越不好。

运用Matlab软件给出一个满足模型（1）的AR(2)平稳过程，通过给定不同参数值，作10000次模拟运算，获得在不同漂移大小下各控制图的ARL值，具体结果见表1。

表1 不同参数φ1，φ2、δ下的控制图的ARL对比

当过程参数不同时，为便于比较，记φ1=1.5，φ2=-0.7为过程I，φ1=1.5，φ2=-0.95为过程II，根据式（2）过程I和过程II的一、二阶自相关系数结果均大于0，过程I的参数满足φ1+φ2-φ22＞0，有f(t)=0.5951＜1；过程II的参数满足φ1+φ2-φ22＜0，有f(t)=2.5554＞1，即过程均值发生漂移时，过程I的检测能力比过程II弱。从表1也可以看出，在过程均值发生0.5σε漂移时，过程I的自相关残差控制图和EWMA残差控制图的失控ARL分别是258.5369和224.7687，均大于过程II的34.5419和22.6026。同样的，记φ1=-0.1,φ2=0.4为过程III，φ1=-0.5，φ2=0.4 为过程IV，过程III和过程IV的一阶自相关系数均小于0，但是当过程均值发生漂移时，过程IV的失控ARL均小于过程III的失控ARL。可见当参数满足φ1+φ2-φ22＜0，传统残差控制图、自相关残差控制图和EWMA残差控制图的灵敏度均有所提高。

当过程参数相同时，且参数满足φ1+φ2-φ22＜0，自相关残差控制图与传统残差控制图相比较：自相关残差控制图检测性能好，比如当φ1=1.5，φ2=-0.95,δ=0.5时，自相关残差控制图的平均运行长度ARL=34.5419是传统残差控制图ARL=157.8806五分之一；EWMA残差控制图与传统残差控制图相比较：EWMA残差控制图检测性能好，比如当φ1=1.5，φ2=-0.95,δ=0.5时，EWMA残差控制图的平均运行长度ARL=22.6026是传统残差控制图ARL=157.8806的七分之一；自相关残差控制图与EWMA残差控制图相比较:当φ1=1.5，φ2=-0.95,δ=2.0 ，EWMA残差控制图的ARL=3.0517较自相关残差控制图的ARL=3.0732小，可见，虽然差距不是很明显，但EWMA残差控制图可以提高对中小漂移的检测效率。

但是当φ1+φ2-φ22＞0时，自相关残差控制图和EWMA残差控制图的检测效率较传统残差控制图逐渐变弱，即传统残差控制图不受参数取值的影响，其表现结果都一致的好，而当φ1+φ2-φ22＞0时，自相关残差控制图和EWMA残差控制图检测效率偏慢。

在实际生产中，数据都是存在自相关性的，那么残差必会受到相关系数的干扰。这时如果使用传统残差控制图检测时可能会产生更多的虚发警报，而自相关残差控制图和EWMA残差控制图是考虑到相关系数对均值漂移值的影响进行的检验。根据表1，当φ1+φ2-φ22＜0时，自相关残差控制图和EWMA残差控制图，检测效果一致的好；同时，无论φ1+φ2-φ22＜0和φ1+φ2-φ22＞0时，EWMA残差控制图都要比自相关残差控制图效果还要好。

4 结束语

本文通过自相关过程的EWMA残差控制图的设计与实验模拟,证明了该控制图提高了针对自相关过程发生中小漂移检测的灵敏度；虽然之前在AR(1)上讨论EWMA控制图对中小漂移检测效率很高，但是并没有系统给出自相关过程的检测漂移能力强弱的判断方法。综上所述，本文提出的方法应用到实践，可以提高检测效率带来实际的经济效益，为了进一步提高检测效率，还可以考虑基于似然比统计量的控制图。