文氏图在计量统计类课程教学中的应用——以多重共线性内容为例

陈 军

（新疆师范大学商学院，新疆 乌鲁木齐 830017）

在多元线性回归中，通常采用OLS（最小二乘法）作为估计回归模型参数的方法，但需满足若干基本假定，包括关于变量和模型的假定和关于随机扰动项统计分布的假定。其中假设之一就是解释变量间不存在多重共线性，但在实际研究中，模型中的解释变量间往往存在不同程度的共线性问题，对此情形需要进行相应的消除解决，再行应用OLS。多重共线性的内容在“统计学”“计量经济学”课程中都有涉及，也是教学中的一个重点和难点。在教学实践中，一般采用定义数学方程、矩阵等讲授，但涉及数学知识点多，理论讲解相对费时，如果学生数学基础不扎实，那么对这部分的内容理解起来就相对吃力。通过引入文氏图，可有助于这部分内容讲解和学生的理解。

文氏图属于集合论数学分支，用于展示不同集合（群组）之间的数学或逻辑关系，常被用于集合（类）运算。一般用矩形框表示论域，矩形框的内部区域即论域范围，可视为全集，即所有可能事物的空间。单个集合用圆或椭圆表示，若两个圆或椭圆相交，相交部分则是两个集合所包含的公共元素；若两个圆或椭圆不相交，则表明两集合无公共元素。需要说明的是，文氏图与其它的图示法一样，它不能准确表示一个集合（或类）中到底有哪些元素。下图为集合A, B的文氏图。

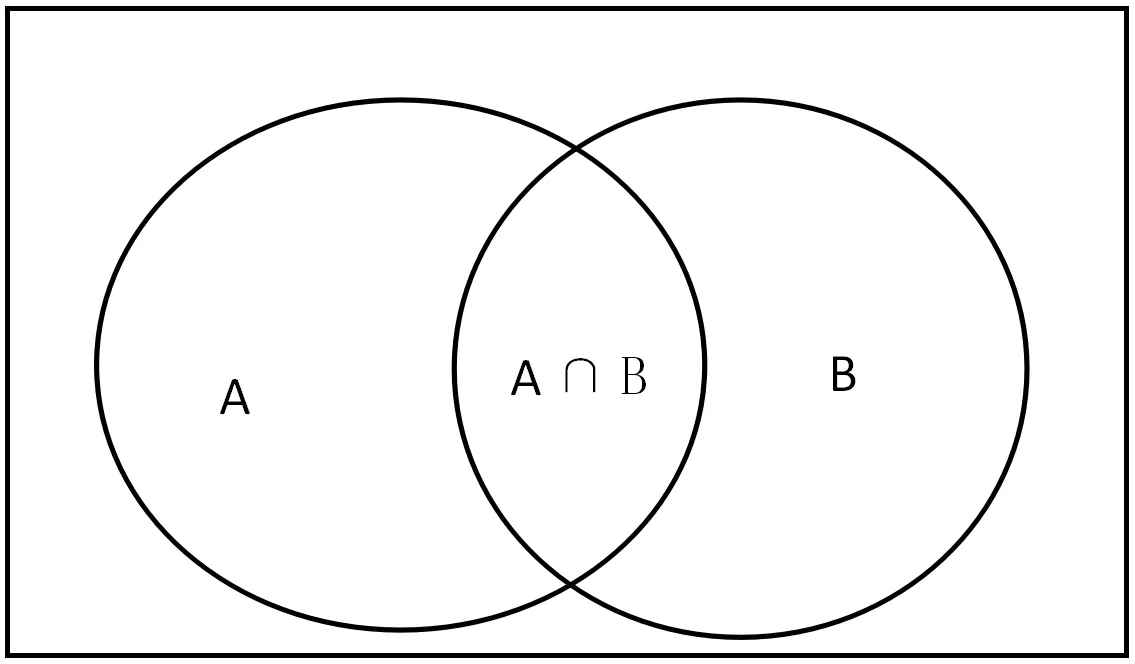
图1 集合A, B的文氏图

一、文氏图在“多重共线性”定义及分类讲解时的应用

变量λ1x1+λ2x2+…+λkxk=0之间共线性的情形有三种，分别是完全共线性、不完全多重共线性和无多重共线性。

（一）基于数学理论的多重共线性定义及分类

1.完全共线性

变量间存在完全共线性，即对于变量x1，x2，…，xk，如果存在不全为零的常数λ1，λ2，…，λk，使得下式成立：

则称解释变量x1，x2，…，xk之间存在完全共线性。

2.不完全共线性

变量间存在不完全共线性，即对于变量x1，x2，…，xk，如果存在不全为零的常数λ1，λ2，…，λk，使得下式成立：

则称解释变量x1，x2，…，xk之间存在不完全共线性，其中μ为随机误差项。与完全共线性不同的是，不完全共线性反映出变量间是近似线性关系，而非函数关系。因而，不完全共线性也称近似的多重共线性，实际经济问题的大多数情况呈现这种情形。

3.无多重共线性

无多重共线性是指解释变量x1，x2，…，xk之间，既不满足式（1），也不满足式（2）的情形。矩阵x为满秩矩阵，即rank(X)=k+1。应该注意到，解释变量x1，x2，…，xk之间不存在线性相关，并不说明不存在非线性相关。由于各解释变量x1，x2，…，xk之间往往在时间上存在同向变动趋势，且存在不同程度关联度，无多重共线性情形一般很少。

（二）基于文氏图的多重共线性定义及分类——以二元线性回归模型为例

基于文氏图的多重共线性可分三种情形：无多重共线性、不完全共线性及完全共线性，如图2所示。

1.完全共线性

假设线性回归模型有两个解释变量x1，x2，各自代表相应变量信息。若存在常数λ1，λ2，满足λ1x1+λ2x2=0，即解释变量x1，x2之间存在完全共线性。用文氏图可表示为如图2(c)，说明变量x1反映的信息和x2反映的信息，虽然形式不同，但两者信息是完全重复的。

2.不完全共线性

假设线性回归模型有两个解释变量x1，x2，各自代表相应变量信息。若存在常数λ1，λ2，满足λ1x1+λ2x2+μ=0，即解释变量x1，x2之间存在不完全共线性。用文氏图可表示为如图2(b)情形，说明变量x1反映的信息和x2反映的信息，虽然形式不同，但两者信息部分是重复的。变量间相关程度越大，图形中x1，x2重复的部分越多。

3.无多重共线性

假设线性回归模型有两个解释变量x1，x2，各自代表相应变量信息。若既不存在常数λ1，λ2，满足λ1x1+λ2x2=0，也不满足λ1x1+λ2x2+μ=0，这时解释变量x1，x2之间不存在共线性。用文氏图可表示为如图2(a)情形，说明变量x1反映的信息和x2反映的信息，无交集，即解释变量x1，x2之间线性相关系数为零，各自提供的信息无重合部分。

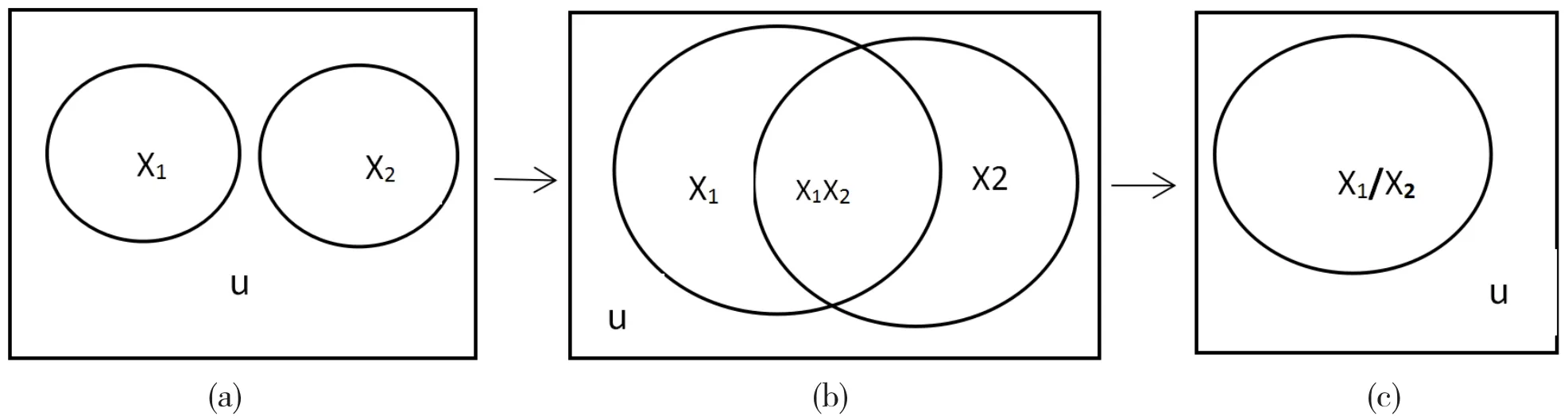
图2 共线性分类的文氏图表示

二、文氏图在讲解多重共线性检验时的应用

多元线性回归模型中，如果解释变量间存在多重共线性，但仍采用OLS方法估计模型参数，一般将产生较为严重的后果。以二元线性回归模型为例，在完全共线性情形下，参数估计量将不存在，表现在参数估计量 和 为不定式，且方差为无穷大；而在不完全共线性的情形下，则呈现出参数估计量 和

的方差、置信区间伴随x1，x2共线性程度增加而增加，同时t检验失效、预测精度降低、回归模型缺乏稳定性等影响。因此，在进行模型回归前，一般要进行多重共线性的检验，主要检验方法包括相关系数检验、F-G检验、特征值检验、方差膨胀因子（VIF）检验等。

在实际应用中，往往考虑如下方法研判：R2或其修正值很高（F值也相应高），但某些解释变量系数的t值却不显著或偏低。这时，我们就可初步判断解释变量x1，x2，…，xk之间可能存在多重共线性。这种结果看似矛盾，其实不然。F检验表明因变量与解释变量之间的线性关系是显著的，即因变量和解释变量中的一个变量间的线性关系显著，并不代表和每个解释变量之间的线性关系都显著。为了便于理解，可借助文氏图3表示。

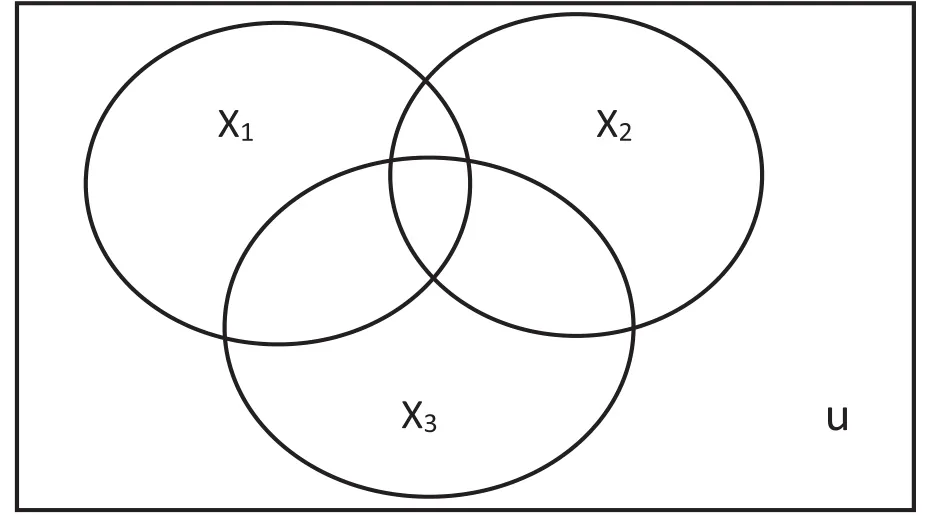
图3 多重共线性检验的文氏图表示

上图中，X1、X2、X3分别表示多元线性回归模型中三个解释变量对因变量的解释贡献度，F检验值可理解为X1、X2、X3三个集合形成的面积。由于共线性的存在，导致无法区分X1、X2、X3对因变量的具体解释贡献度，尽管单独对每个解释变量回归，系数呈现显著性。某些解释变量的贡献度和另一些解释变量的贡献度相互重叠了。借助文氏图，对于讲授这个知识点，学生更容易理解。

三、文氏图在线性回归模型多重共线性分析的例题应用

为完整体现文氏图在线性回归模型多重共线性分析方面的应用，下面结合一个具体的案例来说明。

例：根据理论和经验分析，影响国内旅游市场收入Y的主要因素，除了国内旅游人数和旅游支出之外，还可能与相关基础设施有关。为此，考虑的影响因素主要有国内旅游人数X1，城镇居民人均旅游支出X2，农村居民人均旅游支出X3，并以公路里程X4和铁路里程X5作为相关基础设施的代表。统计数据如下表1所示。要求建立国内旅游市场收入的多元线性回归预测模型，并检测共线性情况。

分析本例题模型中的变量，公路里程（X4）和铁路里程(X5)两个变量反映的信息应有重叠，而国内旅游人数（X1）、城镇居民人均旅游支出（X2）、农村居民人均旅游支出(X3）等三个变量反映的信息应有重叠（通过相关系数矩阵也可得出），考虑模型中解释变量间可能存在共线性问题。模型中解释变量及随机误差项反映信息用图4文氏图表示。

本例以SPSS作为数据处理软件，采用逐步回归法解决多重共线性问题，实操步骤描述如下。

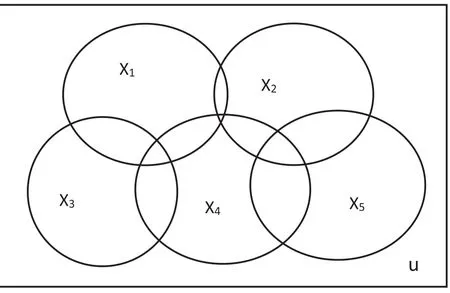
图4 解释变量及随机误差项反映信息的图示

Step1：输入数据；依次选择“分析（A）”→“回归（R）”→“线性（L）”进入线性回归对话框。在“线性回归”对话框中，将左侧框内的“Y”“X1”“X2”“X3”“X4”“X5”分别移入右侧“因变量（D）”和“自变量（I）”框内，对话框界面同前例。并在“方法”下选择“逐步”。

Step2：点击“选项”，并在“步进方法标准”下选择“使用F的概率”，并输入增加变量所要求的的显著性水平（默认值为0.05）；在“删除”框中输入剔除变量所要求的显著性水平（默认值为0.10）。点击“继续”回到主对话框。

Step3：点击“确定”。得到部分结果如表2、3。

表2 输入／移去的变量

表3 系数

上表给出了参数的估计值和用于检验的t统计量和p值。由此得到回归模型：

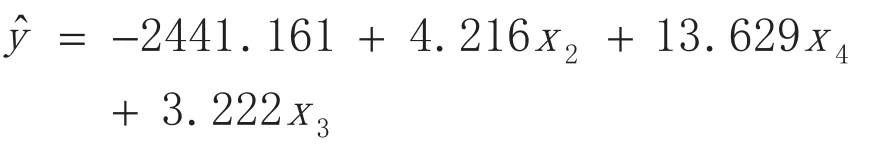
从结果可以看出，首先被选入的变量是城镇居民人均旅游支出（X2），后依次选入的变量是公路里程（X4）和农村居民人均旅游支出(X3），即在消除共线性的情形下，剔除了变量X1和X5。从经济意义解释，就是公路里程（X4）信息更多涵盖铁路里程(X5)，城镇居民人均旅游支出（X2）和农村居民人均旅游支出(X3）反映的信息更多涵盖国内旅游人数（X1），用文氏图可表示为图5。

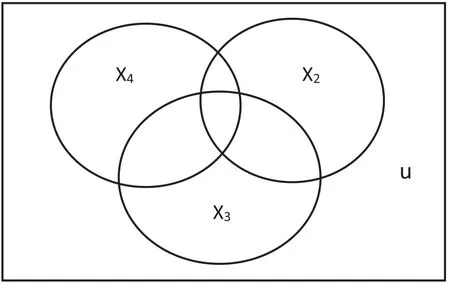
图5 回归模型变量间文氏图

四、结束语

通过上文分析，可以看到文氏图在多重共线性内容讲授时的优点，主要体现在多重共线性定义及分类、共线性检验及回归结果分析上。通过借助文氏图，可有效提高教师的教学效果和学生对此内容的理解掌握。