管制扇区交通指标的混沌特性分析

冯 程 ，刘姝含 ，巩 倩

（1.中国电子科技集团公司第二十八研究所，南京 210007；2.江苏省产业技术研究院，南京 210000；3.中国民用航空江苏空管分局，南京 211113）

空中交通系统是一个涉及航空器、空域、机场、管制员、飞行员等众多影响因素的非线性系统。近年来对空中交通系统的复杂性研究已卓有成效，逐渐提出了交通复杂性、空域复杂性、动态密度、管制复杂性、认知复杂性等多个具体概念和评估方法。而作为非线性科学的另一重要主题——混沌，在空中交通领域却较少被人提及。

目前，对混沌特性的研究主要集中在地面交通领域。郭敏等[1]利用关联维数分析发现城市快速路交通系统中存在混沌态；廖荣华等[2]发现北京交通流数据的最大Lyapunov指数约为0.045；张宏立等[3]也利用城市交通流数据检验了混沌特性；罗婷[4]证明了美国洛杉矶交通流数据中存在混沌现象。在空中交通领域，虽然相关研究成果较少，但Li等[5]也证明了空管领域中飞行冲突时间序列存在混沌现象。以国内某区域管制中心多个扇区样本为例，借鉴混沌特性检验方法，首先利用互信息法和伪最近邻点法分别计算时间延迟和嵌入维数，确定重构时间序列相空间的重要参数；然后以典型的交通运行指标为例，选用小数据量法，计算指标时间序列的最大Lyapunov指数，以此作为判断混沌特性的依据。研究结论可用来进一步挖掘交通流特性，提升交通行为的可预测性。

1 混沌特性分析方法

混沌是一种貌似无规则的、类似随机的现象，实则为一种有序结构，是内部层次十分丰富的非线性存在形式[6]。定量判断混沌特性的常见方法有：最大Lyapunov指数法、关联维数法、功率谱法等。混沌运动的基本特点是在初始条件下轨迹在时间轴上按指数形式进行分离。Lyapunov指数是相空间轨迹（即相空间中所有点的集合）收缩或扩张的标志性指标，在其为正的方向上轨迹分离，对初始条件敏感；在其为负的方向上轨迹收缩，对初始条件不敏感，运动稳定。在Lyapunov指数谱中，最小Lyapunov指数λmin决定了相空间轨迹的收缩速度；最大Lyapunov指数λmax表征两相邻轨迹的发散问题，即覆盖整个吸引子的快慢；若λmax＞0表示轨迹指数分离，则系统一定存在混沌特性。选择最大Lyapunov指数方法，通过将时间序列重构一个拓扑等价的相空间，分析吸引子的混沌特性。

根据混沌特性分析方法，首先确定时间序列的时间延迟和嵌入维数，对扇区交通指标时间序列完成相空间重构后，选取小数据量法计算最大Lyapunov指数，从而判断机场交通行为中是否存在混沌现象。

1.1 相空间重构

相空间重构是根据有限的数据来重构吸引子以研究系统动力行为的方法，是研究混沌时间序列的核心[7]，其关键在于确定时间延迟τ和嵌入维数m。

1.1.1 时间延迟

若时间延迟τ取值较小，则相空间矢量X（t）={x（t），x（t+ τ），x（t+2τ），…，x（t+（m-1）τ）}中任意两个分量 x（t+jτ）和 x（t+（j+1）τ）的数值大小会非常接近以致无法区分；若时间延迟τ取值较大，则两个分量很有可能完全独立，混沌吸引子的轨迹在两个方向上的投影毫无相关性可言。综合考虑，选用互信息法确定时间延迟。假设 S={s1，s2，…，sn}和 Q={q1，q2，…，qn}是离散信息序列，S和Q的平均信息量分别为

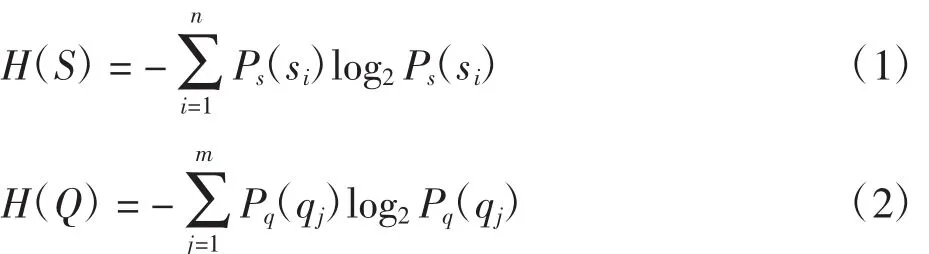
其中：Ps（si）为在S时间序列中si出现的概率；Pq（qj）为在Q时间序列中qj出现的概率。

S和Q的互信息为

定义[s，q]=[x（t），x（t+ τ）]，s表示时间序列 x（t），q 表示延迟为 τ的时间序列 x（t+ τ），则 I（S，Q）=I（x（t），x（t+ τ））表示在已知 x（t）的情况下，x（t+ τ）确定性的大小。当I（S，Q）=0时，表示x（t+τ）完全不可预测，此时x（t）与x（t+τ）完全不相关；I（S，Q）取极小值时，表示x（t）与x（t+τ）为最大可能的不相关。取I（S，Q）得出第1个极小值的τ作为最优时间延迟[8]。联合分布概率的计算步骤详见文献[9]。

1.1.2 嵌入维数

根据原有的时间序列恢复其在高维相空间中的运动轨迹，即重构相空间以甄别邻近点的真假，从而确定嵌入维数m[10-14]。在m维相空间中，每个相点X（t）={x（t），x（t+ τ），x（t+2τ），…，x（t+（m-1）τ）}，都存在某个距离内的最近邻点XF，其距离为Rm（t）=‖X（t）-XF（t）‖。当相空间的维数从m维增加到m+1维时，两个相点的距离发生变化，即

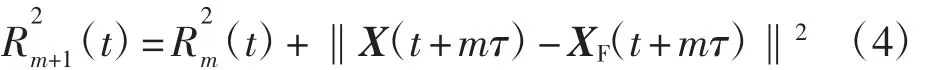
如果Rm+1（t）与Rm（t）相比变化较大，则可认为其是伪最近邻点，令

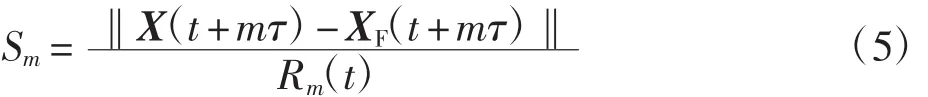
若Sm＞ST，则XF（t）是X（t）的伪最近邻点，阈值ST取值范围为[10，50][10]。

从小到大，根据不同的嵌入维数计算伪最近邻点比值，当该比值不再随嵌入维数m的增加而减少时，则可得到最佳嵌入维数。

1.2 最大Lyapunov指数

计算最大Lyapunov指数通常可以利用Wolf法、Jocobian法、小数据量法、P范数法等[14-16]。其中小数据量法对时间序列的噪声具有较强的鲁棒性，适合小数据组，计算简单，容易实现，因此选择该方法计算最大Lyapunov指数，具体步骤如下。

1）通过傅里叶变换，计算时间序列的平均周期P[15]。

2）根据重构后的相空间矢量 X（t），t=1，2，…，M；M=N-（m-1）τ，确定相空间中每个点 X（t）的最近邻点，并限制其短暂分离，即

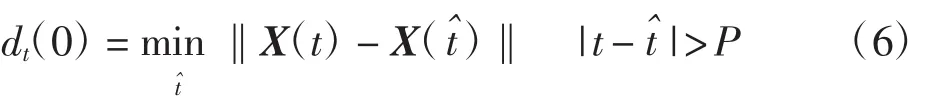
3）针对相空间中每个点X（t），计算该邻域点对i个离散时间步后的距离

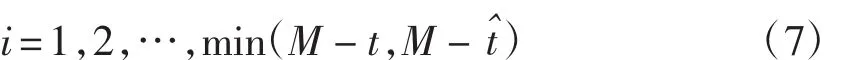
4）对每个i求出所有t的ln dt（i）的平均x（i），即

其中：q为非零dt（i）的数目。

5）选择一段线性区域作为计算最大Lyapunov指数的区域[15-16]，用最小二乘法求得该直线的斜率即为最大Lyapunov指数。

2 实例分析

扇区是空域的基本组成单元之一，管制员会向扇区内的航空器提供管制服务，通常根据空域结构和流量分布将空域划分成多个扇区以便管理。选取国内某区域管制中心10个扇区作为分析对象。参考已有研究成果，选取反映扇区交通特征的指标主要包括：航空器数量、总管制里程、平均管制里程、总管制时间、平均管制时间、爬升航空器数量、平飞航空器数量、下降航空器数量、改变航向的航空器数量、改变速度的航空器数量、改变高度的航空器数量、平均速度、水平最小间隔、垂直最小间隔、追越冲突航空器对数量、对头冲突航空器对数量。

选取某天的历史运行数据用于指标计算，以1 min为间隔，构造所有扇区在各指标下的时间序列。首先对所有指标时间序列完成相空间重构，然后基于小数据量法计算最大Lyapunov指数，检测扇区交通运行特征中的混沌特性。

以扇区1的航空器数量指标为例，分别得到互信息与时间延迟的变化关系以及伪最近邻点比例与嵌入维数的关系，如图1～图2所示。

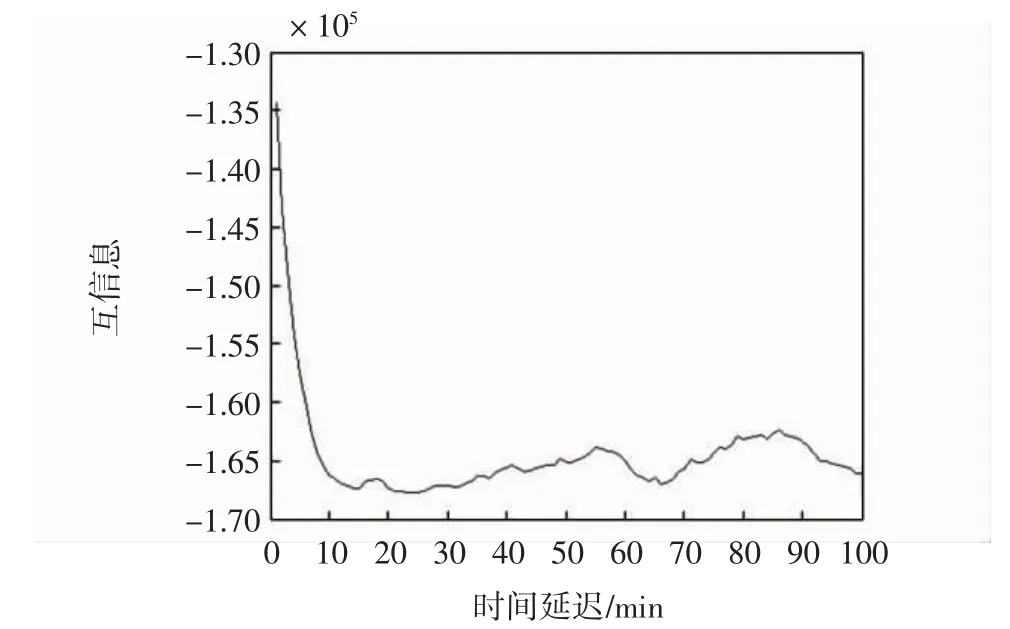
图1 时间延迟与互信息的变化关系Fig.1 Relationship between time delay and mutual information

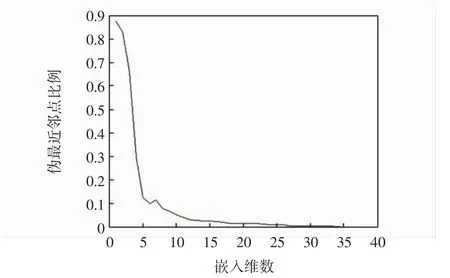
图2 嵌入维数与伪最近邻点比例的变化关系Fig.2 Relationship between embedding dimension and pheudo nearest neighbor ratio

由图1可知，当时间延迟τ=14时，自信息获得第1个极小值；由图2可知，当嵌入维数m=35时，伪最近邻点的比例降为0，由此确定时间延迟和嵌入维数。扇区1航空器数量时间序列的最大Lyapunov指数是0.06，因此扇区1的交通运行存在混沌特性。

所有扇区部分指标的最大Lyapunov指数计算结果如表1所示。

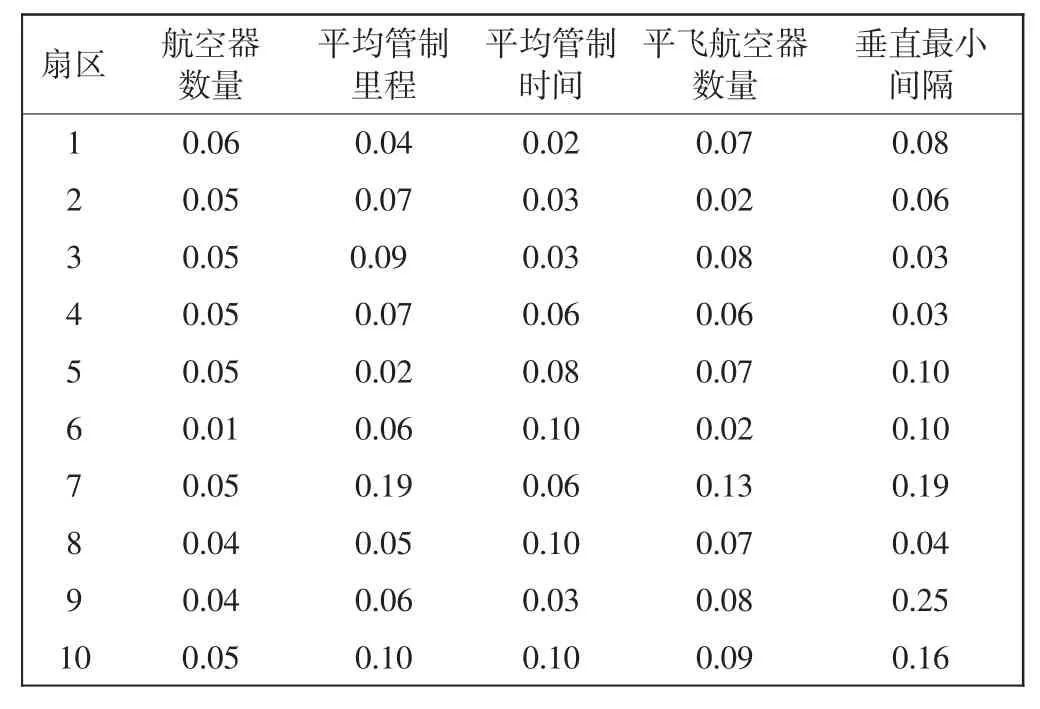
表1 部分指标最大Lyapunov指数计算结果Tab.1 Calculation results of maximum Lyapunov exponent of some indicators

基于10个扇区、16个指标的最大Lyapunov指数计算结果显示，对于所有扇区样本，共有5个指标（航空器数量、平均管制里程、平均管制时间、平飞航空器数量、垂直最小间隔）的时间序列具有大于0的最大Lyapunov指数，因此在表1中仅展示这5个指标的计算结果。这5个指标涉及了交通运行的各个方面：航空器数量反映了扇区内航班的整体分布水平，平均管制里程与平均管制时间则从另一个角度反映了航班的平均分布水平；平飞航空器数量反映了区域扇区内航班处于平飞状态的分布水平；垂直最小间隔反映了航班之间的耦合状态，航班之间垂直间隔越小，潜在冲突可能性越大。上述5个指标容易观察、发生频率高，因此只要各时间片内存在运行的航空器就能观测到指标值。其他指标的统计结果目前还不具备较强的一致性：仅有少量扇区样本的爬升航空器数量出现了最大Lyapunov指数大于0的情况；对于总管理里程和总管制时间，大部分扇区样本的最大Lyapunov指数大于0，少量扇区可能由于样本数据缺失，导致计算结果并不理想；而对于追越冲突航空器对数量和对头冲突航空器对数量两个指标，由于本身出现的概率较小，大部分时间片内数值几乎为0，故混沌特性检验结果也不明显。

由于目前仍缺乏航班运行历史数据，因此相关结论的普适性也需要深入论证，今后应进一步收集全国扇区的运行数据，继续统计各类指标计算结果，检测扇区交通指标的混沌特性。扇区复杂性与拓扑结构、运行条件（空域管制）、人为因素（管制人员级别、经验水平）、气象条件等一系列因素息息相关，扇区交通行为也非常复杂。有序的交通流在各种非线性因素的多重干扰下，交通态势逐渐呈现出非线性特征，扇区交通运行的内在随机性也大大增强，最终产生了混沌特性。

3 结语

空中交通系统是一个复杂的非线性系统，不同指标所反映的运行特征中均存在混沌特性。深入分析空中交通系统内的混沌特性，对于进一步完善空中交通流的非线性特性以及实现对交通的准确预测和控制具有重要的现实意义。利用实际运行数据，明确了扇区运行中普遍存在混沌现象的5个交通特征：航空器数量、平均管制里程、平均管制时间、平飞航空器数量及垂直最小间隔，通过以上特征指标可进一步量化评估扇区运行的内在规律。长期以来，管理者一直认为交通行为是无序的，故难以对其进行准确预测。而以上结论则为管理者提供了一个新的解决思路。目前，关于混沌时间序列的预测方法日渐成熟，根据建模数据可分为3类，包括全局预测、局部预测和自适应预测。每种方法都有不同的适用对象，其预测精度也与时间序列、预测时间范围密切相关。因此，对于交通运行特征存在混沌特性的扇区，应收集相关历史数据，建立基于混沌特性的扇区交通行为预测模型，提升交通行为的可预测性，从而预判扇区内可能出现的复杂交通态势，提前制定管控措施，大力提升运行效率。