离港飞机滑行路径优化与仿真

邢志伟 ，徐铭怡，罗 晓 ，罗 谦

（1.中国民航大学电子信息与自动化学院，天津 300300；2.中国民航局第二研究所信息技术分公司，成都 100142）

随着中国航空业的快速发展，航空流量密度迅速增大，又因机场地面资源、跑道、滑行道和停机位等条件限制，导致地面滑行过程中发生冲突的热点区域增多，引起航班延误与机场场面交通拥堵等现象，影响了航空运输业的正常发展。在空域资源短缺、机场扩张受限、机场基础设施有限等情况下，优化可变滑行时间以充分利用现有资源成为解决航空流量密度大时机场场面交通拥堵及航班延误等问题的首要选择。相关研究中，李楠等[1]采用A*算法得到使总时间最短的滑行路径以提高机场场面运行效率。谷润平等[2]使用改进后的D*算法，动态预测飞机的滑行路径，缓解了机场场面交通拥堵现象。Lee等[3]提出以离港延迟的航班罚函数和以最短滑行时间为目标去优化滑行距离的MILP模型。Levy等[4]利用机场场面监视数据得到各跑道、滑行道的利用率完成对飞机滑行时间的预测。钟石泉等[5]提出核心路径法，构建具有能力限制与距离限制的数学规划模型，实现了离场滑行目标路径规划。仉俊峰等[6]利用图论的方法解决了从起点到终点寻找最优路径的策略。综上所述，国内外在机场场面有限的条件下，对缓解机场场面交通压力方面的研究取得了一定成果，但现有的离港飞机滑行路径优化算法未能充分考虑实际滑行问题中等待时间的情况，未能有效解决提出的问题。

针对机场条件限制、机场场面交通压力大等关键问题：首先，研究智慧机场高效运行的考察指标；其次，通过优化航空器滑行时间来提高整体协同决策，缩短多架飞机从停机位到跑道端口前之间的可变滑行时间，对飞机离港的滑行路径进行优化[7]；最后，提出基于元胞自动机的方法对机场场面拓扑建模，并利用改进的蒙特卡洛算法对所建模型进行求解[8]。

1 机场场面元胞自动机模型建立

通过分析机场场面特性，根据元胞传输自动机基本理论，利用有向网络拓扑图的结构布局，依据民航场面滑行标准将机场场面分为以下3部分交通流运输模型。

1.1 一般滑行道元胞模型

飞机在停机位和跑道之间根据分配好的路径进行滑行，如图1所示。在第t+1时刻元胞i的存量可表示为

其中：qi-1（t）为元胞i-1的流出流率；qi（t）为元胞i的流出流率；Ni（t）为元胞i的存量；dT为单位仿真时间步长。

图1 一般滑行道元胞传输Fig.1 Cell transfer on general taxiing path

根据元胞特性可知，下游元胞可接受的流量和元胞的自身流量会约束上游元胞的流出量。上游元胞流出量qi-1（t）dT计算为

其中：li-1为元胞i-1长度；为元胞i-1的平均速度；Ci为元胞i容纳飞机的最大数量，即

式中：pij是前机型为i、后机型为j的概率；Dij是前机型为i、后机型为j的安全间隔规定。

同理可计算qi（t）dT。

1.2 机坪元胞模型

将机坪元胞设定为离港飞机机坪元胞，由于在离港元胞与进港一般滑行道元胞之间存在交点，会使机场场面更为复杂，如图2所示。

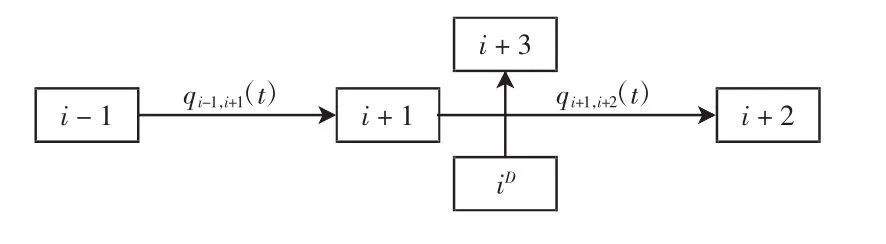
图2 机坪元胞传输Fig.2 Apron cell transfer

机坪离港元胞iD在时间片内的最大流出量、第i+1个元胞的最大流出量及飞机推出量分别表示为

1.3 汇聚元胞传输模型

由于飞机推出后沿着滑行道滑行至跑道端头时，离港交通流会在跑道和滑行道的交汇口产生汇聚，如图3所示。

图3 汇聚元胞传输Fig.3 Cross cell transfer

假设元胞i所能接收的流量为Ri（t）=Ci-Ni（t）；元胞i-1所能传输的最大流量为li-1；元胞i-2所能传输的最大流量为Si-2，i（t）=Ni-2（t）×元胞i-1和元胞i-2的流量为

其中，βi-1（t）、βi-2（t）为第t时间步长内上游元胞i-1和元胞i-2存量所占的比例，即

1.4 约束条件

1）跑道约束 每个离港航班必须分配且只能分配一条跑道，即

其中：φ=|R|为跑道数量；R为跑道集合；当航班i进港时分配到跑道r时，pir=1，否则pir=0。

2）停机位约束 每个离港航班必须分配且只能分配一个停机位，即

其中：m=|G|为可用停机位总量；G为可用停机位集合；当把航班i分配到停机位k上时，yik=1，否则yik=0。

3）最小间隔约束 离港飞机在机场场面滑行过程中必须满足一定的安全间隔。定义0-1决策变量对航空器进行位置识别，即航班f在t时刻到达j节点，需使用的最小间隔约束定义为

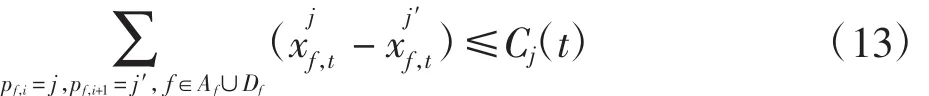
其中：Af为进港航班集合；Df为离港航班集合;依据管制原则，每架航班都有一个由一系列的节点pf构成的优选路径集合Pf，从而pf∈Pf；设某起点j的滑行道的滑行链路长为L，最小间隔规定为D，Cj=「L/D」表示起点为j的链路容量。

4）超越限制约束 若前慢后快的2架航班连续进入某一具有高容量值的滑行道，需满足先进先出的原则。在一条滑行道链路的实际运行中不可能出现允许速度快的航班超越速度慢航班的情况。因此，所采用的方法是将超越限制约束转化成容量限制约束，即将各链路的容量值设为1，有Cj（t）=1，这样就使得2架航班不可能同时出现在一条链路中。对于容量大于1的滑行道链路，可人为添加节点，也可满足每条链路的容量不大于1，又可提高运行效率[9]。

2 蒙特卡洛算法优化求解

2.1 随机数的生成

蒙特卡洛算法是一类基于概率论处理方法，可用来对非线性和离散系统进行后验概率分布的估计，具体可描述为：通过一组依据重要性采样得到的带有权值的样本集合来估计研究对象的未来概率分布，样本会进行周期性的数据更新[10]。在预测阶段，首先对已知的机场数据进行初始化，根据机场交通流运输模型对机场交通进行算法预测；在滤波更新阶段，滤除不符合机场模型的样本数据，然后对数据进行二次筛选，筛除不满足机场模型约束条件的数据，获取机场元胞模型的数据；最后对机场进离港流量分析。仿真流程如图4所示。

图4 仿真流程Fig.4 Simulation procedure

在对已知分布进行采样的过程中，随机数被看作已知量[11]。乘同余法是一种典型的计算机伪随机数生成方法。其实现形式是：对于任一初始值xi，以下可得到伪随机数序列 ξi，即

其中：x0为随机种子，即初始值；a为乘子；M为模数。

2.2 蒙特卡洛优化求解的实现

首先将连续时间分割为离散的时间单元t，ot表示接收到的元胞观测信息，lt表示在t时刻的位置状态情况；用以表示前一个t-1时刻的位置情况来预测当前t时刻位置情况的方程p（lt|lt-1），称为状态转移方程；用以表示位置信息位于lt的概率方程p（lt|ot），称为观测方程[12]。

第一阶段 预测阶段。飞机滑行的元胞自动机模型最大速度Vmax已知，假设lt-1为t-1时刻的样本，则t时刻的位置信息lt是以前一时刻的位置信息lt-1为起点，以飞机滑行允许的最大滑行速度Vmax所处的位置点为终点的线段上任意一点。d（lt，lt-1）表示两点之间的实际距离。假设滑行过程服从均匀分布[0，Vmax]，由此状态转移方程为

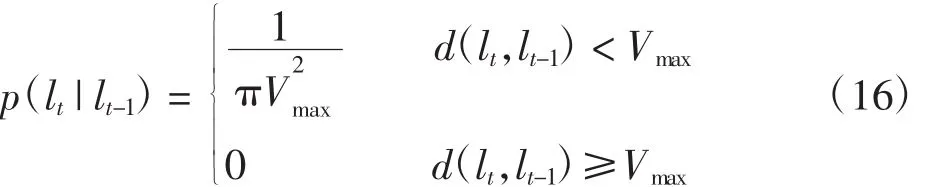
第二阶段 过滤与更新阶段。因为元胞自动机模型的设定，飞机的滑行只能以元胞为单位进行位置更新，可更新的位置信息用S来表示，每个位置的可运动长度为 r，可得到当满足条件 d（lt，s）≤r时保留，否则被过滤掉[13]，其中 s∈S。

第三阶段 序列重要性采样阶段。重要性采样的核心是找到一个概率分布已知、容易采样且与样本有相似概率分布的重要性函数q[14]。在蒙特卡洛算法中，重要性函数q设定为状态转移方程p（lt|lt-1），则预测下一时刻t的位置信息为

对以上权值进行标准化处理后可得到

其中，在蒙特卡洛算法的定位过程中，N通常设定为采样的最大值Nthreshold。

3 滑行路径模型仿真与分析

3.1 实验数据来源与分析

用于实验的网络拓扑和数据来源于国内某大型枢纽机场的布局结构和实际运行数据，局部网络拓扑图如图5所示。

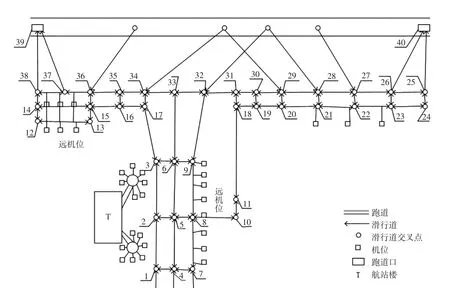
图5 国内某大型枢纽机场局部网络拓扑Fig.5 Partial network topology of one domestic hub airport

用于实验分析的数据选取该机场在2017年1～3月的生产数据，统计计算后可知平均每架飞机所用的平均滑行时间约为21.39 min。选取这3个月实际运行数据中的某一天从各停机位推出的航班总架次为762架。为便于分析研究，规定以每15 min的时间间隔为一个时隙，在07：00至22：00这15 h的繁忙时段内，离港航班平均11.75架/15 min；当日的空闲时段内，离港航班平均0.42架/15 min。

3.2 仿真结果对比

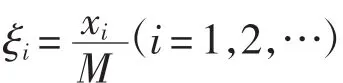
各停机位在每一个时隙都会相继推出新的航班，进入滑行道系统的离港航班会逐渐增加，离港需求也会产生积累，造成航班之间的滑行冲突。为避免滑行冲突的产生，同时也为了验证模型的有效性，利用蒙特卡洛算法在对模型进行计算时需满足最小间隔约束条件，此条件的成立可通过蒙特卡洛优化算法中状态方程进行监控。

从停机位推出的航班将会从1、2、3这3个滑行道节点进入滑行道系统，分别对从这3个节点进入滑行道的航班进行分析仿真。依据管制中心为航班分配的滑行路径与运用建模仿真后的滑行路径为离港航班重新生成滑行道滑行时间，通过比较仿真结果与实际运行数据后得到3个节点的滑行时间对比，如图6、图7和图8所示。

图6 从1号节点进入滑行道的航班滑行时间Fig.6 Taxiing time of flights from Node 1

图7 从2号节点进入滑行道的航班滑行时间Fig.7 Taxiing time of flights from Node 2

图8 从3号节点进入滑行道的航班滑行时间Fig.8 Taxiing time of flights from Node 3

运用元胞自动机分模块建模后使用蒙特卡洛算法优化求解，离港飞机的平均滑行时间从21.39 min降低至19.27 min，滑行效率平均提升了9.9%，总的滑行时间降低至407.04 min。除个别航班的滑行路径优化效果不明显外，整体航班滑行时间在优化滑行路径后，地面滑行时间有所减少，对于滑行时间高于均值的航班优化效果更为显著，有效地避免了地面滑行道的拥堵，可为离港航班选择尽量最优的滑行路径，使其尽快到达跑道端头等待起飞。

4 结语

首先，针对飞机在地面滑行过程中产生冲突的热点区域逐渐增多、造成航班延误与机场场面交通拥堵加剧的问题，提出了对飞机离场路径进行优化的必要性；其次，针对国内某大型机场，根据机场场面特性利用元胞传输自动机原理建立机场场面离场交通流数学模型；最后，通过对蒙特卡洛算法的优化，对建立的机场场面交通流模型进行求解，利用实际机场运行数据对模型进行仿真验证。对滑行路径重新优化后，能减少可变滑行时间，相比于机场现行的滑行路径方式，其在每个时隙内的滑行流畅度、平均离港滑行时间和机场通行量等各方面都体现出极大的优越性。从而缓解了高峰时段内机场的交通拥堵，平衡滑行道负载，高效利用滑行道系统，均衡机场场面交通流，进而减少航班延误，达到为机场运行提升工作效率、节约经济成本、减少环境污染和提高旅客满意度的目的。