面向控制到达时间的巡航飞行剖面实时优化

洪网君，汤新民，陈 平，顾俊伟

（1.南京航空航天大学民航学院，南京 211106；2.中国电子科技集团公司第二十八研究所，南京 210007）

在航空器实际运行中，很多因素都会对其运动状态产生影响，由此导致实际飞行状态可能与预战术阶段规划的航迹并不相符。如高空大气环境的扰动或自动相关监视设备观测到飞行冲突，必须及时对当前的飞行操纵做出相应调整，这种扰动或调整将使航空器偏离初始4D航迹，产生较大的到达时间误差。而现有的到达时间规整算法大多针对预战术阶段的4D航迹，难以满足航空器实时的飞行要求。因此，基于航空器动力学模型和外界气象条件，在融入航空器性能约束的前提下，通过设定优化指标函数并结合预计到达时间（ETA），给出航空器速度剖面的优化结果。由此获取航空器到达目标航路点的控制到达时间（CTA），实现真正意义上的4D航迹引导。

航空器在全部飞行过程中，绝大部分是处于巡航状态，因此提出一种面向控制到达时间的巡航阶段飞行剖面实时优化方法，以提前获知的预计到达时间作为约束条件，航空器油耗最少作为优化目标函数。动态优化航空器的空速加速度来调整速度剖面，修正到达时间误差，使航空器在规定时间节点通过目标航路点。

1 巡航飞行剖面实时优化模型

1.1 目标函数建立

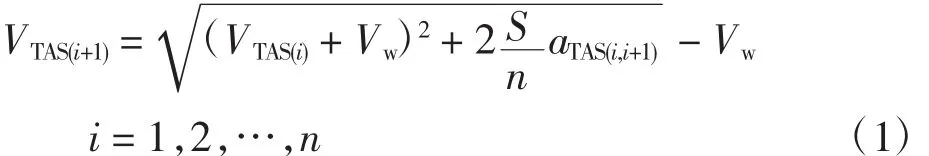
其中：VTAS(i)为 Pi均分点对应的真空速度（m/s）；Vw为风速（m/s），暂且仅考虑航空器的顺逆风飞行；aTAS(i，i+1)为PiPi+1均分段对应的真空加速度（m/s2），在风速固定的情况下，即航空器在该均分距离内的地速加速度[2-3]。因此，航空器在PiPi+1均分段飞行时间为

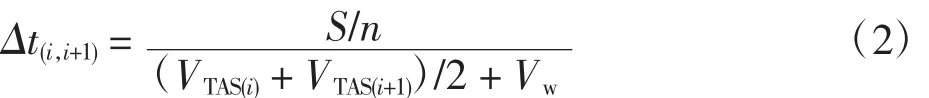
航空器在飞行距离P1Pn+1的全部飞行时间为

将性能优化目标minW写成离散形式，即

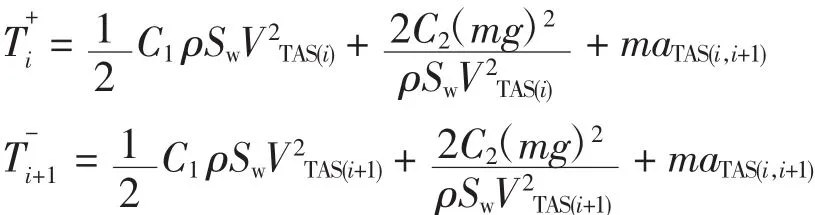
其中：Sw为航空器机翼面积（m2）；C1为零升阻力系数；C2为诱导因子；ρ为航空器所在飞行高度的大气密度（kg/m3），具体计算公式参见文献[4-5]；m为航空器的质量；g为航空器的重力加速度，一般取9.8 m/s2。

1.2 约束条件

外界环境扰动结束后，航空器的剖面优化初始速度VTAS(1)已通过相应的空地数据链下传，可视为已知量，且在航空器空速的稳态范围之内，即

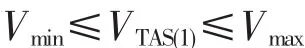
其中，Vmax、Vmin分别为航空器在该巡航高度内的最大和最小巡航速度。对于B737-800飞机，最大巡航马赫数0.82 M。

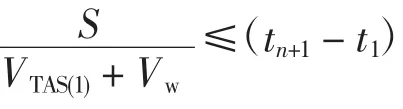
1）速度约束

2）推力约束

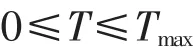
其中，Tmax为发动机在巡航高度所能产生的最大推力，即

其中，CTc1、CTc2、CTc3为第一、第二、第三推力系数；HCR为航空器的巡航高度（ft，1 ft=0.3048 m，下同）。

3）加速度约束

为保证推力约束，空速加速度上界amax和下界amin分别表示为

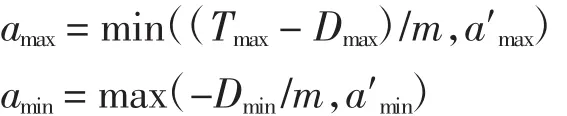
其中：a′max和 a′min分别为 BADA 性能数据库[6]给出的空速加速度最大值和最小值，即通过调整空速加速度变化范围来满足推力约束条件；Dmax和Dmin分别为阻力的上界和下界，即

式中，D为航空器在飞行过程中受到的空气阻力，即

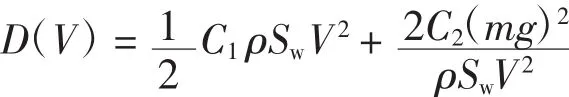
4）时间约束

为提高优化速度、改善优化效果，对时间约束适当放宽至允许的误差范围内，即

其中，t′为一个特定的阀值，即优化飞行时间在所设定的允许误差范围之内，可实现航空器4D航迹引导。

2 基于改进遗传算法的飞行剖面优化策略

2.1 编码方式

上述提出的优化问题涉及到n个变量，如果采用传统的二进制编码方式必须进行频繁的编码和解码，计算量较大。因此，采用实数编码，无需编解码操作，减少串码长度，提高遗传算法的搜索效率。实数编码是指个体的每个基因值用某一范围内的一个实数来表示，个体的编码长度等于其决策变量的个数。

2.2 适应度函数

在遗传算法的应用中，对约束条件可采用罚函数法进行处理[8]。

若优化前已大致判断出航空器需要加速飞行，则速度约束条件退化成VTAS(n+1)≤Vmax，则增广目标优化函数 minW′为

否则VTAS(n+1)≥Vmin，增广目标优化函数minW′为

其中，d1、d2为惩罚系数，取正值，针对不同的优化问题需要动态调整。因此，适应度函数为

2.3 优化策略

1）选择策略

选择策略是用来确定如何从父代群体中选取个体遗传到下一代群体。其主要目的是避免基因缺失、提高全局收敛性和计算效率。用轮盘赌的选择方法来进行个体选择，将每个个体的适应度占总适应度的比例作为该个体被选择的概率。

2）交叉策略

算术交叉是指由2个个体的线性组合而产生出2个新的个体。将 2 个个体 ax=[ax(1)，ax(2)，…，ax(n)]和 ay=[ay(1)，ay(2)，…，ay(n)]进行线性组合，得到 2 个新个体为的一个随机数。

3）变异策略

均匀变异分别用符合某一范围内均匀分布的随机数，以某一较小的概率来替换个体编码串中某个基因位上原有的基因值。选择第x个体ax=[ax(1)，ax(2)，…，ax(n)]的第k个基因位ax(k)进行变异操作，则变异后的基因位为：a˙x(k)=amin+c（amax-amin）。其中：c∈[0，1]的一个随机数；amax和amin分别表示在该基因位上所能取到的最大值和最小值。

4）最优个体保存策略

最优个体保存策略是指当代种群中适应度最高的个体不参与交叉、变异，而是用其来替换本代群体中经过交叉、变异等遗传操作后，所产生的适应度最低的个体。可看出，每代群体中最优个体以概率为1遗传到下一代。有助于提高收敛速度，避免陷入局部最优。

5）基于爬山法的局部寻优策略

爬山法首先在搜索空间随机选取一点作为进行迭代的初始点，然后在其邻域内随机产生一点，计算其适应度值。若该点适应度值高于当前点，则用该点作为新的初始点继续在邻域内搜索，否则继续在邻域随机产生另一个点与初始点进行比较，直到找到比其优秀一点，如连续几次都找不到比其优秀的点则终止搜索过程。利用爬山法可对每次交叉和变异产生的个体进行局部寻优，通过该方式调整遗传算法的进化方向，提高遗传算法的收敛速度[9]。

6）终止条件

达到最大迭代次数或连续10代群体中的最优值变化稳定在10-2以内，则视为满足终止条件，终止算法，获得最优解。详细优化流程图如图1所示。

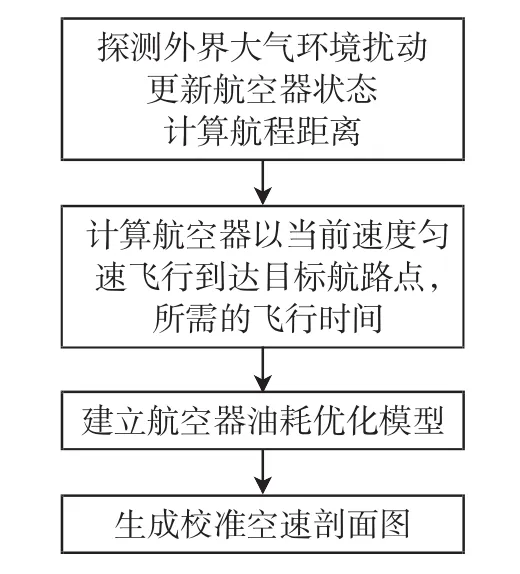
图1 优化流程图Fig.1 Optimization flow chart

3 案例仿真与分析

以某架B737-800飞机为例，标准大气环境，航空器巡航高度29000 ft。可参考BADA性能数据库，相关参数如表1所示。

设航空器在巡航高度29000 ft受到某种外界大气环境的剧烈扰动，扰动结束后，剖面优化的初始真空速VTAS(1)已通过空地数据链下传，为390 kn（200 m/s）。航空器的最大巡航速度为0.82 M，航空器预计飞行距离S=202550 m。

表1 性能参数表Tab.1 Performance parameters

图2为风速Vw=0，给定飞行时间900 s，利用传统遗传算法和改进遗传算法进行优化的增广目标函数迭代曲线图。

图2 基于不同遗传算法的增广目标函数迭代曲线图Fig.2 Augmented objective function iterative curve based on different genetic algorithms

从图2可知，基于改进遗传算法的优化油耗收敛很快，进化45代时就趋于收敛状态，但基于传统遗传算法的优化油耗收敛很慢，进化代数达到100仍未收敛。可见，基于爬山法的改进遗传算法可有效转变遗传算法进化方向，减少优化时间，提高优化速度。

图3和表2为风速Vw=0，在不同飞行时间下，利用改进遗传算法进行优化的校准空速随航程距离变化剖面图及优化性能参数表。

由图3和表2可发现，预计飞行时间会影响校准空速剖面图。随着预计飞行时间的变长，校准空速剖面图近似为一条直线，即校准空速随航程线性变化。对于t=880 s，由于其数值过小，据文献[10]可知，需在优化的初始端施加一个较大的加速度，才能在规定时间到达目标航路点。飞行时间也会影响油耗，虽然飞行时间逐渐增加，但总的耗油量在不断降低，油耗与飞行时间成反比关系，由此也可推断随着飞行时间的增加，单位时间的耗油量也在不断减少。

图3 不同飞行时间下校准空速剖面图Fig.3 Calibrated air speed profile under different flight durations

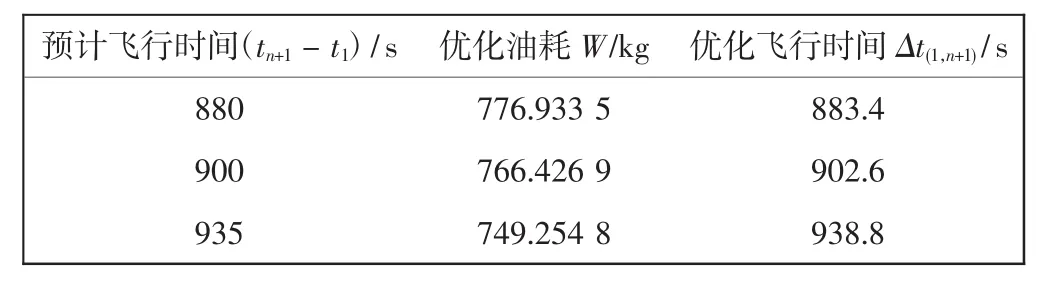
表2 不同预计飞行时间下的性能参数优化Tab.2 Performance parameter optimization under different flight durations

图4和表3为预计飞行时间900s，风速Vw=-10m/s、Vw=0、Vw=10 m/s,利用改进遗传算法进行优化的校准空速随航程距离变化剖面图及优化性能参数表。

图4 不同风速条件下校准空速剖面图Fig.4 Calibrated air speed profile under different wind speeds

表3 不同风速条件下的性能参数优化Tab.3 Performance parameter optimization under different wind speeds

由图4可看出，同一航程在不同风速条件下对应的校准空速并不一致，逆风情况下校准空速最高，无风次之，顺风最低。从表3可发现，顺逆风严重影响航空器的优化油耗，逆风情况下耗油最多，无风次之，顺风最少，即在逆风飞行的情况下，若要在规定时间到达目标航路点，需要消耗更多燃油。因此，航空公司可充分利用气象部门发布的风速、风向信息降低燃油消耗，减少运营成本。

4 结语

以航空器实时下传的ADS-B数据和BADA性能数据库提供的相关性能参数为依据，建立有风状况下飞行剖面的优化策略，并调用遗传算法对航空器在巡航段的剖面进行优化仿真。虽然全程加速的速度剖面与航空器实际飞行有一定误差，但提供了一种新型的剖面优化方法，其结果也可为管制自动化系统自动化管制飞行剖面提供部分参考意见。结论如下：①基于爬山算法的改进遗传算法能大大减少优化时间，提高算法收敛速度；②高空风速的大小、方位对于剖面优化有重要影响，故从提高剖面优化精度考虑，不能忽略。

实际飞行过程中，处在巡航阶段的航空器在偏离了正常的巡航速度后，需尽快回归正常巡航速度。下一步的研究方向是优化数学模型，更加契合实际。