微小卫星临近操作仅测距初始相对定轨解析方法

施俊杰，龚柏春，李 爽，白艳萍，李 欣

(1. 南京航空航天大学，南京210016；2. 中科院微小卫星创新研究院，上海201203； 3. 中国人民解放军92728部队，上海 200436)

0 引 言

随着近年来微小卫星技术的蓬勃发展，基于微小卫星平台的空间在轨服务趋势已经出现[1]，例如已经进行过在轨试验的美国XSS-11系统。而微小卫星因为其平台的特殊性，在能源、载荷等多方面都受到限制。例如，微小卫星难以支撑体积大、功耗高、系统复杂的微波雷达等常用的交会对接传感器。而常用的光学交会相机也会受到复杂空间环境的种种限制，特别是太阳光照对相机的影响非常大，存在使用窗口问题。因此，光学交会相机的使用窗口限制了微小卫星面向在轨服务交会对接的时间自由度，从而需要有基于其他传感器的定轨方式作为有效补充，也就引出本文研究的仅测距定轨问题。

仅测距定轨，即在仅有相对距离测量信息的情况下实现轨道确定[2]。通过无线电通讯测距，不需要增加其他载荷、对空间环境不敏感，不增加能源消耗，仅测距定轨的方式具有其独特的优势。与研究较多的光学相机仅测角定轨一样，仅测距定轨属于测量信息不完备情况下的导航问题。仅测距定轨的概念和应用最早出现于二十世纪六十年代，工程师们采用单个地面测控站测量与卫星的距离，以多组测量实现卫星的定轨[3]。之后，仅测距定轨也被应用在天基卫星对同步轨道卫星的监测定轨任务之中[4]。近年来，随着航天器在轨服务和编队飞行概念的发展，部分学者已经开始着眼于航天器相对运动研究仅测距定轨问题[5]。由于仅测距定轨缺乏视线角信息，使得在相对运动轨道动力学环境下利用距离信息进行定轨时存在轨道模糊性的镜像解问题，即同一组距离信息不能唯一确定真实的相对轨道。Chavez、Doolittle、Lovell和Rundberg等人从相对轨道要素验证了仅测距定轨的模糊性问题[6-8]。Maessen和Gill基于相对轨道要素讨论了双星编队仅测距相对导航的状态可观测性问题，给出了先验信息较差时系统也不能输出正确相对轨道的结论[9]。Wang和Butcher在Tschauner-Hempel动力学下研究了椭圆目标轨道的仅测距相对导航问题，得出了目标轨道的非零偏心率可以排除“退化”的镜像轨道，但保形镜像轨道依然存在的结论[10]。Christian在Clohessy-Wiltshire(C-W)动力学下研究了仅测距初始定轨与实时导航问题，提出了采用轨道机动去模糊从而实现仅测距导航的方法[11]。然而，在未知相对轨道的情况下进行轨道机动给交会对接带来了潜在碰撞风险以及额外的燃料消耗。

现有的仅测距方法研究中，都是在假定测距传感器在航天器质心安装的基础上进行推导的。然而，在实际工程中很难将测距传感器在航天器质心安装，进而质心安装的假定具有一定的局限性，即只能在远距离交会时近似成立，在近距离交会时这种假定会带来定轨不确定性，即出现杆臂效应问题。而本文正是利用杆臂效应解决仅测距相对定轨的模糊性问题，实现将带来不确定性的因素转化为确定状态的充分条件。文章首先给出采用的坐标系定义和相对运动动力学模型，对仅测距相对定轨解的模糊性问题进行分析；然后详细推导基于传感器偏置杆臂效应的仅测距相对定轨算法；最后通过数值仿真验证所提算法的有效性，并分析定轨性能。

1 相对运动动力学模型

首先以右手准则建立第二轨道坐标系LVLH。航天器A的质心为原点，定义地心指向航天器A质心的方向为x轴，轨道面内垂直于x轴指向A的速度方向为y轴，z轴满足右手定则。

在近地近圆轨道、两航天器之间的距离远小于轨道半径且不考虑相关摄动的的假设前提下，航天器A与B之间的轨道相对运动可以由Clohessy-Wiltshire方程进行建模[12-13]，其状态转移模型如下[14]

(1)

(2)

(3)

(4)

(5)

式中，ω是航天器A的轨道角速率，不失一般性情况下假设近圆轨道的ω为定值。

2 仅测距定轨的模糊性分析

在航天器相对运动应用中，相对距离信息的测量可以通过激光测距仪、无线电通信TOA等方式完成。假设测距传感器(激光或无线电接收端)在LVLH坐标系下的位置为ra=[xa,ya,za]T，并且该传感器与航天器A相固联。该传感器可以测得任意时刻与航天器B的相对距离ρ(t)，如图1所示。

根据三角几何关系可以得到

(6)

由式(2)～(5)，可知轨道面内的相对运动与轨道面外的相对运动之间独立。所以令

(7)

(8)

(9)

(10)

(11)

于是式(6)可以改写为

(12)

其中

(13)

(14)

定义矩阵Mxy为4×4矩阵

(15)

定义矩阵Nz为2×2矩阵

(16)

于是式(14)改写为

(17)

当za=0，有

(18)

根据式(16)与(18)可得：矩阵Nz是一个对称的半正定矩阵，并且矩阵的秩为2。所以，如果γ0是定轨的一个解，那么(-γ0)必定也是定轨的一个解，并且这两个解在任意时刻均会产生相同的测距结果，即

(19)

因此，若za=0，那么定轨的解，即航天器B的初始状态必然呈现多解。同样地，由式(13)可以得到：若xa=0且ya=0，那么定轨必然也会呈现模糊性。文献[11]当中所论证的多解情况，是xa、ya、za全部为零的特殊情况，即收发信号的传感器位于航天器A的质心。

此外，当测距传感器在LVLH系中的方位时刻指向航天器B，则有

ra=kx

(20)

(21)

此时根据文献[11]，可知该情况仍存在模糊性问题。然而在实际飞行过程中，测距传感器很难一直精确指向目标航天器的质心，所以本文后续的讨论中将假设这种情况不存在。

因此，仅测距的初始相对定轨解不存在模糊性的必要条件是“za≠0且xa与ya不全为零”。

3 基于杆臂效应的仅测距解析定轨算法

将式(1)代入式(6)中，得到

Esinωt+Fcosωt+Gsin2ωt+Hcos2ωt+I

(22)

其中，系数A～I分别为

(23)

(24)

(25)

(26)

(27)

(28)

(29)

(30)

(31)

由于等式(22)右侧，9个关于时间t的基函数线性无关，故系数A～I为定值。式(23)～(26)可改写为

(32)

(33)

(34)

(35)

由式(32)可得

(36)

将式(36)代入式(35)，可以得到

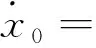
(37)

将式(36)代入式(34)，可以得到

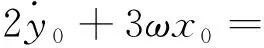
(38)

由(36)与(38)式，可以得到

(39)

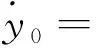
(40)

再由(33)可得

(41)

将式(37)～(41)分别代入至式(27)和式(28)中，有

(42)

(43)

至此得到了航天器B的初始状态x(0)

(44)

由式(44)可知，初始轨道状态x(0)存在两组解。下面通过式(28)～(31)排除其中的镜像解，由此避免解的模糊性。

分别将式(44)当中的两组解代入式(29)当中，如果其中一组解满足该式，而另一组解不满足，就可以排除多解，得到初始状态的真实解的情况。假设式(44)当中的真实解为1x(0)，另一组解(多解)为2x(0)，那么当

(45)

时就能排除多解。将式(44)代入式(45)得

(46)

再将式(23)～(31)代入式(46)得

(47)

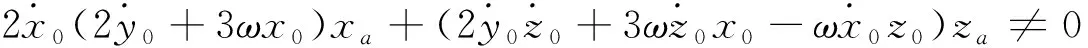
还可以依据其他系数来排除多解。由式(28)、(30)与(31)得

2(x0xa+y0ya+z0za)]

(48)

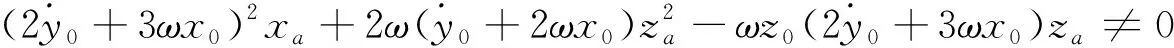
综合上述分析方法，可以得出以下结论：当航天器B相对于航天器A的轨道为非周期轨道时，如果收发信号的传感器在LVLH系当中的位置满足以下条件：

①xa≠0且za≠0；

②xa与za不是以下方程组的解；

时，就可以根据式(28)～(31)排除式(44)当中的一组解，进而得到航天器B相对于A的初始状态。

再根据式(1)即可利用C-W方程得到任意时刻航天器B相对于航天器A的位置，实现相对定轨。

4 数值实例

为了验证所提算法的有效性，并分析安装和测距等不确定性带来的定轨误差，本文进行了两组仿真：1.无误差条件下仿真有效性验证；2. 不确定条件下仿真定轨误差分析。

4.1 无误差仿真

4.1.1参数设置

4.1.2仿真结果与分析

首先需要在不同的时刻对航天器B到传感器的相对距离进行9次测量，根据式(22)求解出9个系数A～I；此后利用式(44)求解出两组不同的初始状态；最后通过式(28)～(31)排除多解，得到航天器B的初始状态。

为了避免求解系数A～I时出现奇异，测距的时间间隔不能为(T/4)及其整数倍，同时测距时间间隔也不能过短。

相对轨道为跳跃轨道和共椭圆轨道的仿真结果见表2所示。

对比仿真结果与初始位置的真值可以发现，对于跳跃轨道与共椭圆轨道这两种非周期轨道，该算法的结果与理论值符合较好。

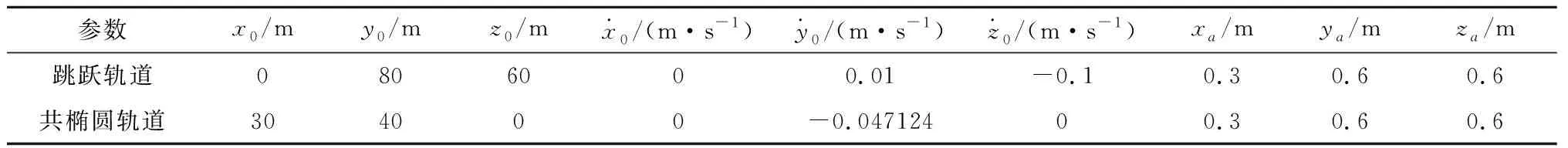
表1 仿真参数设置Table 1 Simulation parameters setting

表2 无误差仿真结果Table 2 Simulation results for error-free cases

4.2 不确定条件下的定轨仿真

4.2.1参数设置

采用与4.1.1节中相同的初始轨道等参数。此外，假设在组装航天器A时，传感器的位置存在1%的常值安装误差，即Δra=(0.003,0.006,0.006)T；假设传感器测距时，存在测距常值偏差Δρ和服从正态分布的测距随机偏差ΔρN。它们满足

Δρ=0.01, ΔρN～N(0,0.012)

其中，速度单位均为m/s，长度单位均为m。

4.2.2仿真结果与分析

为了使相对定轨结果更加准确，假定在每一次定轨过程中均测量100次相对距离的值，其中相邻两次测量的时间间隔为100秒。利用这100次测距结果，通过最小二乘的方法，得到系数A～I较为精确的值。进行2000次Monte Carlo打靶仿真，图2和图3分别表示了相对轨道为跳跃轨道时，航天器B的6个初始轨道参数的带误差仿真计算值与理论

参考值的分布关系。图4和图5展示了共椭圆轨道时的仿真结果。对仿真结果进行统计分析，得到了如表3与表4所示的定轨误差均值以及误差方差。

从表3和表4可知，不确定条件下x方向与y方向的定轨精度较高，而z方向定轨不确定性较大，这是因为定轨解中只有z方向的分母中包含偏置量za，za的误差经过倒数后会放大定轨误差，za越小其误差放大效果越突出。同时，对比跳跃轨道与共椭圆轨道的仿真结果可知，对前者的定轨精度要远高于后者，主要因为共椭圆轨道时两航天器间的相对距离先减小后增大，有限的传感器偏置能够提供的可观测度随着相对距离的增大而快速下降。

E(δx0)/mE(δy0)/mE(δz0)/mE(x0)/(m·s-1)E(y0)/(m·s-1)E(z0)/(m·s-1)跳跃轨道-8.815886×10-46.189603×10-3-7.00129510-17.731142×10-72.001996×10-66.511063×10-4共椭圆轨道9.043480×10-41.652821×10-3-3.954493×10-2-1.413811×10-7-1.714118×10-64.942361×10-4

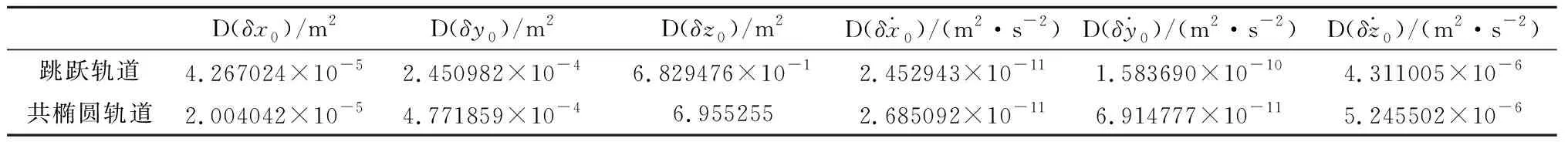
表4 初始定轨三轴误差方差Table 4 Three axes initial orbit determination error deviation

5 结 论

本文首先在C-W相对运动动力学模型的基础上，分析了仅测距相对定轨当中存在的模糊性问题。然后基于测距传感器偏离航天器质心安装的杆臂效应，提出一种解析的仅测距初始相对定轨算法，并给出了测距传感器的安装准则。最后对所提算法进行了无误差条件下与不确定条件下的仿真验证，并分析了安装和测距等不确定性带来的定轨误差。仿真结果表明，该算法具有较高的精度与可靠性。