旋转非合作目标相对状态的解耦估计方法
2018-09-07李宜鹏解永春
李宜鹏,解永春,2,3
(1. 北京控制工程研究所,北京100190;2. 空间智能控制技术重点实验室,北京100094; 3. 天津市微低重力环境模拟技术重点实验室,天津300301)
0 引 言
为了能够安全实施在轨维修、燃料加注等一系列在轨服务,在近距离接近空间目标时需要估计相对位置和姿态(相对位姿),对于安装有合作标志器的合作目标和未安装合作标志器但模型已知的非合作目标,该问题已经得到了很好的解决。而空间目标大多数为模型未知的非合作目标(例如失效卫星、空间垃圾等),未安装合作标志器且缺乏关于几何结构和惯量参数的先验知识,这就给此类目标接近操作过程中的相对位姿估计带来了很大的困难,通常无法直接获取目标本体坐标系的相对位姿。对于无旋转运动或绕单轴旋转的目标,其惯量参数及质心位置是不完全可观的;只有处于章动状态时,目标的惯量参数及质心位置才是可观的[1-2]。因此本文以模型未知且处于章动运动的非合作目标为研究对象,研究接近过程中目标质心位置、惯量主轴、线速度、角速度及转动惯量比等相对状态的估计方法。
未知非合作目标的相对状态估计问题可以用典型的同时定位与建图(Simultaneously localization and mapping,SLAM)问题来描述[2-5],即在恢复目标三维结构的同时,对目标的相对位姿进行估计,对于旋转运动的目标,还需要估计质心、惯量主轴等相对状态。对此国内外学者主要采用视觉敏感器作为测量手段,并设计相应的估计方法对目标的相对状态进行估计。根据原理的不同,文献中的方法主要分为三类:基于运动学的方法、建立辅助坐标系的方法和直接估计的方法。
基于运动学的方法[1,6-10]一般使用双目相机或激光雷达获取目标特征点的位置以及相邻时刻目标位姿的变化量,通过差分运算近似得到目标的角速度以及特征点的线速度,并以此作为测量值,根据目标的角动量守恒方程和特征点的旋转-平移耦合运动方程,使用最小二乘法分别估计出目标的惯量参数、质心位置及速度。这种方法的主要缺点是差分运算引入的噪声对估计结果影响较大。
建立辅助坐标系的方法的基本原理是通过人为定义一个固定于目标上的坐标系,以该坐标系的相对位姿作为观测量,再根据目标的动力学模型估计目标的惯量参数[2,11-12]。在建立目标的动力学模型时,需要将未知的转动惯量比、辅助坐标系与目标本体系之间的偏移量做为待估计状态变量,通过UKF[11]、EKF[12]或者增量平滑与建图(incremental Smoothing and mapping,iSAM)[13]进行估计。此类方法的优点是能够更精确地估计目标的线速度、角速度等状态,缺点是建立辅助坐标系导致待估计变量的数量增加。
直接估计的方法是以目标表面特征点的投影作为观测量,不需要显式地估计出目标的相对姿态和位置,通过建立特征点运动模型及非合作目标的动力学模型,设计滤波算法对目标的相对状态进行估计。比如文献[14-15]使用单目相机观测到的特征点单位视线方向作为观测量,通过追踪航天器的轨道机动、姿态机动或相机安装位置偏置来保证特征点距离的可观性,再通过滤波算法估计出目标的相对状态;特征点深度值的可观性问题可以通过使用双目相机来克服,不需要额外的轨道或姿态机动就可实现,文献[16]使用双目相机对目标进行测量,针对惯量矩阵不确定的问题,设计了多个IEKF滤波器,通过最大后验概率的准则选取最优的估计值;文献[17]在文献[16]的基础上增加了特征点的深度信息和光流作为额外的观测量,并使用文献[2]中的方法对转动惯量进行参数化。
直接估计的方法兼顾了前两种方法的缺点,但是相关文献中所提出方法存在的问题是目标特征点与目标质心之间的相对位置无法确定(无论是在目标本体系下还是在追踪器本体系下都如此),在滤波初始化时很难给出准确的初始值及协方差矩阵,因此会造成滤波算法性能的降低。针对这一问题,本文以双目相机对目标特征点的投影作为观测量,定义不同目标特征点位置的差值为相对特征,通过分析发现相对特征的运动只与相对旋转运动有关,而与相对平移运动无关,且通过双目相机可以直接测量相对特征在追踪器本体系下的表示,在此基础上进一步分析了相对特征的投影模型,以相对特征作为观测量,根据非合作目标的旋转动力学模型对目标惯量主轴、惯量比、角速度进行估计。以目标特征点的位置作为观测量,结合目标本体坐标系相对姿态的估计值,通过相对平移动力学模型对目标的质心位置、线速度进行估计。最后,通过数值仿真校验所提出解耦估计方法的有效性。
1 运动模型
1.1 坐标系定义

1.2 动力学模型
非合作目标本体系相对于追踪器本体系的相对姿态用四元数qct表示,在此分别引入两种四元数乘法算子为[18]:
(1)
式中:q=[Tη]T,为四元数的向量部分,η为四元数的标量部分,I为单位矩阵,[a]×为向量a=[a1,a2,a3]T的反对称矩阵,即
(2)
与四元数q相对应的旋转矩阵为:
C(q)=(2η2-1)I+2T+2η[]×
(3)

ωr=ωt-CT(qct)ωc
(4)
相对旋转的运动学方程为:
(5)
(6)
非合作目标与追踪器之间的相对旋转动力学模型可以由下式描述:
(7)
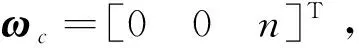

(8)

(9)
1.3 相对特征运动模型
首先建立非合作目标表面特征点的运动模型,假设有N个表示在非合作目标本体系下的特征点,记为fi(i=1,…,N),特征点固定在非合作目标上,即满足
(10)
则特征点fi在追踪器本体系下的观测向量ri为:
ri=rct+C(qct)fi
(11)
对式(11)求一价导数可得:
(12)
由式(12)可以看出非合作目标上固定特征点在追踪器下的观测向量受旋转和平移运动的耦合影响。直接以ri=[xiyizi]T在双目相机像平面的投影作为观测向量进行滤波运算的难点是fi在非合作目标本体系下的坐标无法得知,因此很难选取合适的初始值及初始协方差矩阵,这也是文献[16-17]中仿真结果出现估计偏差的原因。
为解决这一问题,本文提出相对特征的概念,将相对旋转运动估计和相对平移运动估计进行解耦。考虑非合作目标表面上两个不同的特征点fi和fj(j≠i),则相对特征的定义为:

(13)
则相对特征在追踪器本体系下的观测量为:

(14)
则相对特征在追踪器本体系下的一阶导数为:
(15)

2 观测模型
如图2所示,假设在追踪器上安装有固定的双目相机,两相机的光轴平行,两相机的焦距均为f,两相机之间的基线长度记为b,两相机的像主点分别为[luclvc]T和[rucrvc]T,以左相机的坐标系作为双目相机的参考系,为简单起见,假设左相机的坐标系与追踪器的本体坐标系重合。
非合作目标上的特征点fi在左右相机上的投影分别为
(16)
其中,b=[b0 0]T,π(·)为相机投影函数:
(17)
其中a=[a1a2a3]T。

(18)

(19)
对式(19)进一步变换可得相对特征横坐标的计算方程:
(20)
使用双目相机求特征点深度信息的函数为:
式中:f为相机焦距,b为左右相机之间的基线长度,du=lu-ru为特征点在左右相机像平面投影横坐标的差值,将上式代入式(20)可得:
(21)
同样,可以得到相对纵坐标的计算方程为:
(22)
同理可以得到相对特征在右相机像平面的虚拟投影,经过验证相对特征在左右相机的虚拟投影是相等的,因此仅将相对特征在左相机的投影作为观测量即可,值得注意的是,在构造相对特征时需要首先计算特征点的三维坐标,并对相对特征进行初始化,相对特征的虚拟投影可以直接根据式(21)和式(22)计算得出。为避免出现奇异,所选择特征点的深度值不能太接近。
3 相对状态估计
第1节和第2节分别描述了非合作目标与追踪器之间相对运动的动力学模型和使用双目相机作为测量设备时的观测模型,并在此基础上提出了相对特征的概念,用于对非合作目标相对旋转估计和相对平移估计进行解耦。本节主要描述使用相对特征对非合作目标相对旋转运动进行估计的方法以及使用特征点位置对相对平移运动进行估计的方法。
3.1 相对旋转运动估计
非合作目标相对旋转运动系统的待估计参数包括惯量主轴的姿态四元数、角速度、转动惯量比以及相对特征在左相机坐标系下的三维坐标表示。由于非合作目标的惯量参数未知,需要对转动惯量进行参数化,并将其作为待估计变量,另外直接使用加性姿态四元数进行滤波有一定的局限性,因此本文使用乘性误差四元数作为状态变量进行估计。
3.1.1转动惯量参数化
由于非合作目标的惯量参数未知,进行状态估计时无法直接使用式(7),需要对转动惯量比进行参数化,文献[2,10,11,15]分别使用了几种不同的方法对转动惯量比进行参数化,但参数化后的惯量比取值范围还有一定的约束,因此本文提出一种新的参数化方法使惯量比为相互独立的变量,非合作目标的姿态动力学方程为:
(23)
由于非合作目标本体系原点在质心上,且坐标轴与惯量主轴平行,因此转动惯量矩阵Jt为对角矩阵,记Jt=diag(J1,J2,J3),假设非合作目标的转动惯量矩阵满足J1 (24) 式中: (25) 现对式(25)中的惯量比做如下变换: (26) 式中:ea=exp(a), -∞ 将式(25)中的惯量参数代入式(24)可得: (27) (28) 3.1.2乘性误差四元数 直接使用四元数进行状态估计有一定的局限性,首先是参数的自由度,描述姿态的参数自由度为3,而四元数有4个变量;其次四元数有范数为1的约束条件。因此,在使用四元数描述姿态时,通常使用乘性误差四元数设计估计算法,记非合作目标本体坐标系姿态四元数的误差为: (29) (30) 3.1.3滤波算法 定义该系统的状态向量为: 其中,1≤s≤S,此处为了描述方便,假设有S个相对特征,xr对应的动力学模型可以用下式来描述: (31) 其中,xr中相应状态变量的动力学方程在第1节中给出,Gr=diag(03×3,Gω,03S×3S),相对旋转运动估计时以相对特征作为观测量,即 (32) 对过程模型的线性化如下: (33) 其中,M和N可以从式(27)分别对角速度和转动惯量比求导得出。 测量模型的Jacobian矩阵可以通过对式(32)求一阶导数得到: (34) 其中, 最后使用标准的扩展卡尔曼滤波器对式(33)和式(34)所表示的过程模型和测量模型进行状态估计。注意由于使用了乘性误差四元数来描述目标旋转动力学,因此姿态四元数的更新使用四元数乘法实现。 由于非合作目标表面特征点的运动受旋转耦合影响,根据所建立目标质心、特征点运动方程以及所估计的旋转运动量针对质心及其速度设计估计算法, 以特征点的位置作为观测量 (35) 对应的过程模型为: 式中:G0=diag(03×3,I3×3,03N×3N),第i个特征点的观测量构成的观测方程为: yt,i=[I0…C(qct)…]xt+νf (36) 式(35)和式(36)所表示的非合作目标质心过程模型和测量模型均为线性函数,因此使用标准的线性卡尔曼滤波器即可估计出目标的相对平移运动,此处不再赘述。 为了校验本文所提出方法的有效性,本节通过非合作目标相对运动的动力学模型模拟相对运动轨迹,并根据相对运动轨迹及双目相机成像模型产生特征点在图像上的位置,最后根据双目相机的模拟观测信息。为了说明本文方法的优点,分别使用本文所提出方法和文献[16]中的方法对非合作目标的相对状态进行估计,并对仿真结果进行对比分析。 追踪器的轨道近似为圆轨道,其半径设置为7170 km,由此可以计算出轨道真近点角速率n=0.0001 rad·s-1,追踪器的转动惯量矩阵Jc=diag(500,600,700) kg·m2,非合作目标的转动惯量矩阵Jt=diag(410,578,751) kg·m2。左右相机的焦距均为f=8 mm,像元尺寸为5.5 μm×5.5 μm,图像分辨率为2048×2048,两相机的像主点均为[1024 1024],相机的之间的基线长度b=0.3 m。固定在非合作目标上的特征点分布如表1所示。 表1 特征点位置分布Table 1 The distribution of feature points’ position 动力学仿真时间为0~200 s,步长为0.1 s,仿真初始条件设置如下: 为了方便对比本文方法和文献[16]方法对旋转非合作目标姿态角度的估计值,将姿态四元数转换为轴角的形式。由于文献[16]没有直接对目标转动惯量比进行估计,因此仅给出本文方法对转动惯量比的估计曲线。 图3~5分别为非合作目标惯量主轴姿态四元数、角速度和转动惯量比估计值与仿真所使用真实值之间的误差随时间的变化曲线。图3中,本文方法所估计的姿态四元数转换成轴角后的角度误差范围为[-1,1]°,图4中本文方法所估计的角速度误差范围为[-0.3,0.3](°)·s-1,所估计的转动惯量比误差范围为[-0.02,0.02],说明本文所设计的相对旋转运动估计方法能够有效地对非合作目标的惯量主轴、角速度及转动惯量比进行估计。 图6、图7分别为非合作目标质心相对位置和速度与真实值的误差随时间的变化曲线。本文方法所估计的质心位置的估计误差范围为[-0.02, 0.02] m,质心速度的估计误差范围为[-0.001, 0.001] m·s-1,充分说明相对平移运动估计算法的有效性,值得注意的是,对相对平移运动进行估计的时候,需要将非合作目标惯量主轴姿态四元数的估计值作为输入,由此也进一步验证了相对旋转运动估计结果的有效性。 仿真结果表明,文献[16]方法估计结果出现偏差,主要原因是非合作目标特征点与目标质心的相对位置是未知的,因此初始化滤波器初始状态时很难选取合适的初始值及初始协方差矩阵,导致滤波器的性能降低。本文所提方法使用相对特征实现了旋转运动和平移运动估计的解耦,解决了状态初始值不确定的问题,从而提高了滤波器的性能。 针对在轨旋转非合作目标相对状态估计中的特征点位置不确定的问题,本文提出了一种使用相对特征对相对旋转和相对平移运动估计进行解耦的方法。通过建立相对特征运动模型及使用特征点计算相对特征投影的观测方程,设计扩展卡尔曼滤波器对目标惯量主轴、角速度及转动惯量比进行估计;根据特征点的耦合运动模型设计卡尔曼滤波器对目标质心及速度进行估计。通过仿真的对比分析,证明本文所提出的解耦估计方法能够有效地对旋转非合作目标的相对状态进行估计。 本文所提出的使用相对特征进行解耦估计的方法需要通过双目相机进行测量才能实现,考虑到通过安装位置偏置的单目相机也可以保证特征点深度信息可观[14-15],因此未来考虑研究基于单目相机的解耦估计方法。
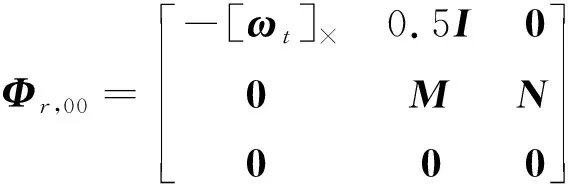
3.2 相对平移运动估计

4 仿真分析
4.1 仿真条件

4.2 仿真结果分析
5 结 论
