考虑根铰间隙的空间框架展开机构动力学分析
2018-09-07杨淑利刘志全濮海玲杨巧龙
杨淑利,刘志全,濮海玲,杨巧龙
(中国空间技术研究院总体部,北京 100094)
0 引 言
空间柔性太阳电池阵一般采用盘压杆、铰接杆或管状杆展开机构实现其展开或收拢运动,而多模块框架的柔性太阳电池阵新型展开机构因具有质量轻、刚度高、收拢体积小、模块数量可灵活调整等优点[1-2],更受航天界的青睐。
然而多模块框架展开机构的根铰间隙对展开机构的自由度数目、拓扑结构和动力学特性存在显著影响[3],使运动部件动应力增加,引起部件的振动与冲击,导致运动精度下降[3-4]。因此,进行考虑根铰间隙的空间框架展开机构动力学分析具有重要意义。
2003年,美国空军研究室的A. L. Adler等对多模块框架展开机构进行了初步动力学分析,分析了在重力作用、不同边界条件下的基频和模态,指出铰链间隙对框架展开过程有一定影响,但并未进行影响分析[6]。2004年,中国空间技术研究院王巍针对国内空间太阳电池阵常用无源驱动扭簧式铰链进行了间隙铰链分析模型研究,将铰链间的接触力假设为单向的非线性弹簧,得到包含间隙影响的铰链力矩-转角关系曲线[5],但只进行了单自由度展开机构的动力学分析,未涉及多自由度展开机构的动力学分析。2005年,美国ABLE Engineering研究机构的M. Eskenazi等对不同模块数目和不同展开构型的多模块框架展开机构用有限元方法进行了基频和变形分析[7]。2013年,哈尔滨工业大学张静针对空间含铰可展桁架结构,综合考虑间隙、非线性刚度、摩擦及碰撞阻尼四种因素建立铰链等效模型,并基于此模型开展非线性动力学建模与分析[8],但文献[8]只针对展开后的桁架结构在定点外部激励下研究桁架结构的动力学响应,并未进行展开过程中的桁架动力学分析。总之,文献[5]~[8]均未进行框架展开机构展开过程的动力学分析,也未考虑有源驱动下铰链间隙对多自由度框架展开过程动力学特性的影响分析。
针对上述问题,本文利用Kane方法建立考虑根铰间隙的多模块框架展开机构多体系统动力学模型,对多模块框架展开机构在三维空间展开过程中各组件及节点的动力学特性和根铰间隙的影响进行仿真分析,以期获得多模块框架展开机构的运动学参数、动力学特性和根铰间隙的影响规律,为该类多模块框架展开机构设计提供依据。
1 多模块框架展开机构的组成及展开过程
多模块框架展开机构是由若干个支撑梁和铰接单元组成。展开后形成模块化、大面积的展开结构;随后柔性毯在每个矩形模块内展开(见图1)。每个标准模块内的太阳电池阵的展开方式都是相同的,可以根据需要进行扩充或减少标准模块数量,也可以设计不同的布局对模块进行拓展,以满足不同航天器的各种功率需求。
图2为单模块框架展开机构完全展开后的状态。单模块电池阵的主要承力单元为4根侧梁、1根基梁和1根端梁,展开后构成一个矩形。各梁之间由铰接单元连接,铰接单元分为动力铰接单元、从动铰接单元及中间铰接单元。根部动力铰接单元由电机-减速器轮系提供框架展开动力,从动铰接单元没有动力铰接单元的电机-减速组,但含有锁定-缓冲机构,以实现展开后锁定。2根侧梁中间的节点称为中间铰接单元,不含电机-减速组,只起到连接和展开侧梁的作用,并实现展开后锁定。
以下就双模块框架展开机构的展开过程做简要描述,如图3所示。对于双模块框架展开机构,共有9个铰接节点,其中:①为根部动力铰接节点,③④⑥⑦⑨为从动铰接节点,②⑤⑧为中间铰接节点。在展开过程中,①点为根部固定点,由电机提供展开动力,使得①②梁与①⑥梁各自实现90°旋转展开,并通过从动或中间铰接单元带动其它各梁的顺利展开。为了保证各梁在展开的过程中不发生干涉或交叉,且各梁同步展开,需要遵循以下约束条件:
1)由①②、④⑤、⑦⑧分别连接的梁保持平行;
2)由②③、⑤⑥、⑧⑨分别连接的梁保持平行;
3)由①⑥和③④分别连接的梁保持平行;
4)由⑥⑦和④⑨分别连接的梁保持平行。
2 考虑根铰间隙的框架展开机构动力学建模
本文基于Hertz接触理论建立框架展开机构的根铰(旋转铰)间隙力学模型,并利用Kane方法对框架展开机构进行动力学建模。
2.1 根铰间隙力学模型
根链销轴与轴瓦的接触如图4所示。
设销轴与轴瓦的弹性模量、泊松比及半径分别为E1,E2、ν1,ν2、R1,R2。Dubowsky推广了Hertz接触定律[9-10],提出法向接触力FN与变形δ的非线性关系式为
(1)
式(1)中:R、k1和k2分别为
(2)

2.2 基于Kane方法的框架展开机构动力学模型
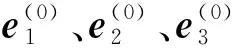
本文根铰间隙包括AB梁绕O1旋转铰和AF梁绕O2旋转铰的间隙。旋转铰示意图如图7所示,图7中O1,O2分别为A点处两个旋转副轴瓦的中心。在图7所示的情况下,外力有惯性力和惯性力矩。为了求得构件惯性力和惯性力矩,要确定各构件质心的位置、速度和加速度与广义坐标的函数关系。设各梁的质心位移和角位移向量分别为Li,θi,(i=1,2,3,4,5,6);各梁质心速度和角速度向量分别为
Vci,ωi,(i=1,2,3,4,5,6);各梁质心加速度和角加速度向量分别为aci,εi,(i=1,2,3,4,5,6)。需要指出的是,为满足第1节中各梁的约束条件,则l1=l6,l2=l5,l3=l4。
a)各构件质心位置、速度、加速度
用向量Li表示质心位置,有
(4)
由式(4)可知,各构件质心速度、角速度及构件质心加速度、角加速度分别如式(5)~(6),并将其转换为对广义坐标及广义速度的表达式。
(5)
(6)
b)框架展开机构的主动力(矩)和惯性力(矩)
由于考虑根铰间隙影响,轴瓦分别对AB梁和AF梁的销轴有摩擦力和接触力的主动力;故系统受到的主动力包括作用在AB梁上的驱动力矩M1,销轴处的接触力FN1与摩擦力FT1;作用在AF梁上的驱动力矩M4,销轴处的接触力FN2与摩擦力FT2。设AB梁A处的旋转铰轴瓦与销轴的半径分别为r1,r2,AF梁A处的旋转铰轴瓦与销轴的半径分别为r3,r4。近似把摩擦力FT1、FT2简化为对刚性杆销轴的力矩MT1和MT2。设连接AB梁的旋转铰接触刚度系数、阻尼系数和摩擦系数分别为K1,D1,μ1,连接AF梁的旋转铰接触刚度系数、阻尼系数和摩擦系数分别为K2,D2,μ2,则有
则主动力、主动力矩为
惯性力、惯性力矩为
c)广义主动力和广义惯性力
将主动力(矩)和惯性力(矩)转移到广义坐标中,即首先求出各构件质心速度与角速度对广义速度的偏微分,构成转换矩阵,然后将其与力向量相乘,即可获得广义力,转换矩阵为
广义主动力为
F=UF[FN1,0,0,FN2,0,0]T+
UM[M1+MT1,0,0,M4+MT2,0,0]T
框架的动力学方程表示为
F+F*=0
由此可得到框架的动力学模型如式(7)~(12)所示
M1+FT1r2=0
(7)
(8)
M4+FT2r4=0
(9)
(10)
(11)
(12)
3 框架展开机构动力学仿真结果分析
根据2.2节框架展开机构动力学模型,运用经典四阶Runge-Kutta法来求数值求解,通过MATLAB进行编程,得到框架展开机构运动学及动力学参数的数值解。且采用2.2节建立模型的方法,也能够求解其它一维或二维框架展开机构的动力学参数。本算例中采用的各输入参数为见表1。算例中x01、y01的初始值分别选取为0、-0.0001 m,y02、z02的初始值分别选取为-0.0001 m、0 m,θ1、θ2的初值均为0°(框架展开机构处于收拢状态)。

表1 框架展开机构动力学仿真参数 Tabble 1 Parameters of deployable strut-mechanism for dynamic analysis
3.1 根部转角随时间变化曲线
图8、图9分别为考虑和不考虑根铰间隙下框架展开机构AB梁转角θ1、AF梁转角θ2的动力学响应曲线。
由图8、图9可知:
(4)当M1=1.0,M4=0.3时,θ1和θ2能够在相同的时间内转动90°,同时转到xoz平面内,此时AB梁和AF梁在同一面内呈90°夹角。
3.2 AB梁根部x01,y01,FN1随时间变化曲线
图10、图11、图12分别为考虑根铰间隙下框架展开机构AB梁根部x01、y01、FN1、B点x方向的动力学响应曲线。
由图10、图11、图12可知:
(1)在θ1转动90°的区间内, |x01| 先趋于增大后减小的趋势,最大值为0.00054 m;|y01|在0.0001 m内变化,当θ1=90°时,y01有略微增大的趋势;
(2)FN1随时间的变化渐渐趋于稳定,稳定后FN1约为0.48 N。
3.3 AF梁根部y02,z02,FN2随时间变化曲线
图13、图14分别为考虑根铰间隙下框架展开机构AB梁根部y02、z02、FN2的动力学响应曲线。
由图13、图14可知:
(1)在θ2转动90°的区间内, |z02| 先趋于增大后减小的趋势,最大值为0.00042 m;|y02|在0.0001 m内变化,当θ2=90°时,y01有略微增大的趋势;
(2)FN2随时间的变化渐渐趋于稳定,稳定后FN2约为0.4 N。
4 结 论
(1)基于Kane法多体动力学基本理论及Hertz接触理论建立了考虑根铰间隙的框架展开机构多体系统动力学模型,得到了框架展开机构多自由度展开过程各组件及节点的动力学参数数值解。该模型更加真实地描述了系统的动力学特性,同时也适用于其它一维或二维框架展开机构的动力学分析;
(2)根铰间隙对框架展开机构基梁的转角和角速度几乎没影响,而对角加速度存在较为明显影响。角加速度幅值在0~2 s内波动明显。故对于存在根铰间隙的展开机构,需在机构展开初期阶段(如0~2 s)施加一定的阻尼来降低间隙冲击对铰链的影响;
(3)框架展开机构侧梁AB在x-y面内展开过程中,与AB梁连接的销轴x向位移绝对值呈先增后减趋势,最大值为初始间隙值的5倍;在y向位移基本呈正弦变化态势。故铰链应选弹性和抗疲劳性能较好的材料,以适应交变的冲击载荷;
(4)考虑根铰间隙后,铰链对侧梁AB(x-y面内)产生的接触力稳定值比对基梁AF(y-z面内)产生的接触力稳定值略大,原于铰链间隙和BC梁的冲击;
(5)框架展开机构根铰驱动力矩大小是影响机构展开时间和间隙冲击的主要因素。因此需根据框架展开机构的模块数量和布局设计出合理的驱动力矩,以保证框架展开机构在规定的展开时间内铰链间隙产生的冲击影响最小。
