分析插值误差和斜率的轨迹优化网格细化方法
2018-09-07赵吉松
赵吉松,尚 腾
(1. 南京航空航天大学航天学院,南京 210016;2. 北京航天自动控制研究所,北京 100854)
0 引 言
轨迹优化对于飞行器设计有着重要意义和工程实际价值。轨迹优化属于最优控制问题,其求解方法主要分为间接法和直接法[1]。间接法借助变分法或者庞特里亚金最大值原理,把泛函优化转化为边值问题求解;直接法通过对控制变量/状态变量进行离散把泛函优化转化为非线性规划(Non-linear programming,NLP)求解。直接法中的配点法由于不需要推导最优性必要条件,并且对优化初值的敏感性较低,容易收敛,近年来得到广泛研究。
如果需要高精度求解轨迹优化问题,直接增加节点数量不是一种较好的方案。因为这样处理会导致计算量显著增加,需要更多的计算资源,并且随着节点数目的增加,算法的收敛性通常变差。这种情况下有必要引入网格细化技术对节点进行局部加密或者调整。目前,国内外研究者在网格细化方面已经做了不少工作[2-17]。对于局部配点法,由于离散格式对于节点分布没有限制,因而局部配点法的节点可以根据需要任意布置。用于局部配点法的网格细化方法主要有离散误差分析法[2]、小波分析法[3-4]、多分辨率技术(MRT)[5-10]、密度函数法(DENMRA)[11]等。对于全局配点法(又称伪谱法),其离散节点是正交多项式的根,在离散区间的分布特点是中间稀两端密,但是一旦节点数目给定,节点的分布情况也随之确定。因此,全局配点法的离散节点不可以随意布置,在网格细化方面没有局部配点法灵活。全局配点法的网格细化方法通常是通过添加结点(段与段之间的连接点称为结点)将问题分段优化,利用结点附近的离散节点较密的特点达到加密网格的效果,比如结点伪谱法[12],hp自适应伪谱法[13-14],ph伪谱法[15],以及最新提出的既能添加节点又能减少节点的自适应网格细化算法[16]。分段优化面临的主要问题是通常很难知道需要分多少段以及在哪分段,若通过优化迭代确定这些信息往往会存在分段过多、采用的离散节点较多等弊端[12-16]。
在众多网格细化算法中,多分辨率技术[5-10]非常有吸引力。该技术分析各个节点处的插值误差,如果某个节点的插值误差较大,则在该节点附近细化网格,否则不进行细化。多分辨率技术原理简单、鲁棒性好,采用的节点较少。但是,文献[9]发现,原始多分辨率技术[5-6]可能会出现细化遗漏或者细化失败的问题。另外,多分辨率技术基于二进网格,其初始网格的节点数必须是2j+1(j为非负整数)。文献[9]通过引入广义二分网格并增加检测算法解决了这些问题,但是给出的细化算法较为复杂并且需要较多的网格迭代次数。文献[10]给出一种改进多分辨率技术(IMRT),细化效率较高,但是仍然需要检测算法才能避免细化遗漏或者失败。文献[5-10]本质上都属于多分辨体系。多分辨率技术发生细化不充分的根本原因是由于这种方法在细化过程中将离散节点分成不同的分辨率层次造成的。此外,这种多层次结构的分析方式没有充分利用现有网格中的信息,通常会添加一些不必要的节点。
本文通过直接分析离散节点的插值误差和斜率提出一种新的网格细化方法,能够以较少的网格迭代次数和节点数目高精度求解轨迹优化问题。
1 轨迹优化问题数学描述
轨迹优化问题本质上属于最优控制问题。以Bolza型最优控制问题为例,可描述为:求解控制变量u(t)∈Rm,使得如下目标函数最小化

(1)
式中:端点项M:Rm×R×Rn×Rm→R,积分项L:Rn×Rm×R→R,x∈Rn,t∈[t0,tf]⊆R。
状态方程为
(2)
端点(边界)条件为
E(x(t0),t0,x(tf),tf)=0
(3)
路径约束为
C(x(t),u(t),t)≤0,t∈[t0,tf]
(4)
式中f:Rn×Rm×R→Rn,E:Rn×R×Rm×R→Re,C:Rn×Rm×R→Rc。方程(1)~(4)描述的问题称为Bolza型最优控制问题。
2 基于Runge-Kutta格式的配点法离散
首先利用积分变换τ= (t-t0)/(tf-t0)将最优控制问题(方程(1)~(4))变换至时间区间τ∈[0, 1]。假设单位区间[0, 1]上的N个离散区间的节点为
G={τi:τi∈[0,1],i=0,1,…,N;τ0=0,
τN=τf=1;τi<τi+1,i=0,1,…,N-1}
(5)
式中:τi称为节点或网格点,τi在[0, 1]上可以均匀分布,也可以非均匀分布。
记xi=x(τi),ui=u(τi), 对于状态方程(2),采用q阶Runge-Kutta(RK)方法的离散格式为
(6)
式中:△t=tf-t0,hi=τi+1-τi,fij=f(xij,uij,τij;t0,tf),xij,uij和τij为中间变量,xij由下式给出
(7)
式中:τij=τi+hiρj,uij=u(τij);ρj,βj,αjl均为已知常数并且满足0≤ρ1≤…≤ρq≤1。当αjl=0 (l≥j)时,方程(6)为显式格式;否则,方程(6)为隐式格式。采用类似的方法,可将目标函数离散化。常用的离散格式包括梯形格式(q=2),Hermite-Simpson格式(q=3),以及经典四阶Runge-Kutta格式(q=4)。
(8)
并且满足如下约束
(9)
Ci=C(xi,ui,τi;t0,tf)≤0
(10)
(11)
E(x0,t0,xf,tf)=0
(12)
式中:

3 网格细化算法
由于状态方程决定了状态变量随控制变量的变化规律,状态变量的非光滑特性通常在控制变量中有所反应(对应于控制变量的剧烈变化甚至不连续),因而本文只对控制变量进行细化。当然,如果有必要,也可以同时对状态变量和控制变量进行细化。对于一组离散节点G={τi:i=0,1,…,N}和相应的离散最优控制变量φ={ui:i=0,1,…,N},网格细化是根据轨迹的非光滑特性在某些区域插入新的离散节点或者删除多余的离散节点,从而能够采用较少的离散节点高精度求解轨迹优化问题。
3.1 节点插入方法
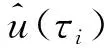
(13)
这种细化方法使得节点τM比τi-1和τi高一个分辨率(步长减半),节点τQ比τM和τi高一个分辨率。这种分辨率层次关系同样适用于节点τM ′和τQ ′。
对于每一个节点进行上述处理,便实现对网格的细化。如果优化问题有多个控制变量,那么在某个节点处只要有任意一个控制变量分量的插值误差超过了预定的误差限,就需要在该节点周围细化网格。与多分辨率技术[5-6]相比,上述节点插入方法具有如下优势。首先,这种方法非常简单、易操作,并且对初始网格的节点数目没有限制。其次,这种方法能够在轨迹的任意插值误差较大的区域持续细化网格,直到满足精度要求或者达到预定的最高分辨率,避免了细化遗漏或者细化失败,也避免了文献[9-10]采用的较为复杂的检测算法。最后,这种方法在计算某个节点的插值误差时从其周围的所有节点中选取最优插值节点,而文献[5-10]只从其周围的同等分辨率节点和更低分辨率节点中选取最优插值节点。可见,本文方法利用了当前网格中的更多信息,因而需要插入的节点数量可能会更少。
3.2 节点删除方法
前述节点插入方法可能会添加一些多余的离散节点,若能够将其删除,显然有利于减小优化计算量。本文只删除左右斜率都为零的节点。以图 1(a)所示的节点τi为例,其左、右斜率分别定义为
(14)
由于上述节点删除方法只能删除左右斜率均为零的节点,而实际上多余节点的斜率不一定为零,因而上述方法是一种比较保守的方法。未来研究中可以设计更加高效的节点删除方法。
3.3 网格细化算法
基于前述节点插入算法和节点删除算法,可设计出轨迹优化网格细化算法。在进行网格细化之前,需要选取初始离散区间数目N,网格细化误差限ε,最高分辨率Jmax,最大迭代次数Imax(Imax≥Jmax/2+1)。采用RK离散方法将轨迹优化问题转化NLP。设置I= 1,Gold=G0,提供NLP优化变量的初值并记为Xold。其中G0为区间[0, 1]上均匀分布的N+1个离散节点。那么,网格细化算法流程如下:
1)在网格Gold上以Xold为初值求解NLP。若I≥Imax,那么结束细化;否则转入下一步。
2)节点插入算法。
3)节点删除算法。
4)本次细化得到的非均匀网格Gnew=Gint,相应的函数值Φnew=Φint。
5)如果细化后的新网格Gnew与旧网格Gold相同,那么结束细化;否则,置I=I+1,将步骤1)解出的NLP最优解插值到Gnew,此作为新的初值Xold,令Gold=Gnew,返回步骤1),继续细化。
在上述网格细化技术的流程中,节点插入算法和节点删除算法是关键,下文分别给出。
节点插入算法:
1)令Φold={uk:τk∈Gold,k=1,…,Nold},将其改写为Φold={φl(τk):l=1,…,m,τk∈Gold}。
2)初始化网格Gint=Gold以及函数值Φint=Φold。
3)设置i=2,执行如下步骤3(a)~3(c)。
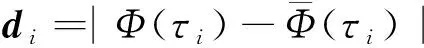
(c)将i增加1。若i≤Nold-1,返回步骤3(a);否则转入下一步。
4)设置i= 3,执行如下步骤(4(a)和4(b))。
(a)若节点τi-1∈Gold和τi+1∈Gold的周围都已经进行了细化,那么在节点τi周围进行补充细化,即将以下节点添加到Gint中
其中,τl和τr分别为节点τi∈Gold在Gint中的左侧相邻节点和右侧相邻节点。
(b)将i增加1。若i≤Nold-2,返回步骤4(a);否则转入下一步。
5)网格Gint为节点插入算法得到的新网格,相应的函数值为Φint。若新增节点的函数值未知,则利用Gold和Φold通过p阶ENO插值计算。
节点删除算法:
1)找出Gint中达到当前最高分辨率的节点,即距离小于1/(22IN)的相邻节点,记为Gmin。
2)用Gcheck表示属于Gint但是不属于G0也不属于Gmin的节点的集合,即
Gcheck={τki:τki∈Gint(Gbase∪Gmin),i=1,…,Ncheck}
集合Gcheck表示需要分析是否可以删除的节点。
3)设置i= 1,执行如下步骤3(a)~3(c)。
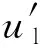
(c)将i增加1。若i≤Ncheck,返回步骤3(a);否则,结束节点删除算法。
4 优化算例
本节应用第3节描述的网格细化方法求解优化算例以验证其有效性和特色,包括Bryson-Denham问题[6]、月球着落问题[13]和航天器姿态调整问题[18]。对于每个算例,采用Hermite-Simpson格式将其转化为NLP,采用SNOPT 7[19]求解,采用INTLAB 5.5[20]提供一阶偏导数。计算平台为MacBook Air(处理器Intel Core i5-5250U 1.6 GHz,操作系统Windows 10企业版,编程语言MATLAB R2009a)。算例中的优化耗时为10次运行的平均值。另外,在每个算例中都给出了其它方法的优化结果作为对比。
4.1 算例1:Bryson-Denham问题
Bryson-Denham问题[5]又称最小能量控制问题,是非光滑轨迹优化的常用算例。该问题具有解析最优解,能够检验本文方法的精度。该问题描述为求解最优控制u(t),使得如下目标函数最小
(15)
并且满足动力学方程
(16)
初始条件x(0) = 0,v(0) = 1;终端条件x(1) = 0,v(1) = 1;以及路径约束(状态变量边界约束)
x(t)≤l
(17)
式中:l为实数,本算例取l= 0.04。
采用本文的网格细化方法求解该问题,取N= 8,Jmax= 8,ε=10-3。网格细化算法迭代5次中止,从2049个均匀节点中选用43个节点高精度逼近解析解,总耗时1.13 s。图 2给出优化的控制变量,为了对比,图中给出了解析解。本文优化的目标函数为11.11111101,与解析最优解(100/9)的前6位小数相同。图 3给出网格细化的迭代过程,其中竖直虚线为理论切换点位置。可见,在网格细化迭代过程中,离散点在切换点附近逐渐加密。

需要说明的是,表1中的hp方法2的耗时与本文方法也比较接近,尽管其采用的节点数目将近是本文方法的2倍。这是因为优化耗时除了与网格迭代次数和节点数目相关,还与NLP的稀疏特性以及偏导数的计算方法等因素有关,hp方法[13-14]集成了这方面的研究成果[21]。本文方法若应用这方面的研究成果,其优化效率也可以进一步提高。
4.2 算例2:月球着落问题
本算例研究月球软着陆最优控制问题[13]。该问题描述如下:最小化目标函数

(18)
并且满足状态方程

(19)
边界条件
[h(0),v(0),h(tf),v(tf)]=(10,-2,0,0)
(20)
控制变量约束
umin≤u≤umax
(21)
式中:umin= 0,umax= 3,g= 1.5,tf自由。该问题同样具有解析最优解,具体参见文献[13]。
采用本文方法求解该问题,取参数N= 8,Jmax= 10,ε=10-3。网格细化算法迭代6次中止,从8193个均匀节点中选用26个节点逼近解析解,总耗时0.15 s。图 4给出优化的控制变量。为了对比,图中给出了解析解。由图4中的局部放大图可知,本文方法准确捕捉住控制变量切换点位置。图 5给出了网格细化过程,其中竖直虚线为解析切换点的位置。可见,随着网格迭代细化,位于平坦区域的多余节点被及时删除,新增节点逐渐向切换点聚集。
为了对比,表2统计了文献中不同网格细化方法求解该问题的结果。其中,hp方法和h方法的结果与参数设置有关,表中只列出了最佳设置的结果。可见,与hp方法或h方法相比,本文方法的优化精度更高,并且网格迭代次数和节点数目显著减少。因而本文方法的优化耗时更短,尽管本文没有利用NLP的稀疏性并且采用的计算机主频更低(文献[13-14]采用的计算机主频分别为2.0 GHz和2.5 GHz)。另外,表中还给出了本文采用IMRT[10]求解该算例的结果。可见,与IMRT相比,本文的细化方法将节点数目减小31.2%,从而进一步减小优化耗时。该算例再次验证了本文方法的优势。
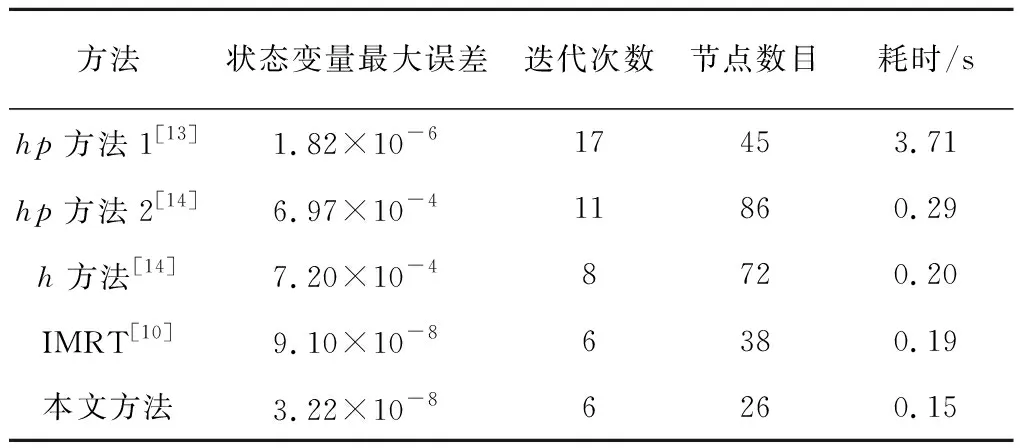
方法状态变量最大误差迭代次数节点数目耗时/shp方法1[13]1.82×10-617453.71hp方法2[14]6.97×10-411860.29h方法[14]7.20×10-48720.20IMRT[10]9.10×10-86380.19本文方法3.22×10-86260.15
4.3 航天器姿态调整问题
本算例研究航天器最短时间姿态调整问题。假设航天器为刚体,采用四元数法描述的航天器姿态动力学方程组(即状态方程)如下[18]
(22)
式中:q=[q1,q2,q3,q4]T为四元数,ω=[ω1,ω2,ω3]T为旋转角速度,u=[u1,u2,u3]T为控制力矩,转动惯量Ix=5621 kg·m2,Iy=4547 kg·m2,Iz=2364 kg·m2。
路径约束
(23)
控制变量约束
(24)
边界约束(初始条件和终端约束)
(25)
式中:φ为欧拉特征轴旋转角,φ=150°。
目标函数
J[x(t),u(t),tf]=tf
(26)
采用本文的网格细化方法求解该问题,取参数N= 20,Jmax= 8,ε= 10-3。本算例中特意选取N使其不等于2j(j为非负整数)。网格细化算法迭代5次中止,从5121个均匀节点中选用102个节点求解最优控制,最优目标函数为28.630387 s,优化耗时2.79 s。图6给出优化的控制变量和相应的节点分布。由图6(b)可知(注意图中的局部放大图),本文方法在每个切换点附近都达到了预期的最高分辨率(节点间距越小,分辨率越高),避免了细化遗漏或者细化失败,从而准确捕捉住控制变量的切换点位置(图中竖直虚线所示)。图 7给出了网格迭代过程,图中竖直虚线为最优控制变量的切换点位置。
为了对比,表3给出本文方法和文献方法[3,10]求解该问题的结果。其中,二代小波算法[3]从2049个均匀节点中选取187个节点,IMRT[10]从2561个均匀节点中选取121个节点。显然,本文方法采用的节点数目最少但是分辨率最高(用于选取离散节点的均匀节点基数越大,分辨率越高)。研究表明[10],提高分辨率能够减小终端约束的误差。与二代小波算法相比,本文方法的网格迭代次数和节点数都显著减少,并且对初始网格的节点数没有限制(二代小波算法要求初始网格的节点数为2j+1)。与IMRT相比,本文的网格细化方法更简单,并且将网格节点数目减少约16%,从而减少优化耗时。
从上述三个算例可以看出,本文的网格细化方法能够采用较少的离散节点高精度求解轨迹优化问题。本文方法原理简单、易操作,特别是提出的节点插入算法不需要采用多分辨率技术的多层次结构就能够持续细化网格直至满足精度或者达到最高分辨率,避免了细化遗漏或者失败,并且由于在计算插值误差时充分利用了网格信息,使得插入的节点数量较少,减小了优化计算量。此外,该方法对初始网格的节点数目没有限制。本文方法的不足之处是目前采用的节点删除算法只能删除斜率为零的节点。对于最优控制变量含有常值分量的轨迹优化问题(比如Bang-Bang控制问题,本文中的算例都属于这一类),本文方法的优化效率较高。与之对比,多分辨率技术及其改进形式[5-10]更适合求解最优解不含常值分量的轨迹优化问题。对于最优解不含常值分量的问题,虽然本文方法也能够求解,但是由于不能删除多余节点,可能会导致节点数量较多。当然,这种缺陷是由于节点删除算法的局限性造成的,未来若能设计出高效的节点删除算法,那么将有效扩展本文的节点插入算法的适用性。
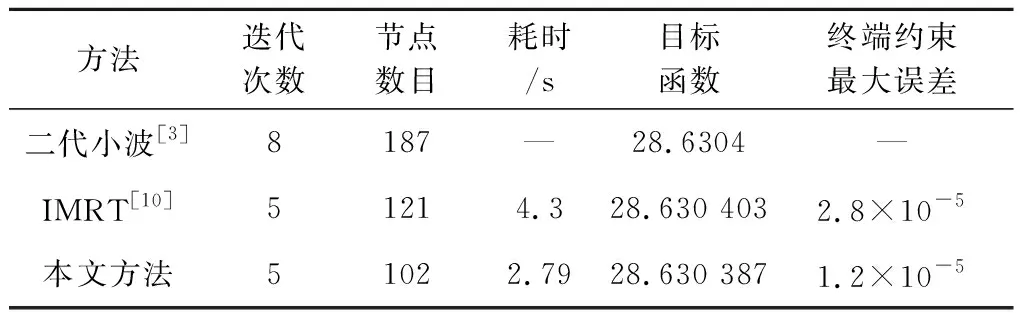
方法迭代次数节点数目耗时/s目标函数终端约束最大误差二代小波[3]8187—28.6304—IMRT[10]51214.328.630 4032.8×10-5本文方法51022.7928.630 3871.2×10-5
5 结 论
本文提出了一种基于插值误差和斜率分析的轨迹优化自适应网格细化方法。该方法采用局部配点法将轨迹优化问题转化为NLP,通过分析每个离散节点处的控制变量插值误差判断是否需要在该节点附近加密网格,通过计算每个离散节点处的控制变量斜率判断是否可以删除相应节点。采用三个轨迹优化算例验证了方法的有效性和特色。仿真结果表明,与文献中的网格细化方法相比,本文方法生成的网格规模更小,甚至需要更少的网格迭代次数,能够快速、高精度求解最优控制变量含有常值分量的轨迹优化问题。本文方法的不足之处是采用的节点删除算法只能删除斜率为零的节点。未来研究中需要设计更加通用高效的节点删除算法。
