导航星座整网自主定轨的动力学短弧段伪逆平差法

李灏霖，王 玲，黄文德，周一帆

(1. 湖南大学电气与信息工程学院，长沙 410012；2. 国防科技大学机电工程与自动化学院，长沙 410073； 3. 中国科学院上海天文台，上海 200030)

0 引 言

随着我国“北斗三号”全球卫星导航系统建设的推进，导航星座借助星间链路实现自主运行的研究也成为了当前导航领域的研究热点[1-3]。

由于星间链路是存在于导航卫星之间的相对测量，在没有外部基准的情况下，仅通过星间观测进行星座整网位置平差，会出现秩亏问题，无法实现星座的绝对定向和定位。为了解决秩亏问题，蔡志武等[4]提出了解决星座自主定轨基准秩亏问题的参数约束方法及星间测角资料辅助法。文献[5]采用借助中继星进行联合定轨的策略，消除秩亏及轨道整体漂移问题。文献[6-7]利用上注星历作为升交点先验信息，提供位置基准约束，进行自主定轨。文献[8]中采用增加地面锚固站的方法提供基准。上述方法主要通过外部基准或者精确的地面先验信息解决秩亏问题，当外部基准不可用或者先验信息精度不满足要求时存在一定局限性。另一方面，仅采用单历元距离观测进行星座整网平差时，无法对速度分量进行有效估计。文献[9-10]对该现象进行了简单阐述，并指出通过增加速度观测或动力学处理方法解决，但没有进行展开分析。

本文提出一种自由网伪逆平差理论和动力学短弧定轨技术相结合的自主定轨算法。采用大地测量平差中附加最小范数条件的最小二乘方法，即伪逆平差法解决整网位置解算起算数据不足带来的秩亏问题；采用动力学短弧定轨方法，通过状态转移矩阵和敏感矩阵建立观测值与待估参数之间的关系解决速度估计问题。以典型Walker导航星座为例，仿真了全星座星间链路测量数据，对算法性能进行了校验。

1 问题描述

1.1 导航卫星整网定轨模型

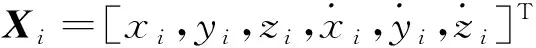
Li,j=h(Xi,Xj)=

(1)

式中:ε为星间测量误差。

(2)

(3)

(4)

式中:Vi,j为测量残差，A为系数矩阵。仅采用单历元观测数据进行定轨时，A可展开为

(5)

其中，

(6)

通过以上步骤的线性化，已经将观测数据和待估量的形式统一到定轨的残差模型中

V=AδX-l

(7)

残差最小二乘原理通过求取最小化误差的平方和寻找超定方程的解，即

(8)

其中，P为观测权矩阵。根据式(8)可以得到法方程

NδX-U=0

(9)

结果为

δX=N-1U

(9)

式中:N=ATPA，U=ATPl。

1.2 整网位置解算的秩亏问题

在有地面站或锚固站支持的情况下，卫星整网定轨以地面站作为定轨网络中的基准，式(9)能够得到一组唯一的最优解。但是，在自主运行模式下，卫星导航系统脱离地面运行。由式(5)的系数矩阵可知，当两颗卫星的测量为相对测量时，矩阵中对应行的这两颗卫星的线性化偏导数互为相反数。因而，整网观测中，所有卫星之间都存在着相关性。当没有外部基准且星座的所有节点的位置均未知时，会因为缺少必要的起算数据使得系数矩阵A列秩亏，进而导致法方程系数矩阵N秩亏，无法通过常规计算对N求逆。因此，由于星间观测对卫星网整体运动的不可观测性，其卫星网只能构成空间的相对位置约束，整个卫星网缺乏一个绝对的参考基准，法方程系数矩阵秩亏，只通过经典自由网平差无法得到最小二乘准则下的唯一解。

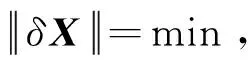
1.3 整网平差速度改正的问题

由式(1)可知,

仅利用单历元距离观测数据进行整网平差时，没有对速度的直接或间接观测数据,观测值对速度的偏导数均为0，即

因此，在对卫星状态的修正值δX的求解中，无法得到速度修正值，导致速度概略状态无法修正。文献[9]提出两种求取速度修正值的方法：1)星间观测仅采用测距信息，对卫星位置状态修正值进行求取，利用动力学方程获得速度修正值。2)星间观测增加测速信息。

目前，卫星导航系统多采用基于时间到达原理的星间距离测量作为星间链路的基本观测数据。同时，由于同轨道面卫星相对速度小，利用多普勒频移进行速度的相对测量精度较低，并不能满足速度状态更新的要求。因此，本文采用短弧段定轨，利用动力学模型求解状态转移矩阵，通过位置状态间接估计速度状态从而实现高精度定轨。

2 导航星座动力学短弧段整网平差定轨

2.1 伪逆平差方法

在起算数据不足的情况下，通过经典自由网平差无法得到最小二乘准则下的唯一解。下面给出利用伪逆平差得到秩亏方程的解的方法。

设满足法方程(9)的一个最小二乘解为

则该解的范数为

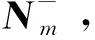
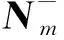
(10)

(11)

设矩阵N有一广义逆N+满足如下四个条件：

NN+N=N

(N+N)T=N+N

N+NN+=Ν+

(NN+)T=NN+

则称广义逆N+为N的伪逆。可见，伪逆因为满足最小范数逆的两个条件，所以为最小范数逆的一种，同样能得到的最小范数解

(12)

同时，伪逆N+唯一，可通过矩阵SVD分解求得。可以证明，δXm的协因数矩阵为

QX=N+NN+=N+

2.2 动力学短弧段整网平差

卫星的动力学模型可以表示为

(13)

式中:f为卫星的受力模型，对于中高轨道卫星一般考虑地球非球形摄动，日月引力摄动，太阳光压摄动等摄动因素，W为动力学模型噪声。将式(13)展开得

ΔW=F(t)·δX(t)+δW

(14)

式(14)的一般解为

δX(t)=Φ(t,t0)·δX(t0)

(15)

其中，Φ(t,t0)通过求解如下变分方程得到

且一般无法求得解析解，只能通过数值积分进行求解。

本文采用的短弧定轨的基本方法是，将某观测弧段上得到的PNum个历元的观测值通过状态转移矩阵归算到某一历元(例如该弧段的初始历元)。若观测采样间隔固定为TStep，则弧段长度TP满足

TP=(PNum-1)TStep

(16)

从当前弧段起始历元t0开始积分，得到弧段内t1,t2,…,tk,…,t(PNum-1)历元的概略状态及相对于起始历元的状态转移矩阵Φ(t1,t0),Φ(t2,t0),…,Φ(tk,t0),…,Φ(t(PNum-1),t0)。同时，通过t0,t1,…,tk,…,t(PNum-1)历元的观测数据，可以得到PNum组系数矩阵A(t0),A(t1),…,A(tk),…,A(t(PNum-1))。利用状态转移矩阵，将弧段内所有历元的系数矩阵统一归算至弧段起始历元t0，即

而通过式(15)中Φ(t,t0)和状态估计值的关系可知

(17)

所以

A(tk,t0)=A(tk)·Φ(t,t0)

(18)

由此，可以得到式(7)残差的变换形式

(19)

式中:δX(t0)为弧段起始历元整网所有卫星状态修正值。求出δX(t0)后，通过式(15)对弧段内其他历元的状态修正值δX(t)进行求解。

2.3 整网短弧段伪逆平差定轨算法流程

根据短弧段伪逆平差原理，首先确定弧段起始历元，并确定起始点的概略状态X-(t0)。然后进行整网短弧段伪逆平差定轨。整网短弧段伪逆平差定轨算法为本文研究的核心部分，主要包括短弧段数据累积、整网平差两部分，定轨算法及执行步骤如下所示。

步骤1：短弧段数据累积，包括以下步骤：

步骤1.1：获取弧段内起始历元的观测数据L(t0)，如式(1)，令k=1。

步骤1.2：如式(3)，求取起始历元的概略观测L-(t0)，同时，将起始历元观测数据L(t0)在X-(t0)处进行泰勒展开，得到起始历元系数矩阵A(t0)。

步骤1.3：通过轨道积分获得tk历元的概略位置X-(tk)以及该历元相对于弧段起始历元的状态转移矩阵Φ(tk,t0)。

步骤1.4：获得tk历元观测数据L(tk)。

步骤1.5：同步骤1.2，求取tk历元概略观测L-(tk)和系数矩阵A(tk)。

步骤1.6：通过式(18)，利用状态转移矩阵Φ(tk,t0)将历元系数矩阵归算至起始历元，得A(tk,t0)。

步骤1.7：判断tk是否为弧段终止历元，若不是，则k=k+1且返回步骤1.3。

步骤1.8：整合弧段内所有历元观测数据和概略观测可得矩阵L=[L(t0),L(t1), …,L(tk), …,L(t(PNum-1))]和矩阵L-=[L-(t0),L-(t1), …,L-(tk), …,L-(t(PNum-1))],从而可得残差矩阵l=L-L-，以及整弧段系数矩阵A=[A(t0,t0),A(t1,t0), …,A(tk,t0), …,A(t(PNum-1),t0)]。

步骤2：整网平差，包括以下步骤：

步骤2.1：构造如式(19)的最小二乘整网定轨模型，并得到法方程，如式(9)。

步骤2.2：对法矩阵N进行SVD分解，求得法矩阵的伪逆N+，并通过式(12)求得弧段内起始历元的状态修正值δX(t0)。

步骤2.3：通过式(15)，利用δX(t0)和状态转移矩阵Φ(t,t0)求取弧段内除起始历元外的其他历元的状态修正值，可得到δX，并加到概略位置上，得到全弧段轨道状态估计值。

3 仿真结果与分析

3.1 仿真算例

利用STK仿真卫星星座，Walker星座参数为24/6/1，所有卫星轨道统一高度为25678 km，轨道偏心率为0，轨道倾角55°，近地点角距为0°，其他初值不同的轨道6根数如表 1所示。动力学模型中，除地球中心引力外，还考虑10×10阶地球非球形摄动、日月引力摄动以及太阳光压摄动。其中，重力场模型采用JGM-3全球重力场模型；太阳光压模型采用球模型，面质比取0.002 m2/kg，反射系数取1.2，考虑锥形地影模型。本文仅进行卫星定轨，不进行钟差估计。

仿真起始历元，各卫星位置状态加入均方根为1 m正态分布的随机误差，速度加入均方根为10-6m/s正态分布的随机误差。同时，仿真的观测数据在理论距离的基础上加入均方根0.2 m的随机误差。

表1 星座轨道根数初值Table 1 Part of initial value of constellation

注：M表示对应卫星编号的平近点角； RAAN表示升交点经度。

3.2 结果分析

在进行整网定轨中以用户测距误差值(User range error,URE)作为定轨精度判定指标[11]，其定义为：

ΔURE(i)=

其中，ΔURE(i)表示第i颗卫星的URE值，R(i)表示径向方向误差，C(i)表示钟差误差，本文不对钟差进行估计，因而钟差为0，T(i)表示迹向方向误差，N(i)表示与径向、迹向平面垂直方向的误差，ΔUREM表示星座中n颗卫星的平均URE值。

本文以15 min为一个历元，采用6历元一个弧段进行自主定轨。依据式(16)，对应弧段长度为75 min。

若不进行自主定轨，仅通过动力学模型进行轨道预报90天，误差如图 4所示，24颗卫星ΔUREM约600 m。

图5为采用本文自主定轨算法运行90天，不同历元24颗卫星ΔUREM。从图 5可以看出，卫星整网星座自主运行90天，定轨结果未发现明显的发散过程，定轨精度稳定，ΔUREM曲线下包络精度基本控制在0.5 m以下。经统计，24颗卫星ΔUREM，90天的均值为0.54 m，标准差为0.23 m，其中最大值为1.98 m，最小值仅0.054 m。

从图6可以看出，RTN三个方向误差都比较稳定，与ΔUREM的变化趋势基本一致，T方向误差变化比较明显，是导致ΔUREM曲线下包络变化的主要原因。

4 结束语

本文针对传统静态自由网平差进行自主定轨存在的秩亏问题，提出一种自由网伪逆平差理论和动力学短弧段定轨技术相结合的自主定轨算法。该算法在传统最小二乘解算的通解基础上增加最小范数约束得到唯一位置解，解决整网位置解算起算数据不足带来的秩亏问题；同时，利用状态转移矩阵对系数矩阵进行归算，通过距离观测间接修正速度，解决单历元平差无法对速度分量进行有效估计的问题。本文方法可应用于我国“北斗三号”全球卫星导航系统的自主运行。