基于FDM的低熔点金属牙模制备方法研究

杜云飞,宁会峰,2,阎相忠

(1.兰州理工大学机电工程学院，甘肃 兰州 730050) (2.兰州理工大学数学制造技术与应用省部共建教育部重点实验室，甘肃 兰州 730050)

目前，义齿制作方法主要有熔模铸造和机械CAD/CAM技术。熔模铸造工艺复杂且产品质量容易受到影响，其中蜡型的制作对后续铸造性能影响很大，其质量直接决定义齿加工质量；CAD/CAM 技术由于切削的材料是强度和硬度都非常高的陶瓷块，切削难度大且工艺要求高，而且基于减法制造的切削技术也造成了材料的浪费，材料利用率和加工效率都不高[1-2]。

近几年，随着3D打印技术的应用与发展，将3D打印技术应用于传统义齿制造过程中，能否在一定程度上提高义齿模型的加工效率、缩短工艺流程、提高义齿质量、降低加工成本具有重要意义，有必要进行深入研究。目前，使用低熔点金属制作模型具有制作工艺简单、制作周期短以及制作成本低等特点，已经被认为是一种比较合理的模具制作方式，是模具行业的一种新的制作工艺和技术。本文主要以低熔点金属为材料，应用熔融沉积成型技术(FDM)制作可用于熔模铸造的义齿模型。

1 FDM成型过程中丝材受力分析

FDM-3D成型设备的喷头和送丝机构共同构成设备的熔挤机构，FDM成型过程中由滚轮和丝材之间的摩擦力f提供进给力，驱动丝材顺利、准确地进入喷嘴内腔并受热融化，再通过喷嘴挤出并沉积于工作台上凝固成型。图1所示为FDM送丝机构驱动力示意图。

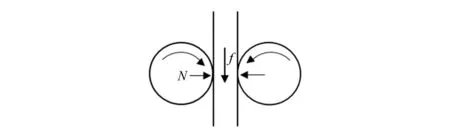
图1 FDM驱动轮与驱动力

在FDM成型过程中，送丝机构能否提供足够的驱动力是丝材能否顺利挤出成型的重要因素，现有的FDM打印机都是通过电机带动驱动轮，通过驱动轮和从动轮与丝材之间的摩擦力驱动丝材进给，其中进给力等于摩擦力f[3]。

假设驱动轮提供的进给力为F1，熔融材料从喷头中挤出所需克服阻力为F2，当F1小于F2时，送丝机构所提供的驱动力将小于喷头对丝材挤出时的阻力，此时会造成驱动轮与丝材之间相对滑动的现象，使丝材进给量和出丝量减少，严重影响出丝质量和成型质量。因此，只有驱动轮与丝材之间的摩擦力F1大于喷头对丝材的阻力F2时，才能保证送丝与出丝质量，保证成型质量[4]。图2为丝材进给与挤出过程中的受力图。

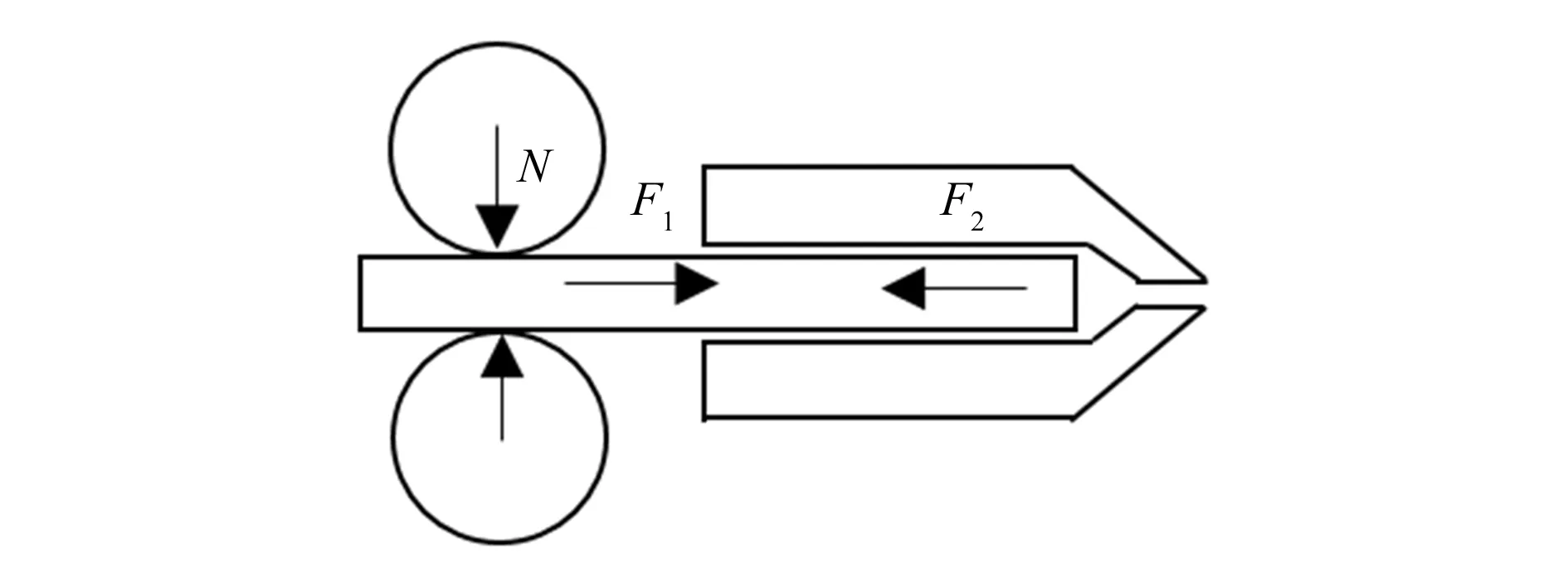
图2 进给与挤出过程中丝材受力图

1.1 驱动轮对丝材的驱动力

FDM打印过程中驱动轮之间的间隙决定摩擦力f的大小，在计算时需要考虑丝材在驱动轮之间挤压变形所产生的弹性变形力N[5]。摩擦力f的计算公式为：

f=μ·N

(1)

式中：μ为材料与送丝滚轮之间的摩擦系数。

N=k·ΔX

(2)

式中：ΔX为挤压变形量；k为劲度系数。k的计算公式为：

(3)

式中：E为材料的弹性模量；S为材料的横截面积；D0为材料的原长。

结合式(2)和式(3)可得送丝过程中材料在驱动轮之间挤压变形产生的弹性力为：

(4)

驱动轮所产生的驱动进给力为丝材与驱动轮之间的摩擦力f，结合式(1)和式(4)，则进给力F1为：

(5)

1.2 丝材挤出时的喷头阻力

FDM成型过程中，熔融丝材主要靠未融化的丝材提供的向下的挤压力挤出，此时未熔融的丝材将喷头中的熔融丝材不断挤出。驱动轮对丝材提供的进给力能否克服喷嘴流道中熔融丝材的挤出阻力直接关系到打印过程中丝材能否顺利挤出，而熔融丝材在喷嘴流道中的挤出阻力主要取决于熔融丝材本身的黏度、挤出速度和流道的尺寸[6]。

流体流动过程中具有内摩擦力是产生流动阻力的内在原因，而流体的黏性是流体内摩擦力的体现，黏度作为衡量流体黏性大小的物理量，流体黏度越大其流动性能就越差，相应的流动阻力越大。熔融材料在喷管中的流动，可以看作是无数极薄的圆筒状层流体，每一层流体以不同的速度向前流动，层与层之间存在阻滞剪切变形的黏性力。图3为喷管中熔融材料分层流动示意图。

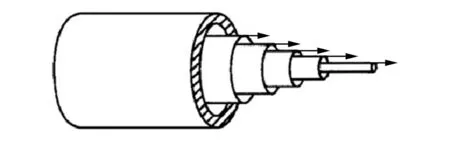
图3 材料分层流动示意图

根据牛顿的总结，可知对于某一种流体，内摩擦力F与两流体层间的速度差u成正比，与两流层间的接触面积A成正比，而与两流层间的垂直距离y成反比。FDM成型过程中喷嘴中的熔融材料属于黏塑性流体，当进给力F1满足挤出条件时其流动与牛顿型流体一致。根据牛顿黏性定律，熔融丝材挤出过程中的挤出阻力可表示为：

(6)

式中：du/dy为流体垂直于速度方向的速度变化率；A为接触面积；η为流体黏性的比例系数，简称黏度。

2 喷头温度对丝材受力情况的影响分析

2.1 喷头温度对进给力的影响分析

FDM成型过程中驱动轮挤压材料所产生的弹性变形力对于驱动进给力有直接影响。在FDM成型过程中，由于喷头整体结构紧凑，在满足打印温度时喷头温度场的传递情况会十分明显，主要为由喷头热端向喷头支架及送丝机构传递。材料在喷头温度场的影响下会使丝材自身温度升高，从而引起材料弹性模量的变化，对进给力有直接影响。

查阅文献[7]、[8]可得，弹性模量与温度之间的关系可以用式(7)表示。

E1=E0(1-αE·Δt)

(7)

式中：E1为温度为t时物体的弹性模量；E0为标准温度t0(常温环境20℃)时物体的弹性模量；αE为物体弹性模量的温度系数；Δt为温度差，Δt=t-t0。

结合式(5)和式(7)，可得在温度影响丝材弹性模量的情况下，滚轮对丝材提供的驱动力为：

(8)

由此可见，温度的升高会引起材料本身弹性模量E直线下降，造成打印过程中进给力减小，影响出丝速度和精度。

2.2 温度对喷嘴挤出压力的影响分析

温度对流体黏度有较大影响，对于黏流状丝材而言，相关研究表明：随着温度的升高材料黏度明显下降，黏度η与温度T之间的关系满足Arrhenius定律，故可用Arrhenius方程对其进行表述[6,9-10]，即：

η=λeΔEη/RT

(9)

式中：λ为常数，主要与材料的分子结构有关；ΔEη为黏流活化能；R为气体常数，R=8.314J·mol-1·K-1；T为热力学温度。

结合式(6)和式(9)可得，对于同一种打印丝材，选择不同的温度作为打印温度，则喷头中熔融丝材的挤出阻力不同，其表达式为：

(10)

结合丝材受力进行分析，在挤出过程中，驱动轮对丝材的驱动力F1要大于熔融丝材在喷头流道中的挤出阻力F2，才能实现丝材顺利挤出。因此，在一定打印温度下应满足丝材所受的合力F=F1-F2>0，结合式(8)和式(10)得：

(11)

3 FDM喷头温度场有限元分析

3.1 FDM喷头温度控制要求

本文选择以聚丙交酯(PLA)材料为基料并加入金属材料混合而成的低熔点金属材料作为原材料。在打印温度保持在230℃～240℃时，该材料具有较好的打印性能；当温度小于230℃时，材料从喷嘴中挤出不顺畅，对成型件表面质量有较大影响；温度高于240℃时，材料容易分解，材料从喷嘴挤出后在工作平台上的黏结性能较差。从温度控制要求的角度来看，根据热传递情况和FDM喷头结构与功能，需要达到以下2个目的：

1)为了保证打印过程的连续性，需要将喷头温度控制在230℃～240℃，并保证喷嘴流道具有稳定的温度环境。

2)对于所选用的低熔点金属材料，其受热变形温度为90℃～120℃，要保证导向管中的丝材保持一定的硬度来提供进给力，在进给机构进给滚轮处的丝材温度不得高于60℃。

3.2 FDM喷头温度场有限元分析

本文采用ANSYS Workbench对喷头温度场进行分析，分析过程以热传导和热对流为主。热传导是发生于喷头结构各个零部件之间的热量流动。热对流分析主要有空气冷却和风冷，其中电阻式加热部分以自然环境的空气冷却为主，而安装于送丝机构上的风扇则是对送丝机构的对应面提供强对流风冷。

1)建立喷头结构模型。

进行喷头温度场分析时，在不影响计算结果的前提下，可简化几何模型，这样做有利于网格的划分，并能降低计算强度。经简化后的喷头结构几何模型如图4所示。

图4 喷头结构简化图

2)定义喷头系统各部分材料属性。

材料属性的设置中，主要包括材料的密度(kg/m3)、弹性模量(N/m2)、泊松比、比热容(J/(kg·K))和热导率(w/(m·K))。喷头各个部分主要由铜、铝合金等材料制成，可以在ANSYS Workbench材料库中直接选择材料属性；低熔点金属材料的各项属性见表1。

表1 低熔点金属材料属性

3)几何模型网格划分。

采用Meshing网格划分平台进行网格划分后得到的喷头结构如图5所示。

4)施加载荷。

分析过程中，热载荷施加于喷头末端电阻式加热块位置，载荷设置为240℃；加热块对流系数设置为100W/(m2·K)；散热机构对流系数设置为200W/(m2·K)。

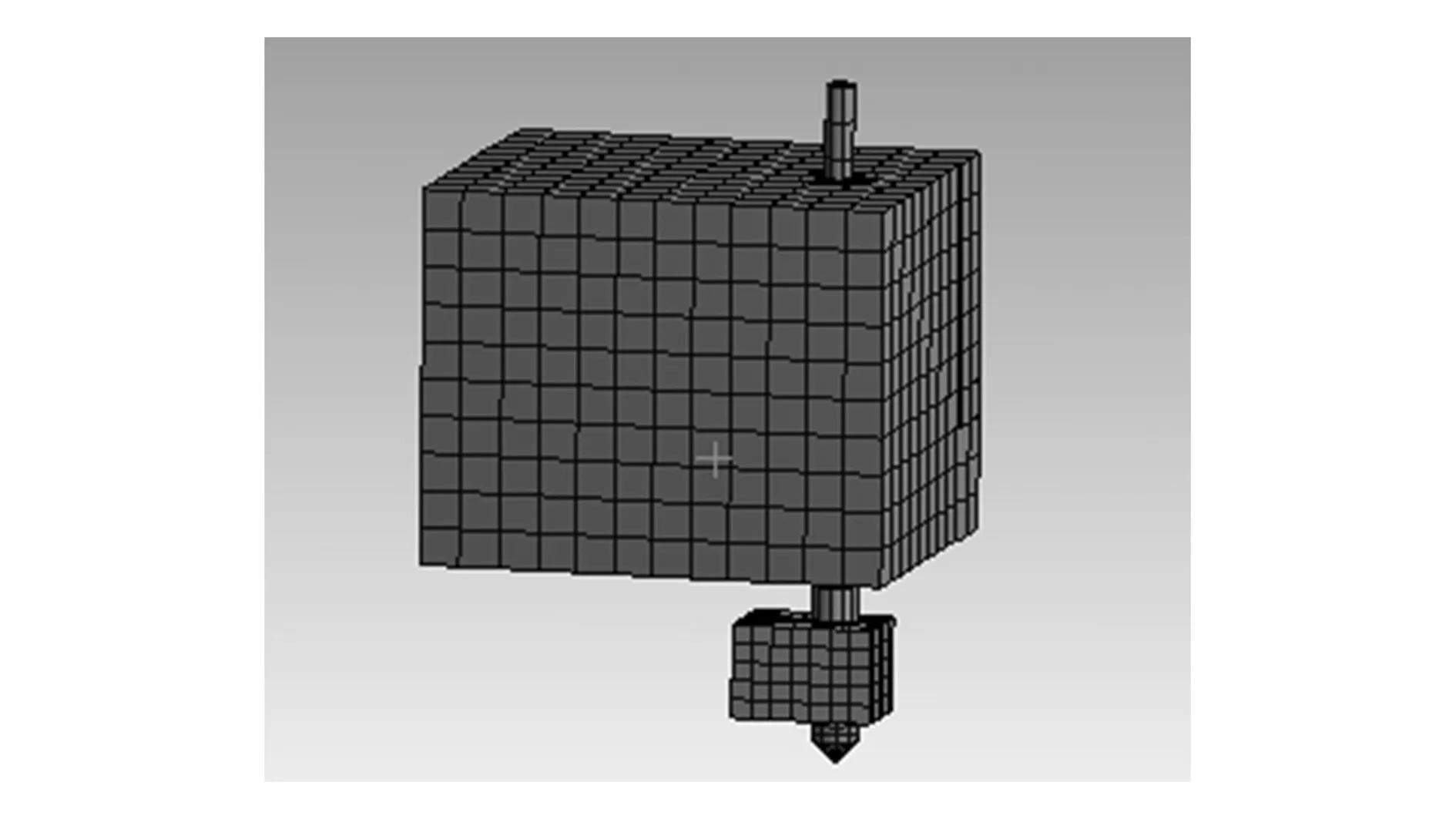
图5 喷头结构网格划分图

5)求解与后处理。

经过求解与后处理所得喷头结构温度场分布和丝材温度传递情况分别如图6和图7所示。

图6 喷头系统温度场分布图

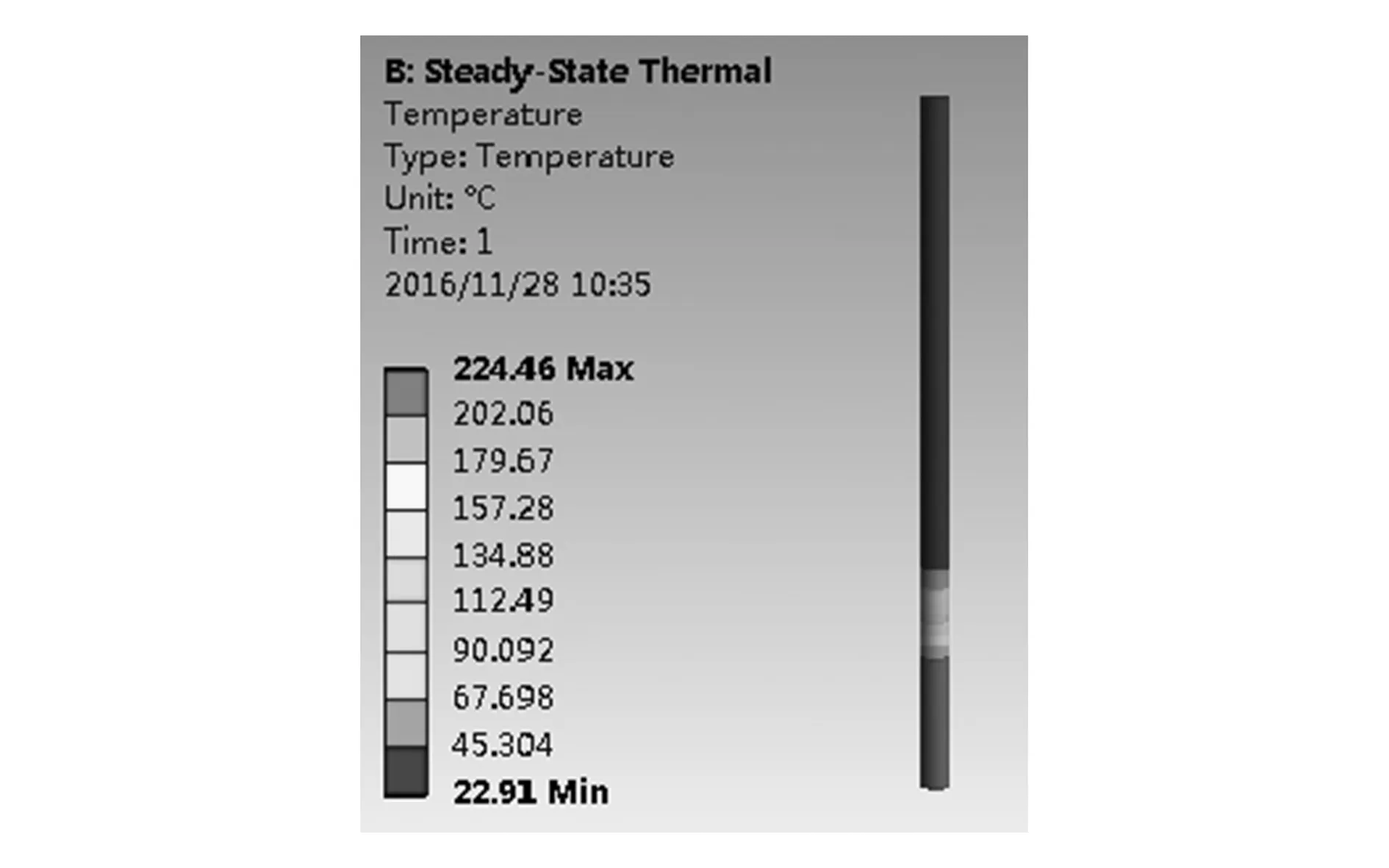
图7 丝材温度传递图

由分析结果可知，FDM成型过程中送丝机构部分能够保持室温状态；丝材温度场主要分布于喷头处，向上的传递区域较小，在送丝滚轮部分的丝材温度保持在23℃左右，满足在进给滚轮处丝材温度不得高于60℃的要求，可忽略温度场分布对进给力的影响。

3.3 FDM喷头挤出阻力有限元分析

本文选用的低熔点金属材料的打印温度为230℃～240℃，分别测定该材料在230℃、235℃和240℃时的材料黏度，测定结果见表2。

表2 低熔点金属材料黏度

在不同打印温度下熔融材料的黏度不同，对FDM喷头出口处的挤出阻力进行有限元分析时，分别设定材料黏度为1 200Pa·s、900Pa·s和700Pa·s，对材料从喷头中挤出时喷嘴出口处的压强进行有限元分析，计算得出对应打印温度下所需的挤出阻力。

采用ANSYS Workbench-CFD模块对喷头中熔融丝材的挤出进行流体力学分析，首先建立喷管几何模型，然后对几何模型进行网格划分，并添加熔融材料黏度属性，最后通过有限元计算与分析得到材料从喷嘴挤出时喷口处的压强分布图。喷管几何模型和几何模型的网格划分如图8和图9所示。

图8 喷管几何模型图

图9 喷管网格划分图

经过有限元分析得到对应黏度下喷嘴出口处压强分布情况，分别如图10、图11和图12所示。

由压力分布云图可得：在材料黏度为1 200Pa·s时，喷口处的最大压强为7.033×106Pa；在材料黏度为900Pa·s时，喷口处的最大压强为5.278×106Pa；在材料黏度为700Pa·s时，喷口处的最大压强为4.109×106Pa。

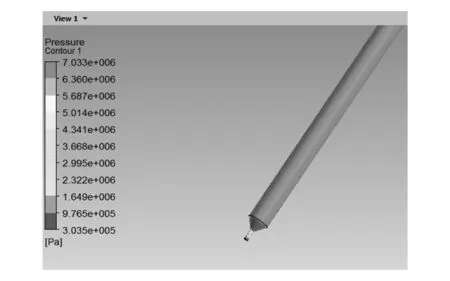
图10 材料黏度为1 200Pa·s时喷嘴压强分布图

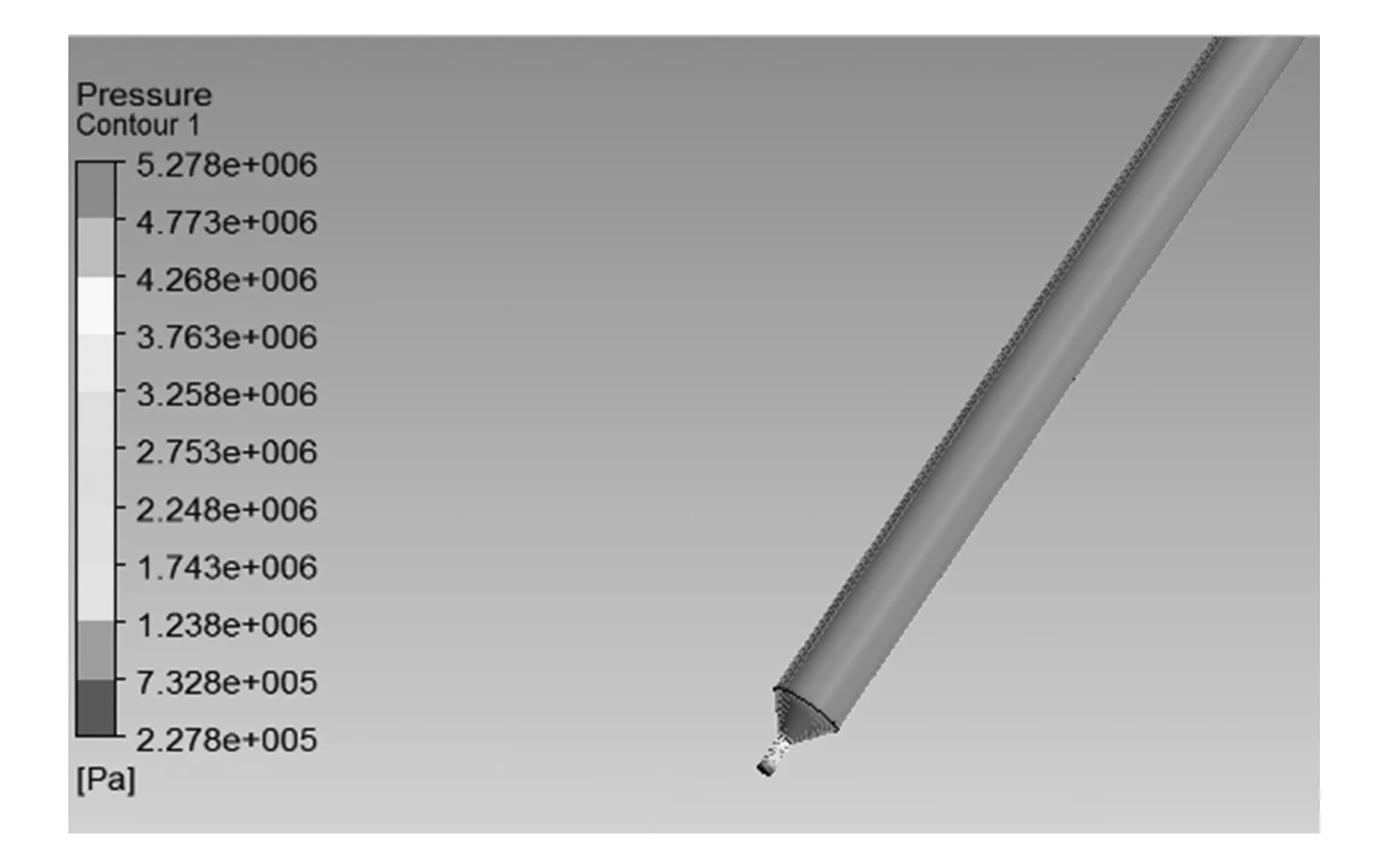
图11 材料黏度为900Pa·s时喷嘴压强分布图

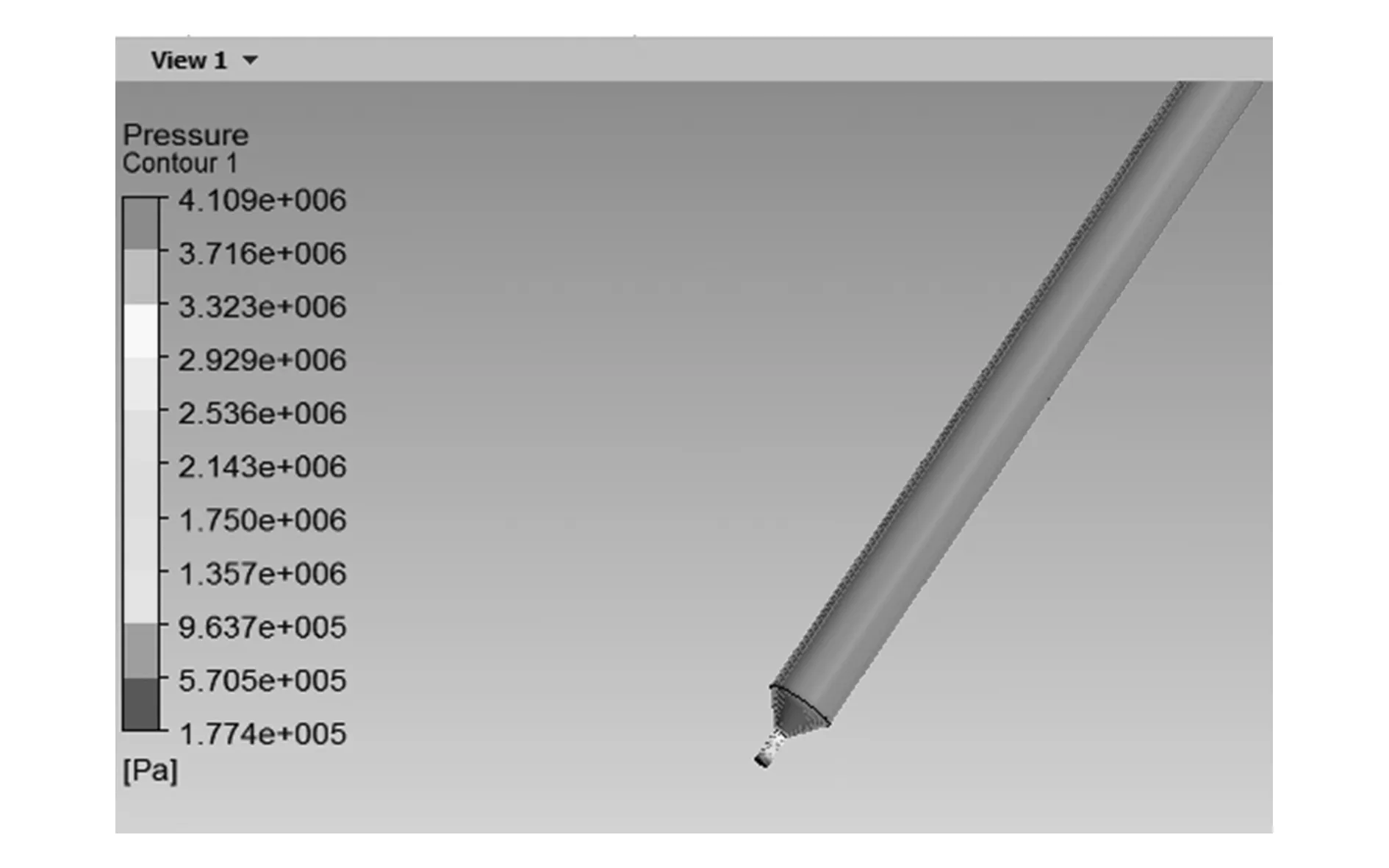
图12 材料黏度为700Pa·s时喷嘴压强分布图

喷口处的挤出阻力由F2=P·S(其中P为压强)计算可得：在1 200Pa·s时为49.78N；在900Pa·s时为37.26N；在700Pa·s时为29.03N。丝材挤出力由驱动轮与丝材之间的摩擦力提供，由进给力F1=μ·N(μ=0.018)，可得各个打印温度下丝材受驱动轮挤压变形所产生的最小弹性变形力与挤出阻力之间的对应关系，见表3。

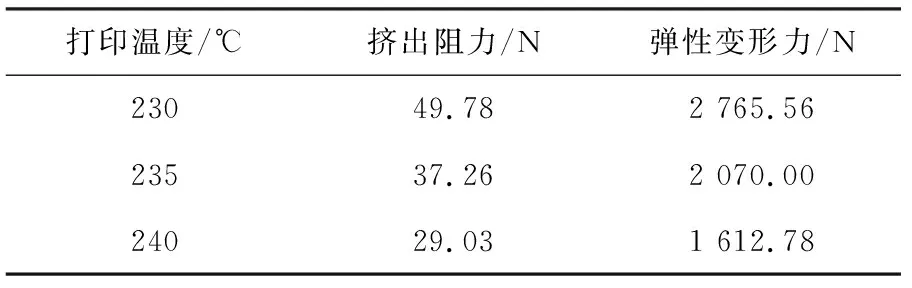
表3 挤出阻力与丝材弹性变形力

在230℃～240℃的打印温度下，送丝滚轮部分与丝材温度保持在23℃左右，所选用的低熔点金属材料在常温下的弹性模量为0.37GPa，其劲度系数为：

丝材在送丝滚轮夹持作用下所产生的弹性变形力N为：

N=k×ΔX=5 082 875×0.000 75=3 812.16(N)

滚轮可提供的进给力F1为：

F1=f=μ·N=0.018×3 812.16=68.62(N)

综合以上分析和计算，可见当打印温度在230℃～240℃时，随着打印温度的升高，丝材挤出阻力逐渐减小。在230℃时需要的挤出力最大，为49.78N；在240℃时需要的挤出力最小，为29.03N。送丝机构在该打印温度范围内能够提供的送丝进给力通过计算为68.62N，可以满足进给力F1大于挤出阻力F2这一挤出条件，可以顺利进给并挤出丝材。因此，选择230℃～240℃的打印温度范围是合理的。

4 基于FDM的低熔点金属牙模制备实验

4.1 几何模型建立与分层处理

运用FDM成型技术制造牙齿模型时，首先要建立牙齿几何模型，然后将几何模型保存为STL格式的数据模型并进行分层处理，随后将分层处理的数据模型输入到打印设备即可开始牙模制备工作。图13所示为使用Creo三维建模软件建立的上颌中切牙近似模型。

图13 上颌中切牙几何模型

在对几何模型进行分层处理时，分层厚度设置越小得到的牙模精度越高。分别设置0.1mm、0.2mm和0.3mm的分层厚度对模型进行分层处理，当分层厚度为0.1mm时分层模型共包含148层层面轮廓；当分层厚度为0.2mm时分层模型共包含75层层面轮廓；分层厚度为0.3mm时分层模型共包含51层层面轮廓。分层厚度越小，得到的分层模型越精细。

4.2 牙齿模型制备

上述工作完成后即可进行上颌中切牙模型的打印工作。

1)首先选择0.2mm分层厚度，分别设置230℃、235℃和240℃作为打印温度进行牙模制备工作。通过牙模制备实验发现在满足挤出条件的情况下，打印温度对于成型效果的影响主要集中在初始层的成型质量上，图14为不同打印温度下初始层的成型效果。

图14 不同打印温度下初始层成型效果图

由初始层成型效果可以看出：在230℃时，由于打印初始阶段熔融丝材黏度较大，底层成型存在明显缺陷；在235℃时，随着打印温度的升高熔融材料的黏度降低，但出丝直径较小，底层成型粗糙度明显；在240℃时，随着熔融丝材黏度的降低，出丝质量良好，底层成型质量得到明显提高。可见随着打印温度的提高，初始层的成型质量逐渐提高。因此，最终选择240℃作为打印温度。

2)分别设置0.1mm、0.2mm和0.3mm作为分层厚度进行牙模制备工作，不同层厚下最终制得的牙齿模型如图15所示。

图15 不同层厚的FDM牙齿模型

从图中可以看出，分层厚度的增加会使得成型面逐渐出现阶梯误差，在分层厚度达到0.3mm时，制件表面出现明显的阶梯效应。在制得牙齿模型后，通过Mitutoyo SJ400型表面粗糙度测量仪对牙齿模型表面粗糙度进行测量，测得不同分层厚度下制得的牙齿模型表面粗糙度(Ra)，见表4。

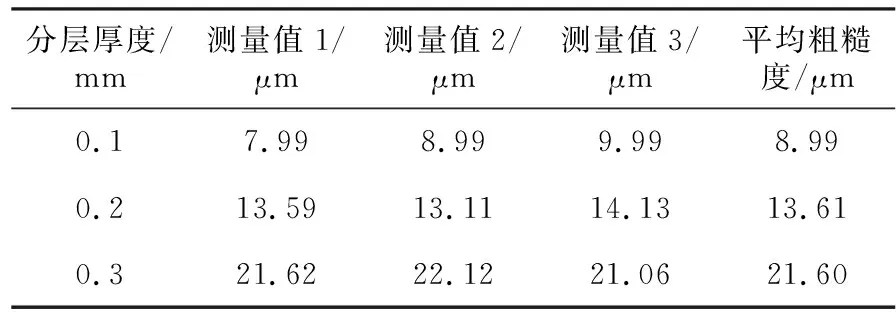
表4 牙齿模型表面粗糙度

通过对牙模制件表面质量的分析可以看出：在分层厚度为0.1mm和0.2mm时，表面质量较好，制件表面粗糙度比较接近，表面无明显的阶梯效应；分层厚度为0.3mm时表面质量较差，制件表面粗糙度明显增大，表面出现明显的阶梯效应。分层厚度越小成型质量越好，但是分层厚度越小所需要的打印时间越长，表5所示为分层厚度与分层数量以及成型时间之间的关系。

表5 分层厚度与分层数量及成型时间

综合考虑成型质量和成型时间，可以选择0.2mm层厚作为后期牙模制备时的分层厚度，并将该分层厚度下制得的牙齿模型作为最终产品。

5 结束语

本文在FDM成型技术的基本原理上对FDM成型过程中丝材的受力情况进行理论分析，建立了丝材进给力和挤出阻力数学模型；并对温度场对丝材受力情况的影响进行分析，建立温度场影响下的丝材力学模型。同时，通过有限元仿真及实验确定出所选低熔点金属丝材的最佳成型温度，并最终制得牙齿模型。由于条件有限，本文对于基于FDM的低熔点金属成型技术的研究仍有一定的局限性，成型精度仍然不足，所制得的牙齿模型比较粗糙，如何提高成型精度的理论分析和实验验证有待进一步的研究。