六边形蜂窝铝异面动态冲击仿真研究

马思群，郝 月，孙彦彬，高 峰，徐天时，姚莉军

(1.大连交通大学机车车辆工程学院，辽宁 大连 116028) (2.中车唐山机车车辆有限公司，河北 唐山 064000)

蜂窝材料是孔隙结构有序的典型多胞材料之一，具有减振吸能、吸声、隔热、密度小、比强度和比刚度高等诸多独特的力学性能和物理性能，在耐碰撞和吸能装置中得到广泛使用[1]。由于异面压缩吸能特性要远远优于其在共面压缩时的特性，在诸多领域受撞击载体中主要应用蜂窝材料的异面结构。

在实验和有限元研究方面，Gibson等[2]对蜂窝材料受压溃时的力学性能做了详细研究，张菲菲、欧阳昊等[3-4]对蜂窝铝的压缩变型机制、能量吸收情况等做了大量研究，并且得出了共面力学特性的经验公式。根据胡玲玲等[5]的研究可知，对能量吸收起支配作用的是动态峰应力和密实化应变。目前在有限条件下对异面方向的动态峰应力的研究较少，因此研究六边形蜂窝铝异面碰撞时动态峰应力对能量吸收的影响显得尤为必要。本文尝试通过建立双壁厚蜂窝有限元模型，探究壁厚及冲击速度对蜂窝铝平台阶段动态峰应力以及在碰撞过程中吸能能力的影响，进而获得相应结论。

1 前处理及理论分析

商用金属蜂窝最显著的特点是孔壁厚度不均匀。其最常用的制作方式是用粘结剂粘贴成型的板材，然后将其沿垂直于板面方向拉开。如图1(a)所示，板材粘贴处在竖直孔壁上，因而竖直孔壁厚度是其他壁厚的两倍。图1(b)所示为六边形的蜂窝体，由该结构可以看出，蜂窝铝属于正交各向异性材料，到目前为止，这是用于缓冲吸能最普遍的一种材料。

本文选用的孔穴是正六边形，即h/l=1,扩展角θ=30°。本文中定义:h=l=3mm，x3方向上的长度L=40mm。模型的基体材料选用铝，其基本力学参数为:密度ρ=2 700kg/m3,弹性模量Es=68GPa，泊松比ν=0.35，屈服应力σy=0.3GPa。

图1 商用双壁厚蜂窝铝结构模型

在软件LS-DYNA中，基体模型选用24号材料模拟，刚性墙选用20号材料模拟。在整个动态冲击仿真过程中，将移动刚性墙和固定刚性墙置于蜂窝模型的两端，考虑到模型受到压溃时的接触状态，将其设置为自动单面接触，刚性墙与模型设置成自动面面接触。铝受到应变率的影响较小，因此在做前处理工作时暂不考虑应变率对模型的干扰。蜂窝材料在异面的压缩是集大应变、大位移于一身的复杂非线性问题，因此做好前处理工作是仿真分析成功与否的重要环节[6]。

蜂窝铝在工程中应用的范围较广，如既可应用其独特结构作为包装芯材保护贵重物品，也可利用其减振吸能的优异性能缓解动车组在高速状态下碰撞对乘客造成的冲击伤害，或用于保护航天飞行器使其零部件等结构免于因外界碰撞而造成损失。因此对蜂窝模型进行动态冲击仿真模拟过程中，将有限元模型设置了多个阶梯速度和阶梯壁厚以获得其在不同数值下的应力和能量值，并通过对比分析其在不同阶梯速度和壁厚下的走势和规律[7]。

2 后处理及计算结果分析

2.1 仿真结果分析方法

碰撞计算结束后，通过对从后处理软件LS-PREPOST直接获得的曲线的整合，可得到支反力与位移曲线(F-u)，总能量、内能、动能与位移曲线(T-u、I-u、K-u)。图2为v=90m/s、d=0.1mm时计算得到的曲线。由图2(b)可知，模型在碰撞吸能过程中，内能基本等于吸收的总能量，动能所占总吸能的比例不大(动能曲线是放大10倍后的图形)。

图2 异面碰撞后的能量曲线

在F-u曲线的线弹性阶段即将结束时，力会达到一个初始峰值，它对应的位移是初始位移u0；模型碰撞所获得的动能在平台阶段结束时会出现一个局部峰值(波峰或波谷)，对应的位移就是密实化位移ud。在T-u曲线上找到u0，ud二值对应下的能量E0，Ed，根据公式Fp=(Ed-E0)/(ud-u0)可以求得冲击力Fp，Fp与模型的横截面积s的比值就是动态峰应力[8]。

2.2 速度对峰应力的影响

图3为速度在30，70，110m/s时，d=0.25mm、l=3mm的蜂窝铝的力-位移图。从图中可以看出，在曲线的线弹性段力都会有一个初始峰值，该力在移动刚性墙与蜂窝铝初始接触时对压缩速度很敏感，速度越大，碰撞之后获取的反力值也越大；随后进入平台阶段，该阶段的力也随着压缩速度的增大而增大，平台阶段的波动是蜂窝层层坍塌导致的，且随着速度的增大，波动越来越明显；接着进入密实化阶段，该阶段支反力陡然上升，但吸能较少，随着压缩位移增加，蜂窝由于结构坍塌迅速被压成扁平状。

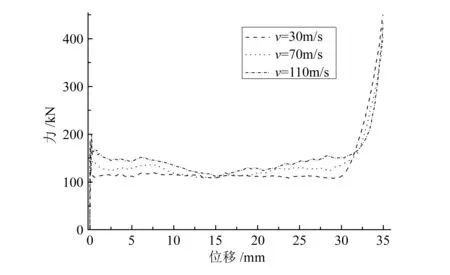
图3 d=0.25mm时六边形蜂窝铝3种速度 下支反力和压缩位移的关系曲线

将后处理计算得到的六边形金属蜂窝动态峰应力列于表1中，从表中的数据可以直观地看出随着速度和壁厚的增大，计算出的峰应力数值都是递增的。图4为当壁厚为固定值时通过软件MATLAB编程语言拟合出来的动态峰应力随速度变化的关系曲线。

由软件拟合可知，动态峰应力σ与速度υ的曲线形式与二次函数最为接近。计算公式为：

σ=Av2+Bv+C

(1)

式中：A，B为关系系数，由蜂窝的材料、结构和速度共同决定;C为静态峰应力。根据计算数据，通 过最小二乘法拟合可以得出，当壁厚分别为0.10，0.15，0.20，0.25，0.30，0.35，0.40mm时，动态峰应力与速度的曲线系数A，B，C分别为：0.08，50.4，7 985.6Pa；0.18，26.8，17 219.0Pa；0.20，49.7，26 254.0Pa；0.17，85.8，36 387.0Pa；0.22，95.8，49 293.0Pa；0.12，139.1，61 115.0Pa；0.19，135.4，75 435.0Pa。

表1 蜂窝铝在不同壁厚和速度下的动态峰应力 MPa

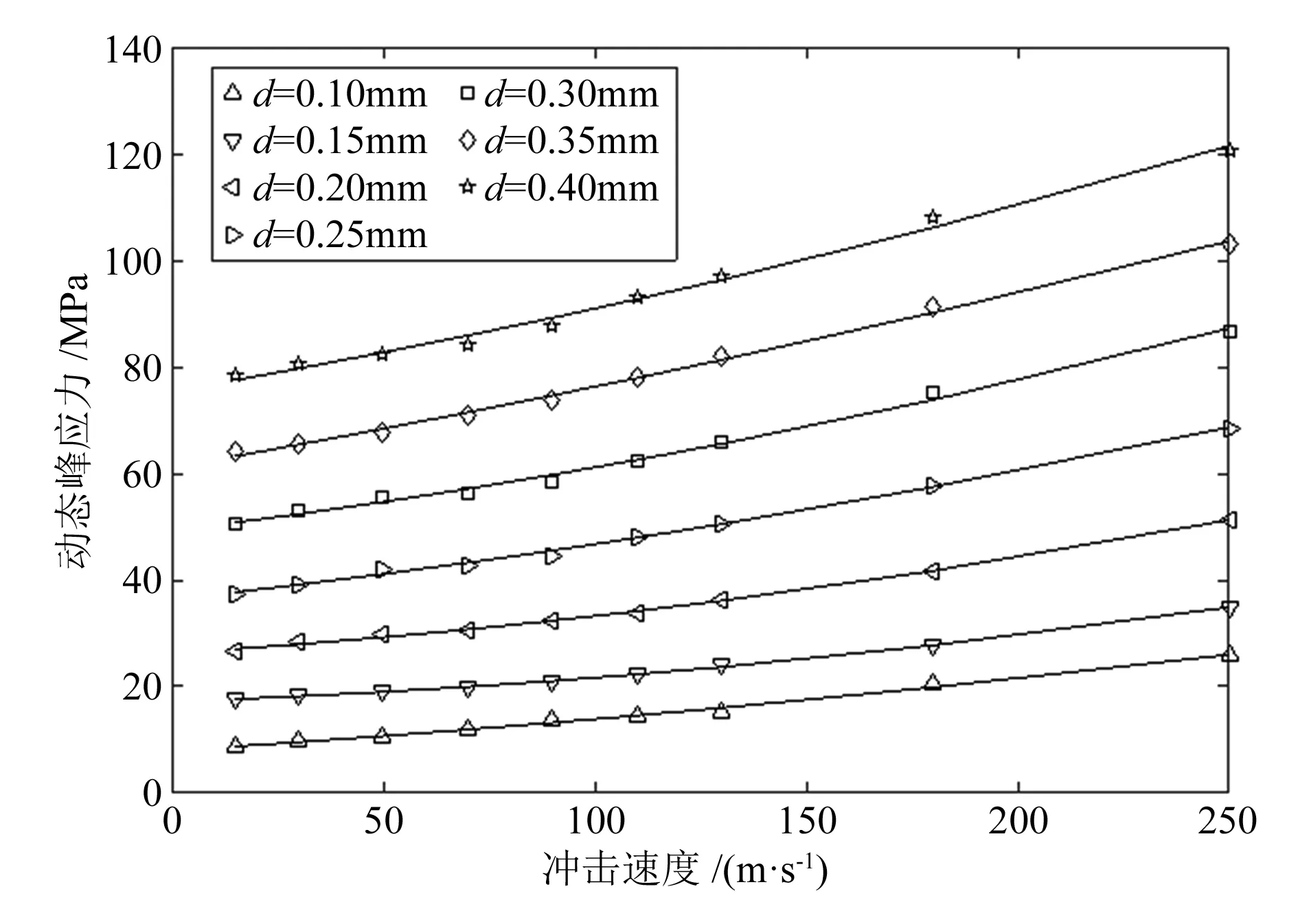
图4 不同壁厚时动态峰应力随速度变化的关系曲线

2.3 壁厚对峰应力的影响

图5是v=90m/s时六边形蜂窝铝3种壁厚下支反力和压缩位移的关系曲线。从图中可看出，在线弹性阶段，当速度保持一定时，支反力初始峰值不仅对速度很敏感，该值也颇受壁厚的影响；平台阶段，平台力随着壁厚的增大而增大，且上升的幅度逐渐变大，与此同时，由于壁厚增大而在轴向压缩时引起的波动也越来越明显；壁厚增大也导致了蜂窝铝被压溃时提前进入密实化阶段，使得密实化位移变小，从而间接影响平台阶段的平台力。

图6是当速度为固定值时，通过编程语言拟合出的动态峰应力随壁厚边长比变化的曲线。

由图6可知动态峰应力与速度的关系曲线形式与二次元方程关系最为接近，则动态峰应力的计算公式为：

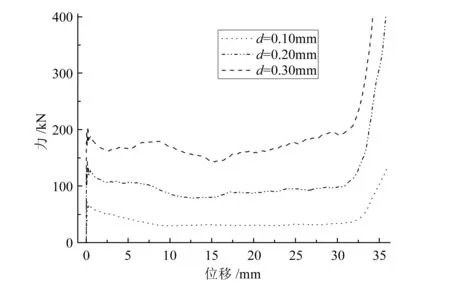
图5 v=90m/s时六边形蜂窝铝3种壁厚 下支反力和压缩位移的关系曲线

图6 不同速度时动态峰应力随壁厚 边长比变化的关系曲线

σ=σyA(d/l)k

(2)

式中：σy为基体材料的屈服极限；k为关系系数。根据最小二乘法可得当速度分别为15，30，50，70，90，110，130，180，250m/s时，动态峰应力与壁厚边长比的关系曲线系数A，k分别为：6.00，1.55；5.62，1.51；5.23，1.46；5.34，1.46；5.20，1.43；5.48，1.42；5.42，1.40；5.26，1.33；4.55，1.20。

2.4 单位体积能量吸收

动态峰应力是六边形蜂窝铝力学性质的主要内容之一，它的大小直接决定蜂窝铝能吸收多少能量。蜂窝铝作为缓冲吸能材料，其单位体积吸能情况是决定其性能好坏的重要指标，只有在具备突出的吸能特性的情况下，才能减少外界撞击给被保护物带来的损失。

当蜂窝铝被压缩到一定程度时，单位体积平台区吸收的能量W可由式(3)求得。

(3)

式中：εd为动能在密实化区达到峰值时的应变；σ(ε)为蜂窝铝被压缩过程中随应变变化的应力。

研究六边形蜂窝铝单位体积吸能情况与速度v和壁厚d的关系时，本文采用与上述相同尺寸的有限元模型。通过整理不同条件下的计算数据，得到应力应变曲线，并经过积分运算得出单位体积能量值，见表2。将表中数据用MATLAB编程语言编辑为单位体积平台阶段能量吸收与速度v和壁厚d的曲线图，如图7、图8所示。

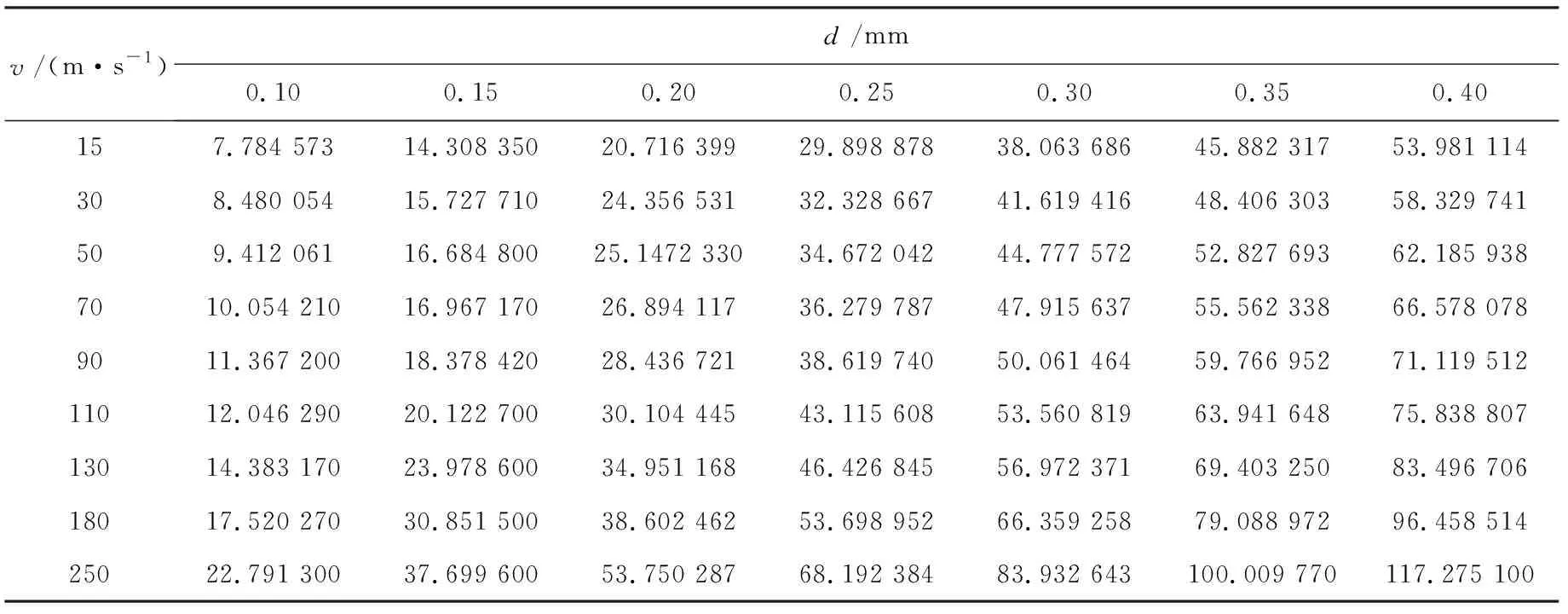
表2 不同壁厚和速度下单位体积平台阶段能量吸收值 kJ

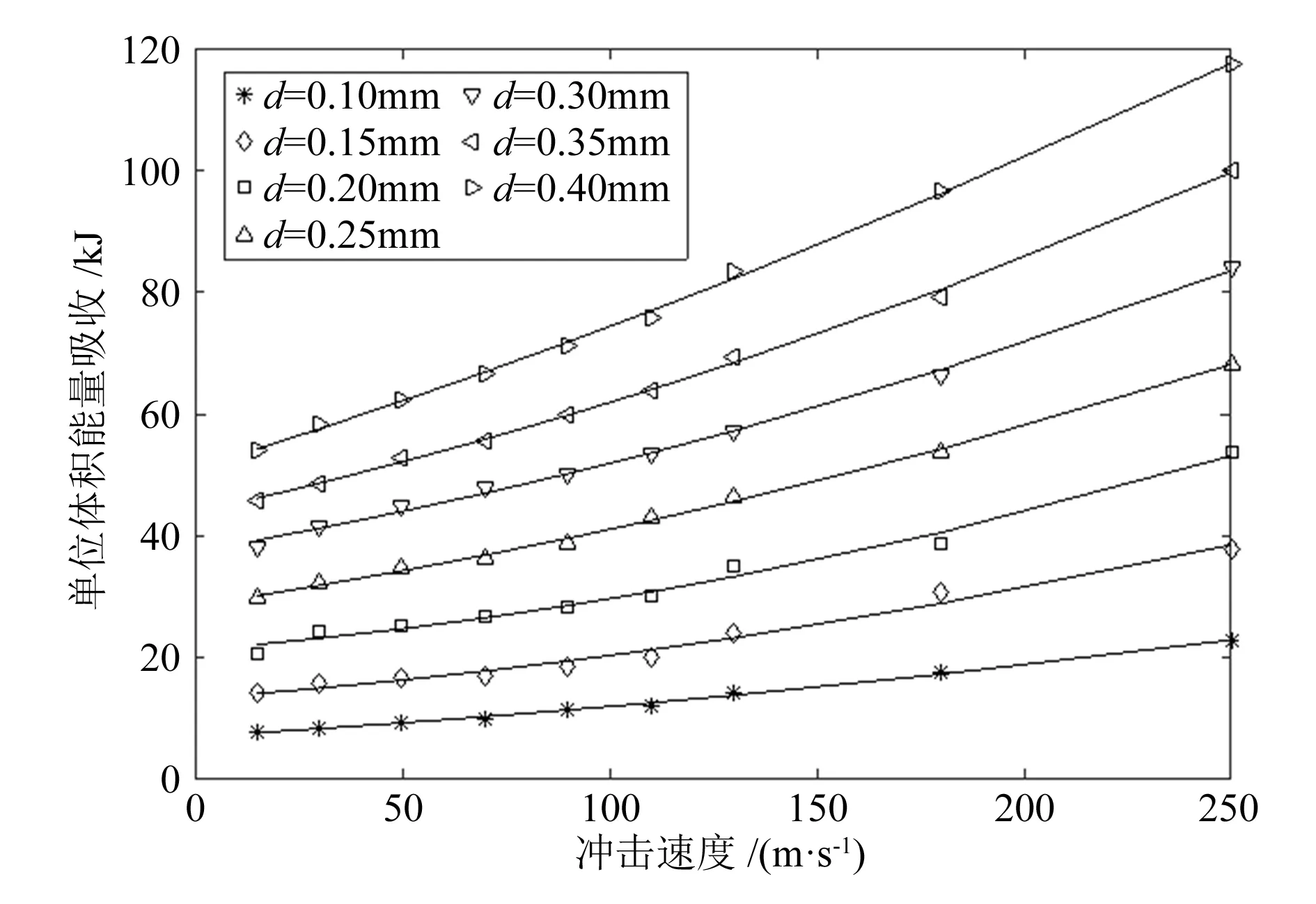
图7 不同壁厚下平台区单位体积 能量值随速度变化的关系曲线

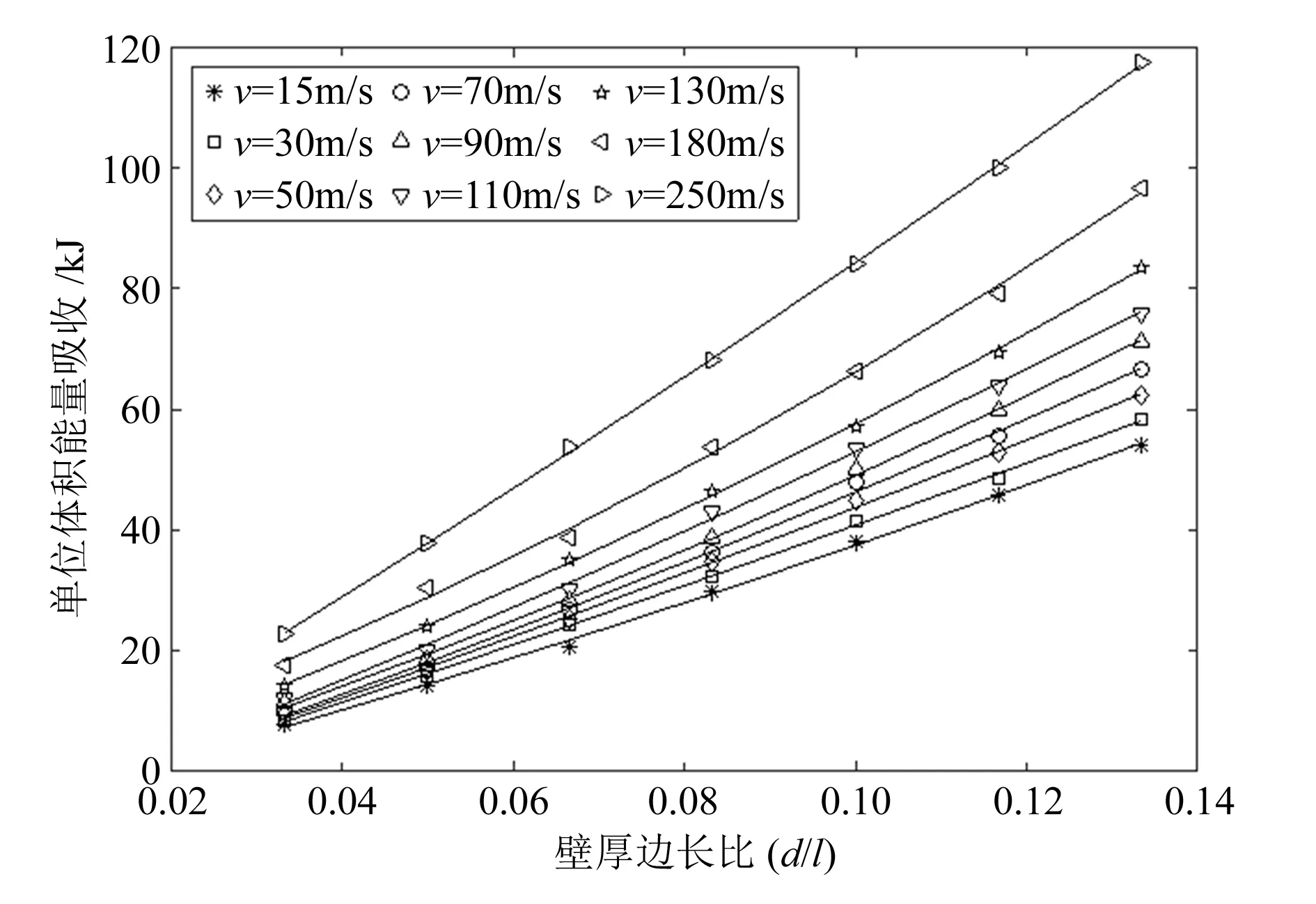
图8 不同速度下平台区单位体积 能量值随壁厚边长比变化的关系曲线

由图可知：单位体积平台阶段能量吸收与速度呈二次函数关系；与壁厚边长比呈幂指数函数关系，与上述动态峰应力仿真曲线结果趋势相近，只是关系系数略有不同。

3 结束语

本文围绕蜂窝铝的异面特性进行仿真模拟，重点研究了速度和壁厚对蜂窝铝动态峰应力和能量吸收的影响。通过大量计算获得数据结果，根据控制变量法用最小二乘法原理拟合出速度和壁厚边长比对动态峰应力和单位体积吸收能量的影响规律，并得出了相关计算公式，为该种类型的材料模型的研究提供了一些理论铺垫。

通过大量模拟仿真研究，可发现影响蜂窝铝吸能的主要因素，通过结构优化和材料改进等措施即可弥补其不足之处，这样做不仅能实现试验的目的，还能大大节省试验费用。正因如此，蜂窝铝作为被广泛使用的缓冲吸能材料，才可在最大程度上发挥出它的优势。