基于损失模型的动车组排障器稳健优化设计

李永华，李会杰，王 剑，高月华

(大连交通大学交通运输工程学院，辽宁 大连 116028)

动车组排障器在清除轨道上一些障碍物时，会受到各方向的强烈撞击，故排障器自身应具有较高的强度，以保证每次在受到不同外界因素干扰时，排障器所承受的应力大小都在安全的范围内，这就要求动车组排障器在静强度方面具有较高的稳健性。

对排障器结构进行稳健优化设计[1]是提高其质量特性的重要手段之一。此方法主要通过调整可控的设计变量和容差大小，使被研究对象对外界影响因素的敏感度降低，从而实现产品的稳健性[2]。目前，大部分学者对排障器的研究重点主要放在对结构静强度、疲劳和碰撞仿真分析的研究上，胡坤镜等[3]通过对200km/h客运机车排障器进行静强度仿真分析，认为纵筋板为其薄弱部位，对纵筋板结构加以优化改进，从而提高客运机车排障器的强度；安治业等[4]对动车组排障器中螺栓的静强度和疲劳进行仿真分析后，以增加螺栓数量、改变连接孔形状等方式，提高了排障器连接安装的可靠性；丁晨等[5]通过对动车组排障器进行碰撞仿真分析，以采用新型吸能结构和填充材料的方式，来提高碰撞安全性。很少有学者从稳健性角度出发，在满足静强度、碰撞等要求的同时，进一步分析排障器结构的稳定性问题。

本文在充分考虑了内外界因素对动车组排障器静强度影响的基础上，提出利用损失模型建立单目标稳健优化模型，利用正交表以及信噪比方差分析得到动车组排障器质量特性的稳健性优化解，并通过蒙特卡洛[6]抽样模拟，确定目标响应稳健性的提高。

1 基于损失模型的稳健优化

1.1 信噪比

损失模型可以转化为信噪比指标来考量产品的特性值[7]。信噪比是用来评测噪声因素对质量特性影响的重要参数，信噪比越大，表示产品的质量水平越高，特性值稳定性越好。信噪比计算公式如下。

望目特性的信噪比：

(1)

望小特性的信噪比：

(2)

望大特性的信噪比：

(3)

式中：y0为质量特性的目标值；yi为质量特性的测量值；N为测量值的个数。

1.2 正交试验和参数设计

正交试验主要利用正交表技术，合理地安排试验设计，从许多试验条件中选出有代表性的少数几项进行试验，获得可靠的试验结果[8]，减少试验组合的次数，以降低随机误差的影响，从而获得较为精确的数据，并提高产品的质量。

模型参数和试验结果参数的设计主要利用正交试验表进行参数组合，并结合信噪比对结果进行方差分析，以得到设计参数的最佳组合。

参数设计的流程如图1所示。

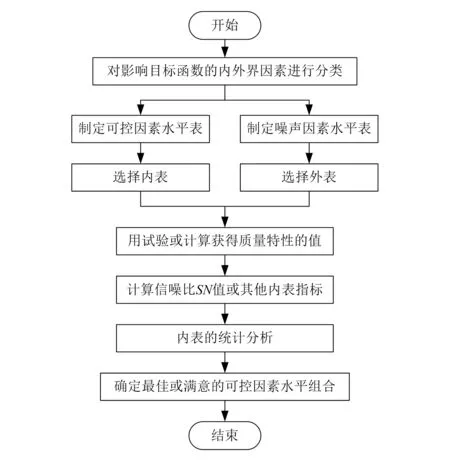
图1 参数设计流程图

2 实例分析

2.1 动车组排障器有限元模型

利用HyperMesh对排障器进行有限元建模，整体采用任意四节点和三节点的壳单元网格进行划分，螺栓连接采用Beam188单元模拟。模型有65 661个单元，64 980个节点，如图2所示。

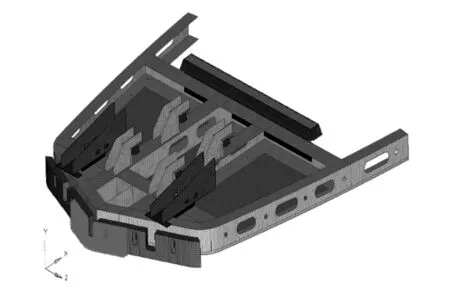
图2 动车组排障器有限元模型

依据铁路车辆标准EN12663:2010，动车组排障器前端面(0.5m宽范围)必须能承受137kN的压缩静载荷，在图2所示的有限元模型中，137kN的载荷力被平均分配到相应的节点上。同时在排障器的尾部和支架的螺栓连接椭圆孔处施加横向、纵向和垂向的线位移约束来最大真实化地模拟排障器在实际工作中的约束状态。

2.2 损失模型

2.2.1试验参数设计

根据设计要求，结合造成排障器应力大小变化的内外界影响因素，选取组成排障器型材板件7种不同的厚度参数A,B,C,D,E,F,G作为控制因素，每个因素对应3个不同水平，见表1；对于噪声因素，外界冲击载荷的大小以及外载荷的方向(与排障器纵向中心轴横向夹角的大小)会对质量特性值产生影响，故选取外载荷F和载荷角θ为噪声因素，每个因素对应2水平，见表2。

表1 控制因素水平表 mm

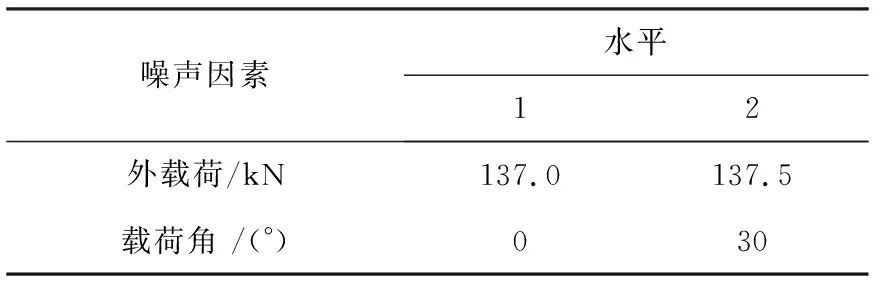
表2 误差因素水平表

根据因素和水平的不同，选取对应的常用正交表。本文的控制变量为7因素3水平，可选取L18(21×37)作为内表，安排可控因素的第一列用来考查试验误差[9]，用参数e表示。由于噪声因子属于2因素2水平，对其可进行全排列组合后作为外表。将外表和内表组合起来，得到动车组排障器应力试验数据表。因排障器所受应力值越小越好，故信噪比应符合望小特性。根据式(2)得出信噪比，如图3所示。

2.2.2试验结果分析

试验因素试验次序列号可控因素11234567eABCDEFG试验次序123412121122噪声因素Fθ信噪比111111111310.20312.39312.39310.20-49.86211222222204.84206.29206.29204.84-46.26311333333165.34166.51166.51165.34-44.40412112233310.18312.37312.37310.18-49.86512223311204.81206.26206.26204.81-46.26612331122166.72167.90167.90166.72-44.47723121323310.14312.34312.34310.14-49.86823232131205.45206.91206.91205.46-46.29923313212166.15167.33167.33166.15-44.441021133221310.18312.37312.37310.18-49.861121211332204.73206.18206.18204.73-46.251221322113166.00167.17167.17166.00-44.431332123132310.31312.50312.50310.31-49.871432231213204.88206.33206.33204.88-46.261532312321165.33166.50166.50165.33-44.401633132312310.17312.37312.37310.17-49.861733213123205.04206.48206.48205.04-46.271833321231166.32167.50167.50166.32-44.45

图3 动车组排障器应力正交试验数据表

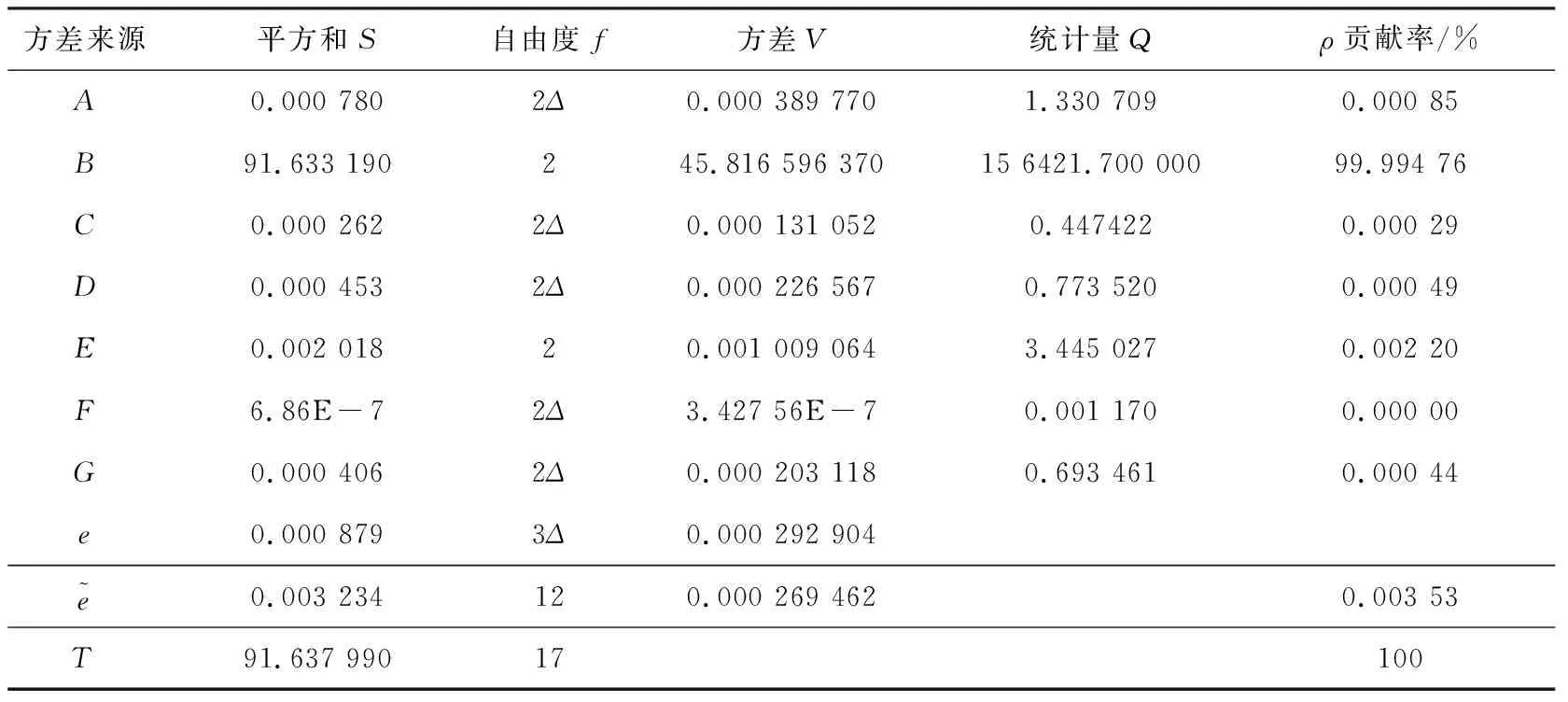
表3 动车组排障器应力大小信噪比方差分析表

方差分析结果表明，由于因素B的统计量QB≫Q122(0.01),贡献率为99.994 76%，故因素B对信噪比的影响(即对输出特性波动的影响)是非常显著的，而其他影响小的因素原则上水平大小可以任选。为了减轻排障器总质量，应选择水平小相对应的型材板厚，即得出最佳组合为A1B2C1D1E1F1G1(A1=3.0mm；B2=6.0mm；C1=9.0mm；D1=11.0mm；E1=14.0mm；F1=18.0 mm；G1=24.0mm)。

2.2.3优化前后结果对比分析

利用ANSYS软件对最佳型材板厚参数组合成的排障器结构进行有限元分析，得到优化后排障器所受应力大小S、总质量M以及安全系数n。优化前后试验结果见表4。为了更加贴切地体现出应力最大的位置，图4给出了在噪声因素F,θ都为1水平作用下排障器优化前后的von Mises应力云图。

表4 优化前后试验结果对比

图4 排障器优化前后von Mises应力云图

通常需要通过计算被研究对象的均值和均方差来确定排障器应力指标优化后的稳健性是否提高，目前常用的计算方法有解析法、矩阵法和蒙特卡罗法等[10]。蒙特卡罗法能很直观地显示优化结果，故本文选用此方法。利用Isight软件中的蒙特卡罗方法对优化前后的设计变量分别抽样1 000次，各获取1 000个数据样本，并对优化前后的质量特性值进行分析，得到目标响应的样本平均值和均方差，见表5。

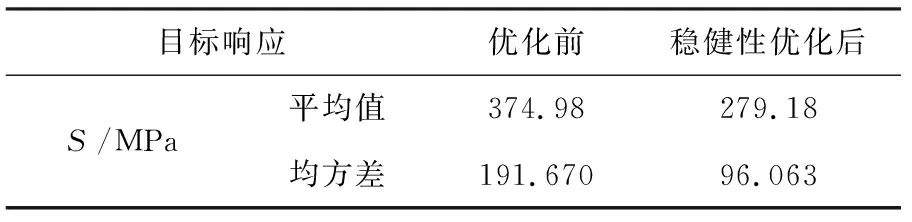
表5 优化前后目标响应的平均值和均方差结果对比

为了更直观地观察目标响应优化前和稳健优化后目标响应的均值和均方差，体现组成排障器的焊接型材板厚参数对目标响应稳健性的影响，图5中分别给出了目标函数优化前后的概率分布直方图。

图5 排障器优化前后目标响应的抽样分布直方图

从表5的数据对比和图5的概率分布直方图可以得知，稳健优化后目标响应的平均值和均方差都有所减小，稳健性有所提高。

3 结论

本文利用损失模型对动车组排障器的结构进行稳健性优化设计，结果表明，5mm厚度的排障器板材对外界载荷作用力是最敏感的，故在容差范围内，将其厚度设置为6mm，使排障器对外力的敏感度降低，应力由217.214MPa降低到173.240MPa，优化率达到20.15%；考虑到其他可控因素的不敏感性，在容差范围内减小型材板件厚度，使动车组排障器的质量由173.97kg减小到161.17kg，优化率为7.53%；随着排障器所受应力的降低，安全系数也由1.21提高到1.51，优化率为24.79%。

通过抽样模拟可知，动车组排障器的应力平均值由374.98MPa降低到279.18MPa，样本的均方差由191.760MPa降低到96.063MPa，故其稳健性有所提高。排障器型材板厚参数合理的组合，不仅提高了动车组排障器结构性能的稳健性和安全性，还一定程度上减轻了其质量。本文的优化设计为动车组其他由型材组成的结构进行稳健优化设计提供了可借鉴的经验，具有较强的工程实用性。