显微组织对Ti-3Al-4.5V-5Mo钛合金拉伸变形行为的影响

李兴无,沙爱学,陈 勃,储俊鹏

（中国航发北京航空材料研究院，北京 100095）

很多重要的工程材料为延性两相合金，如αβ钛合金、双相钢、镍基高温合金等。这类合金具有强度、塑性和断裂韧度的良好匹配，在航空航天等诸多领域中获得广泛应用。从Tamura等[1]提出的改进混合物模型算起，对延性两相合金的变形力学研究迄今已近50年，期间相继出现等应变模型、应变分配模型和应力分配模型[2-5]等，各种模型的主要不同点在于如何假定两个相中的应变分配或应力分配，以及一相的存在如何影响另一相的流变特性。由于延性两相合金材料众多，各种材料显微组织和变形特性都复杂，因此目前尚无统一的变形理论。

Ti-3Al-4.5V-5Mo 为马氏体型 α-β 两相合金[6]，其 β 稳定系数 Kβ≈ 0.8，接近临界浓度（Kβ= 1），同远离临界浓度的合金相比，如α合金和β合金，其晶粒明显减小，在退火状态基本无β转变组织，在钛合金中是较为理想的延性两相合金。因此，可以更好利用现有的延性两相合金变形力学的理论模型理解和表征该合金的变形行为。根据Fan等提出的3-E模型[7-8]，已经研究了Ti-3Al-4.5V-5Mo钛合金的拉伸变形过程中的应力跌落、加工硬化与加工软化等问题[9]。本工作以此为基础，研究晶粒尺寸、晶体取向对Ti-3Al-4.5V-5Mo钛合金拉伸变形行为的影响。

1 实验材料及方法

实验用料为西北有色金属研究院提供的同一炉次的两批ϕ8 mm热轧态丝材（以下分别用Ⅰ、Ⅱ表示），合金化学成分见表1，两批丝材退火后的丝织构存在差异。通过金相法和X射线衍射分析法测定该合金的相转变温度为870 ℃。热轧丝材分别经 720 ℃、780 ℃、840 ℃ 和 880 ℃ 保温 60 min后炉冷退火。

取退火丝材的横向试样，经粗磨、细磨和抛光，制备成织构分析试样。织构分析在X′PERT型X射线仪上进行。测试丝材α相（）、（0002）、（）、（）、（）和（）不完全极图。在此基础上，以Bunge系统计算恒φ2截面ODF，并反算出α相（）、（0002）全极图，分析丝材的织构特征[10]。SEM分析在JSM-5800型扫描电镜上进行，采用图像分割法估算α相和β相的体积分数，采用等效直径法对β相晶粒尺寸进行表征。

经退火后的丝材加工成 ϕ6 mm × 70 mm 的试样，其中工作部分直径为3 mm，标距为30 mm。拉伸实验在Instron-4507型万能试验机上进行，拉伸速率为 1 mm/min，测定 σs、σb、δ、φ、应力-应变曲线，并计算真应力-真应变曲线。其中：真应力σ=P/A，工程应力S=P/A0，真应变ε= ln(L/L0)，工程应变e= (L-L0)/L0，真应变和工程应变的关系为ε=ln(1 ＋e)。

表1 Ti-3Al-4.5V-5Mo 合金的化学成分（质量分数/%）Table 1 Chemical composition of 8.0 mm diameter wire of Ti-3Al-4.5V-5Mo alloy （mass fraction/%）

2 实验结果

2.1 ϕ8 mm 丝材的显微组织

Ⅰ号丝材在不同温度退火炉冷的显微组织如图1所示，随着退火温度的提高，初生α相的形态也逐渐由条状α和球状α的混合组织向球状组织过渡，颗粒尺寸逐渐增加。当退火温度达到880 ℃时，转变成粗晶片状组织。两相区退火后形成α相体积分数约为50%。值得注意的是，由于Ⅰ号丝材经840 ℃退火后β晶粒尺寸有的已经达到5 μm左右，在退火加热后的炉冷过程中在原始β晶粒内已经析出了 α 相，见图 1（c）。和文献 [9]ϕ8 mm 丝材（以下用Ⅲ号表示）相比，显微组织类型类似，但Ⅰ号丝材在两相区退火的晶粒尺寸比Ⅲ号丝材的粗大（见图2），经780 ℃退火后，Ⅰ号丝材β晶粒等效直径约为1.1 μm，而Ⅲ号丝材β晶粒等效直径约为0.7 μm。Ⅱ号丝材和Ⅰ号丝材在840 ℃退火后的α、β晶粒尺寸基本相当。

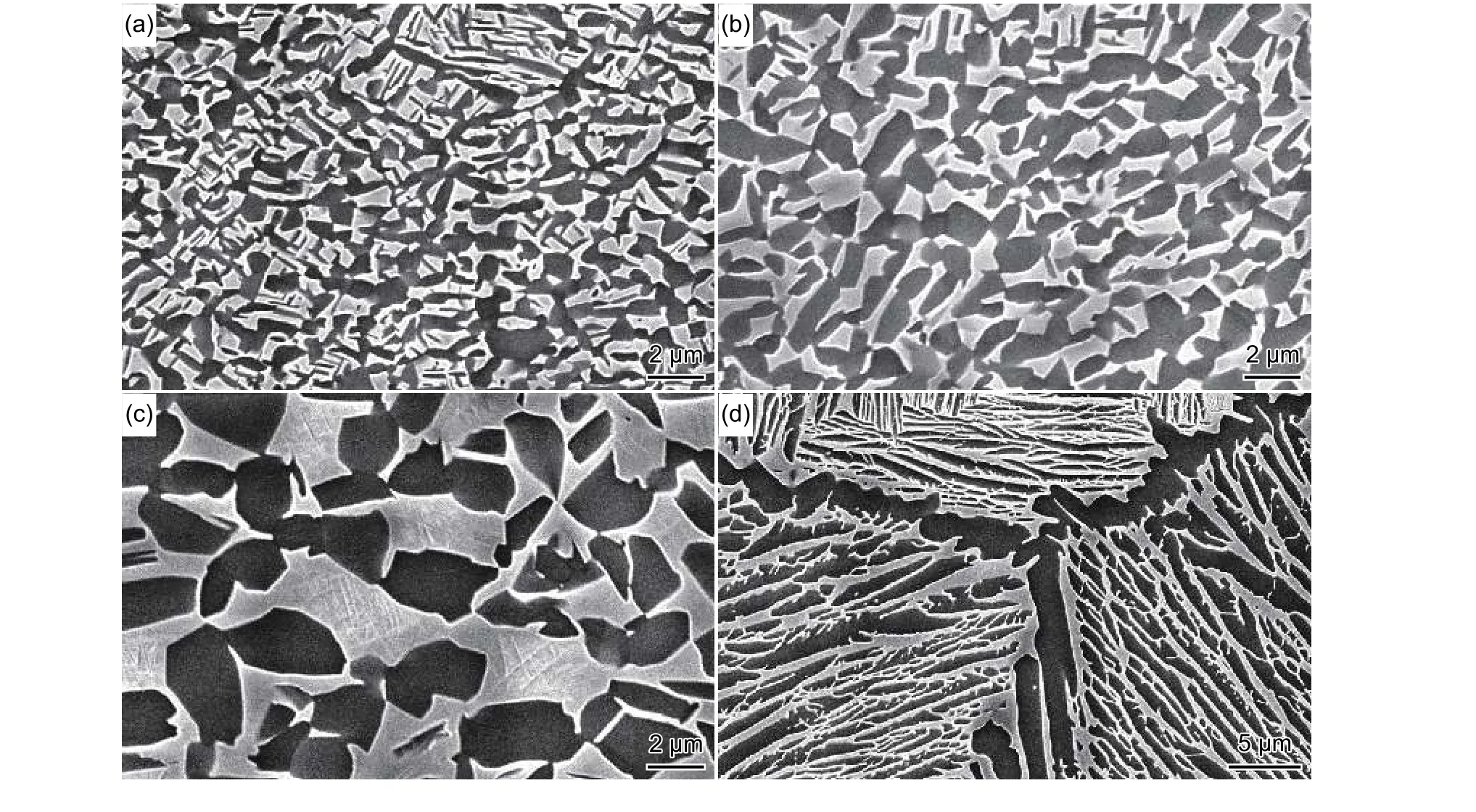
图1 不同退火温度下Ⅰ号丝材的显微组织Fig.1 Microstructures of wireⅠannealed at different temperatures （a）720 ℃；（b）780 ℃；（c）840 ℃；（d）880 ℃

图2 不同退火温度下Ⅲ号丝材的显微组织[9]Fig.2 Microstructures of wire Ⅲ annealed at different temperatures[9]（a）780 ℃；（b）840 ℃

2.2 ϕ8 mm 丝材的晶体取向

Ⅰ号丝材经720 ℃和840 ℃退火后，测在丝材横截面上α相(0002)，()不全极图（经归一化处理），见图 3（a）、（b）和 4（a）、（b）。由图 4 可见，α相(0002)极点密度最大值均出现在丝材轴线。恒 φ2截面 ODF 图（图 2（c）、（d）和 3（c）、（d））显示 α 相的主要织构组分为（φ1，0°，0°）、（φ1，0°，30°）、 （ φ1，0°，0°） 、 （ φ1，0°，30°） ，表 示 α相(0002)平行于试样表面。这表明，α相呈现出较强的<0001>丝织构特征，与Ⅲ号丝材中α相织构特征基本相同。β相基本为<100>丝织构。

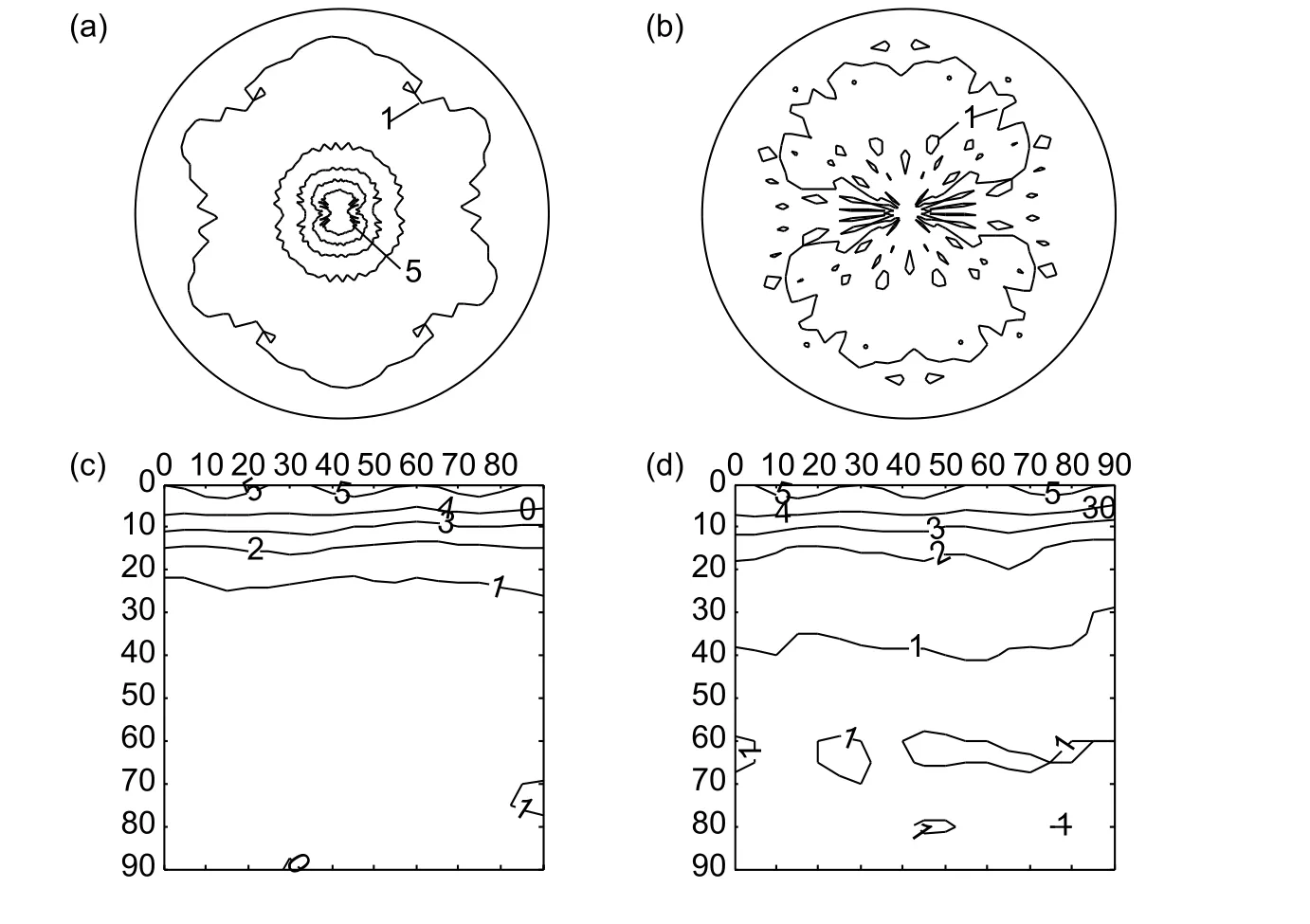
图3 Ⅰ号丝材经 720 ℃ 退火后的 α 相织构 （a）横截面（0002）极图；（b）横截面（ 1 01¯0）极图；（c）φ2 = 0°截面 ODF；（d）φ2 = 30°截面 ODFFig.3 Texture of α phase in wire Ⅰannealed at 720 ℃ （a）（0002）pole figure；（b）（ 1 01¯0) pole figure;（c）φ2 = 0° section of α ODF; （d）φ2 = 30° section of α ODF

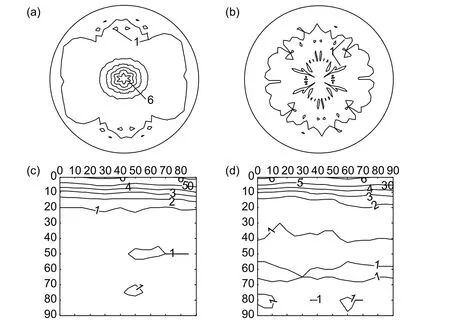
图4 Ⅰ号丝材经 840℃ 退火后的 α 相织构 （a）横截面（0002）极图；（b）横截面（）极图；（c）φ2 = 0°截面 ODF；（d）φ2 = 30°截面 ODFFig.4 Texture of α phase in wireⅠannealed at 840℃ （a）（0002） pole figure；（b）（ 1 01¯0） pole figure; （c）φ2 = 0° section of α ODF; （d）φ2 = 30° section of α ODF

图5和图6为Ⅱ号丝材720 ℃和840 ℃退火后α 相 (0002)、(1 01¯0)不完全极图和恒 φ2截面 ODF图。由图5可知，Ⅱ号丝材主要织构组分为（φ1，90°，30°），这表示 α 相的(1 0 1¯0)面垂直于丝材轴线方向，为<1 01¯0>丝织构；另外，还存在强度较弱的织构组 分 （ φ1，0°，0°） 、 （ φ1，0°，30°） ， 表 示 α 相 的(0001)面垂直于丝材轴线方向，为<0001>丝织构。

2.3 ϕ8 mm 丝材的拉伸真应力-真应变曲线

图7和图8分别为Ⅰ号、Ⅱ号丝材经720 ℃、780 ℃、840 ℃ 和880 ℃ 退火后的拉伸真应力-真应变曲线，和Ⅲ号丝材拉伸真应力-真应变曲线特征类似：拉伸变形过程分为三个阶段（见图9），在720~840 ℃范围内退火产生等轴α相时，均存在屈服后的应力跌落现象，而880 ℃退火无屈服后的应力跌落。

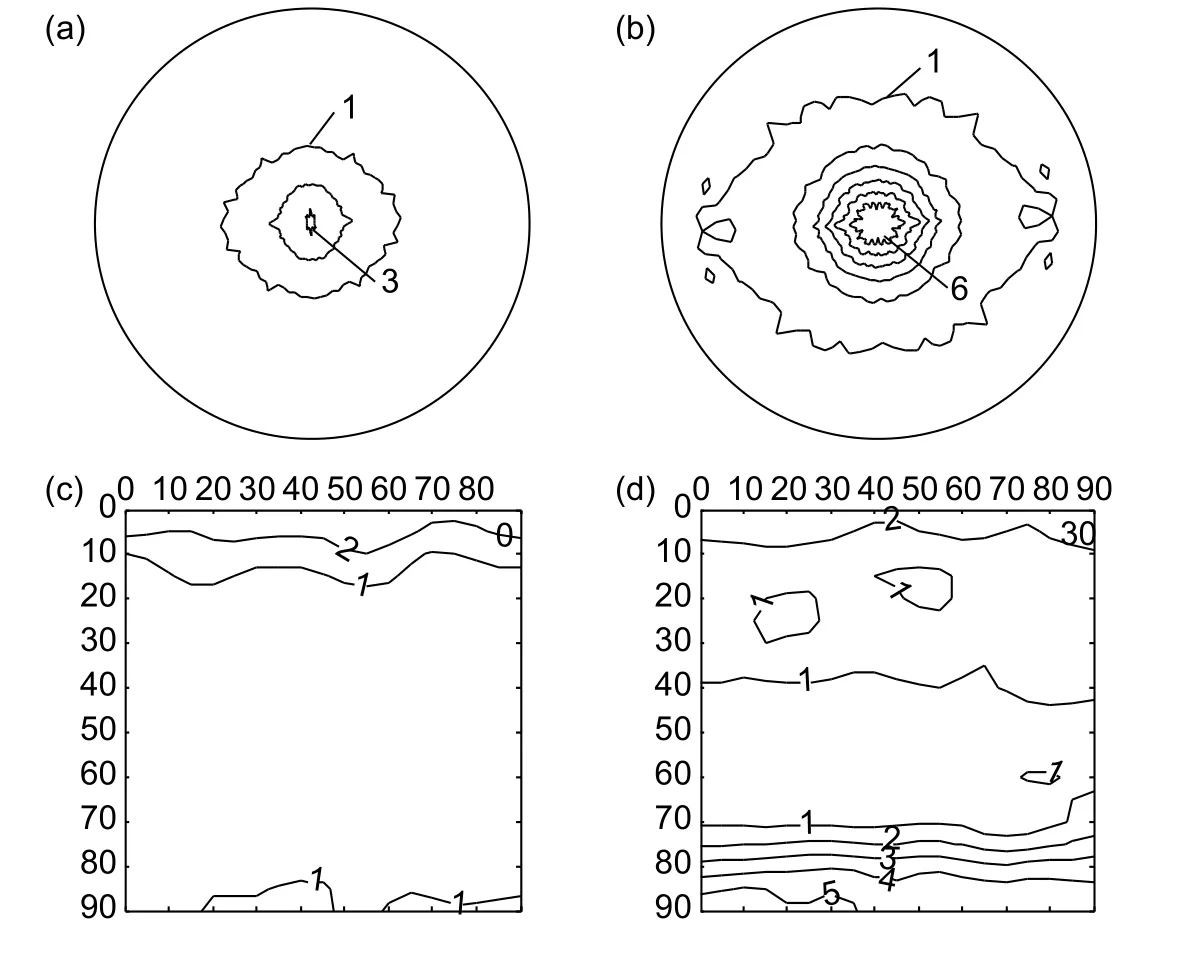
图5 Ⅱ号丝材经 720 ℃ 退火后的 α 相织构 （a） 横截面（0002）极图；（b）横截面（ 1 01¯0）极图；（c） φ2 = 0°截面 ODF；（d） φ2 = 30°截面 ODFFig.5 Texture of α phase in wire Ⅱannealed at 720 ℃ （a）（0002） pole figure；（b）（1 01¯0） pole figure; （c） φ2 = 0° section of α ODF;（d） φ2 = 30° section of α ODF

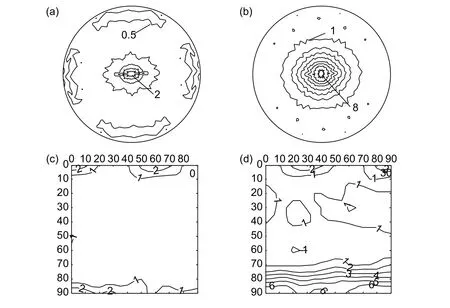
图6 Ⅱ号丝材经 840 ℃ 退火后的 α 相织构 （a）横截面（0002）极图；（b）横截面（）极图；（c） φ2 = 0°截面 ODF；（d） φ2 = 30°截面 ODFFig.6 Texture of α phase in wireⅡannealed at 840 ℃ （a）（0002） pole figure；（b） （）pole figure; （c） φ2 = 0° section of α ODF; （d） φ2 = 30° section of α ODF

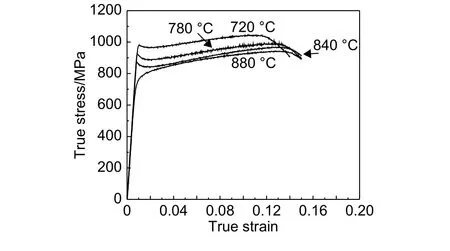
图7 Ⅰ号丝材不同退火温度下的真应力-真应变曲线Fig.7 True stress-true strain tensile curves of wireⅠannealed at different temperatures

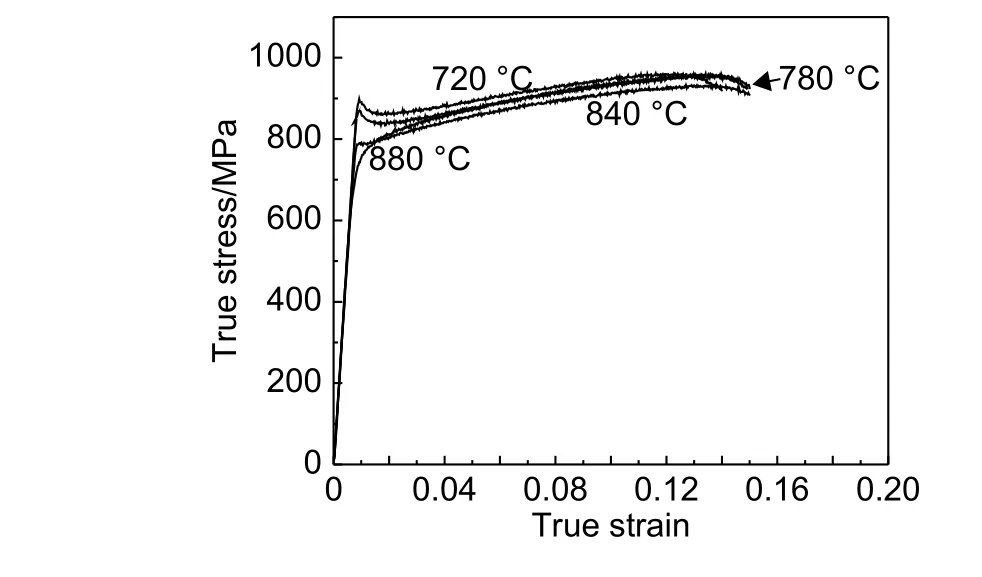
图8 Ⅱ号丝材不同退火温度下的真应力-真应变曲线Fig.8 True stress-true strain tensile curves of wireⅡannealed at different temperatures

3 分析与讨论

3.1 应力跌落及流变应力

两批丝材的拉伸实验验证了Ti-3Al-4.5V-5Mo合金在退火状态下拉伸变形存在应力跌落的规律。当拉伸变形过程进入第②阶段（见图9），α相开始塑性变形，而β相继续保持弹性变形。第②阶段的流变应力可表达为[7-9]：

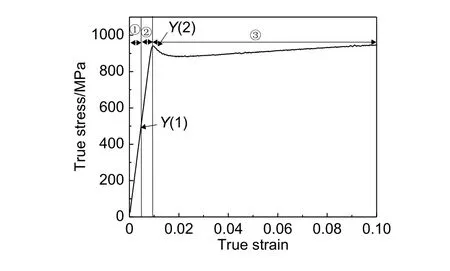
图9 Ti-3Al-4.5V-5Mo 合金在拉伸变形过程的三个阶段[9]Fig.9 Three stages in the process of tensile deformation of Ti-3Al-4.5V-5Mo alloy[9]

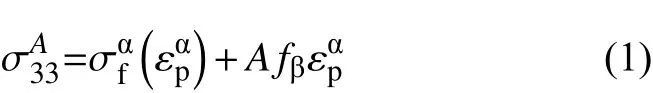
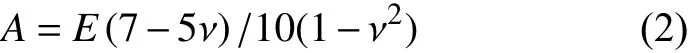
式中：E为弹性模量；ν为泊松比。

在整个拉伸变形第②阶段，β相的塑性变形为零，因此在α相和β相中存在非常大的塑性应变不匹配，根据Eshelby连续体转变理论[11-12]，这在α相和β相中能产生大的内应力。α相中的内应力以弹性能的形式储存在α相中(图9中Y(1)为α相发生塑性变形的临界应力，表达式参见文献[9])，当塑性变形达到β相发生塑性变形的临界应力Y(2)时，β相开始塑性变形，Y(2)可表达为：

式中：fα为α相的体积分数；为β相的屈服强度。

当β相开始塑性变形时，在α相和β相之间的塑性应变不匹配突然降低，储存在α相中的弹性能显著释放，导致流变应力的跌落。另外，β相中的塑性变形量不再为零，两相间的塑性应变不匹配减小，第③阶段加工硬化率也显著降低。第③阶段的流变应力可表达为：

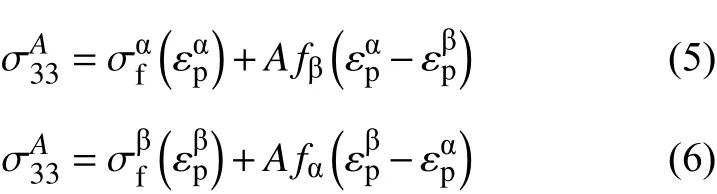
880 ℃退火的片层组织试样，在拉伸时没有出现屈服后的应力跌落。和840 ℃退火所得到的等轴组织相比，在880 ℃退火的片层组织中，α相和β相具有共格界面，滑移更容易从α相传递到β相中，因此，在片层组织中，α相和β相之间屈服强度的差值降低，并导致在第②阶段变形过程中两相间的应变不匹配减小。当β相开始塑性变形时，在α相中没有足够的弹性能释放，在应力-应变曲线上也就没有明显的应力跌落。因此，α相的球化导致α/β两相界面的不共格关系，是产生屈服后应力跌落的必要条件。

3.2 晶粒尺寸对拉伸变形行为的影响

如前所述，Ⅰ号丝材和Ⅲ号丝材，在不同退火温度下的晶体取向基本一致，α相均呈现出较强的<0001>丝织构特征；在不同退火温度下的显微组织类似，但晶粒尺寸存在差异，Ⅰ号丝材在两相区退火的晶粒尺寸比Ⅲ号丝材的粗大。因此，晶粒尺寸的变化是导致Ⅰ号丝材和Ⅲ号丝材拉伸变形行为的差异的重要原因，主要表现在以下两个方面。

一是Ⅰ号丝材不同退火温度下的宏观屈服强度Y(2)Ⅰ均低于Ⅲ号丝材相应退火温度下的屈服强度Y(2)Ⅲ，见图10所示。

根据式（4），Ⅰ号丝材和Ⅲ号丝材可表达为：

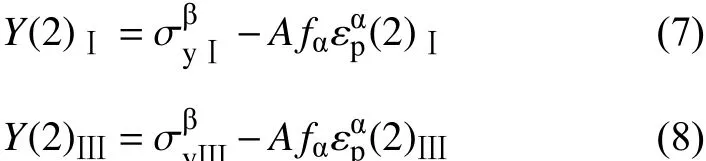
根据Tomota模型[13]，总的塑性应变在α、β相中的分配符合线性混合物模型，即当外加应力达到丝材宏观屈服强度Y(2)时，为零，

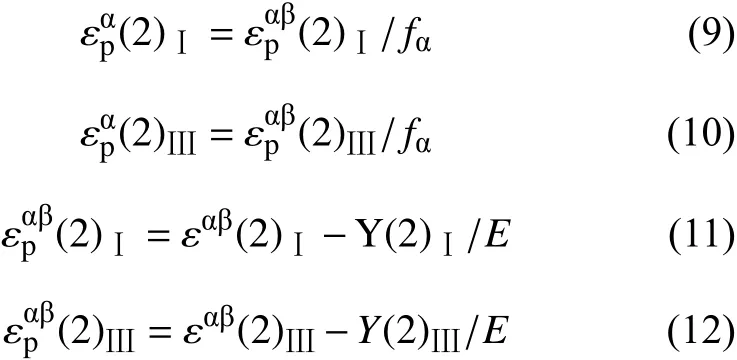
由式（7）~（12）可得：

取 E = 110 GPa，ν = 1/3[8]，K = 0.37 MN/m3/2[14]，fα= 0.5，dⅠ= 1.1 μm，dⅢ= 0.7 μm，780 ℃ 退火时(2)Ⅰ= 0.0092，(2)Ⅲ= 0.0098，得 Y(2)Ⅰ–Y(2)Ⅲ=–99 MPa，和实测数据差值–59 MPa 较为接近，即：

二是在屈服应力跌落后的应力-应变曲线走向存在较大差异。由于Ⅰ号丝材在两相区退火后的晶粒尺寸较大，α相和β相均存在较大的加工硬化系数，导致不论在两相区高温退火，还是在两相区低温退火，在应力-应变曲线上均表现为屈服后加工硬化。

3.3 晶体取向对拉伸变形行为的影响

Ⅰ号丝材α相主要为<0001>丝织构，而Ⅱ号丝材α相主要为<>丝织构。两批丝材经840 ℃退火后，α相晶粒尺寸相当，因此可排除晶粒尺寸因素影响，分析丝材织构对合金拉伸屈服强度的影响。由图1可见，840 ℃退火后的β相中已有α相析出，可称之为β转变组织。由于β转变组织中的α相和β相具有共格关系，为简化处理，可视β转变组织为一个相，记为β′。两批丝材840 ℃退火后的真应力-真应变曲线如图11所示，Ⅰ号丝材的宏观屈服强度明显高于Ⅱ号丝材，即 Y(2)Ⅰ> Y(2)Ⅱ，可见α相晶体取向的差异对丝材拉伸变形行为产生重要影响。

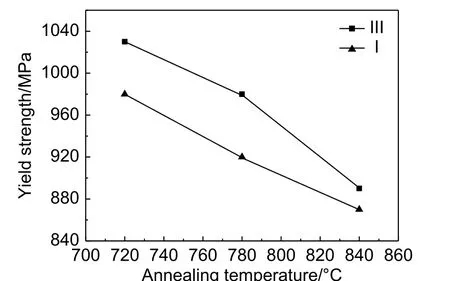
图10 不同温度退火下丝材的屈服强度Fig.10 Yield strength of wires annealed at different temperatures

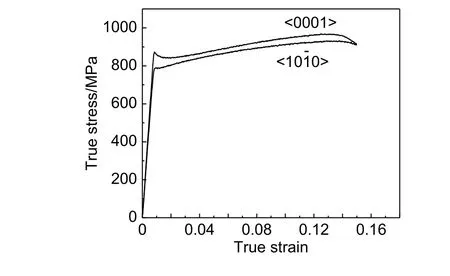
图11 不同 α 相丝织构合金的真应力–真应变曲线Fig.11 True stress-true strain tensile curves of wires with different α phase textures

再由式（19）和（20）可得：

4 结论

（1）不同状态的Ti-3Al-4.5V-5Mo钛合金丝材拉伸实验结果验证了在720~840 ℃退火后的拉伸真应力-真应变曲线上存在明显的宏观屈服点以及屈服后出现了应力跌落。β相开始塑性变形后储存在α相中的弹性能显著释放时流变应力的跌落的原因。α相的球化产生α/β两相界面的不共格关系，是屈服后应力跌落的必要条件。

（2）当α相晶体取向均为<0001>丝织构特征时，根据细晶强化理论，晶粒尺寸的大小决定合金的宏观屈服强度，晶粒尺寸越大，宏观屈服强度越小。

（3）α 相<1 01¯0>丝织构的存在，将产生基面a滑移、柱面a滑移和锥面a+c滑移，由于锥面a+c滑移的临界分切应力要明显高于基面a滑移和柱面a滑移，对于α相<0001>丝织构，在α相中产生较大的塑性变形，β相中内应力增加，合金宏观屈服强度降低。