无油涡旋压缩机小曲拐动力特性与仿真研究

彭 斌，朱永军

(兰州理工大学机电工程学院，甘肃 兰州 730050)

无油涡旋压缩机作为一款新型的流体机械，具有高效、节能、可靠、免维护的优点。作用在涡旋压缩机动盘上的切向力会使动盘产生绕主轴偏心线转动的自转力矩，使动静盘不能正常啮合[1-2]，进而影响涡旋压缩机的性能，因此大多数无油涡旋压缩机利用小曲拐防自转机构限制其自转，以保证涡旋压缩机能够稳定工作。彭斌等[3]对无油涡旋压缩领域的工作做了详细总结，指出无油涡旋压缩机具有巨大的发展潜力，此外彭斌等[4]还对变截面涡旋压缩机的几何模型和动力学模型进行了详细的阐述；Morishita等[5]对涡旋压缩机几何和动力学模型进行了详细的论述；李超等[6]分析了小曲拐的受力及运动平衡方程，并得出3个小曲拐有较好动力学性能的结论；赵曼等[7]分析了3个小曲拐在不同角度的应力应变状态；李超[8]分析了驱动内嵌式涡旋压缩机动力学模型。

ADAMS软件是具有权威性、应用范围很广的虚拟样机仿真软件，可以利用它对虚拟样机进行静力学、运动学和动力学分析[9]：胡跃华等[10]利用ADAMS软件对涡旋压缩机柔性体进行了分析，指出小曲拐在压缩机启动3s之后趋于稳定；李超等[11]对涡旋压缩机十字滑环及主轴进行了仿真分析。本文从运动学和动力学两个方面分析无油涡旋压缩机小曲拐的受力情况并计算了各个力、力矩与摩擦损失；利用三维软件SolidWorks与ADAMS对涡旋压缩机进行虚拟装配与运动仿真，所得数据可为小曲拐的优化设计提供参考。

1 小曲拐机构与动力特性分析

1.1 小曲拐的机构模型

图1所示为涡旋压缩机小曲拐装配图，图2为小曲拐四杆机构模型，3个小曲拐两端的轴颈分别插在动盘与机架的轴承内，根据机构学与装配难易程度确定3个小曲拐装配简单且能自由运动[4]，并沿圆周均匀分布。其中，O为主轴中心,O1为动盘中心，从装配简图中可以看出小曲拐为一个四杆机构[7]。其机构模型如图2所示，其中1为连接电动机的偏心主轴，2为连接偏心主轴与小曲拐的动 盘，3～5为3个小曲拐，6为机架。机构有5个活动构件，8个旋转副，其中有2个虚约束。虚约束为重复的约束，需要去掉虚约束，由此得到的机构自由度计算公式为：

图1 小曲拐装配简图

F=3n-(2p1+ph)=3×3-(2×4+0)=1

(1)

式中：F为自由度数目；n为小曲拐的数目；p1为低副约束数；Ph为高副约束数。

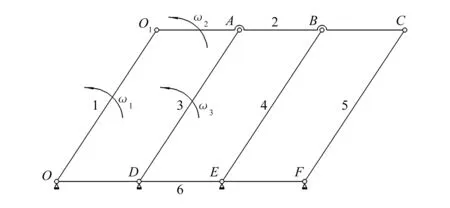
图2 小曲拐四杆机构模型

机构的自由度为1，保证了小曲拐的正常运动。从小曲拐四杆机构可以看出小曲拐的运动与偏心主轴的运动保持一致，使得动盘不发生自转，满足涡旋压缩机防自转的要求。

1.2 小曲拐的受力分析

小曲拐的受力分析如图3所示，(a)为小曲拐主视图，(b)为旋转θ时的左视图。各部分的参数分别为：偏心距e为5.74mm，偏心部分高h1为30mm，中间圆盘高h2为10mm，底部高h3为28mm，偏心部分半径r1为6mm，底部半径r2为8.5mm，中间圆盘半径R为15mm，小曲拐质量m为0.118kg，偏心部分质量mc为0.032kg，小曲拐与动涡盘之间的摩擦系数μ为0.032 4。动涡盘对小曲拐的作用力为Qi，机架对小曲拐的作用力为Q,动涡盘对小曲拐的摩擦力为f1，机架对小曲拐的摩擦力为f2，摩擦力产生的力矩为M1，小曲拐受到的力矩为M2。

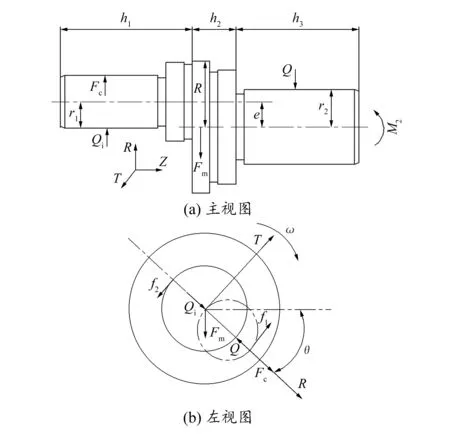
图3 小曲拐受力分析

根据功能平衡关系可得动盘对小曲拐的作用力Qi为[8]：

(2)

式中：Ft为动盘受到的切向力；Ror为偏心距；RoQ为动盘中心到小曲拐的偏心距离；θ为小曲拐偏心部分转动过的角度。

根据受力分析建立小曲拐的力和力矩的平衡方程，在受力方向R方向上，由∑FR=0得：

Fc+Qi-Q+Fmsinθ=0

(3)

由Z方向力矩为0，即∑MZ=0得：

M1+f1(r1+e)+f2r2=0

(4)

由T方向力矩为0，即∑MT=0得：

(5)

由式(2)～(5)，可得：

Q=Qi+Fc+Fmsinθ

(6)

(7)

小曲拐的摩擦损失功率为：

(8)

式中：n1为转速，取值1 440r/min；Lx为小曲拐摩擦转矩；θ′为小曲拐转动角度。

对式(3)～式(8)利用MATLAB软件进行编程求解。如图4所示，由于动盘公转的作用，在一个周期内小曲拐的受力是连续的，且每个小曲拐在一个周期内两次受力达到峰值，两次受力为0，其周期是2π。由于主轴转角达到4.4π时，切向力达到最大值，故而小曲拐3在此时承受的力大于小曲拐1和2承受的力。

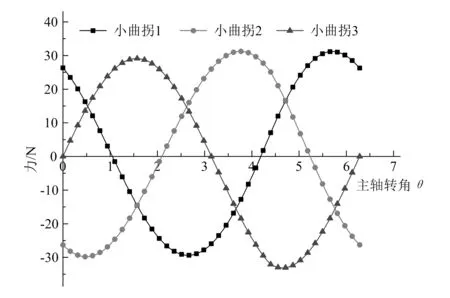
图4 动盘对小曲拐作用力

机架对小曲拐的作用力如图5所示。机架对小曲拐的作用力受动盘对小曲拐的作用力影响，因此其作用力效果和动盘对小曲拐的作用效果相同。

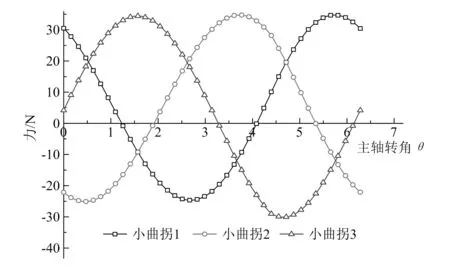
图5 机架对小曲拐作用力

小曲拐受力的正负仅表示受力的方向，因此摩擦损失为正值，小曲拐的摩擦损失如图6所示，其周期与作用力周期相同，也为2π。

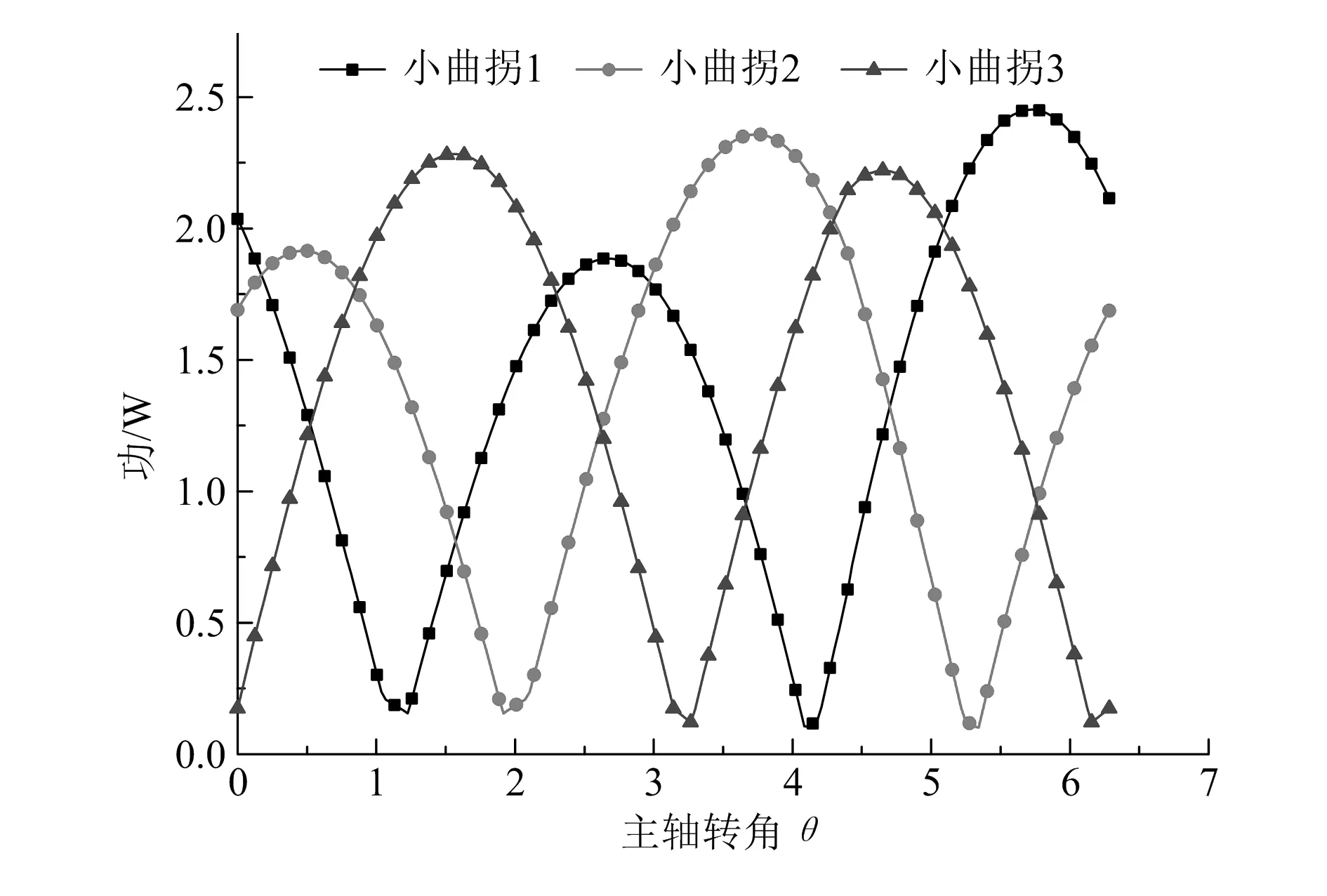
图6 小曲拐的摩擦损失

2 涡旋压缩机虚拟样机的建立

2.1 三维模型的建立

利用三维软件SolidWorks建立涡旋压缩机的三维模型，并转换成通用parasolid格式导入到ADAMS中建立动力学模型。

2.2 虚拟样机的装配

在ADAMS中，根据各零件之间的装配关系进行虚拟样机装配，装配好的样机模型如图7所示。

图7 涡旋压缩机装配图

3 涡旋压缩机的仿真分析

3.1 创建约束

涡旋压缩机的爆炸图如图8所示，从爆炸图中很容易就能看出各个零件之间的连接关系。在虚拟样机装配好之后，对涡旋压缩机各零件之间添加约束关系及驱动，按电机的额定转速设置主轴的转速为1 440r/min。

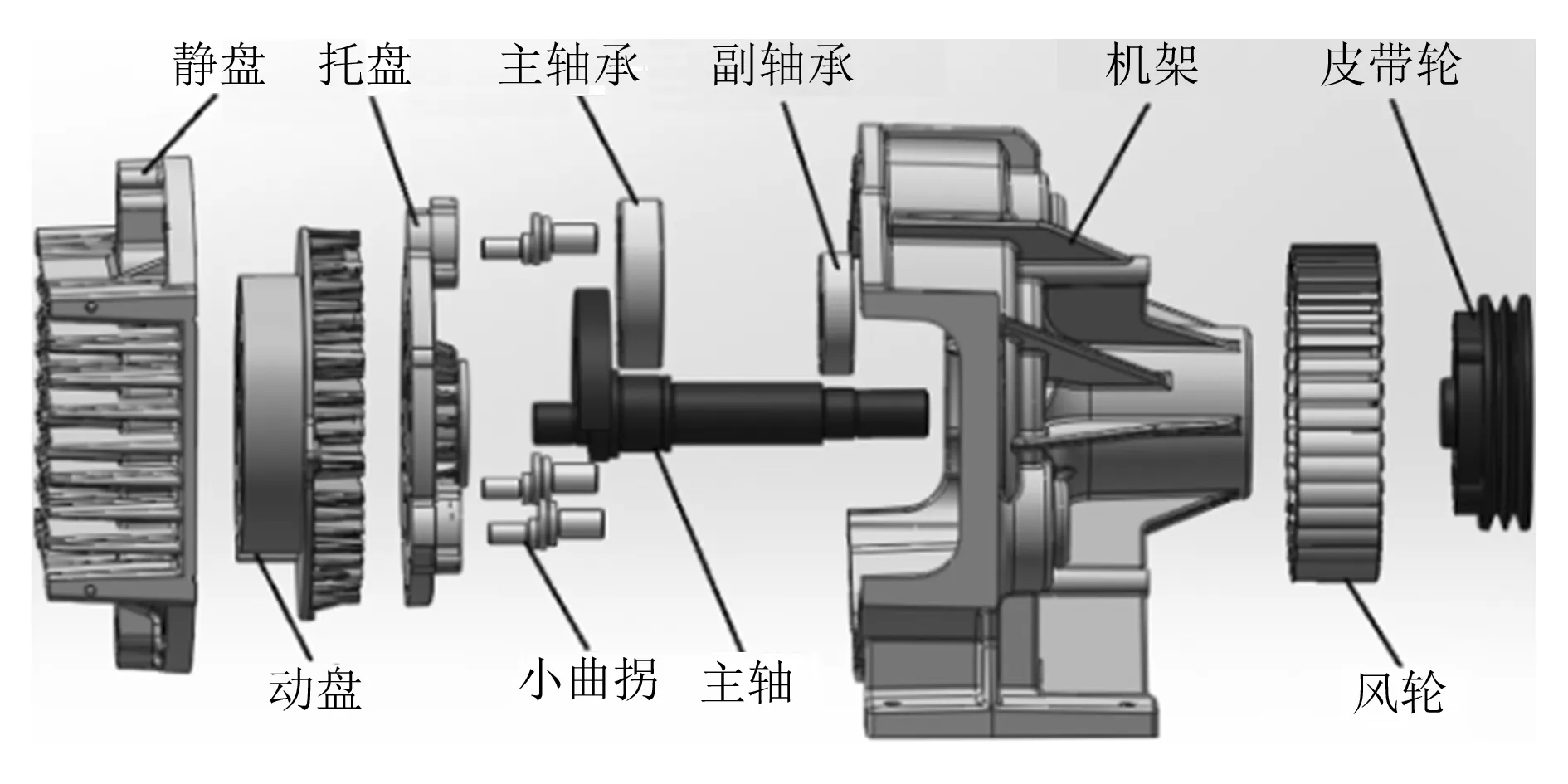
图8 涡旋压缩机爆炸图

各个零件之间的约束见表1[10]。

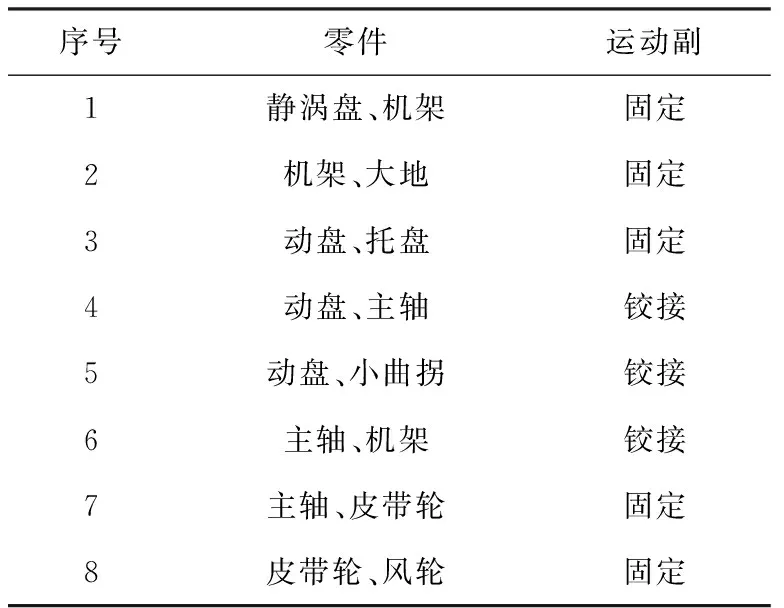
表1 涡旋压缩机各零件约束关系

3.2 小曲拐运动理论与仿真分析

小曲拐的偏心距与主轴的偏心距相等，由小曲拐四杆机构模型可以得出小曲拐与偏心主轴是同步运动的，两者的运动规律相同[6]。小曲拐偏心部分绕小曲拐中心做圆周运动，当转过θ时，小曲拐偏心部分运动方程为[12]：

(rsinθ)2+(rcosθ)2=r2

(9)

式中：r为主轴与小曲拐偏心距。

Sx=rsinθ=rsin(ωt)

(10)

Sy=rcosθ=rcos(ωt)

(11)

式中：Sx为小曲拐x方向的位移；Sy为小曲拐y方向的位移；ω为小曲拐转动角速度；t为小曲拐转动时间。由式(10)、(11)求得小曲拐偏心部分速度：

(12)

(13)

在偏心主轴转动2π过程中，小曲拐偏心部分在x轴、y轴方向上的投影为简谐运动。

偏心主轴与小曲拐具有相同的结构形式，因此偏心主轴与小曲拐具有相同的运动形式。

小曲拐偏心部分与主轴偏心部分的运动轨迹如图9所示，从图中明显看出，两者的运动为圆周运动。

图9 小曲拐与主轴的运动轨迹

由于3个小曲拐的运动规律一样，因此只给出小曲拐1的运动规律。图10、图11所示分别为小曲拐1偏心部分x,y方向的速度与位移曲线，从图中可以看出小曲拐偏心部分x,y方向的运动为简谐运动，说明小曲拐的运动为圆周运动。

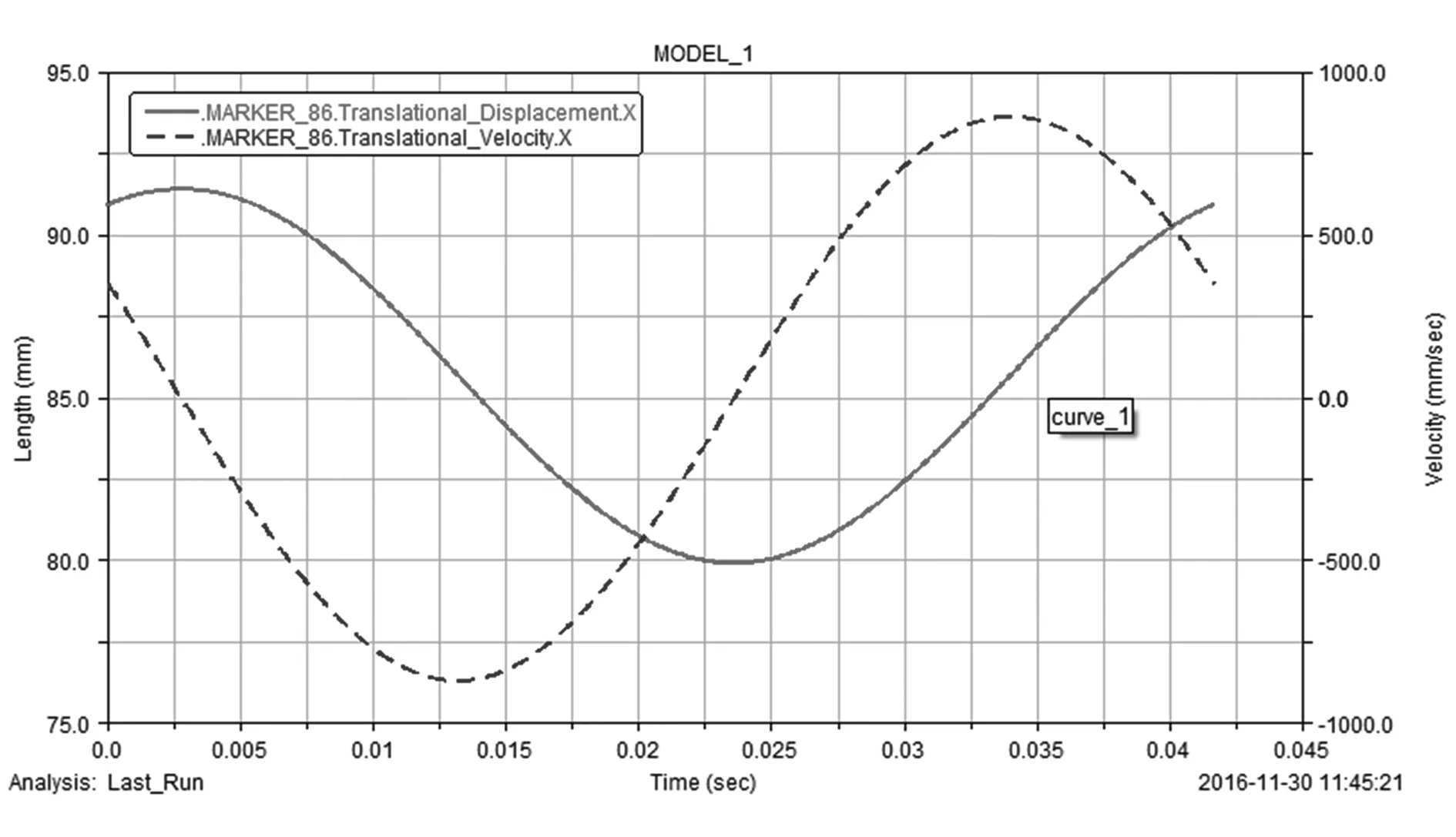
图10 小曲拐1偏心部分x方向速度与位移

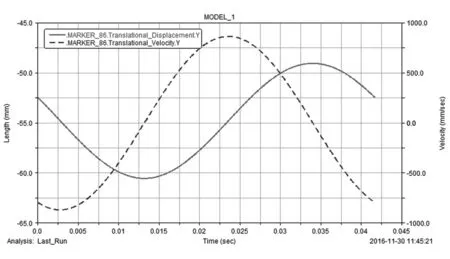
图11 小曲拐1偏心部分y方向速度与位移

图12、图13所示分别为涡旋压缩机主轴偏心部分x,y方向的速度与位移曲线。从图中可以看出主轴偏心部分x,y方向的运动为简谐运动，说明主轴的运动为圆周运动，且主轴的运动规律与小曲拐相同，使得不发生自转，符合小曲拐的平面四杆机构运动规律，从而验证了小曲拐防自转机构的可行性。

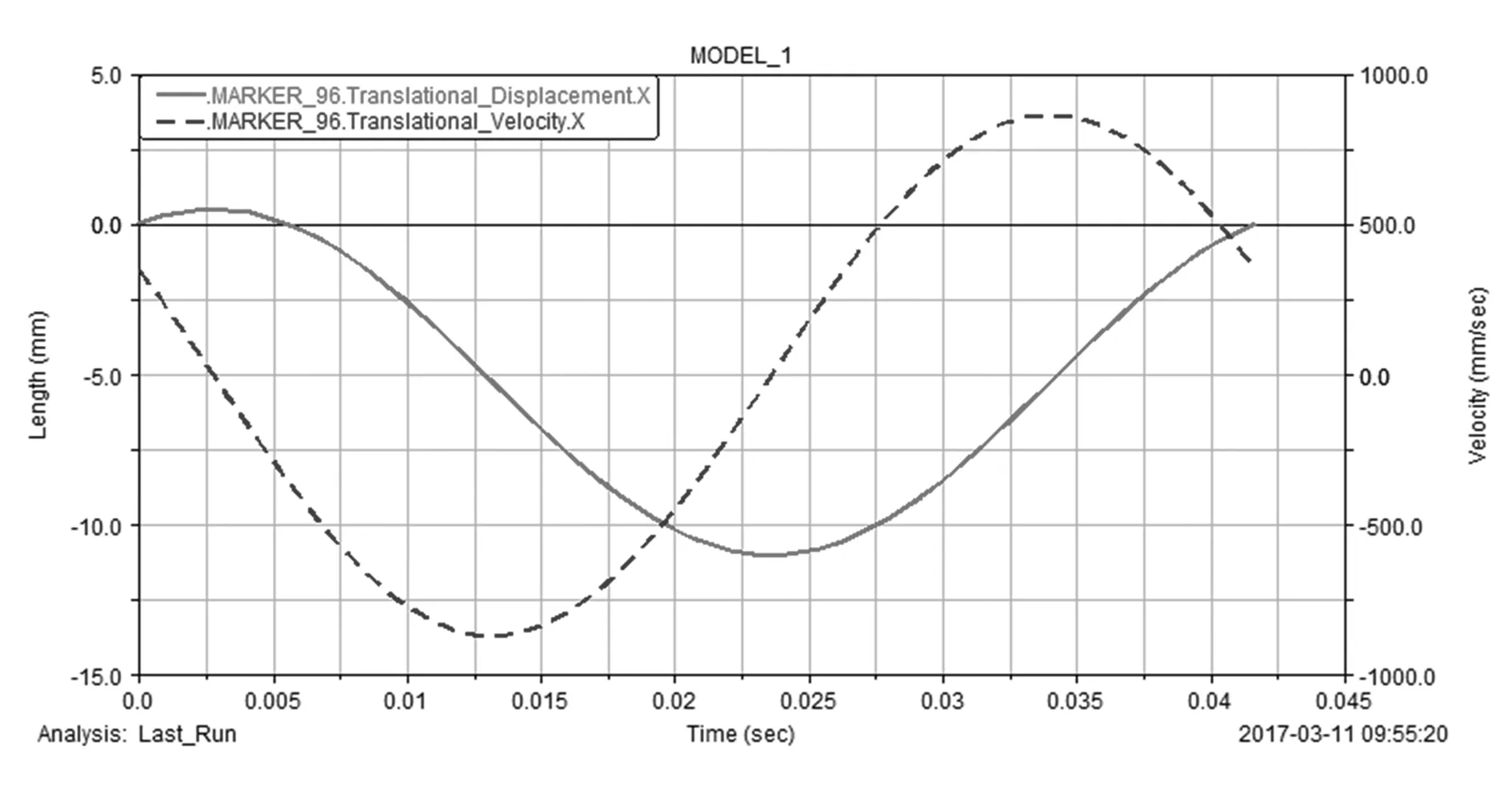
图12 主轴偏心部分x方向速度与位移

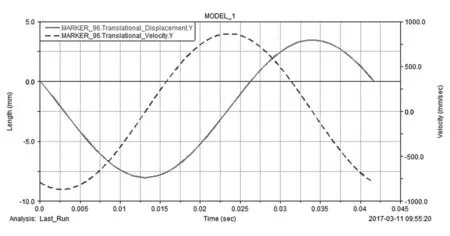
图13 主轴偏心部分y方向速度与位移

4 结束语

本文从机构学入手，同时结合运动学与动力学对涡旋压缩机小曲拐的受力及运动形式进行了综合分析，并通过仿真运动验证了小曲拐防自转结构的可行性，所得结果可为无油涡旋压缩机的结构优化改造提供技术支持。