功能梯度输流管的非线性自由振动分析
2018-08-02朱晨光徐思朋
朱晨光, 徐思朋
(中国海洋大学 工程学院,山东 青岛 266100)
功能梯度材料是由两种或两种以上材料“混合”而成,由此得到的材料组成和力学性质是沿某种方向均匀变化的,简称为FGM(Functionally Graded Materials)。功能梯度材料克服了复合材料在连接界面材料性质突变的缺点,能够更加有效的利用材料,减小残余应力和热应力,也可以作为粘结层连接不同的材料,因而在航空航天、建筑材料、电子、传感器、化学、生物医学乃至日常生活诸领域都得到了广泛的应用[1-4]。在微型管方面,现在已经被应用在原子力显微镜(AFM)上,在共鸣器、制动器、声呐等方面也有很好的应用前景[5]。作为一种非均匀材料,对功能梯度材料的深入研究,有助于进一步推广其工程应用,同时也能促进非均匀材料力学的发展。
目前,关于功能梯度梁的研究已经有很多,其中大部分梁模型假设材料参数沿梁高度按指数型变化。但对于材料参数沿径向变化的功能梯度管的振动研究相对较少。文献[6]考虑尺度效应,将Timoshenko 梁模型用于管,计算了微纳米尺度功能梯度管的非线性振动。但利用Timoshenko梁模型计算管道振动时,由于管内、外表面的剪应力须为零,该光滑状态(friction-free condition)并不容易满足。若采用三维弹性模型,则计算十分复杂。为解决此难题,文献[7]提出了一个适用于管的高阶梁模型,文献[8]则基于该模型分析了功能梯度管的热后屈曲问题。
本文将采用该模型[7]研究功能输流梯度管的非线性振动问题。关于管内流体对管道振动的影响已有较多的研究。如文献[9]应用修正偶应力理论分析了简支微纳米输流管自由振动时流速对自然频率和非线性频率的影响;文献[10]基于该理论,分析了微尺度下悬臂管内流流速对振幅的影响;文献[11]则考虑尺度效应,应用应变梯度理论得出了简支微管内流流速和自然频率的关系,并和欧拉-伯努利梁理论以及修正偶应力理论的结果进行了比较分析;文献[12]讨论了非线性弹性基上输液管在周期振荡流作用下的振动特征;文献[13]研究了输流管道在管内流体及管外海洋荷载共同作用下的涡激振动特征。而关于功能梯度输流管的研究相对较少,文献[14]采用横截面材料性质随半径幂函数变化的功能梯度参数,应用壳模型对功能梯度圆柱壳结构进行了振动分析。依据壳模型得到的结果比较精确,但其方程十分复杂。文献[15-16]采用欧拉梁模型,分别分析了轴向功能梯度输流管与功能梯度输流曲管的振动问题。二者都是采用将欧拉梁控制方程中材料系数加以替换的方式得到的控制方程,且考虑的皆为线性问题。本文采用沿管径方向变化的功能梯度参数,基于一个适用于管的高阶梁模型并应用哈密顿原理,得出了管道振动的控制方程。然后,利用Galerkin方法对方程进行了离散化。最后,采用多尺度法得到了功能梯度输流管非线性振动时自然频率和非线性频率的表达式。
多尺度方法是一种有效的解决弱非线性问题的近似计算方法。由于它不仅能用来计算周期运动和稳态响应,还能够被用于计算耗散系统的衰减振动以及非稳态过程,所以在非线性振动方面得到了很好的应用(文献[24], 83页)。本文通过文章中耦合方程频率相等的证明,应用多尺度法求得了线性和非线性的频率表达式,应用频率表达式,能够更加方便直观的分析输流管非线性自由振动的特征。
1 功能梯度输流管的控制方程
如图1所示的两端简支的功能梯度管,长为L,内径为Ri,外径为Ro。建立如图所示的两个坐标系,其中yz坐标系为管横截面的坐标系,坐标原点为管截面的中心点,y轴为水平方向,z轴正方向竖直向上;xyz坐标系为整体坐标系,x轴为管的纵向方向;θ为管截面上y轴与z轴夹角逆时针方向的角度,r为管截面上点距截面中心的距离。易知有y=rcosθ,z=rsinθ. 为推导的方便以及表达式的简洁,后文的推导过程主要以xyz坐标系进行,将r,θ视为y,z的函数。为适应圆截面的特点,在数值计算时,则将y,z以r,θ表示进行计算。假设管道由材料1和材料2构成,材料参数沿径向按指数形式变化。管道的材料性质为:
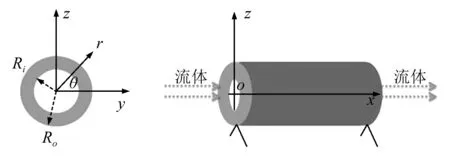
图1 功能梯度输流管模型Fig.1 Model of FG tube conveying fluid
(1)
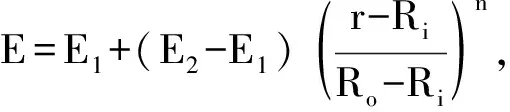
由文献[7]知,适用于管的高阶梁模型位移场方程如下:
U(x,y,z,t)=U0(x,t)+fW0(x,t)′+gφ(x,t)
(2)
W(x,y,z,t)=W0(x,t)
(3)
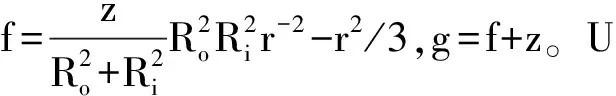
(4)
(5)
(6)
(σxx,τxy,τxz)=(Eεxx,Gγxy,Gγxz)
(7)
式中:εxx、γxy、γxz为相应下标的应变,σxx,τxy,τxz为相应的应力,E为管道材料弹性模量,G为剪切模量。考虑管道受内流作用,运用哈密顿原理:
(8)
式中:Us表示系统的势能,Ks表示系统的动能[17],具体如下:
(9)
(10)
式中:v为管内流体的流速,ρp、ρf分别为管道和流体的密度;Ap、Af分别表示管的截面积以及流体的截面积,流体的截面积即管道内的空心部分截面积。k1,k2分别表示管道和流体的动能,分别为:
将式(4)~(7)代入式(9)~(10),化简后可得功能梯度输流管的控制方程如下:
(11)

(12)
(13)
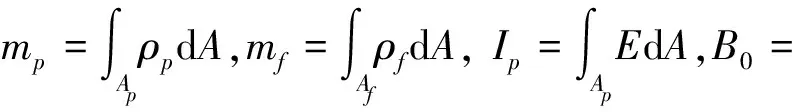
2 多尺度法求解
两端简支的管道,其边界条件为:
x=0,U0=0,W0=0;x=L,U0=0,W0=0
考虑管的自由振动,轴力在管长范围内保持不变[19],即:
(14)
两边对x积分后,代入边界条件,可解得:
(15)
将上式代入控制方程式(12)~(13),并运用Galerkin方法将其进行离散化处理,即设:
(16)
保留系统的一阶阵型[21,26],则利用振型函数的正交性和函数性质,控制方程简化为:
(17)
式中:C1=mp+mf+π2B3/L2,C2=π4Ip/(4L4),C3=π2B0/L2+π4B1/L4-π2mfv2/L2,C4=πB4/L,C5=πB0/L+π3(B1+B7)/L3,G1=πB4/L,G2=πB0/L+π3B2/L3,G3=B9,G4=π2(B2+B8)/L2+B0。ε为表征系统微小改变的无量纲小量。
运用多尺度方法[24]假设:
Φ(t,ε)=Φ0(T0,T1)+εΦ1(T0,T1),
Ψ(t,ε)=Ψ0(T0,T1)+εΨ1(T0,T1)
(18)
式中:Ti=εit(i=0,1),表示不同的时间尺度。将式(19)代入式(17),按ε的同阶次合并同类项,可得:
(19)
(20)
式中:Di(i=0,1)为微分算子符号,表示对Ti求偏导数。具体为:
假设ε0中Ф0的解为[21-22]:
(21)
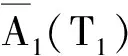
Φ0(T0)=Φ0(T0+2π/ω)
(22)
Ψ0=F(Φ0)=F(Φ0(T0+2π/ω))=
Ψ0(T0+2π/ω)
(23)
则Ψ0为周期函数,假设Ψ0最小正周期T′,则:
T′≤2π/ω
(24)
2π/ω≤T′
(25)
由式(24)、(25)可得2π/ω=T′,则可以假设方程组ε0的解为:
(26)
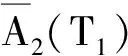
ω=-[(C12G42-2C1C3G3G4-2C1C4G2G4-2C1C5G1G4+
C42G22-2C4C5G1G2+C52G12)1/2-C1G4-C3G3+C4G2+
C5G1]/(2C1G3-2C4G1)
(27)
将解代入式(20)的右边,利用多尺度法的可解性条件,可得功能梯度输流管的非线性频率:
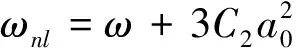
(28)
式中:a0为假定管道按照一阶振型振动时,管道L/2处的初始振幅。
3 算例和讨论
在本文中,除另有提及,均假设Ri=0.8Ro,L=40Ro。管的材料,选择由铝和环氧树脂组成的功能梯度材料。其中材料1铝的主要参数为:弹性模量E1=70 GPa,密度ρp1=2 700 kg/m3,泊松比v1=0.23。材料2环氧树脂主要参数为:弹性模量E2=1.44 GPa,密度ρp2=1 200 kg/m3,泊松比v2=0.38[19],流体密度为ρf=1 000 kg/m3。当n=0时,管道为单一材料的环氧树脂管道。
本文使用MATLAB软件来进行相关的数值计算工作。考虑到本文的材料参数(式(1)),都是与截面上点与截面中心的距离r有关,其关系为幂指数关系;且本文的主要系数,都是材料参数的相应函数在管截面上积分而得,故而在功能梯度参数n较大时,计算量将十分巨大。本文采用均匀分层的方法计算所需的各个系数,即将管道截面分为均匀厚度的多个部分,每层视为均匀的材料,每层的材料性质取当层的中间值,最后将所有层的数值加和,视为整个截面的积分值,即本文所需的系数。在n=0时,计算量较小,可以直接积分计算。均匀分层法结果与直接积分法结果在n=0时的比较发现,当分层数足够大时(本文分层数为100,系数误差都在10-6以内),均匀分层法是十分有效的。所得数值结果及其相关讨论如下文。
在退化状态下(n=0),本文所得单一材料输流管道的线性与非线性频率如图2~5所示。由图可见,本文所得结果与其他理论符合的很好,这在一方面也验证了本文方法的正确性。同时,从图2~3可以看出,在管长和内外径比值固定的情况下,自然频率随管径的增大而减小,并随流速的增加逐渐接近临界点。这与管径增大时管道的刚度增大相关,而流速的持续增大会使管道振动进入不稳定状态。从图4~5中可以看出,非线性频率和自然频率的比值随管长与外径比值的增大而减小,随振幅的增大而增大;并且随着振幅的增大,频率比增大的速度越来越快。这表示随着初始扰动的增大,会使系统的振动更加不稳定。
对功能梯度输流管,图6给出了材料参数对自然频率的影响。由图可见,随着材料1的比例增大(n的增大),频率升高的很快。这是因为材料1的弹性模量比较大,而弹性模量直接影响到系统的刚度,进而影响系统的自然频率。非线性频率与自然频率的比值也与流体的流速有关系,由图7可见随着流速的增加,比值逐渐增大,且流速越靠近临界流速,这种影响也越大。这反映出随着流速的增大,非线性振动响应增加的很快,管的振动越来越接近不稳定状态。图8为临界流速vc(即输流管道线性频率为0时的流速)与管长、管径之比L/Ro在不同功能梯度参数之下的关系。由图可见,输流管的临界流速随功能梯度参数的增大而增大,这从图6中也可以看出。另外,临界流速受L/Ro的影响很大,且随着L/Ro的减小,临界流速增加的越来越快。L/Ro反映了管道的长细比大小,说明在管道的长细比变大时,管道的临界流速会减小,即更容易失稳。
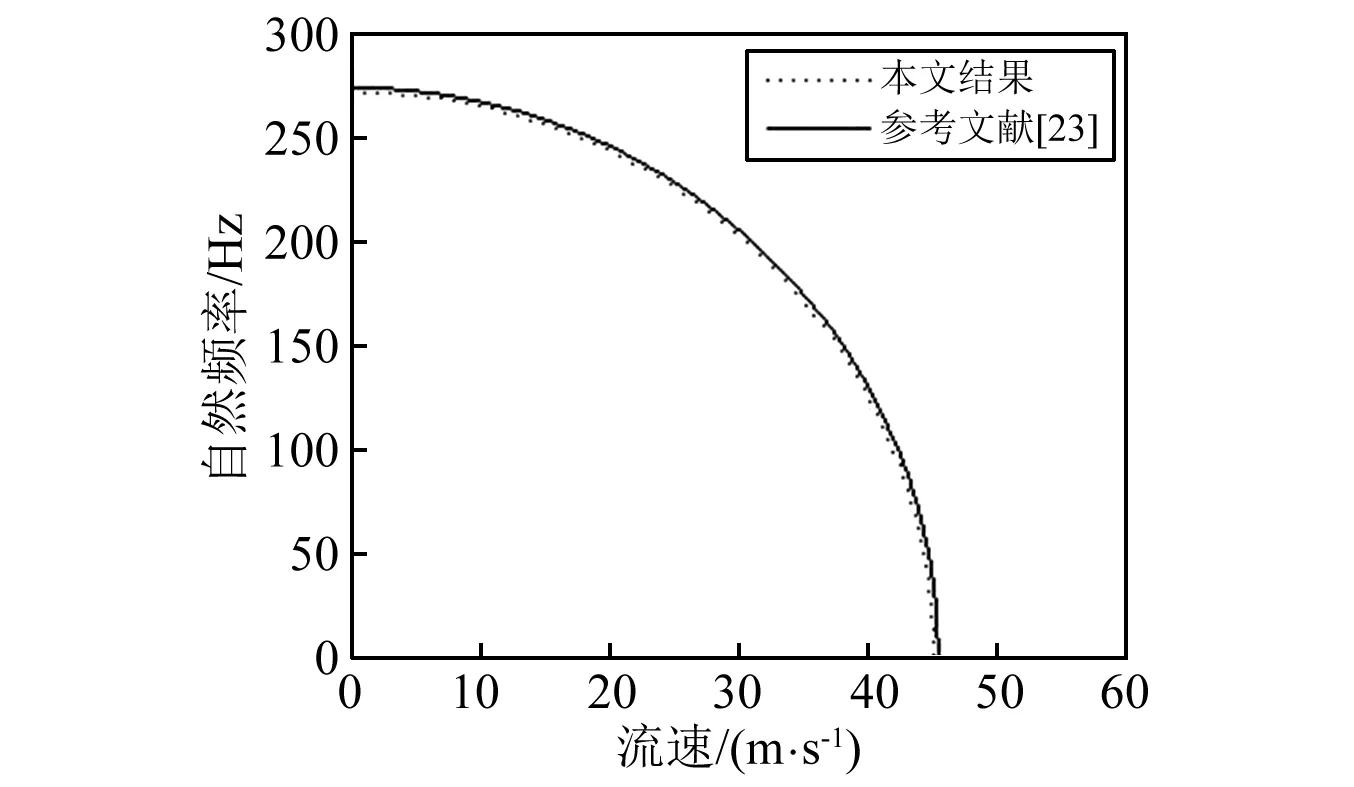
图2 自然频率与流速的关系,其中n=0, Ro=1 cmFig. 2 The relationship between nature frequency and inner fluid velocity for n=0, Ro=1 cm.
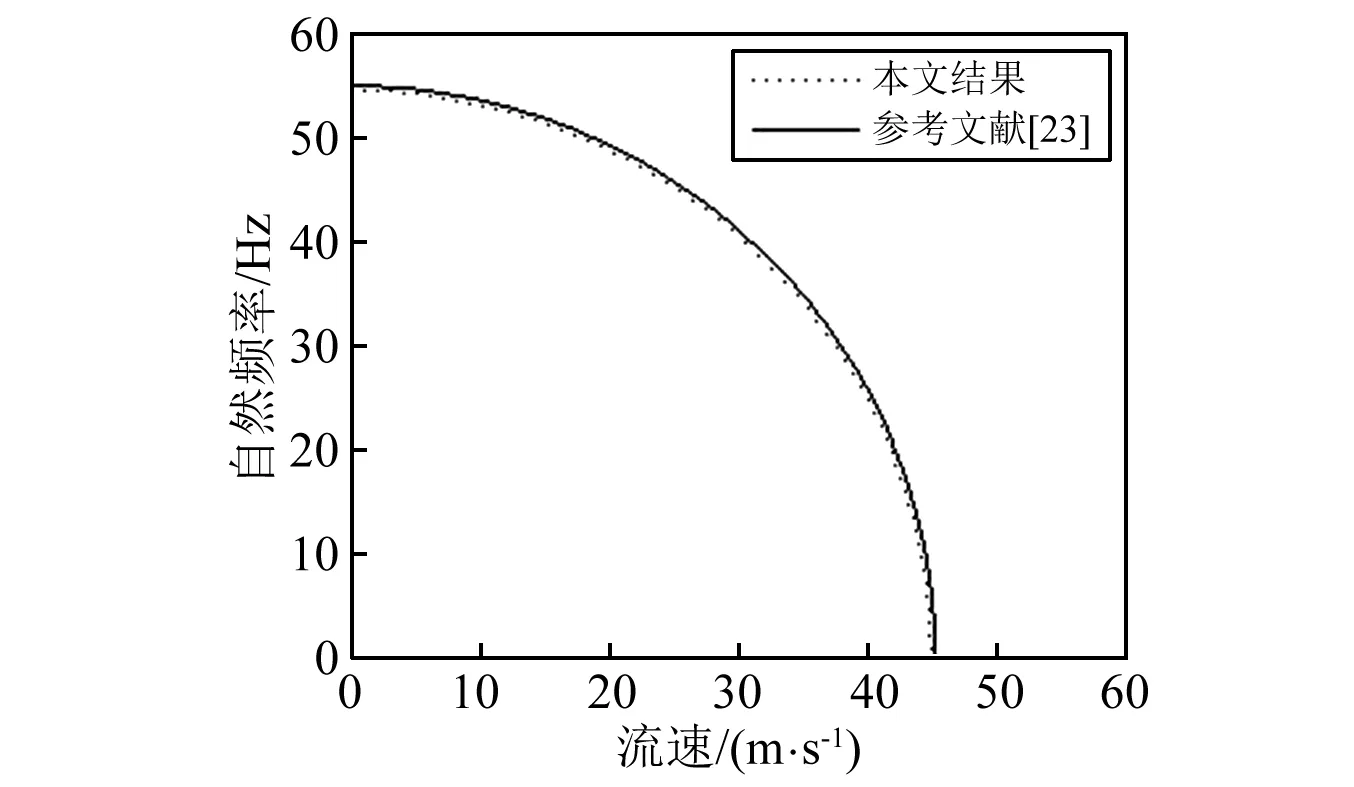
图3 自然频率与流速的关系,其中n=0, Ro=5cmFig.3 The relationship between nature frequency and inner fluid velocity for n=0, Ro=5 cm
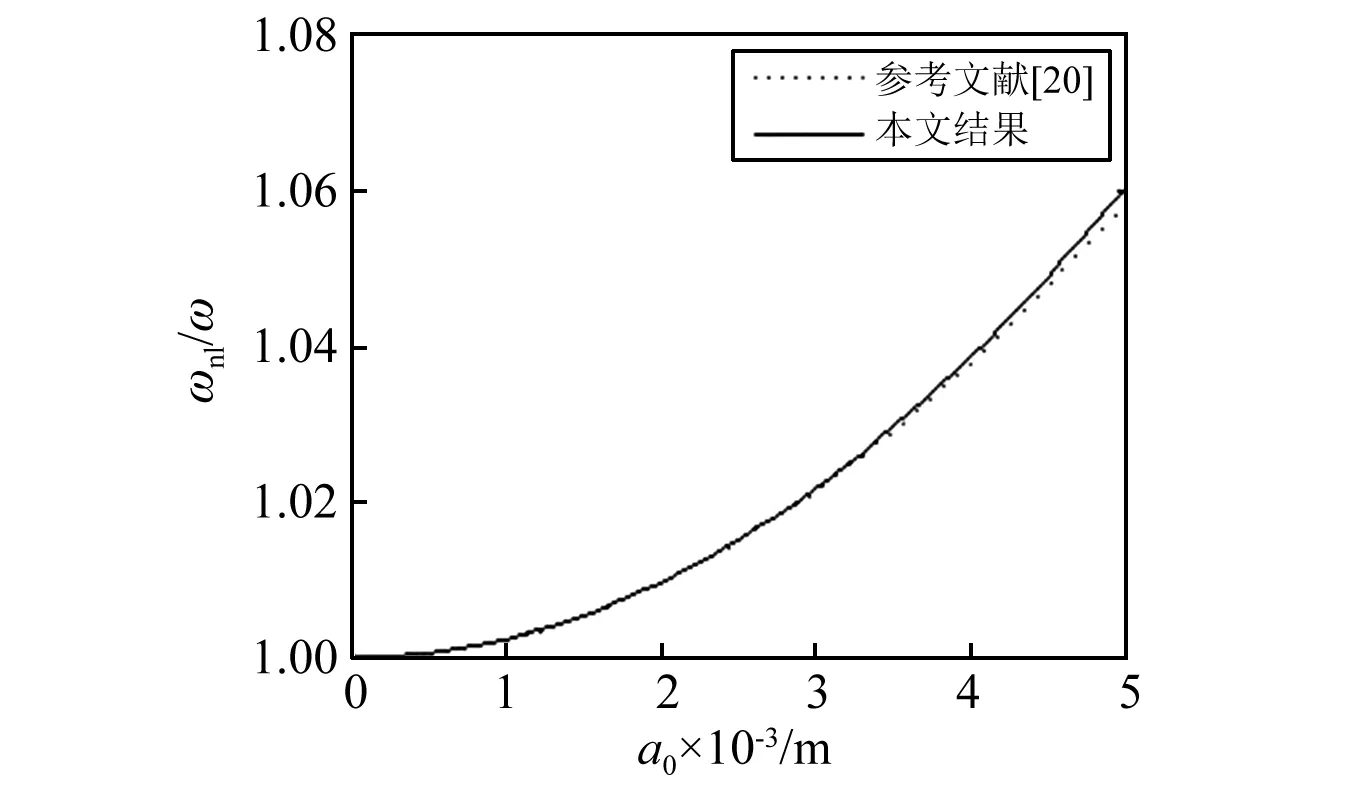
图4 非线性频率和自然频率的比值与振幅的关系,其中n=0, Ro=1 cm, ρf=0, L=20RoFig.4 The relationship between ratio of nonlinear frequency to nature frequency and amplitude for n=0, Ro=1 cm, ρf=0, L=20Ro
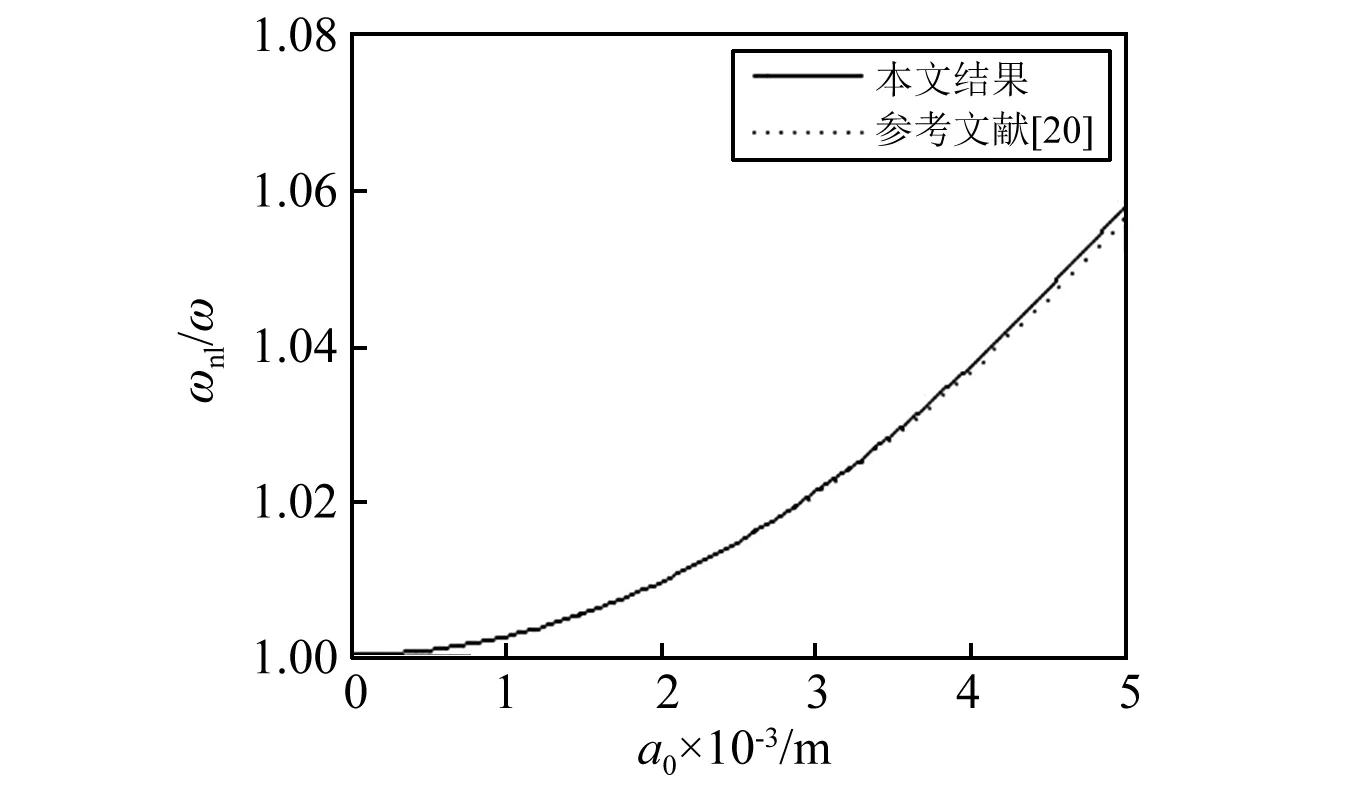
图5 非线性频率和自然频率的比值与振幅的关系,其中n=0, Ro=1 cm, ρf=0, L=40RoFig.5 The relationship between ratio of nonlinear frequency tonature frequency and amplitude for n=0, Ro=1 cm,ρf=0, L=40Ro
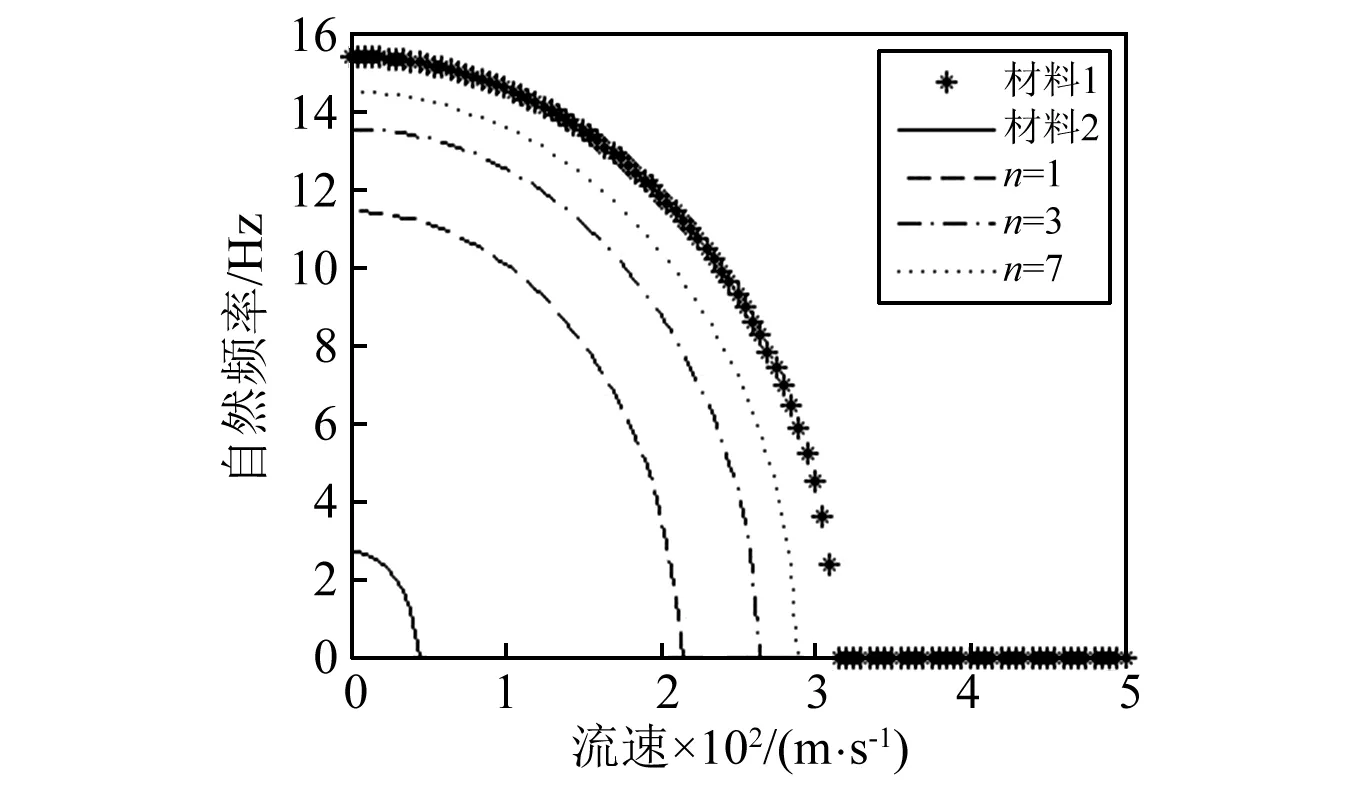
图6 不同功能梯度参数下,自然频率和流速的关系,其中Ro=1 cmFig.6 The relationship between nature frequency and fluid velocity under different FG parameters for Ro=1 cm
功能梯度管道非线性频率与自然频率比值和管道功能梯度参数n的关系见图9~11,图9~11具体材料工况见表1。除弹性模量外,材料1、材料2其他材料属性(密度、泊松比)皆保持不变。

图7 不同流速下,非线性频率和自然频率比值与振幅的关系,其中Ro=1 cm, n=0Fig.7 The relationship between ratio of nonlinear frequency to nature frequency and amplitude under different velocities for Ro=1 cm, n=0
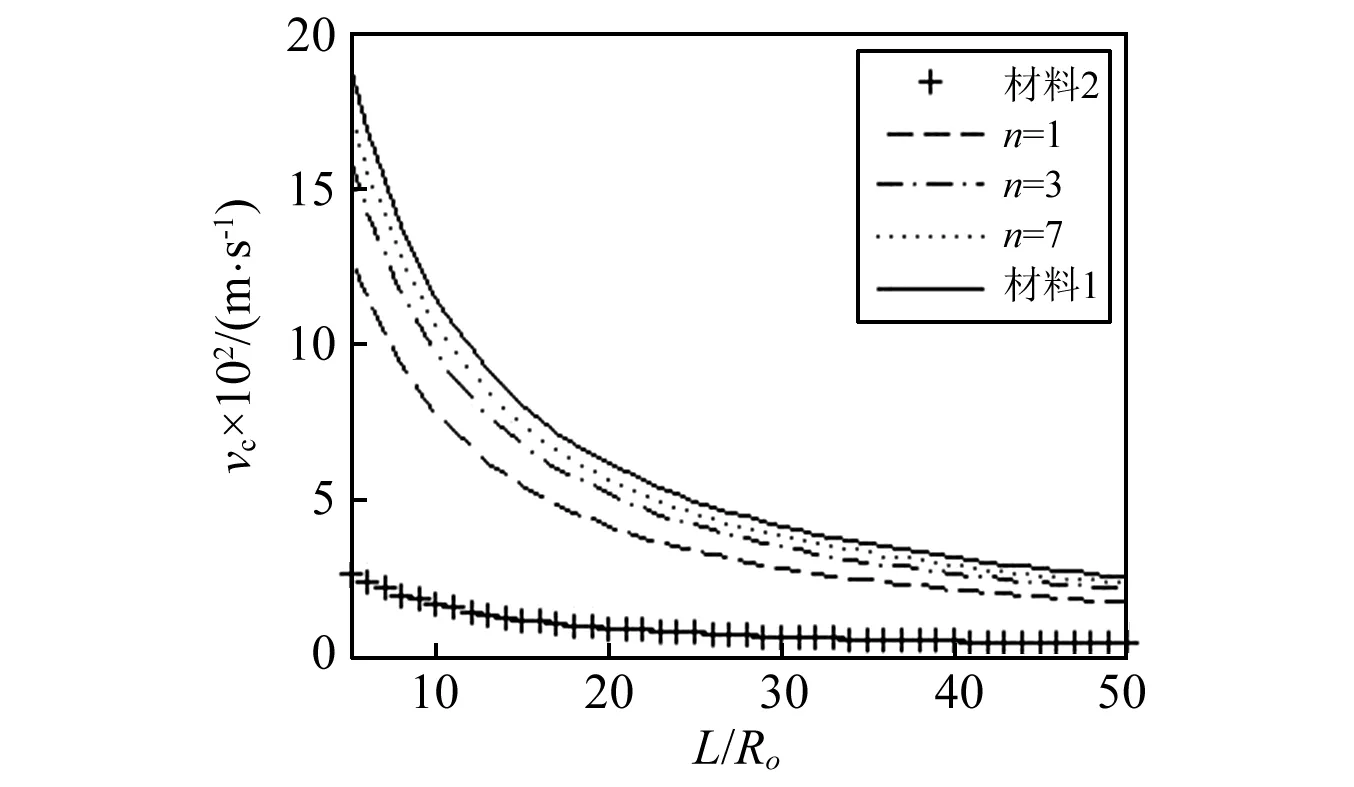
图8 不同功能梯度参数下,临界流速和L/Ro 的关系,其中Ro=1 cm, Ri=0.8RoFig.8 The relationship between critical fluid velocity and L/Ro under different FG parameters for Ro=1 cm, Ri=0.8Ro
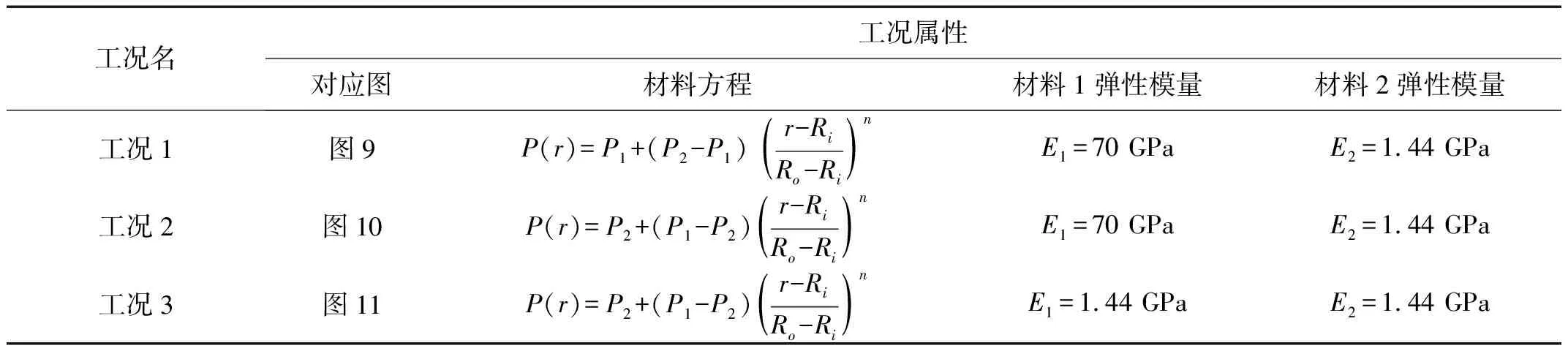
工况名工况属性对应图材料方程材料1弹性模量材料2弹性模量工况1图9P(r)=P1+(P2-P1) r-RiRo-Ri()nE1=70 GPaE2=1.44 GPa工况2图10P(r)=P2+(P1-P2)r-RiRo-Ri()nE1=70 GPaE2=1.44 GPa工况3图11P(r)=P2+(P1-P2)r-RiRo-Ri()nE1=1.44 GPaE2=1.44 GPa
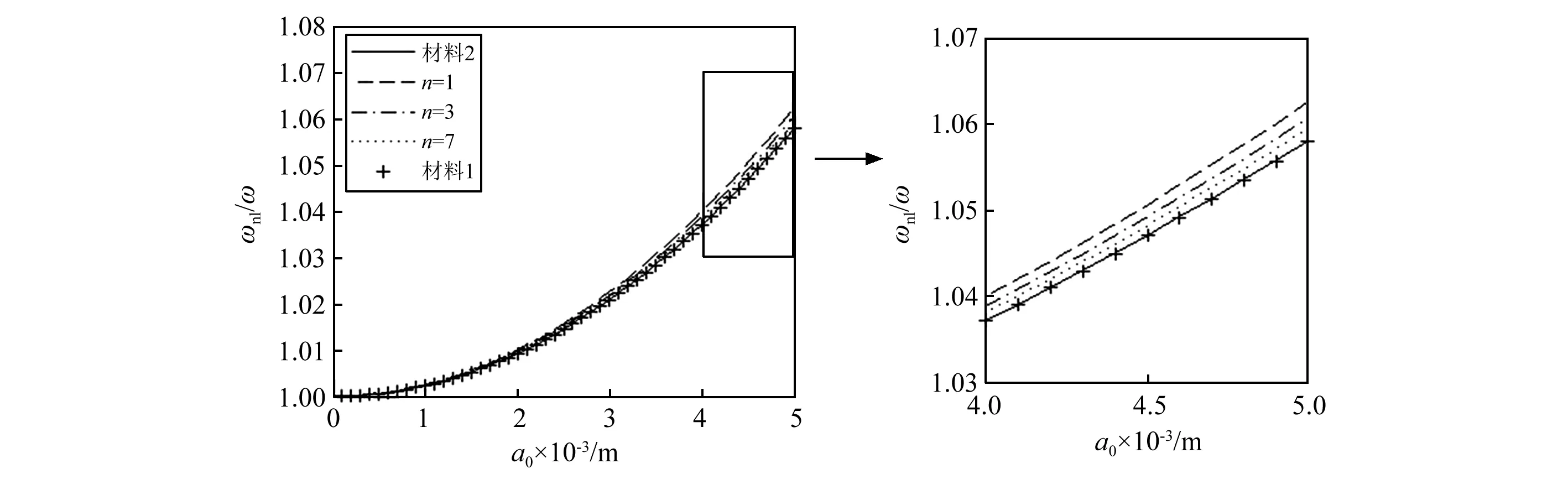
图9 不同功能梯度参数下,非线性频率和线性频率的比值与振幅的关系,其中Ro=1 cm, ρf=0, 材料工况1.右侧为局部放大图Fig.9 The relationship between ratio of nonlinear frequency to nature frequency and amplitude under different FG parameters for Ro=1 cm, ρf=0, materials condition 1. Partial enlarged drawing is on the right side
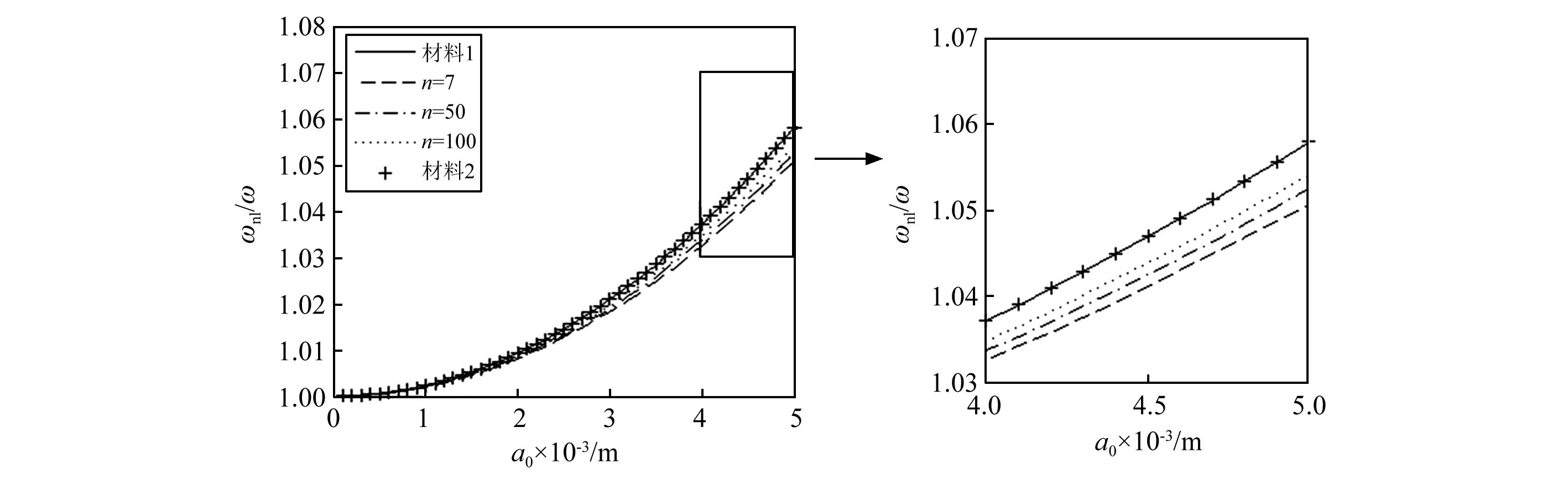
图10 不同功能梯度参数下,非线性频率和线性频率的比值与振幅的关系,其中Ro=1 cm, ρf=0, 材料工况2.右侧为局部放大图Fig.10 The relationship between ratio of nonlinear frequency to nature frequency and amplitude under different FG parameters for Ro=1 cm, ρf=0, materials condition 2. Partial enlarged drawing is on the right side
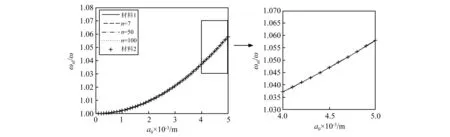
图11 不同功能梯度参数下,非线性频率和线性频率的比值与振幅的关系,其中Ro=1 cm, ρf=0, 材料工况3.右侧为局部放大图Fig.11 The relationship between ratio of nonlinear frequency to nature frequency and amplitude under different FG parameters for Ro=1 cm, ρf=0, materials condition 3. Partial enlarged drawing is on the right side.
4 结 论
本文应用一个适用于管的高阶梁模型,结合哈密顿原理,得到了功能梯度输流管在内流作用下的非线性控制方程。以两个变量之间频率关系的推导为基础,利用多尺度方法,求解了非线性耦合偏微分方程组,得到了管道自然频率和非线性频率的解析表达式。通过和已有文献的对比,验证了本文方法的正确性。由数值模拟可以发现,随着流速的增加,非线性频率与自然频率比值越来越大,且越靠近临界流速,变化越快,说明流体的存在使管道的非线性振动变得更加不稳定;当截面为单一材料的时候,非线性频率与自然频率比值随振幅的变化与材料性质关系不大,而功能梯度材料管截面不均匀性会导致频率比随振幅相应变化,且将弹性模量更大的材料放在管道的外侧,并取适当的功能梯度参数,可以一定程度的减小系统的非线性振动频率。功能梯度管道的这种表现较为特殊,计算结果对实际工程有一定的启示作用。
