基于优化分类的机械振动信号压缩感知

王 强， 张培林， 王怀光， 吴定海， 张云强

(军械工程学院 车辆与电气工程系，石家庄 050003)

近年来，随着计算机信息技术的不断提高，机械设备状态在线监测与故障诊断正朝向网络化、远程化、无线化方向发展[1-2]。在新的状态监测与故障诊断模式下，监测系统对机械设备信号采集与传输技术提出了更高的要求，同时，随着机械设备技术的改善，机械状态监测信号的带宽不断拓展，在传统奈奎斯特定理的信号采集模式下，信号采集将产生大量的状态监测数据，从而大大增加了信号存储与传输的难度。压缩感知是一种新兴的信号采集理论[3]，它突破了奈奎斯特采样定理对采样频率的限制，在压缩感知理论下，信号的采集过程能够实现采样与压缩的合并，从而大大节约信号存储空间、降低信号传输的数据量。

机械振动信号中包含了大量机械状态信息，因此是机械状态在线监测与故障诊断的重要依据[4]。由于机械设备自身结构复杂、工况恶劣，机械设备的机械振动信号表现为复杂的时域非稀疏信号，数据间相关性不明显[5]，因此给机械振动信号的压缩感知带来了巨大的困难。目前，众多学者对机械振动信号的压缩感知方法进行了探索，郭亮等[1]利用压缩感知原理实现了振动信号的数据压缩，取得了良好的效果，但是其采用的离散傅里叶变换稀疏字典的适应性有待进一步改进，佟路等[6]利用压缩感知原理实现了回转支承的信号采集，通过小波降噪的方式克服原始振动信号难以稀疏的问题，但这种方式在一定程度上增加了信号采集端的工作量与复杂度，王怀光等[7]结合阈值降噪的方法，利用提升小波实现了机械振动信号的压缩感知，取得了良好的压缩降噪效果，但其重构信号中部分有用信号丢失。可以看出，由于机械振动信号的特殊性，其稀疏字典的设计是实现振动信号压缩感知的关键，为此本文提出基于优化分类的机械振动信号压缩感知方法。该方法根据分块后信号的能量将不同信号块进行分类，采用量子粒子群 (Quantum Particle Swarm Optimization, QPSO)[8]的优化方法，在获得最佳的分类效果的同时，提高分类效率，并利用K-奇异值分解(K-Singular Value Decomposition, K-SVD)[9]的字典学习能力，获得与不同类信号相适应的稀疏字典，从而改进机械振动信号压缩感知效果。

1 机械振动信号压缩感知

压缩感知理论由Candes等[10-11]提出，由于其在欠采样条件下仍然能够保证原始信号的精确重构，因此得到广泛关注，并用在图像压缩[12]、医疗成像[13]等领域。机械振动信号压缩感知是压缩感知理论在振动信号处理领域的应用，根据压缩感知理论框架，机械振动信号压缩感知主要包括三部分内容：稀疏分解、压缩观测、信号重构。

机械振动信号稀疏分解是其实现压缩感知的前提条件，并直接影响到原始信号重构的效果。假设机械振动信号为x∈RN，将信号在正交字典下稀疏分解，稀疏字典为Ψ={Ψ1，Ψ2，Ψ3，…，ΨN}，则机械振动信号x可以表示为

(1)

式中：s为信号的稀疏系数向量，若机械振动信号在稀疏字典Ψ下具有稀疏性，则稀疏系数向量中包含了零元素或绝对值较小的元素。机械振动信号的稀疏性是其可压缩性的具体表现，当稀疏系数向量中非零元素以及绝对值较大元素的个数为K(K≪N)时，可近似地认为信号为K-稀疏信号。

压缩观测是信号压缩感知的具体实现方式，压缩观测的效果取决于测量矩阵的设计，假设机械振动信号测量矩阵为Φ，则对于上述K-稀疏信号，压缩感知可以表示为

y=Φx=ΦΨs=Θs

(2)

式中：y为观测信号；Θ为感知因子；Φ∈RM×N(M≪N)，M为观测数目，从式(2)可以看出，压缩观测的过程本质上是一个信号从N维降到M维的过程。

Candes等[11]指出，要实现原始信号的精确重构，测量矩阵必须充分保留原始信号的特性，即满足有限等距特性(Restricted Isometry Property, RIP)，并指出，矩阵元素独立同分布于高斯、贝努力等随机分布的测量矩阵，在观测数目M≥O(K×log(N/K))的条件下能够满足RIP性质，保证原始信号的精确重构。

经过压缩观测后得到的机械振动信号，在维度上大大降低，远小于原始的维度，因此原始信号的重构问题表现为病态，线性方程的个数远小于未知元素的个数，但由于机械振动信号具有稀疏性，因此在稀疏字典下稀疏系数向量的重构存在可能，机械振动信号重构模型可以描述为

s′=arg min‖s‖l0stΘs=y

(3)

式中：s′为稀疏系数重构向量， ‖s‖l0表示求解s向量中非零元素的个数。可以看出，信号重构为NP难问题，为此，Donoho等[14]提出将上述非凸优化问题转化为凸优化问题，即利用l1范数代替l0范数进行近似求解，从而降低原始信号重构的难度，并利用线性规划问题快速获得稀疏系数向量的重构结果，最后利用稀疏字典重构出原始信号。

2 自适应稀疏字典设计

由于机械设备结构复杂、工况恶劣，导致机械振动信号自身具有复杂性，因此其稀疏字典设计困难。现阶段，机械振动信号主要采用固定基字典，在一定条件下能够取得一定效果，但是固定字典适应性不强，稀疏分解效果有待于进一步改进，为此本文提出了自适应的稀疏字典设计方法，通过构造自适应稀疏字典，提高振动信号重构效果。

图1 自适应稀疏字典设计方法Fig.1 The design for adaptive sparse dictionary

自适应稀疏字典的设计方法如图1所示，从图中可以看出，该方法主要包括三部分内容：信号分割、QPSO优化分类、K-SVD训练字典。

2.1 信号分割

当测量的机械振动信号长度较大时，通常采样信号分割的方式，将长信号分割为相对较小的信号块，一方面通过信号分块的方式降低了测量矩阵构造的复杂度，降低了信号压缩感知的难度，另一方面，满足字典训练以及稀疏分解阶段，K-SVD算法对原始信号的结构要求，假设分块后信号块个数为T，则信号分割过程可以表述为：

x→X={x1,x2,…,xT}

(4)

式中：xi(i∈1,2,…T)表示第i信号块，对于分块后的信号，信号块的能量是衡量不同信号块结构特性的重要指标，对于能量相近的信号块，在信号形态上表现出相似性，按照能量分类能够将具有相似形态的信号块聚合到一起，通过这种细致的分类方式，能够有效提高字典训练阶段的收敛效果以及字典与原始信号的适应性，从而提高稀疏字典的质量。为此本文依据不同信号块的能量，将信号块进行分类。假设第i信号块能量为ei，则信号块能量序列可以表示为

E={e1,e2,…,eT}

(5)

假设信号分割长度为t，则式中ei为

(6)

2.2 QPSO优化分类

本文通过QPSO优化信号块分类过程，保证信号块分类效果，提高信号分类的效率。量子粒子群是粒子群算法的改进，通过引入量子理论，QPSO避免了传统粒子群算法容易早熟的问题，并且在计算复杂度上，由于QPSO操作算子少，计算简单，因此算法优化效率较高。

为快速实现信号块分类的目的，本文将信号块能量序列按照能量的大小进行排序，因此QPSO优化参数即为能量序列分类位置。假设分类个数为n，则待优化的位置参数个数为n-1，通过n-1个位置参数，可以将能量序列分割为n块，从而实现机械振动信号块分类的目的，因此设计量子粒子群单个粒子的信息为pi(T1,T2…Tn-1)，Ti表示第i-1类信号块与第i类信号块之间的分类位置。

QPSO优化的目标函数为不同类信号间能量均值的方差，从而保证不同类信号块之间的区分度：

(7)

式中：

(8)

ei表示第i类中所包含的所有能量序列，mean()表示求平均值，numel()表示求元素的个数，T表示信号块个数。

因此在QPSO优化分类过程中，以分类位置为待优化参数，以式(7)为目标函数，计算每个粒子的信息，并对粒子进行优劣评价。根据评价结果，确定每个粒子飞行的速度，完成粒子信息的更新，直至达到迭代条件，输出最终的分类位置，实现最佳的信号分类方式。

2.3 K-SVD训练字典

现有以固定字典为基础的稀疏分解方法适应性差，难以实现机械振动信号的有效稀疏分解，为此本文采用了基于K-SVD的稀疏字典构造方法，并将训练得到稀疏字典用于重构过程，改善机械振动信号重构效果。

针对上述分类后的机械振动信号块，对每一类信号块分别利用K-SVD算法训练得到稀疏字典，字典的训练过程中，字典原子的更新过程逐个进行，假设待训练的信号块为X，训练字典为Ψ，待更新字典原子为Ψi，则字典更新可以表述为：

(9)

式中：S为稀疏系数矩阵;sj表示矩阵S的第j行。通过对Ei进行奇异值分解，并利用奇异值分解后的奇异值向量对字典原子进行更新。当训练字典Ψ中各原子均得到更新时，即完成一次迭代过程，整个过程通过迭代次数Inum进行控制，当Inum达到预设值Imax后，迭代终止。根据经验值，文中将迭代次数预设值为20，此时既能够保证字典训练质量，又能够尽可能降低训练时间。

由于利用了机械振动信号块进行学习训练，因此获得的字典与原始信号的适应性较强，在字典下信号块能够获得良好的稀疏分解效果，在压缩感知重构过程中，与测量矩阵共同构造压缩感知因子，能够有效改善压缩感知重构效果。

3 压缩感知算法流程

稀疏字典设计是压缩感知的前提，在自适应的稀疏字典基础上，采用高斯随机矩阵作为测量矩阵，基追踪(Basis Pursuit, BP)算法作为重构算法，机械振动信号压缩感知算法流程如下：

步骤1将原始机械振动信号进行分块，求得每个信号块的能量，构造信号块能量序列e。

步骤2将能量序列按照能量由大到小进行排序，获得排序后的能量序列e′。

步骤3利用QPSO实现信号分类过程。

步骤4利用K-SVD获得不同类信号块的稀疏字典。

步骤5构造高斯随机测量矩阵，完成机械振动信号的压缩观测过程。

步骤6利用BP算法重构原始机械振动信号。

为评价压缩感知效果，定义评价指标压缩比CR以及峰值信噪比PSNR，压缩比为：

(10)

式中：n1、n2表示压缩感知前后机械振动信号的长度。

峰值信噪比为

(11)

(12)

4 实验与分析

实验数据为美国凯斯西储大学轴承实验中心滚动轴承实测信号，数据采集于滚动轴承振动实验台架，实验装置主要包括：感应电机、滚动轴承、自动校准联轴器、加速度传感器以及相关设备，实验装置如图2所示。滚动轴承采用了SKF公司生产的6205-2RS深沟球轴承，轴承主要参数如表1所示。

图2 振动实验台架Fig.2 The rig of vibration test

内圈直径/mm外圈直径/mm厚度/mm滚动体直径/mm节径/mm25.0052.0015.008.18244.20

实验过程中，振动实验台架工作载荷为2.2 kW，此时电机输出轴转速为1 730 r/min。实验故障采用电火花腐蚀的方式，分别在轴承外圈、内圈、滚动体上加工有凹槽，凹槽深度为0.053 mm，图3为实验台架在不同状态下的实验测量数据，信号采样频率为12 kHz，图中为0.5 s内信号的时域变化图。

图3 实测信号Fig.3 The measured signal

4.1 本文算法性能分析

为研究本文算法对机械振动信号的压缩感知效果，选取6 400个点作为样本信号。为尽量减少压缩感知后的数据量，信号分割过程中信号块之间不重叠，因此当信号分割长度l确定后，信号分块个数即为6 400/l。信号块的分割长度一定程度上影响了本文算法的性能，当l较小时，信号块个数多，量子粒子群粒子搜索范围偏大，并且压缩感知过程工作量增加，因此会导致机械振动信号的压缩感知效率降低，另一方面，当l增加时，测量矩阵中随机元素个数会不断增加，尽管分块压缩感知的方式能够有效降低测量矩阵的构造复杂度，但是随着信号块维度的增加，测量矩阵随机元素个数仍然呈线性增加，增加了存储压力，降低了矩阵构造效率。

图4给出了时间消耗随信号分割长度的变化情况，从图中可以看出，对于不同状态信号，当l小于16时，时间消耗随着信号分割长度的增加而不断降低，此时信号块个数较多，粒子群迭代过程与压缩感知过程的计算量较大，导致时间消耗较多，随着l的减少，信号块的个数不断减少，时间消耗不断降低。当信号分割大于16时，时间消耗趋于稳定，但当分割长度l进一步增加时，时间消耗又会缓慢升高，此时测量矩阵构造的复杂化导致单个信号块压缩与重构过程的时间消耗增加，因此算法的整体时间消耗体现出上升趋势。因此l取值16，此时算法的时间消耗最小。

图4 时间消耗Fig.4 The time consumption

针对上述滚动轴承实测信号，设置信号分割长度为16，则信号块个数为400，计算各信号块能量，构造能量序列如图5所示。

图5 能量序列Fig.5 The sequence of energy

以图5中信号块能量大小为分类依据，利用QPSO算法对400个信号块进行分类。设置QPSO粒子种群规模为100，记录粒子群每次迭代中的最优适应值，结果如图6所示，从图6中可以看出，随着迭代次数的增加，适应值体现出上升趋势，当迭代次数大于30时，仅有部分信号适应值没有收敛，变化缓慢，当迭代次数值大于40时，四种状态适应值几乎不再变化，因此设定迭代次数为40，此时既能够保证不同类信号间的分类效果，又能够提高分类效率，减少QPSO的时间消耗。

图6 迭代收敛效果Fig.6 Convergence effect of iteration

结合图3、5、6可以发现，QPSO分类效果与机械振动信号时域幅值、信号块能量的大小密切相关，时域信号幅值越大，分块后能量序列的幅值越大，QPSO分类后适应值越大。当滚动轴承工作在正常状态时，机械设备更多的受到噪声信号的影响，机械振动信号的结构特性与可稀疏性较差，信号分块后，能量序列规律性较差；当滚动轴承工作在故障状态时，故障信号明显改变了正常状态下信号的结构，在弱故障信号条件下，故障信号与正常信号、噪声信号混杂，信号在时域变得更加复杂，结构特性与稀疏性变差，而在较强故障信号的影响下，信号在时域幅值提升，分块后能量序列规律性增强，并且可以发现，故障信号的时域加速度幅值越显著，能量序列的规律性越强，此时故障信号一定程度上改进了机械振动信号的结构特性与可稀疏性，降低了噪声对机械振动信号的影响。

基于优化分类的压缩感知算法，其分类的个数是影响压缩感知效果的重要因素。当分类个数较大时，同属一类的信号块个数将会减少，字典训练过程中用于字典训练的样本将较少，则字典的训练质量将得不到保证，甚至存在训练样本过低而无法实现字典训练的情况。根据经验值，设定最大分类个数为12，则不同信号的压缩感知重构效果随分类个数的变化规律如图7所示。

图7 最佳分类个数Fig.7 The best number of classification

从图7中可以看出，滚动体故障、内圈故障、外圈故障、正常状态的最佳分类次数分别为9、2、5、3。而在PSNR数值上，PSNR(内圈故障)> PSNR(正常状态)>PSNR(外圈故障)>PSNR(滚动体故障)。压缩感知采用了K-SVD稀疏字典，由于K-SVD具有自适应的学习能力，在自适应稀疏分解过程中，结构性越强的信号在K-SVD下稀疏分解越好，字典质量越高，因此其重构PSNR的大小可以作为衡量信号结构特性的指标，对于上述四种滚动轴承振动信号，可以认为在信号的结构特性上，内圈故障信号最优，其次为正常信号，滚动体故障信号最差。因此可以得出结论，对于结构特性好的信号，最佳的分类个数少，信号结构特性越差，最佳的分类个数越多。

在最佳的分类个数条件下，设定压缩比CR为2，压缩感知效果如表2所示。实验过程中增加了未经分类以及随机分类的机械振动信号压缩感知作为对比，表中△PSNR为本文算法相对于未分类的压缩感知重构信号PSNR的提升值。

表2 压缩感知效果(PSNR/dB)

表2中可以看出，本文算法的重构PSNR最高，好于未分类以及随机分类的重构效果，证明了本文优化分类的压缩感知算法的有效性。相对于未经分类的压缩感知效果，在PSNR提高值上，△PSNR(滚动体故障)>△PSNR(外圈故障)>△PSNR(正常状态)>△PSNR(内圈故障)，PSNR提高值的大小顺序与PSNR数值的大小顺序相反，结合PSNR大小与信号结构特性的对应关系，可以得出结论，本文算法对结构特性较差的信号PSNR提升效果明显。

相比于未经分类的K-SVD算法，本文算法有效提升了信号的重构PSNR，但同时也增加了算法的复杂度，降低了算法的运行效率，在相同的硬件条件下，算法的运行时间是算法复杂度的一个重要体现，针对上述滚动体故障信号，本文比较了在不同信号长度下本文算法相对于未经分类的K-SVD重构信号的PSNR变化量△SNR以及算法运行时间变化量△t：

(13)

(14)

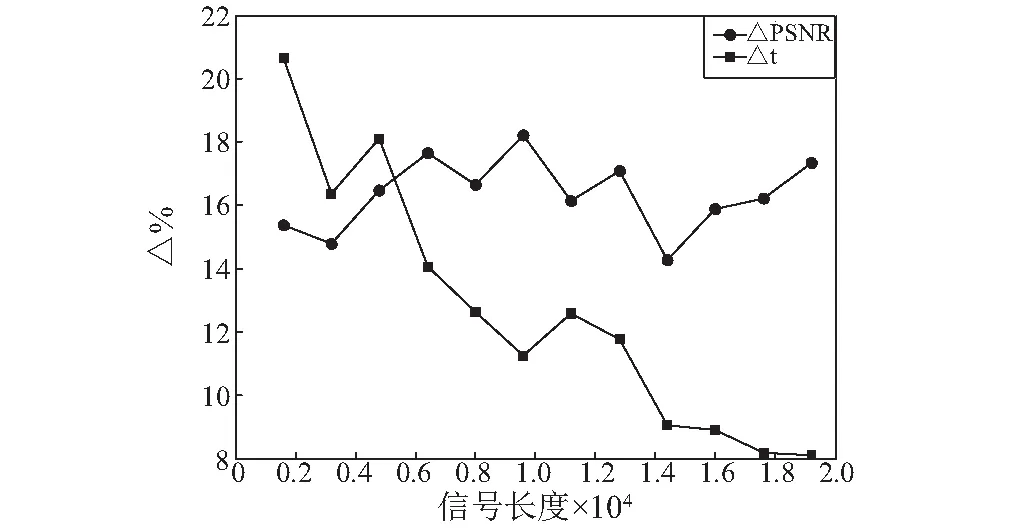
图8 △PSNR以及△t随信号长度的变化Fig.8 △PSNR and △t with the change of signal length

从图8中可以看出，随着信号长度的增加，△PSNR波动幅度较小，平均值为16.58%，而△t随着信号长度的增加而不断降低，直至趋近于0%。可以看出，相对于未经分类的K-SVD，虽然本文算法一定程度上增加了运行时间，但当信号长度过大时，时间增量△t很小，而△PSNR基本不随信号长度的变化而发生变化，因此在处理大长度信号时，本文算法在牺牲少量运算效率的条件下，能够大幅提升信号重构效果。

4.2 对比验证

针对上述不同状态轴承振动信号，采用不同压缩感知算法作对比，观察信号在不同长度、压缩比条件下的重构PSNR。对比算法分别采用了文献[15]中基于DCT的压缩感知方法、文献[16]中基于小波基的压缩感知方法以及文献[17]中基于K-SVD的压缩感知方法，基于K-SVD的压缩感知方法实质上等同于上述未经分类的压缩感知方法。实验结果如表3所示。

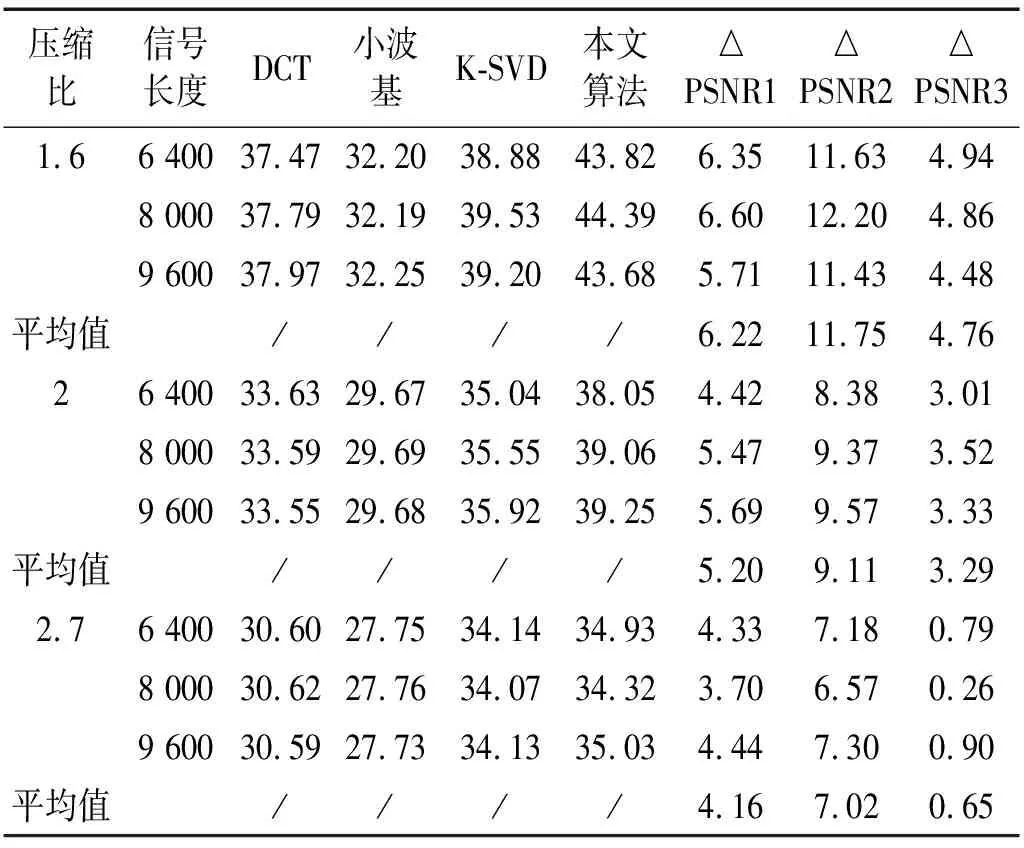
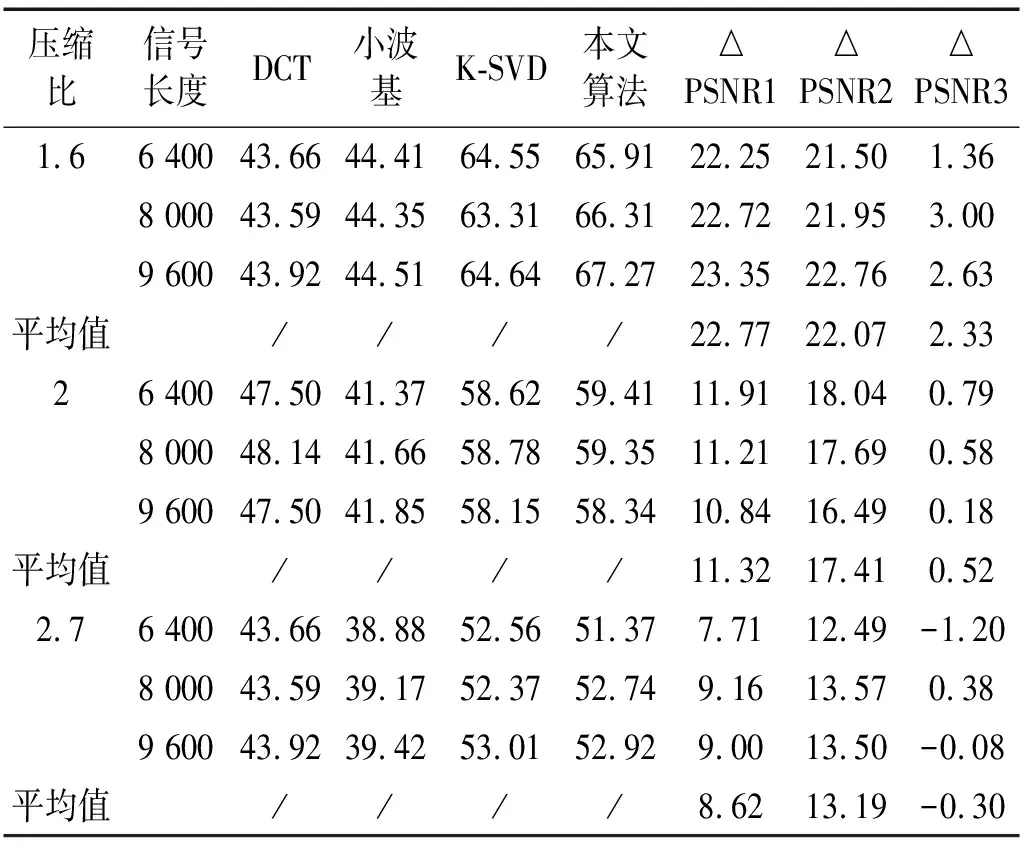
表3 不同算法性能对比(PSNR/dB)

(b) 内圈故障

(c) 外圈故障

(d) 正常状态

表3中△PSNR1、△PSNR2、△PSNR3分别表示本文算法相对于DCT、小波基、K-SVD的PSNR增量。从表中可以看出，对于同一种信号，在压缩比相同时，信号的长度对信号的压缩感知效果影响不大，在信号长度相同时，压缩感知效果随压缩比的增加而不断降低。信号的结构特性对压缩感知的效果影响作用较大，对于弱故障信号(滚动体故障、外圈故障)，在不同压缩比下，信号重构效果较差，对于强故障信号(内圈故障)或者正常信号，信号重构效果较好，结论与前文相一致。对比不同算法，可以发现，对于不同状态信号，采用自适应学习字典的K-SVD与本文算法的重构PSNR明显高于采用固定字典的DCT、小波基，特别是对于强故障信号、低压缩比状态，PSNR提升明显。对比K-SVD与本文算法，可以发现，本文算法有效改善了K-SVD对弱故障信号在压缩感知重构中存在的不足，如在压缩比为1.6的滚动体故障信号压缩感知重构中，本文算法相对于K-SVD的PSNR平均提升量达到4.76 dB。同时，从表中可以看出，压缩比对本文算法的性能有所影响，在压缩比较小时，本文算法相对于K-SVD的改进效果明显，综上所述，本文算法更适用于低压缩比的情况。

4.3 实测信号验证

为进一步验证本文算法的有效性，对实测发动机曲轴轴端信号进行压缩感知，对比不同算法的压缩重构效果。发动机为三缸柴油机，传感器采用的是YD-181型加速度传感器，设置发动机分别工作在正常状态、单缸失火、两缸失火状态，实测信号，如图9所示。

图9 曲轴轴端信号Fig.9 The signal of the crankshaft end

从图9中可以看出，发动机在工作过程中产生强烈的振动信号，由于发动机特殊的工作过程，曲轴轴端信号在时域存在周期性的冲击信号，这种冲击信号在一定程度上使得振动信号具有较好的结构特性与稀疏性，有利于信号的压缩重构。针对上述信号，取信号长度为6 400，根据经验设定压缩比为2，比较不同算法的压缩感知效果。信号重构的PSNR如表4所示，从表中可以看出，本文算法的重构效果最好，同时，采用训练字典的K-SVD与本文算法明显好于采用固定字典的DCT与小波基，对比K-SVD与本文算法，可以发现在K-SVD的重构PSNR较小时，本文算法相对于K-SVD的改善效果较好，实验结果与前文一致，因此本文算法能够有效改善发动机曲轴轴端振动信号压缩重构的效果，算法的有效性得到进一步验证。

表4 压缩感知效果(PSNR/dB)

5 结 论

针对复杂机械时域振动信号复杂、数据间相关性差导致的信号稀疏困难、压缩感知效果差的问题，提出了基于优化分类的机械振动信号压缩感知算法。本文算法在信号分块的基础上，以信号块的能量为依据，采用QPSO优化算法，将信号块进行分类。分类后不同类信号间能量均值的方差达到最大，保证不同类信号之间充分区分。最后利用K-SVD训练生成与不同类信号相适应的稀疏字典，提高了机械振动信号在字典下的稀疏效果，从而改善压缩感知信号重构效果。通过滚动轴承在不同状态下实测信号的压缩感知实验，充分验证了本文算法有效性。