盲VMD-Cepstral在轴承故障诊断中的应用*

柏 林， 唐 智, 徐冠基

(重庆大学机械传动国家重点实验室 重庆，400044)

引 言

1998年，Huang等提出了一种时频处理方法EMD,并指出EMD存在严重的模态混叠以及抗噪效果差等缺点。2014年，Dragomiretskiy等[1]提出一种新的信号分解估计方法VMD，主要通过迭代搜寻变分模型的最优解，得到每个分量的中心频率以及带宽，从而有效分离各分量。Mohanty等将EMD和VMD在轴承故障诊断中的应用进行了对比，VMD相对于EMD具有噪声鲁棒性好、无端点效应等优点；但VMD分解也存在其固有缺陷，例如需要确定参数二次惩罚因子α以及分解层数k，并要对其进行优化选择，否则模态混叠现象无法避免，且文中对于VMD参数的确定并未给出。刘长良等[3]将VMD结合模糊C均值聚类应用在轴承故障诊断中，但是k的确定依靠分解后得到的分量是否存在过分解来判断k值是否合适，且没有有效的α确定方法。目前，有文献针对其参数进行优化，如唐贵基等[5]利用粒子群优化算法对VMD参数进行寻优，取得了较好的效果，但寻优过程增加了VMD分解的时长，存在时效性上的损失。文献[6]将改进后的VMD与奇异值差分谱结合来分解和重构信号，达到判断轴承故障类型的目的。如何在无先验知识的情况下提高VMD在工程中的适用性，成为当前研究的热点。解决的方法有两种：a.采用智能计算对其参数进行优化；b.采取后处理的方法对参数未优化的盲分解所得分量进行再分离重构。

VMD在故障分析中存在的一个瓶颈是如何进行故障敏感分量的选择，特别是对于早期故障，其特征往往较为微弱，难以用特定的某个参数指标进行准确筛选。传统解决问题的方法主要是对参数指标进行优化选择或对特征频带进行解调分析，如对振动信号进行EMD或VMD分解后，选择峭度值最大的分量进行故障频带甄别。但机械故障信号经VMD分解出的分量频带分布比较复杂，故障分量与干扰分量的频带往往相互交叠，振动信号的故障特征频带可能存在于多个分量之中，故需要对分解得到的分量进行筛选。由于被分析信号中脉冲类噪声的影响，有可能使非故障分量峭度偏大，甚至超过故障冲击频带。因此，有必要在无故障频带先验知识的情况下，进行故障特征的盲提取。

基于以上分析，笔者采用对未经参数优化的VMD分解获取的分量进行PCA[7]处理，将相关变量映射为不相关的变量，采用熵值指标滤出噪声干扰分量。针对故障频带难以确定及参数指标优化选择难的问题，笔者从采用倒谱包络的方法对重构信号进行二次分析，在无需甄别故障分量的情况下进行故障频率的准确识别，最终达到无先验知识，无需任何参数的优化与故障频带选择进行双盲状态下的滚动轴承微弱故障特征的有效提取，实现故障类型的准确辨识。

1 VMD基本理论

变分模态分解是一种新的信号分解估计的方法，其分解主要是变分问题的求解过程，使每一个模态的估计带宽之和最小。

VMD首先采用式(1)进行变分模型的构造

(1)

将式(1)由约束变分问题转变为非约束变分问题，转化之后的拉格朗日方程为

(2)

其中：λ为拉格朗日乘子；α为二次惩罚因子；f为原始信号。

在构造变分模型的基础上，VMD的求解主要采用交替方向乘子法求式(2)的鞍点及拉格朗日方程的最优解。具体实现方法如下：

2) 执行最外层循环，n=n+1；

3) 执行内层第1个循环，循环次数为k=1,2,…,K,当ω≥0时更新uk和ωk

(3a)

(3b)

4) 最外层循环执行

循环终止条件

(4)

2 VMD-Cepstral轴承故障诊断方法

从VMD的分解过程可知，惩罚因子α和分解层数k的选择是VMD分解结果是否存在混叠的关键。如何从VMD盲分解结果中最大化地提取出故障信息，是VMD分解后处理的核心。由于VMD盲分解得到的分量往往存在着模态混叠的现象，即故障特征分量可能仍隐藏或分散在VMD分解分量中。为了能提取出有效的故障信息，笔者采用PCA矩阵变换，将相关的变量映射为不相关的分量，达到混叠模态分离及降维的目的。为滤除与故障冲击频带无关的频段，且考虑到峭度易受到离群野值的影响，而信息熵[8]可以在无信号先验及低信噪比情况下，对特征频带与噪声进行区分，故采取分量熵值筛选方法对PCA有效分量进行筛选与重构。

笔者采用包络谱熵[9]进行噪声的分离，若分量频率分布比较规律，则熵较小；若噪声分量成分复杂无规律，幅值相对平坦，则熵值较大。因此，可根据熵值的大小来量化PCA分量中包含的故障信息，用于VMD分解中噪声隔离，以达到噪声抑制及故障特征增强的目的。最后，为避免传统轴承故障信号分析中的故障频带选择带来的特征提取偏差问题，结合倒谱包络分析对重构信号进行故障频率特征提取，倒谱包络解调是一种无需确定故障频带即可进行调制频率的鲁棒提取方法。

VMD-Cepstral信号分析方法的具体实施过程如下。

1) 对信号进行标准化，消除量纲和数量级对故障特征分析的影响，其过程为

(均值)

(5a)

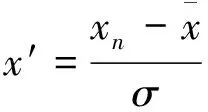
(5b)

其中：xn为原始振动信号；x′为标准化后的信号。

2) 对标准化后的信号按照式(1)～式(4)的方法进行VMD分解。

3) 对VMD分量进行PCA分解[6]，将高维空间映射到低维空间。

4) 计算PCA分量的包络谱熵，筛选出熵值小于所有PCA分量信息熵均值的分量，对筛选得到的信号分量进行重构。信息熵计算公式为

(6)

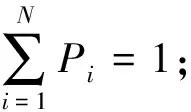
5) 对重构信号进行倒谱包络解调，提取故障特征频率。

3 滚动轴承故障分析

用于实验的滚动轴承振动信号数据来自Case Western大学的轴承数据中心[9]。故障轴承类型为6205-2RS，使用加速度传感器进行数据采集，采用电火花加工技术使轴承产生单点缺陷，实验数据为滚动轴承故障直径为0.177 8 mm时采集的内圈故障与滚动体振动数据，以此验证本研究方法。工况如下：空载；转速为1 797 r/min。

根据轴承的转速以及轴承的尺寸参数，得到轴承内圈与滚珠的故障频率分别为162.1与141.17 Hz，转频为29.88 Hz。采用本研究方法对图1中的内圈故障信号进行分析。从图1(a)的时域波形可以看出，内圈缺陷造成的冲击微弱，且淹没在大量干扰噪声中。从其频谱图1(b)中可看出，频带分布结构复杂，在1 000，2 800及3 400 Hz附近都出现了密集的频带分布，且强度相近，频带交叠，无法判别故障冲击频带，给传统的故障频带滤波带来一定困难。

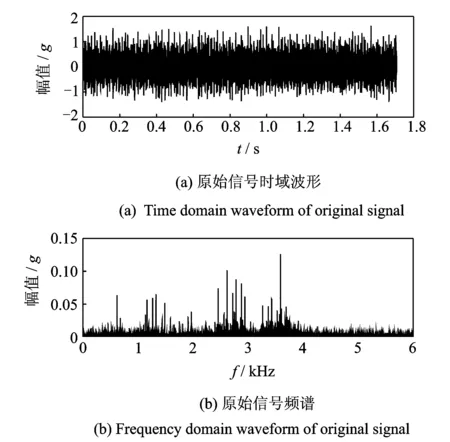
图1 原始信号时频域信息Fig.1 The time domain and frequency domain information of original signal

采用本研究方法对图1中时域信号进行VMD分解，分解结果如图2所示。从各分量的频谱图可看出，未经参数优化的VMD将原始信号进行了从低频到高频的分解，最终得到6个VMD分量。

图2 VMD分解结果Fig.2 The results of VMD

由图2可以看出，分量3与分量4、分量5与分量6中心频率比较接近，存在频带交叠现象。出现该情况的原因是k值选取过大，导致出现过分解的情况，因此后续有必要对VMD分量进行PCA处理。PCA主元个数的选择主要依据累计贡献率，解决实际问题时，一般选取n个主元，使累计方差贡献率达到一定要求(通常80%以上)。每个主元的贡献率如图3所示。

根据帕累托图可以看出，前5个主元的累计贡献率已达到85.35%，故选择前5个主元进行包络谱熵计算。计算出的各PCA分量包络谱熵值如表1所示。

由表1可知，主元包络谱熵的均值为0.399 4；主元2的包络谱熵最大，包含的噪声成分较多；主元4熵值最小，频率成分较为稳定。选择主元熵值小于各分量信息熵均值的主元进行信号的重构，重构信号如图4所示。

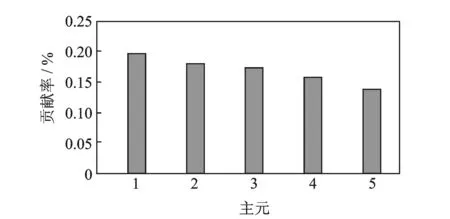
图3 主元贡献率Fig.3 The contribution rate of principal component

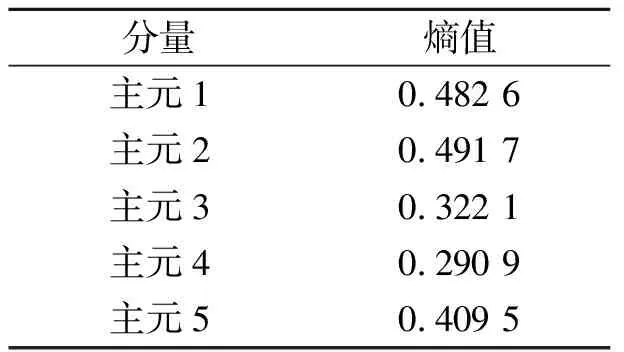
表1 各主元的包络谱熵值

图4 内圈故障信号重构后时频域信息Fig.4 The time domain and frequency domain information of the reconstructed signal in inner race faults

对比图4和图1可知，重构后信号的频带集中，冲击频带已被隔离出来，噪声得到了有效抑制。最终将传统处理方法与本处理结果进行对比，图5(a)为采用EMD分解之后，选择峭度最大的分量进行包络解调分析；图5(b)为对VMD分量进行后处理重构信号的倒谱包络图。

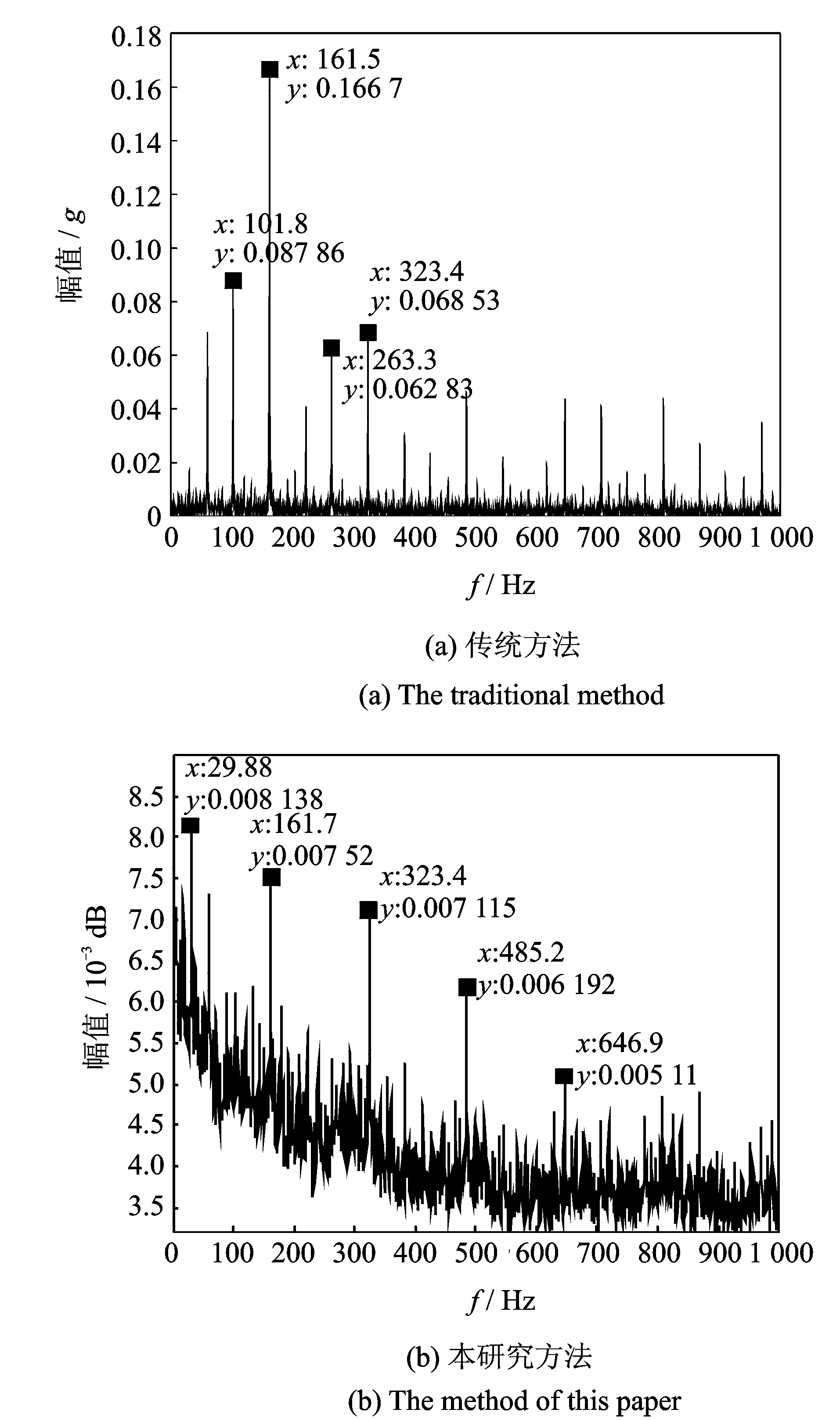
图5 方法对比Fig.5 Comparison of the two methods

通过比较图5(a)和(b)可知：传统分析方法虽然能识别出故障频率161.5 Hz，但解调谱中出现了部分干扰频率，如101.8和263.3 Hz，且对应幅值较大，转频30Hz以及谐波成分也未能体现。相对于图5(a)，图5(b)对重构信号的倒谱包络处理后得到的故障频率更加明显，其谐波频率323.4，425.2和646.9 Hz也得到更好的呈现，并没有出现多余的干扰频率成分。从重构倒谱中还可获得更加丰富的信息，如滚动轴承的转频等，故障可识别性与准确性得到一定的提高。

为了进一步验证本研究方法的有效性与适用性，下面采用本方法对轴承滚动体故障信号进行分析，整个处理过程进行简化后给出。

图6为滚动体故障振动信号时域波形与传统包络解调谱。由于滚动体故障冲击微弱，从图6包络解调谱中无法读取对应的故障频率。

图6 原始信号信息Fig.6 The information of original signal

对VMD分解之后的6个分量进行PCA去相关处理，计算包络谱熵值，得到主元1～主元6熵值分别为0.608 1，0.427 7，0.390 7，0.645 2，0.642 6及0.486 3,包络谱熵的均值为0.533 5。将筛选的分量进行重构，重构信号的时域波形和频谱如图7所示。

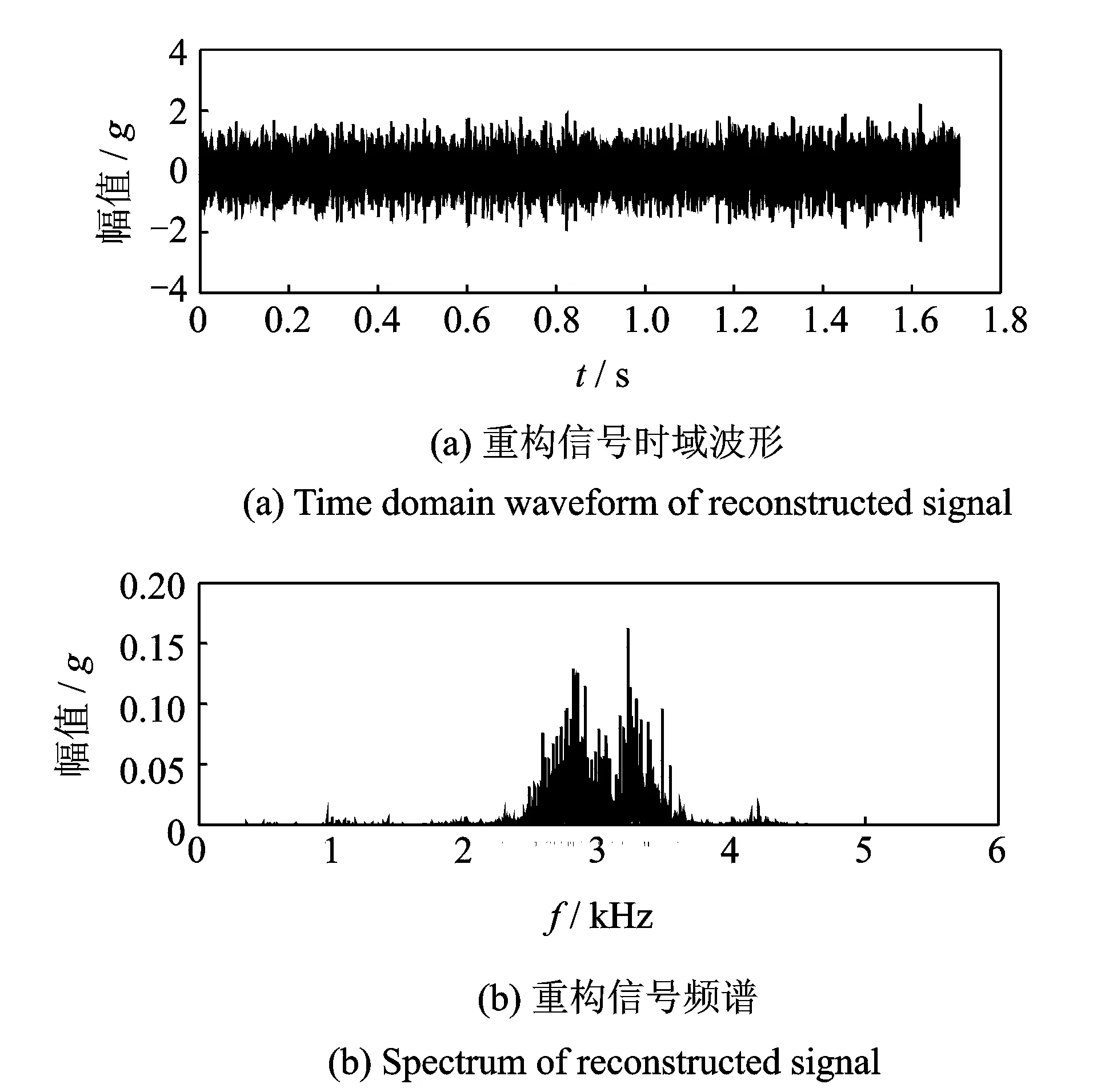
图7 滚动体故障信号重构后时频域信息Fig.7 The time domain and frequency domain information of the reconstructed signal in ball faults

由图7可以看出，通过VMD分解以及PCA去相关后，对噪声的抑制比较明显，能有效提取出故障冲击频带。对重构信号计算倒谱包络，结果如图8所示。

图8 重构信号倒谱包络Fig.8 The cepstral envelope of reconstructed signal

由图8得到峰值对应的频率为29.88，59.77，89.65，119.5及141.4 Hz。与图6原始信号的包络谱对比可看出，用本研究方法处理之后的谱图故障信息更加明显，能有效地辨识出转频与故障频率，从而提高轴承故障诊断准确率。

4 结 论

1) VMD是一种对变分约束模型求解过程，通过迭代更新将信号的各个模态估计出来，其本质为自适应的维纳滤波器组，各个模态代表着不同的中心频率。

2) 运用本研究方法分析滚动轴承内圈和滚动体可知，采用VMD-Cesptral通过倒谱包络能有效提取出信号中的故障信息。

3) VMD的不足是需要事先确定α和k，但笔者运用PCA、熵值对分量进行后处理，而不需优化α和k来达到较好的诊断效果。

4) VMD-cepstral能有效地提取出滚动轴承的故障频率，从而判断出滚动轴承的损伤位置，对不平衡故障具有较好的诊断效果，并且具有良好的抗噪能力。

参 考 文 献

[1] Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society of London, 1998, 454(12):903-995.

[2] Dragomiretskiy K, Zosso D. Variational mode decomposition[J]. IEEE Transactions on Signal Processing, 2014，62(3)：531-544.

[3] Ram R, Mohanty M N. Comparative analysis of EMD and VMD algorithm in speech enhancement[J]. International Journal of Natural Computing Research, 2017, 6(1): 17-35.

[4] 刘长良, 武英杰, 甄成刚. 基于变分模态分解和模糊C均值聚类的滚动轴承故障诊断[J]. 中国电机工程学报, 2015, 35(13):3358-3365.

Liu Changliang, Wu Yingjie, Zhen Chenggang. Rolling bearing fault diagnosis based on variational mode decomposition and fuzzy C means clustering[J]. Proceedings of the SCEE, 2015, 35(13):3358-3365.(in Chinese)

[5] 唐贵基, 王晓龙. 参数优化变分模态分解方法在滚动轴承早期故障诊断中的应用[J]. 西安交通大学学报, 2015, 49(5):73-81.

Tang Guiji, Wang Xiaolong. Parameter optimized variational mode decomposition method with application to incipient fault diagnosis of rolling bearing[J]. Journal of Xi′an Jiaotong University, 2015, 49(5):73-81.(in Chinese)

[6] 唐贵基, 王晓龙. IVMD融合奇异值差分谱的滚动轴承早期故障诊断[J]. 振动、测试与诊断, 2016,36(4):700-707.

Tang Guiji, Wang Xiaolong. An incipient fault diagnosis method for rolling bearing based on improved variational mode decomposition and singular value difference spectrum[J]. Journal of Vibration, Measurement & Diagnosis, 2016,36(4):700-707. (in Chinese)

[7] Wold S, Esbensen K, Geladi P. Principal component analysis[J]. Chemometrics & Intelligent Laboratory Systems, 1987, 2(1):37-52.

[8] 潘宏侠, 都衡, 马春茂. 局域波信息熵在高速自动机故障诊断中的应用[J]. 振动、测试与诊断, 2015,35(6):1159-1164.

Pan Hongxia, Du Heng, Ma Chunmao. High-speed automaton fault diagnosis based on local wave and information entropy[J]. Journal of Vibration, Measurement & Diagnosis, 2015,35(6):1159-1164. (in Chinses)

[9] 潘玉娜, 陈进. 包络谱熵在滚动轴承性能退化评估中的应用[J]. 上海应用技术学院学报:自然科学版, 2014, 14(3):220-223.

Pan Yuna, Chen Jin. Application of envelope spectral entropy to rolling bearing performance degradation assessment[J]. Journal of Shanghai Institute of Technology:Natural Science, 2014, 14(3):220-223.(in Chinese)

[10] Loparo K A．Bearings vibration data set，Case Western Reserve University[EB/OL]．(2016-07-03). http:∥www.eecs.cwru.edu/laboratory/Bearing /download.htm．