非下采样轮廓波变换在故障分类中的应用*

李宏坤， 崔明利， 杨 蕊， 张志新， 王奉涛

(1.大连理工大学机械工程学院 大连，116024) (2.大连大学机械工程学院 大连，116622)

引 言

在信号处理领域，时频分析方法得到了广泛的应用，能够克服传统的时域、频域等方法的缺陷，因此在设备故障诊断领域得到了广泛的研究[1]。张梅军等[2]指出连续小波灰度图不但能够提取表示周期性冲击的故障信息，而且能够直观地表达出信号的细微差异结果，但此方法仅停留在对故障信息直观观察的阶段，并未进一步深入研究。因此，探索基于振动信号时频图像处理与分析的新方法、新技术以及发展新的特征提取理论与技术就显得尤为重要。Renata等[3]利用图像处理的方法进行早期轴承故障诊断。Wang等[4]提出基于时频图像处理的方法对齿轮早期故障进行了识别。章立军等[5]研究了基于时频图像融合技术提取轴承性能退化特征。吕琛等[6]通过时频图像处理技术对柴油机主轴磨损进行了检测识别。

时频图像信息是一类表达故障信息的重要形式，将基于图像处理的识别技术应用于故障诊断中，可以更加准确和及时地指导工作人员进行设备维修。文献[7-8]提出了轮廓波变换，该变换由于在变换过程中需要上下采样，会产生Gibbs效应而不具有平移不变性。为了弥补该问题，产生了非下采样轮廓波变换。非下采样轮廓波变换可认为是轮廓波变换的的提升，基于非下采样轮廓波变换具有平移不变性，能够实现对图像的多方向和多分辨率分解特性。王常青[9]研究了非下采样轮廓波变换在轴心轨迹特征提取中的应用。贾函龙等[10]利用非下采样轮廓波变换对人脸分割的局部图像进行特征提取并取得了较高的准确率。崔克彬等[11]提出了一种基于非下采样轮廓波变换的图像增强算法实现了对电气设备热故障自动诊断与定位。笔者提出将时频图像与非下采样轮廓波变换相结合的故障分类方法,结果表明，所提出基于时频图像和非下采样轮廓波特征的故障分类方法具有较高的识别率，可有效地用于设备的状态识别。

1 振动信号的时频图像

时频分析即是时频联合域分析的简称，作为一种新兴的信号处理方法，近些年来受到较多的关注。时频分析能够将振动时域信号转换为时频域形成时频图像，时频图像则提供了时间域与频率域的联合分布信息，能够描述信号频率随时间变换的关系。连续小波变换方法在高频部分具有很好的时间分辨率，在低频部分具有很好的频率分辨率[12]，因此，笔者选用连续小波变换作为获取时频图像的方法，其表达式为

(1)

图1所示为某齿轮3种不同程度裂纹的时域信号经过连续小波变换后所得到的连续小波时频图像，变换时所采用的小波函数为“cmor3-3”。从时频图像中可以看出存在一定差异， 因此需要进一步进行特征提取描述其不同状态。

图1 不同状态的小波时频图像Fig.1 Different wavelet time-frequency image

2 非下采样轮廓波变换

2.1 非下采样轮廓波变换原理

轮廓波变换是一种二维图像的表示方法，该变换先利用拉普拉斯金字塔进行多尺度分解，以捕获奇异点，再利用方向滤波器进行方向性分解，将分布在不同方向上的不连续奇异点连成线性结构[13]。由于在尺度分解和方向分解过程中会有上下采样，产生Gibbs效应，不具有平移不变性。为克服这个问题，Arthur等[14]提出了非下采样轮廓波变换。

非下采样轮廓波变换是利用非下采样金字塔(non-subsampled pyramid, 简称NSP)和非下采样方向滤波器(non-subsampled directional filter bank, 简称NSDFB)完成的，其中NSP能够对时频图像进行多尺度分解，NSDFB则可将由NSP分解后产生的高频系数进行多方向分解。由于分解过程中没有下采样操作，因此非下采样轮廓波变换能够克服Gibbs效应，因而具有平移不变性。综上可知，非下采样轮廓波变换能够更好地进行图像处理。图2所示为非下采样轮廓波变换的两层分解。

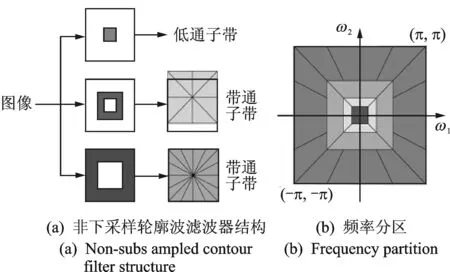
图2 非下采样轮廓波变换示意图Fig.2 Non-subsampled contourlet transform decomposition chart

2.2 时频图像的非下采样轮廓波变换

笔者将由振动信号通过连续小波变换得到的时频图统一保存为512×512像素大小的图片，然后通过Matlab将时频图像转化为灰度图，以便进行非下采样轮廓波变换，图像经过非下采样轮廓波变换分解后所得到的各子带分量大小与原图像一致。为了更加有效地提取时频图像的纹理特征，使用非下采样金字塔将时频图像的灰度图分解为2个尺度，然后由非下采样方向滤波器组将得到的高频子带分别分解为4和8个方向。通过以上分解后，会得到1个低频子带，第1层的4个方向的高频子带，第2层的8个方向的高频子带。图3所示为某一时频图像对应灰度图的非下采样轮廓波变换的子带部分。

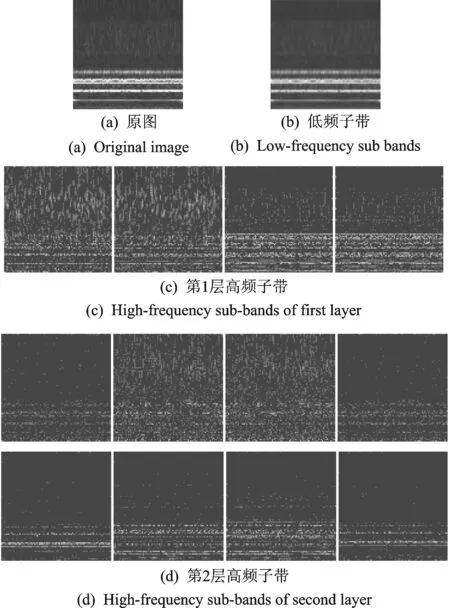
图3 非下采样轮廓波变换子带Fig.3 Non-subsampled contourlet transform sub-band

2.3 特征量提取

非下采样轮廓波变换后得到的低频子带能够反映时频图像的平均和近似特性，表示图像的模糊轮廓信息。均值和标准差反映的是一种全局特征，因而提取低频子带的均值和标准差作为特征量。均值的计算公式为

(2)

其中：xij为低频子带各系数；M×N为子带方阵的大小。

由标准差定义可知，若低频子带的标准差越大，则其灰度就越离散，图像也就具有更多的纹理信息。标准差计算公式为

(3)

其中：xij为低频子带各系数；μ为均值；M×N为子带方阵的大小。

非下采样轮廓波变换后得到的高频子带能够反映时频图像的纹理和边缘等细节信息，而能量是对纹理细节的一种描述，因此，笔者提取各层子带的能量均值作为特征量。各子带能量的计算公式为

(4)

其中：k为某层下第k个高频子带；xij为第k个高频子带各系数；M×N为子带方阵的大小。

第1层高频子带的能量均值计算公式为

(5)

第2层高频子带的能量均值计算公式为

(6)

综上可知，每个振动信号的时频图像可以得到一个4维的特征向量

F=[μ,δ,e1,e2]

(7)

3 支持向量机

SVM作为一种基于统计学习理论的机器学习方法，通过寻求结构化风险最小来提高学习机泛化能力，实现经验风险和置信范围的最小化，可在统计样本量较少的情况下获得良好统计规律。图4所示为线性可分模式下二维输入空间中最优超平面几何结构，加号和圆圈代表两类样本，H为分类线，H1和H2分别为过各类中离分类线最近的样本且平行于分类线的直线，两者之间的距离叫做分类间隔，H1和H2之上的样本就称为支持向量[15]。

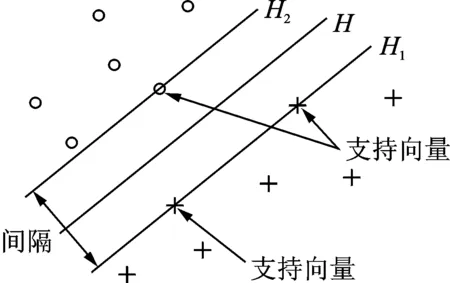
图4 最优分类面Fig.4 Optimal separating plane

对于分类问题，支持向量机仅考虑了二值分类的简单情况，而对于机械故障分类等多值分类问题时，就需要建立多个支持向量机。通常情况下，比较典型的方法是“一对多”策略，即需要构造的支持向量机分类器的个数等于状态类型个数，这样一个支持向量机分类器才能够将每一类与余下的各类别的状态区分开来。在机械故障状态识别中，类型的个数不会太多，因此笔者选择该“一对多”策略进行设备的状态识别。

对于某故障训练样本(x1,y1),…,(xl,yl),其中：xi∈Rn;yi∈{-1,1}；l为总样本数；n为特征参数总数。设轴承故障种类数为m，则建立SVM故障识别模型的步骤如下。

1) 对数据做归一化处理，从而消除量纲的影响。调整yi，若故障类别属于第q类，则yqi=1，否则yqi=-1。

2) 建立支持向量机故障分类器，选择合适的惩罚参数C和核函数，并利用训练样本求解最优分类函数。若(xi,yi)为训练样本，其超平面方程为

wTx+b=0

(8)

其中：w为可调权值向量；b为偏值。

其优化问题可描述为在约束条件下

yi(wTxi+b)≥1 (i=1,2,…,n)

(9)

求取Φ(w)=wTw/2

(10)

的最小值问题。

该最小值问题可以利用Lagrange乘子方法将其转化为在以下约束条件下

求取

(13)

的最大值问题。

(14)

在支持向量机中，核函数起了非常重要的作用。若φ(x)表示为输入向量x在特征空间所映射的“像”，则核函数表示为K(xi,xj)=φT(xi)φ(xj)。依据泛函数的相关理论，只要核函数满足Mercer条件，它就能对应某一变换空间的内积。相比线性可分模式，则约束条件式(12)可变为

0≤αi≤C(i=1,2,…,n)

(15)

最优分类函数则变为

(16)

常用的核函数有：

线性核K(x,xi)=xxi；

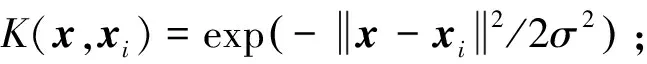
多项式核K(x,xi)=(xxi+1)d(d=1,2,…)；

感知器核K(x,xi)=tanh(βxTxi+b)。

笔者选取的核函数为多项式核函数，进而得到第q类故障的识别模型为

(17)

重复步骤2直到得到m个故障分类模型，利用得到的识别模型，根据特征参数输入模型，进而进行故障类型识别。

4 实例分析

4.1 实例分析一

实验数据一所采用的数据来自网络，故障实验是在特伦顿州NAWCAD直升机传动设备上进行的，数据采集于SH-60直升机的中级齿轮箱。图5所示为该齿轮箱的结构简图，其输入端齿数为25，输出端齿数为30，加速度传感器分别安装在输入端和输出端。该实验模拟齿轮疲劳弯曲断裂，使用电火花在输入端齿轮上加工出痕迹，然后在满载荷下运行至齿轮失效。该网站提供了3组输入输出数据，分别为第7组、第21组以及第34组。笔者所采用的数据为输入端数据，每组数据代表不同程度裂纹故障，分别为轻度裂纹、中度裂纹及重度裂纹。将每个状态数据划分为40组，每组数据大概6个周期。

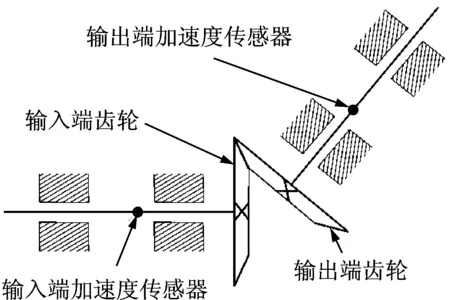
图5 SH-60中级齿轮箱结构简图Fig.5 Structure diagram of the intermediate gearbox on the SH-60 helicopter

对每个状态所提取40组数据进行连续小波变换得到各组数据的时频图像，然后利用Matlab将每组数据的时频图像转换为灰度图并进行非下采样轮廓波变换。分解时非下采样金字塔滤波器选用“maxflat”滤波器，非下采样方向滤波器选用“dmaxflat7”滤波器，由非下采样金字塔分解为2个尺度，非下采样方向滤波器组将得到的高频子带分别分解为4和8个方向。通过以上分解，会得到1个低频子带、第1层的4个方向的高频子带以及第2层的8个方向的高频子带，各子带系数矩阵大小为512×512(M=N=512)的方阵。依据式(2)，(3)，(5)和(6)获取各组特征值，然后取均值作对比。图6所示为这3组不同程度裂纹的特征向量均值，从图中可以看出，随着裂纹程度逐渐增加，各特征均值表现出递增的趋势，>从一定程度上反映了设备的不同状态。

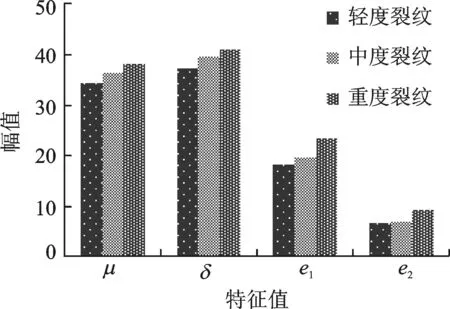
图6 不同裂纹特征向量均值Fig.6 Feature vector mean value of different cracks

将每个状态下取20组数据的特征向量输入到SVM作为训练样本，余下20组数据的特征向量作为测试样本。表1所示为各状态的识别个数，能够看出对于个别轻度裂纹和中度裂纹的识别还不够明确，分类结果有待提高。该结果的分类精度达到96.67%，可见基于小波时频图像和非下采样轮廓波变换的故障特征提取是有效的。

表1 各状态识别个数

4.2 实例分析二

为进一步验证本研究方法的有效性，利用实验室旋转机械振动故障实验平台进行了滚动轴承模拟实验，通过在内环、外环和滚动体上开小槽模拟内环故障、外环故障和滚动体故障，分别测试了正常、内环故障、外环故障以及滚动体故障。利用东方所数据采集软件和NI-9234采集卡进行数据采集，采样频率为10 240 Hz，转速为900 r/min，分别采集了4种不同情况下的振动数据。图7为旋转机械振动故障实验平台，图8为滚动轴承故障类型。图9为不同状态下滚动轴承的连续小波变换时频图，能够看出不同状态下其时频图具有一定的差异，通过笔者提出的方法可进一步描述不同状态间的差异。

图7 旋转机械振动故障实验平台Fig.7 Rotating machinery vibration failure test platform

图8 滚动轴承故障类型Fig.8 Rolling bearing fault type

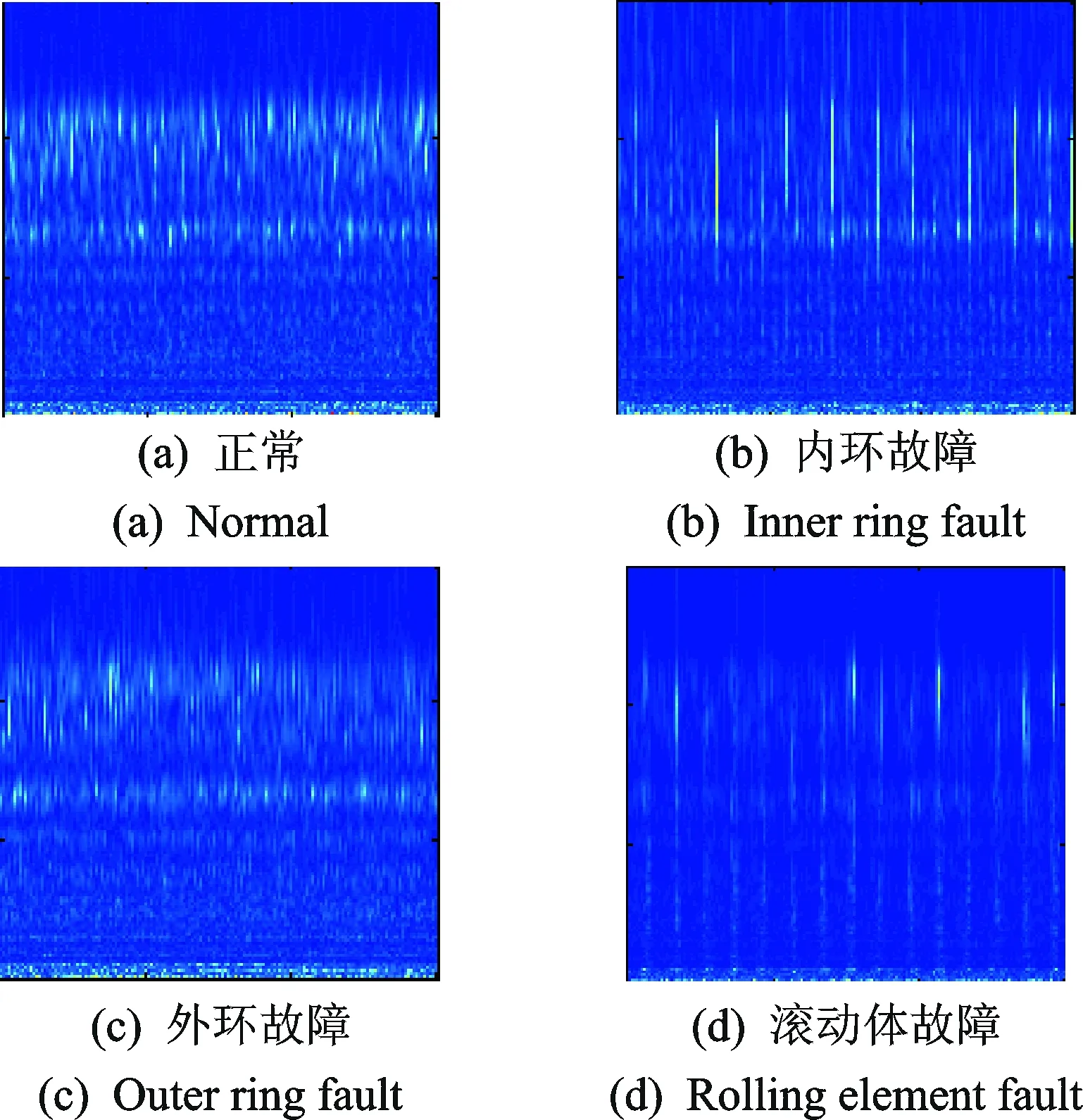
图9 滚动轴承时频图Fig.9 Rolling bearing time-frequency distribution

将所采集的每个状态的数据等时间间隔分为60组，对每组数据进行连续小波变换得到各组数据的时频图像，然后利用Matlab将每组数据的时频图像转换为灰度图并按照实例分析一中参数设定进行非下采样轮廓波变换，进而得到各组特征向量，然后取均值作对比。图10所示为4种不同状态的特征向量均值，从图中看出不同状态某一特征值具有一定的趋势差别。

取其中30组特征向量作为训练样本输入到SVM，余下30组特征向量作为测试样本。表2所示为滚动轴承各不同状态识别个数，该分类结果的精度为95.83%，进一步验证了基于小波时频图像和非下采样轮廓波变换的故障特征提取是有效的。

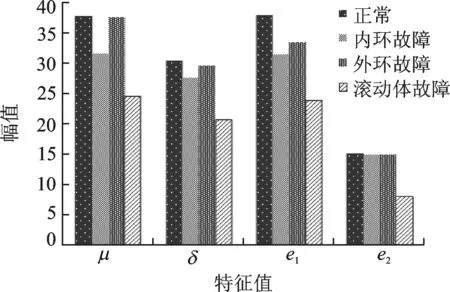
图10 不同状态特征向量均值Fig.10 Feature vector mean value under different status

表2 滚动轴承各状态识别个数

5 结束语

笔者探索了基于非下采样轮廓波变换的图像处理与模式识别的故障诊断方法，分别以齿轮箱和轴承为例展开分析。从可以表征故障特征的非下采样轮廓波变换各子带系数提取4个特征统计量，采用SVM的分类方法进行训练、分类，取得了比较好的识别效果。所提出的方法将有助于基于时频分析的设备故障诊断方法研究与应用。

参 考 文 献

[1] 郑海波，李志远，陈心昭. 基于时频分布的发动机异响特征分析及故障诊断研究[J]. 内燃机学报，2002, 20(3): 267-272.

Zheng Haibo, Li Zhiyuan, Chen Xinshao. Analysis and fault diagnosis of engine abnormal sound based on time frequency distribution[J]. Transactions of CSICE, 2002, 20(3): 267-272. (in Chinese)

[2] 张梅军，唐建，陈江海，等. 基于连续小波灰度图的变速箱故障诊断[J]. 振动、测试与诊断，2007，27(1): 65-67.

Zhang Meijun, Tang Jian, Chen Jianghai, et al. Fault diagnosis of gearbox based on continuous wavelet transform[J]. Journal of Vibration, Measurement & Diagnosis, 2007，27(1): 65-67. (in Chinese)

[3] Renata K, Eyal M, Eduard R, et al. Bearing diagnostics using image processing methods[J]. Mechanical Systems and Signal Processing, 2014 (45): 105-113.

[4] Wang W J, Mcfadden P D. Early detection of gear failure by vibration analysis—ii: interpretation of the time frequency distribution using image processing techniques[J]. Mechanical Systems and Signal Processing, 1993, 7(3): 205-215.

[5] 章立军，刘博，张彬，等. 基于时频图像融合的轴承性能退化特征提取方法[J]. 机械工程学报，2013, 49(22): 53-58.

Zhang Lijun, Liu Bo, Zhang Bin, et al. Feature extraction mechod of bearing performance degradation based on time-frequency image fusion[J]. Journal of Mechanical Engineering, 2013, 49(22): 53-58. (in Chinese)

[6] 吕琛，王桂增. 基于时频域模型的噪声故障诊断[J]. 振动与冲击，2005, 24(2): 54-57.

Lü Chen, Wang Guizeng. Noise fault diagnosis based on time-frequency domain model[J]. Journal of Vibration and Shock, 2005, 24(2): 54-57. (in Chinese)

[7] Do M N, Vetterli M. Contourlet: a new directional multiresolution image representation[C]∥36th Asilomar Conference on signal, Systems and Computers. Pacific Grove,CA:[s.n.], 2002: 497-501.

[8] Do M N, Vetterli M. The contourlet transform: an efficient directional multiresolution image representation[J]. IEEE Trasactions on Image Processing, 2005,14(12): 2091-2106.

[9] 王常青. 数字图象处理分析及其在故障诊断中的应用研究[D]. 武汉：华中科技大学，2012.

[10] 贾函龙，王金芳，黄利飞. 基于非下采样Contourlet变换的人脸表情识别算法研究[J]. 智能计算机与应用，2015, 5(5): 35-39.

Jia Hanlong, Wang Jinfang, Huang Lifei. Facial expression recognition based on the next sampling contourlet transform algorithm research[J]. Intelligent Computer and Applications, 2015, 5(5): 35-39. (in Chinese)

[11] 崔克彬，李宝树，徐雪涛，等. 基于图像增强技术的电气设备热故障自动诊断与定位[J]. 红外技术，2014, 36(2): 162-167.

Cui Kebin, Li Baoshu, Xu Xuetao, et al. Automatic diagnosis and positioning of electrical equipment thermal faults based on image enhancement technology[J]. Infrared Technology, 2014, 36(2): 162-167. (in Chinese)

[12] 董建华，顾汉明，张星. 几种时频分析方法的比较及应用[J]. 工程地球物理学报，2007, 4(4): 312-316.

Dong Jianhua, Gu Hanming, Zhang Xing. A comparison of time-frequency analysis methods and their applications[J]. Chinese Journal of Engineering Geophysics, 2007, 4(4): 312-316. (in Chinese)

[13] 周新星，王典洪，王洪亮，等. 基于非下采样Contourlet变换和PCNN的表面缺陷自动识别方法[J]. 应用基础与工程科学学报，2013, 21(1): 174-183.

Zhou Xinxing, Wang Dianhong, Wang Hongliang, et al. Automatic recognition method of surface defects based on non-subsampled contourlet transform and PCNN[J]. Journal of Basic Science and Engineering, 2013, 21(1): 174-183. (in Chinese)

[14] Arthur L, Da Cunha, Zhou Jianping. The non-subsampled contourlet transform: theory, design, and applications[J]. IEEE Transactions on Image Processing, 2005, 15(10): 3089-3101.

[15] 王凯，张永祥，李军. 基于支持向量机的齿轮故障诊断方法研究[J]. 振动与冲击，2006, 25(6): 97-99.

Wang Kai, Zhang Yongxiang, Li Jun. Reasearch on gear fault diagnosis method based on support vector machine[J]. Journal of Vibration and Shock, 2006, 25(6): 97-99. (in Chinese)