多硬度拼接淬硬钢铣削动力学分析*
2018-08-01岳彩旭高海宁张海涛刘献礼
岳彩旭, 冯 磊, 高海宁, 朱 磊, 张海涛, 刘献礼
(哈尔滨理工大学机械动力工程学院 哈尔滨,150080)
引 言
在大型汽车覆盖件冲压过程中,由于局部结构承受较型面更高的挤压应力,容易出现磨损严重、拉毛拉裂等问题[1]。为提高汽车覆盖件模具的使用寿命,需要根据不同部位受力、受热特征采用不同硬度的拼接工件来提升加工效率[2]。由于拼接工件硬度差的影响,致使铣削拼接过缝处时铣削力幅值明显变化且加剧了振动,进而降低工件表面质量和刀具的使用寿命。由于淬硬钢材料硬度较高,会对铣削过程切削力幅值有显著影响。在铣削多硬度拼接淬硬钢的过程中,刀具与工件挤压接触时硬度瞬时变化,导致铣削拼接工作时的振动规律较单一硬度条件更复杂,难于控制。在铣削系统动力学建模方面,诸多学者对此进行了研究。Altintas等[3-4]针对铣削稳定性问题展开了一系列研究工作,建立了多自由度动力学模型,通过仿真得到铣削稳定性曲线,所建立的稳定性预测方法为后续工作提供有利的理论根据。梁睿君等[5]建立稳定性模型,根据刀具和工件之间的动态特性绘制出的稳定性叶瓣图比单独考虑刀具系统绘制出的稳定性曲线更为准确,并用铣削试验验证了铣削叶瓣图的正确性。马海真等[6]通过高速铣削动力学研究,提出了控制模具型面切削过程稳定性的方法,目的是为了针对多硬度拼接淬硬钢稳定性提供可靠的理论。
对于单一硬度稳定性预测也有大量研究, Li等[7]运用时域预测方法得到了铣削稳定性曲线。Tang等[8]采用模态分析方法预测了45号钢的颤振情况来预测极限切深。Budak等[9]研究了铣削稳定状态下的最大切削深度,得到了主轴转速和轴向切削深度函数关系的稳定性曲线。Kong等[10]采取模糊数学方法分析了铣削稳定性极限切削深度,绘制出铣削稳定性区域,得到优化工艺参数的方法。Stori等[11]根据轴向切削深度和主轴转速的关系来研究铣削稳定性影响因素,得到了影响稳定性因素的主次关系,并优化了工艺参数。黄鹏等[12]基于颤振机理研究了TC4钛合金高速加工过程中的切削稳定性问题。Yan等[13]针对变切削深度对车削稳定性进行了研究。Schmitz等[14]通过子结构分析法研究了刀具悬伸长度变化对稳定性预测曲线的影响规律,其目的是获得最大材料切除率。Weingaertner等[15]进行铣削试验,测试铣削加工过程中不同音频波形图,得到试验数据,最后建立稳定性叶瓣图,验证了铝合金加工过程的稳定性。宋清华等[16]采取半离散方法对铣削稳定性预测曲线和工件表面质量的关系进行了深入探讨,分析了共振区与稳定区域的位置关系,并通过试验验证了稳定性预测曲线的稳定性。李忠群等[17]采用频响函数的方法建立铣削稳定域曲线,采取多模态分析法仿真薄壁件铣削稳定性曲线。杨建中[18]建立了二维动力学模型,推导了主轴转速与切削深度变化关系公式,通过仿真得出动刚度最小的模态决定了叶瓣图的主要形状。迟玉伦等[19]的研究将理论模型与试验设计相结合,建立的铣削颤振稳定域叶瓣图在机床实际铣削加工过程中得到有效应用。
诸多学者对铣削稳定性分析已有大量研究,但在铣削拼接模具过程(从低硬度工件到高硬度工件铣削过程)中,由于硬度差的影响使得铣削拼接过缝区域时产生突变,加剧了振动,不仅对铣削系统稳定性产生影响,而且会导致刀具磨损加剧及工件表面质量降低。连续铣削不同硬度工件时的铣削力也是不同的,工件的硬度差造成颤振的加剧。因此,实现拼接模具的稳定性预测能为多硬度拼接淬硬钢铣削加工提供合理的加工参数,实现材料的最大切除率。笔者提出了多硬度拼接淬硬钢铣削过程的稳定性预测模型,得到在铣削不同硬度工件下的颤振稳定域,并进行了试验验证,获取了铣削拼接模具过程的振动加速度信号以及刀具磨损状况和工件表面质量。综合分析验证了多硬度拼接淬硬钢铣削稳定性预测模型的准确性。
1 铣削系统动力学建模
全离散的稳定性预测方法不仅得到了铣削试验的广泛验证,而且已经被扩展应用到了球头铣削曲面工件的稳定性研究中,笔者将全离散法应用到多硬度拼接工件铣削系统动力学建模中。
首先建立了x,y方向的二自由度铣削系统的时滞微分方程,表达式为
(1)
其中:ωnx,ζx,kx,ωny,ζy,ky分别为x,y方向上的固有频率、阻尼比、刚度系数;ap为轴向切削厚度;Kt为切向的切削力系数;T为刀齿通过周期;x(t-T)和y(t-T)为时滞项。
时变方向系数表示为
(2)
其中:N为球头铣刀齿数;Kr为径向与切向铣削力系数的比值;φj(t)为铣刀第j齿的位置接触角。
φj(t)可表示为
φj(t)=(2πΩ/60)t+2π(j-1)/N
(3)
其中:Ω为主轴转速,单位为r/min;g(φj(t))为判断刀齿j是否参与切削的函数。
g(φj(t))被定义为
(4)
其中:φst和φex分别为刀齿j铣削过程的切入角和切出角。
逆铣时,φst=0且φex=arc cos(1-2aε/D);顺铣时,φst=arc cos(2ae/D-1)且φex=π,ae/D表示径向浸入率(ae为径向切削深度;D为球头铣刀的直径)。
2 铣削稳定性预测算法分析
由于铣削力是各个铣削离散微元组合而成,不能通过简单的解析计算方法来求解,因此采用数值解法对动态铣削过程进行仿真。在求解常系数非齐次方程时,重点是采用离散化的数学解法将时间区间分成不同时间点,再将各个离散点的近似值作为方程解。使用经典四阶龙格库塔迭代方法来求解动态位移,最后,通过Floquet理论判断传递矩阵特征方程根来预测铣削过程的稳定性。此方法较其他方法有更高的收敛率、计算精度及计算效率。本研究采用的是由李忠群等[20]提出的基于四阶龙格库塔方法的全离散法,步骤如下:
1) 将动力学微分方程改写成方程左侧只有振动加速度一项的表达式;
2) 将时间离散化,并假定初始条件t=t0时,x(t0)=y(t0)=0,x′(t0)=y′(t0)=0;
3) 令时间周期t=t0+idt(i= 1,2,… ),对动力学微分方程进行求解。
通过转换式(1)到空间形式表示为

(5)
其中:A(t)和B(t)为时间周期系数矩阵。
由于此矩阵受到动态切削力(再生效应)的影响,则A(t)=A(t+T),B(t)=B(t+T),T为时间周期。T此时不仅表示该铣削系统时间周期,而且T的数值与时滞量相等。τ为时滞时间,在T=τ时为单延迟铣削过程。
为了计算式(5),本节使用四阶龙格库塔方法,时间周期T等距离散成m个时间段(m为整数),每段时间间隔为Δt,T=mΔt,m也等于单齿通过周期的离散数,由龙格库塔迭代法可以将方程表示成
(6)
其中:ui表示u(iΔt);ui+1表示u[(i+1)Δt];ti表示idt,变量i为整数且满足0≤i≤m。
公式依次推导得
(7)
将式(7)代入到式(6)中,得到ut的迭代公式为
ut+1=Fiui+Fi-mui-m+Fi-m+1ui-m+1
(8)
式(8)中系数Fi,Fi-m,Fi-m+1表示为
(9)
其中:I为n×n单位矩阵;n为矢量ut的维数。
为了获得传递矩阵,通过上述变量,定义一个新的n×(m+1)维度的矢量公式为
zi=col(ui,ui-1,…,ui-m+1,ui-m)
(10)
其中:col函数表示呈列向量分布。
构建出单个时间周期内的过度矩阵为
zi+1=Dizi
(11)
传递矩阵φ表示为
φ=Dk-1Dk-2…D2D1
(12)
根据Floquet理论,如果传递矩阵φ的特征方程根的模大于1,则系统不稳定;否则系统是稳定的。因此,边界曲线在稳定性图表中被分为稳定区域和不稳定区域,进而得到判定是否发生颤振的依据。
3 多硬度拼接淬硬钢铣削稳定性分析
通过特定刀具、工件材料和径向接触角,可求得平均方向系数,然后按照如下步骤获取颤振稳定叶瓣图:
1) 设置固定参数,如铣削系统模态参数、刀具几何参数、切削参数等;
2) 将周期T离散成m个;
3) 计算4个切削力方向系数;
4) 定义系数矩阵;
5) 计算时间周期系数矩阵;
6) 求解传递系数矩阵并求得特征方程根;

图1 多硬度拼接淬硬钢铣削稳定性仿真流程图Fig.1 Stability lobes simulation chart of milling multi-hardness mosaic hardened steel
7) 根据Floquet矩阵判断系统是否稳定,流程图如图1所示,其中,eig(Φ)为求解传递函数的全部特征值,abs(eig(Φ))为求解全部特征值的模,最后把传递函数模的最大值赋给变量Tag,此处Tag代指传递函数特征值模的矩阵。
3.1 铣削力系数识别
铣削力系数辨识试验是利用在铣削试验过程中在一定的切削参数下得到三向铣削力的平均值,然后根据铣削力建模得到的铣削力系数公式,从而得到工件的铣削力系数。图2和图3为试验所用的机床设备和原理图。试验测试所需主要硬件包括Kister9257B测力平台、Kistler5070A电荷放大器、电脑和试件,数据采集分析系统为DH5922数采系统,试验所用刀具是齿数为2的硬质合金球头铣刀,工件材料为Cr12MoV淬硬钢,其硬度为60HRC和45HRC。根据斜面槽切试验来获得铣削力系数,将试验测得铣削力试验数据代入到铣平均削力系数计算公式中,可以计算得到不同硬度下的铣削力系数,如表1所示。

图2 铣削试验所用机床与设备Fig.2 Machines and equipment of milling test

图3 试验加工测量现场原理图Fig.3 Schematic diagram of experimental measurement

表1 HRC45和HRC60的铣削力系数
工件硬度的改变会影响铣削力系数,在同等材料下硬度越大铣削系数越大,增大趋势呈非线性增大。所得不同硬度下的铣削力系数将为后期稳定性预测曲线的编程提供参数基础。
3.2 铣削系统模态参数识别
笔者采用力锤击法锤击刀杆上标注好的排列点,针对轴向进行均匀测试点分布,并选择第10个排列分布点为拾振点,其余点都为激振点。一次敲击后获取多个瞬态激励信号和频率响应函数,并通过模态识别得到模态参数。模态试验的原理如图4所示,试验需要用到的设备和仪器主要包括东华脉冲测力锤、PCB加速度传感器、DH5922数据采集分析系统及主机等。

图4 模态试验原理图Fig. 4 Schematic diagram of modal test
通过锤击试验得到的铣削系统模态参数如表2所示。

表2 刀具-工件系统的模态参数
3.3 稳定性分析
从HRC45工件铣削到HRC60工件的加工过程,由于两种工件硬度的不同导致两个阶段的铣削力系数也不同,因此对稳定性预测曲线会产生影响。铣削过程中,当工件硬度逐次增大,对应的铣削力系数Kr和Kt同时增大。在相同动力学参数和切削条件下,不同工件硬度(HRC45,HRC60)淬硬钢铣削稳定性叶瓣图如图5所示。由图5可知,铣削工件硬度不同会产生不同的稳定性曲线。硬度越大,铣削极限轴向切削深度越小,且随着主轴转速的提高,两稳定性极限曲线差值逐渐增大,尤其是在每一叶瓣图最高点位置。
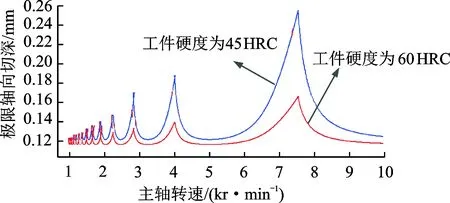
图5 多硬度拼接淬硬钢铣削稳定性预测曲线图Fig.5 Stability lobes of milling multi-hardness mosaic hardened steel
由于加工多硬度拼接淬硬钢时是连续的铣削过程,切削参数的设置不变,为了保证工件的加工精度以及避免颤振的发生,要选取稳定区域内的切削参数来保证铣削加工过程的稳定性。在图5的稳定性预测曲线中,选择2条曲线包络位置中间的区域为临界稳定性区域。利用笔者提出的稳定性预测曲线时,在由高硬度切向低硬度材料时,切削参数可以选择2条稳定性叶瓣图之间的参数,当由低硬度切向高硬度材料时必须选择高硬度稳定性预测曲线以下参数。
4 模态参数对拼接模具铣削稳定性预测曲线的影响分析
在实际铣削加工过程中,根据铣削稳定性预测模型可知,不仅切削参数与刀具几何参数会影响稳定性预测曲线,其他因素也同样会影响铣削稳定性,比如刀具偏心、机床-刀具模态参数(包括固有频率ωn、刚度系数k,阻尼比ε)及结构阻尼等。可以分析以上几种因素对铣削系统稳定性的影响,通过改变切削条件来避免颤振的发生。
在保持刀具参数、切削参数及其他两个模态参数影响因素不变前提下,分别改变一个模态参数影响因素来分析对铣削稳定性预测曲线的影响情况
4.1 固有频率对铣削稳定性预测曲线的影响
由理论可知,固有频率的改变会影响稳定性预测曲线。映射在稳定性预测曲线上的特征主要是影响由主轴转速和切削深度绘制的平面位置图。在保持其他参数不变的情况下,只改变固有频率来观察稳定性预测曲线变化趋势。
从铣削淬硬钢稳定性叶瓣图可以看出,随着固有频率的提高,铣削系统稳定性区域逐渐增大。为了避免颤振的发生,可以改变刀具的参数,比如增大铣刀直径,尽量选择悬伸量小的刀具,来提高铣削系统稳定性。
假定铣削系统中x,y方向模态参数近似相同,阻尼比ε=0.02,刚度k=7.5×106N/m。在其他参数不变的情况下,分别取ωn1=400Hz,ωn2=600Hz,ωn3=800Hz进行仿真,得到的叶瓣图如图6所示。当固有频率增大时,稳定性预测曲线会沿着横坐标右移,对应最大稳定区域的主轴转速增大,但临界切深没有明显变化。
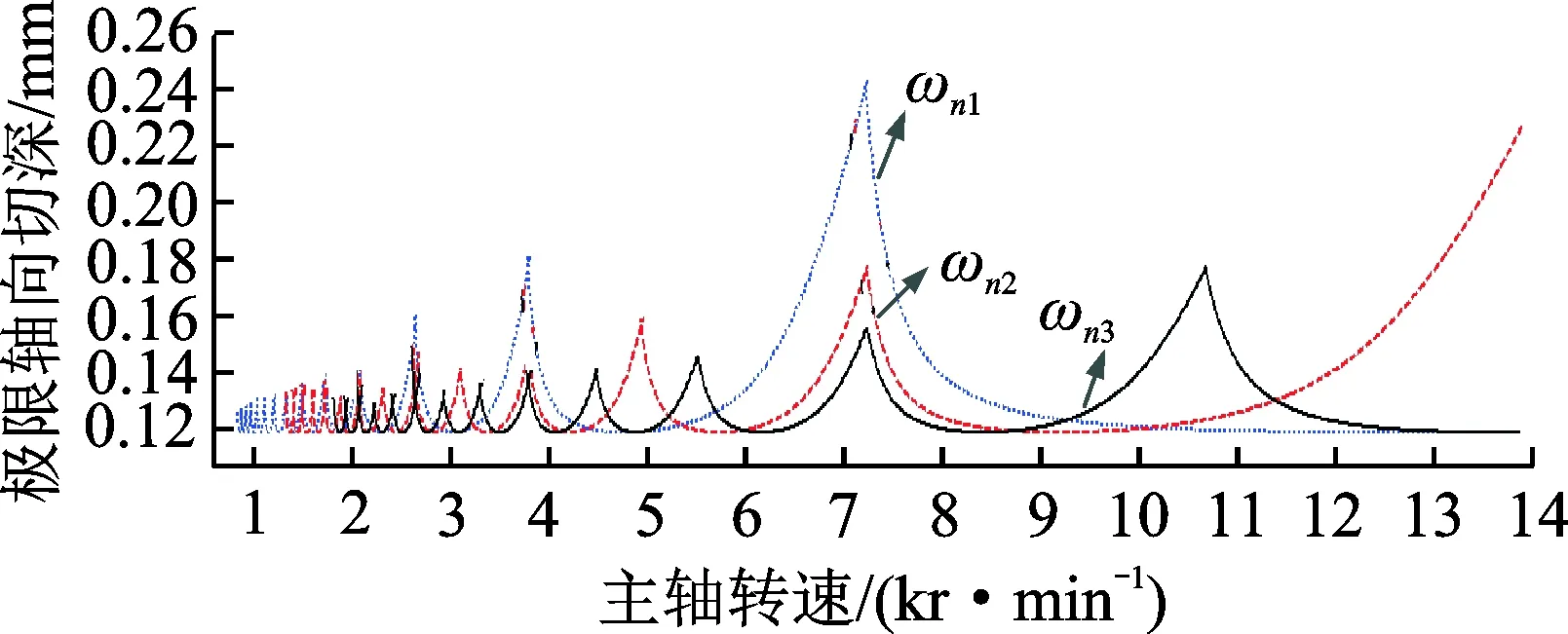
图6 固有频率对铣削稳定性预测曲线的影响Fig.6 The influence of natural frequencies on stability lobes
4.2 阻尼比对铣削稳定性预测曲线的影响
阻尼比是动态特性研究中的重要参数,振动过程中阻尼衰减的程度会影响铣削系统的稳定性。保持其他切削参数与刀具参数不变的前提下,刚度k=7.5×106N/m,ωn=800Hz,阻尼比ε=0.02。改变x,y向阻尼比,分别采用给定阻尼比的倍数(1,2,3倍)进行Matlab仿真,结果见图7。可以观察到随着阻尼比的增大,稳定预测曲线波谷的幅值沿着纵向逐渐增大,临界切深也逐渐增大,但在横向上并没有明显变化,铣削稳定曲线包络区域变大。

图7 阻尼比对铣削稳定性预测曲线的影响Fig.7 The influence of damping ratio on stability lobes
4.3 模态刚度对铣削稳定性预测曲线的影响
保持铣削系统的切削条件、切削参数、刀具参数、固有频率和阻尼比不变,当刚度k=7.5×106N/m,ωn=800Hz,阻尼比ε=0.02,同时改变x,y向的模态刚度参数,采取铣削系统模态刚度值的倍数(1,2,3倍)进行仿真,结果如图8所示。从图中可以观察到,随着模态刚度的提升,临界轴向切削深度逐渐增大,曲线整体上移,在横线没有明显变化,故模态刚度的提升可以增强铣削系统的稳定性。

图8 模态刚度对铣削稳定性预测曲线的影响Fig.8 The influence of modal stiffness on stability lobes
5 铣削稳定性预测结果验证
在仿真稳定性预测曲线过程中,选取适当的主轴转速与切深,主轴转速的选取范围在2kr/min~8kr/min之间,步长为1kr/min,切削深度选取0.12,0.13,0.14 mm。铣削验证试验采用奥地利EMCO公司生产的三轴数控铣床。
在多硬度拼接模具加工试验中,保持每齿进给量不变,设定不同的主轴转速与轴向切深,采用干式切削方式加工。利用DH5922的信号采集系统导出铣削力信号以及振动加速度信号,通过对比铣削力、振动加速度幅值变化来判断是否发生颤振。
多硬度拼接淬硬钢铣削过程稳定性预测结果如图9所示。为了验证多硬度拼接淬硬钢球头铣削稳定性预测曲线的预测精度,保持进给速度800mm/min不变,提取铣削稳定性叶瓣图中的局部点如A点(n=4kr/min,ap=0.12mm),B点(n=5kr/min,ap=0.12mm),C点(n=4kr/min,ap=0.14mm),D点(n=5kr/min,ap=0.14mm),E点(n=5kr/min,ap=0.13mm),F点(n=6kr/min,ap=0.13mm)对应切削参数下的铣削振动加速度信号进行试验分析。
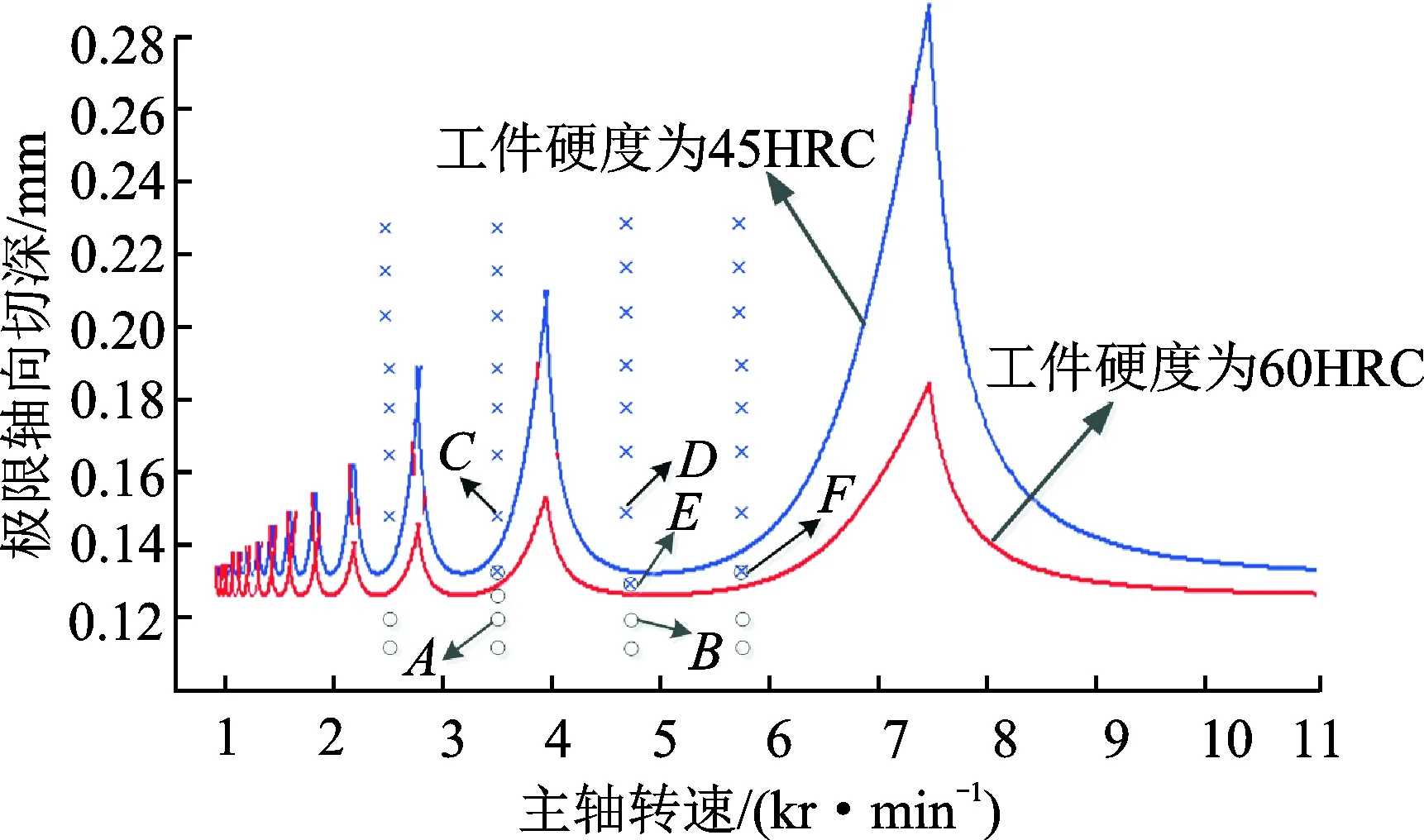
图9 铣削加工试验结果Fig.9 Experimental result of milling process
图10 (a),(b),(c)分别对应A点、B点和C点切削参数,由图可以看出:A和B点振动加速度信号保持平稳状态,加速度波动范围在5 m/s2以内,在试验过程中没有听到刺耳的声音,因此综合可以确定A和B点都处于稳定区域内,与预测结果一致;C点的加速度信号波动程度较A,B两点更剧烈,球头铣刀铣削拼接淬硬钢过程中,在铣削两个硬度的阶段都呈现不稳定的切削状态,振动加速度信号都在15 m/s2左右,刀具与工件振动剧烈,并产生极大的噪音,所以综合可以判断C点处于不稳定区域。
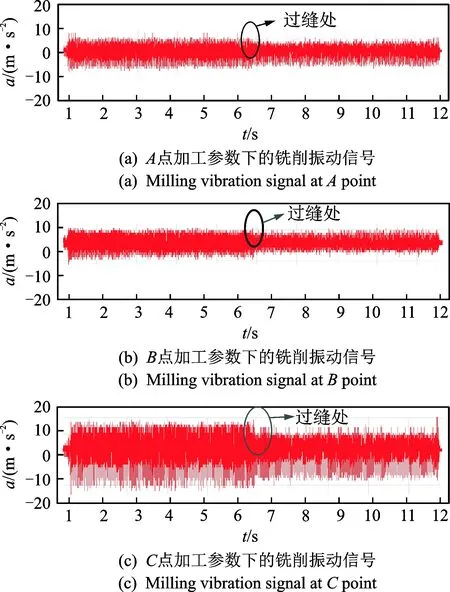
图10 第1组数据的试验结果Fig.10 Result of the first group data
图11中(a),(b),(c)分别对应D点、E点和F点的振动加速度信号,从E点的加速度信号可以看出,球头铣刀在铣削高硬度淬硬钢区域时振动较低硬度更剧烈,加速度幅值在8 m/s2左右,而铣削低硬度淬硬钢时振动信号较为平稳,加速度信号幅值在5 m/s2内波动,与稳定性叶瓣图的结果吻合。D和E点是在相同转速、不同切深条件下的两点,从D点的加速度信号图可以看出,在铣削两个硬度的阶段都呈现不稳定的状态,振动加速度信号都在15 m/s2左右,刀具与工件振动剧烈,产生极大的噪音,所以判断D点处于不稳定区域。F点是与E点在同一切深、不同主轴转速下的的铣削振动信号,可以看出F点切削参数条件下,在铣削高硬度区域时振动较剧烈,加速度幅值在8 m/s2左右,而铣削低硬度淬硬钢时振动信号较为平稳,加速度信号在5 m/s2内波动,与预测结果一致。
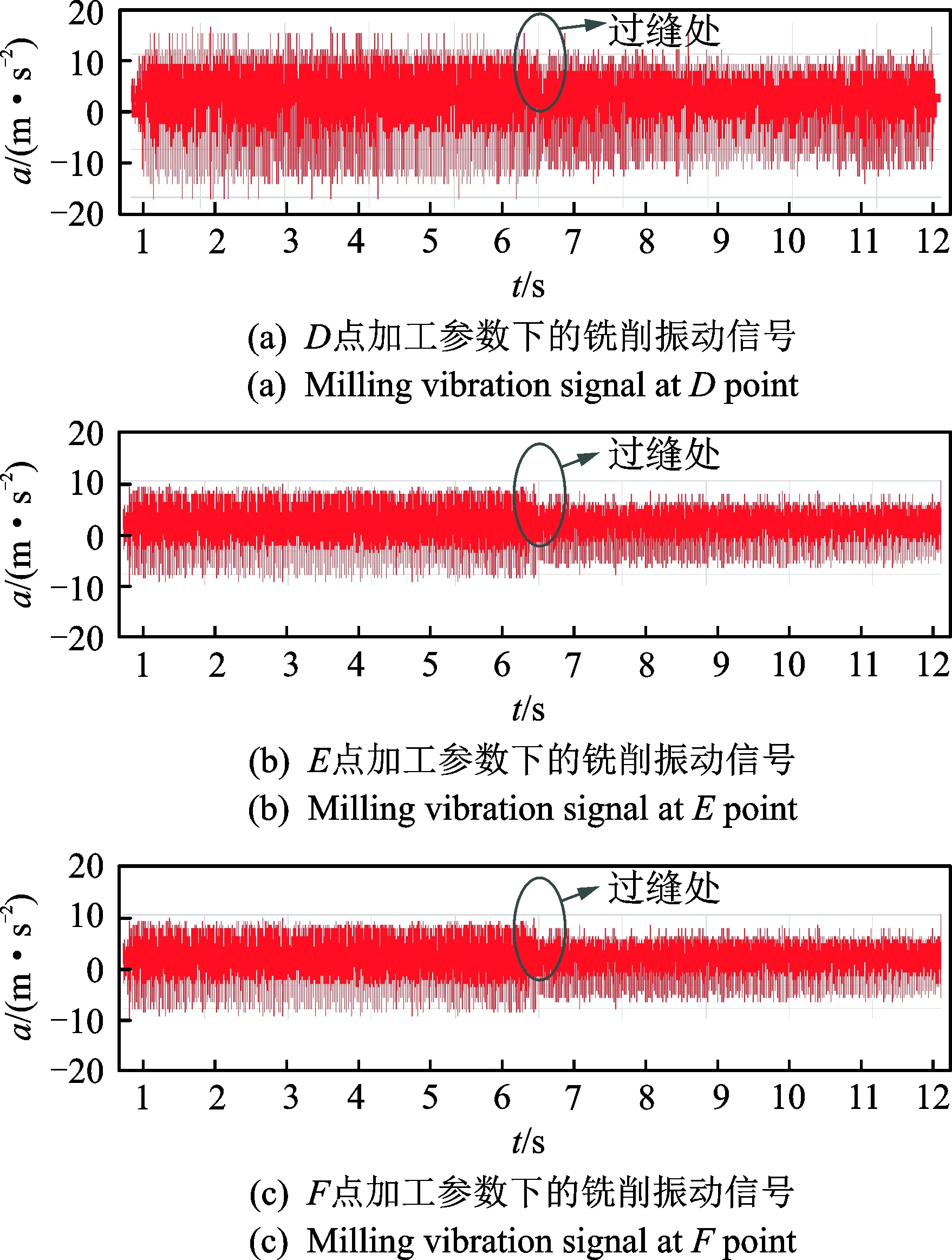
图11 第2组数据的试验结果Fig.11 Result of the second group data
根据稳定性预测曲线选取的局部点A,B,C,D,E和F的试验结果可知,试验结果和仿真出的铣削叶瓣图基本一致,精度较高,说明笔者绘制的多硬度拼接淬硬钢铣削稳定性预测曲线是准确的。
6 多硬度拼接淬硬钢铣削刀具磨损和表面形貌验证
工艺参数优化是对特定的机床、刀具和工件的切削参数进行多方面的研究,来得到使铣削力突变小、铣削过程稳定、表面精度高和刀具磨损小的切削用量。在连续铣削加工多硬度拼接淬硬钢时,由于刀具和工件接触区出现了硬度偏差而引起铣削力突变,进而加剧振动,影响工件的表面质量和刀具磨损,利用这两种表征进行多硬度拼接模具铣削稳定性的验证分析。
选取上述试验的铣削参数进行表面形貌与刀具磨损的验证,即保持进给速度800mm/min不变,提取铣削稳定性叶瓣图中A,B,C,D,E和F点对应此切削用量下的表面形貌和刀具磨损情况进行分析。试验结果采用超景深显微镜测量表面形貌和刀具磨损,得到如图12,13所示结果。

图12 第1组数据表面形貌和刀具磨损情况Fig.12 Tool wear and surface topography of the first group data
如图12所示,在A点测量三点平均磨损量为6.37μm,从图(a)刀具形貌和磨损量的数值可以看出,刀具只发生轻微的磨损,故A点切削参数条件是稳定切削。在B点测量的三点平均磨损量为5.57μm,由图(b)可以看出,刀具磨损的程度很小,且较A点的磨损量更小,所以B点切削参数条件下也是稳定切削。在C点测量的三点平均磨损量为92.97μm,由图(c)可以看出,刀具发生强烈的磨损,C点磨损值是A点磨损值的15倍,磨损量较大且刀具发生崩刃,故C点切削参数条件是不稳定切削。从表面形貌来看,A和B点参数条件下,表面凹坑排布规则,两种硬度表面形貌都较好;C点的表面凹坑排布不规则,靠近拼接缝时,凹坑排布更集中,HRC60的工件比HRC45的表面形貌好,即C点处于不稳定区域。

图13 第2组表面粗糙度和刀具磨损情况Fig.13 Tool wear and surface topography of the second group data
如图13所示,在D点测量三点平均磨损量为69.6μm,刀具发生强烈的磨损且发生崩刃,而且磨损数值较相同转速不同切深条件下的B点增大了10倍,综合可以得出D点切削参数条件是不稳定切削。在E点测量两点平均磨损量为29.7μm,E点的切深在B,D两点切深之间,E点刀具磨损值也介于两者磨损值之间,但磨损值与切削深度并非简单的线性关系,综合以上可以得出E点切削参数条件是处于稳定切削和不稳定切削之间的介稳切削过程。在F点测量的三点平均磨损量为25.93μm,刀具发生了较剧烈的磨损,磨损值与E点的磨损值相近,因为在稳定性叶瓣图中E,F在相同的区域,切削深度接近且两点都靠近稳定性临界曲线,但从两点的切削力数值来分析,不同主轴转速条件下,E点切削力数值大于F点的数值,综合以上可以得出F点切削参数条件也是处在稳定切削和不稳定切削之间的介稳切削过程。从表面形貌来看,D点参数条件下,表面凹坑排布分散,表面质量差,靠近拼接缝时,凹坑排布更集中,HRC60的工件比HRC45的表面形貌好;E和F点表面形貌相似,凹坑分布较C和D两点均匀。
将上述结果加入到稳定性预测曲线中,可以更直观地看出选取局部6个数据点的稳定情况如图14所示。
从测量的表面形貌和刀具磨损对应铣削稳定性叶瓣图可知,铣削稳定下的切削用量能得到高的表面质量,并降低了刀具磨损程度;然而在不稳定参数条件下,表面质量严重下降且刀具磨损较大,甚至会导致刀刃破损,从而验证了铣削稳定性叶瓣图的正确性。

图14 稳定性叶瓣图中表面形貌和刀具磨损Fig.14 Tool wear and surface topography in the stability lobes
7 结 论
1) 通过试验结果可知,稳定性预测曲线上、下两区域分别为不稳定区域和稳定区域。试验结果与预测曲线吻合,验证了提出的预测模型的准确性。
2) 材料硬度大小、固有频率、阻尼比和模态刚度影响铣削加工稳定系统,铣削高硬度的稳定性区域较低硬度区域要小。随着固有频率增大,稳定性预测曲线向右移动,阻尼比的增大致使预测线曲波谷幅值大幅度提升,增大刚度致使曲线临界切深变大,并增大稳定性。
3) 通过时域分析、表面形貌和刀具磨损分析,综合验证了本研究提出的预测模型的正确性。在不稳定区域的工艺参数会降低表面质量并加剧刀具磨损,在稳定区域的工艺参数得到高质量表面形貌并降低了刀具磨损。
参 考 文 献
[1] “中国制造业可持续发展战略研究”咨询研究项目组. 中国制造业可持续发展战略研究[M]. 北京:机械工业出版社,2010:120-129.
[2] 向红英.拉延模型面采用镶块拼接的原因分析[J]. 西华大学学报:自然科学版, 2006, 25(3):44-45.
Xiang Hongying. Analysis of using insert splice in drawing model[J]. Xihua University Journals: Natural Science Edition, 2006, 25(3):44-45.(in Chinese)
[4] Altintas Y, Weck M. Chatter stability of metal cutting and grinding[J]. The International Academy for Production Engineering Annals - Manufacturing Technology, 2004, 53(2):619-642.
[5] 梁睿君,叶文华.薄壁零件高速铣削稳定性预测与验证[J]. 机械工程学报, 2009, 45(11):146-151.
Liang Ruijun,Ye Wenhua. Stability prediction and validation in high speed milling thin-walled parts[J].Mechanical Engineering Journal, 2009, 45(11):146-151. (in Chinese)
[6] 马海真,姜彬,郑敏利,等.钼钒铸铁汽车覆盖件模具数控高效切削加工稳定性研究[J]. 工具技术, 2008, 42(8):17-20.
Ma Haizhen,Jiang Bin,Zheng Minli,et al.NC high efficiency cutting stability study on Mo-V cast iron automobile cover mold[J].Technology of Tools, 2008, 42(8):17-20.(in Chinese)
[7] Li Zhongqun, Liu Qiang. Solution and analysis of chatter stability for end milling in the time-domain[J]. Chinese Journal of Aeronautics, 2008, 21(2):169-178.
[8] Tang Weixiao, Song Qinghua, Yu S Q, et al. Prediction of chatter stability in high-speed finishing end milling considering multi-mode dynamics[J]. Journal of Materials Processing Technology, 2009, 209(5):2585-2591.
[9] Budak E, Tekeli A.Maximizing chatter free material removal rate in milling through optimal selection of axial and radial depth of cut pairs[J]. The International Academy for Production Engineering Annals-Manufacturing Technology,2005,54(l):353-356.
[10] Kong Fansen, Yu Junyi. Study of fuzzy stochastic limited cutting width on chatter[J].The International Journal of Advanced Manufacturing Technology,2007,33:677-683.
[11] Stori J,Wright P. Parameter space decomposition for selection of the axial and radial depth of cut in endmilling [J].Journal of Manufacturing Science and Engineering,2001,123:654-664.
[12] 黄鹏,邵芳.高速切削钛合金稳定性模型及极限切深预测[J]. 机械设计与制造, 2016(12):129-131.
Huang Peng, Shao Fang.The stability model of titanium alloy and prediction of limit cutting depth in high speed cutting[J]. Mechanical Design and Manufacture, 2016(12): 129-131.(in Chinese)
[13] Yan Rong,Tang Weixiao,Peng Fangyu, et al. The effect of variable cutting depth and thickness on milling stability for orthogonal turn-milling[J]. The International Journal of Advanced Manufacturing Technology, 2016, 82(1):765-777.
[14] Schmitz T, Couey J, Marsh E,et al. Runout effects in milling: surface finish, surface location error, and stability[J]. International Journal of Machine Tools & Manufacture, 2007, 47(5):841-851.
[15] Weingaertner W, Schroeter R, Polli M L, et al. Evaluation of high-speed end-milling dynamic stability through audio signal measurements[J]. Journal of Materials Processing Technology, 2006, 179(1):133-138.
[16] 宋清华,艾兴,于水清.高速铣削稳定性与表面加工精度研究[J]. 制造技术与机床, 2008(4):40-43.
Song Qinghua,Ai Xin,Yu Shuiqing. Study on high speed milling stability and machining precision[J].Manufacturing Technology and Machine Tools, 2008(4):40-43. (in Chinese)
[17] 李忠群,刘强.基于频响函数的高速铣削颤振稳定域快速分析与研究[J]. 制造技术与机床, 2008(4):53-57.
Li Zhongqun,Liu Qiang. The quick analyses and study of flutter stability religion based on frequency response function in high speed milling[J]. Manufacturing Technology and Machine Tools, 2008(4):53-57. (in Chinese)
[18] 杨建中.铣削加工过程稳定性分析[J]. 中国机械工程学报,2013,24(3):360-365.
Yang Jianzhong.The stability analyses of milling process[J]. Mechanical Engineering Journal, 2013,24(3):360-365.(in Chinese)
[19] 迟玉伦,李郝林.铣削颤振稳定域叶瓣图确定方法研究[J].振动与冲击,2014,33(4):90-93.
Chi Yulun,Li Haolin.Study on the determining method of milling flutter stability lobes[J]. Journal of Vibration and Shock,2014,33(4):90-93.(in Chinese)
[20] Li Zhongqun,Yang Zhikang. Prediction of chatter stability for milling process using Runge-Kutta-based complete discretization method[J]. The Internation Journal of Advanced Manufacturing Technology, 2016, 86:943-952.
