导波强化裂变聚合概率模型损伤监测方法*

邱 雷， 房 芳， 袁慎芳， 梅寒飞

(南京航空航天大学机械结构力学及控制国家重点实验室 南京，210016)

引 言

结构健康监测技术(structural health monitoring，简称SHM)能够在线监测结构健康状态，对结构损伤及剩余寿命进行预测和估计，最终保障飞行器结构安全并降低维护成本[1-2]。近年来，SHM技术已由早期理论研究逐渐转向工程应用研究[3-4]。在众多的SHM技术中，基于导波的SHM技术具有监测面积大、对小损伤敏感等优点[5-7]，是一种很有应用前景的重要SHM技术。

在实际工程应用中，SHM技术要面临相比实验室条件更加复杂的服役环境。随时间变化的温湿度、边界条件、随机振动及疲劳载荷等环境因素会直接影响SHM传感器、监测系统等的输出信号特征[8]，这些影响要比结构损伤对导波信号的影响还要剧烈，使得损伤诊断无法可靠进行。因此，保证时变环境下损伤监测的可靠性是该技术实际应用时的一个重要关键问题。一些学者提出诸如环境因素补偿[9]、监测基准优化[10]等方法，但这些方法在实际应用过程中都存在一定的局限性，如环境因素补偿方法目前仅能对单一温度因素进行补偿，而监测基准优化方法目前只在简单结构上得到验证。由于时变服役环境对信号的影响体现出很强的不确定性和非线性，故有研究在SHM中应用了概率统计模型来应对时变问题的不确定性。

在概率统计模型中， GMM是一种有限混合概率模型，可在无先验知识的前提下通过多个高斯分量的加权组合逼近复杂随机变量的概率分布，被广泛应用于图像分割和语音识别等领域[11]。近年来，有学者将其应用于时变环境影响下的SHM领域中。Banerjee等[12]将其应用于热点问题监测中，并在有温度突变的结构上实现了裂纹扩展监测。Kullaa[13]利用GMM对结构所处环境中非线性因素进行建模，实现温度影响下的桥梁结构健康监测。文献[14]利用在线更新GMM实现飞机大梁边界条件变化下的裂纹监测。这些研究利用GMM实现时变环境下的损伤监测，但大都基于期望最大化(expectation maximization，简称EM)算法训练GMM，而这样的GMM存在的问题限制了实际损伤监测效果。首先，EM算法训练的常规GMM对其初始取值敏感，易使GMM收敛于局部极值[15]，导致训练的GMM存在多种不确定的分布形式，从而影响损伤诊断结果的稳定性；其次，复杂的结构应力分布、边界条件等在骤变的环境因素影响下发生突变，造成信号的速度、能量等特征突变，但突变的概率相对较低，造成个别特征的孤立分布，易被训练为奇异畸变分量，从而降低了GMM的可靠性。损伤监测过程中需要通过GMM拟合所提取的信号特征参数的概率分布，因此所建立的GMM稳定性和准确度直接影响损伤监测效果。针对这些问题，Chakraborty等[16]采用基于狄利克雷过程的高斯混合模型，在载荷大小周期变化的铝板上实现裂纹监测，但是该方法计算量大，模型建立过程复杂。

笔者提出了一种基于导波强化裂变聚合概率模型的损伤监测方法。首先，对时变环境下获取的导波信号特征样本建立GMM，提出的奇异强化评估条件能够识别GMM中的奇异分量；其次，通过裂变聚合操作修正分布不合理的高斯分量，避免GMM出现局部极值及畸变的问题，实现时变环境下的稳定可靠建模；最后，采用概率分量最小匹配KL距离定量计算监测时的动态GMM相对于健康状态下的基准GMM的概率分布差异，据其变化趋势评估结构健康状态。真实大梁验证实验结果表明，本方法能够在时变环境下有效提高导波概率模型的稳定性且避免奇异情况，从而提高损伤监测稳定性及可靠性。

1 高斯混合模型基本原理

假设F={X1, …,Xr, …,XR}为一组随机分布的导波信号特征样本集，由R个导波信号特征样本Xr构成，其中r=1, 2, …,R；Xr= [x1, …,xd, …,xD]T为一个D维的特征样本，其中d= 1, 2, … ,D。笔者假设导波特征样本集F服从高斯混合模型分布，即由强化裂变聚合建模算法建立的概率模型为高斯混合模型，其概率密度函数表达式为

(1)

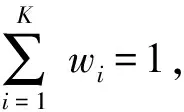
Φi表示为

(2)

其中：μi，Σi分别为第i个高斯分量的均值向量和协方差矩阵。

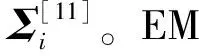
(3)

2 强化裂变聚合模型损伤监测原理

2.1 损伤监测原理

本方法的基本监测原理如下：首先，在结构健康状态下基于导波特征参数采用强化裂变聚合建模算法建立基准GMM；其次，在线监测过程中同样采用强化裂变聚合建模算法建立动态GMM。在时变环境因素的影响下，结构导波特征参数概率分布出现随机性变化。如果结构中出现裂纹等不可逆损伤时，导波特征参数概率分布会产生不同于环境因素影响下的累积迁移，因而可通过动态GMM相对于基准GMM的概率分布迁移趋势评估结构损伤状态。本研究损伤监测方法原理如图1所示。

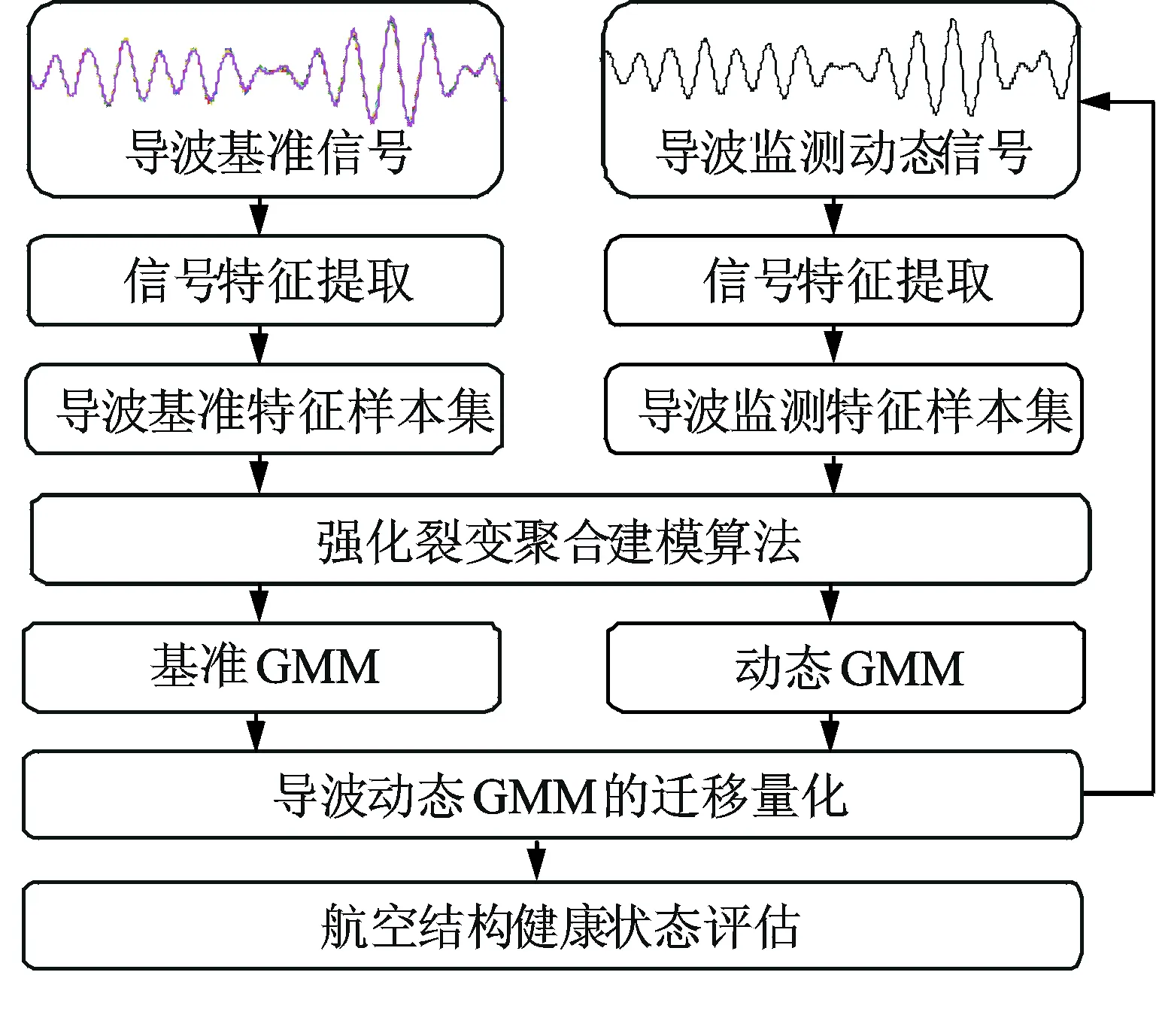
图1 损伤监测方法原理框图Fig.1 The implementation process of the proposed method

2.2 强化裂变聚合建模算法

EM算法建立的GMM易受初始状态影响收敛于局部极值，具体表现为GMM部分高斯分量在样本分布密集区域分布分散，在样本分布分散区域高斯分量分布反而集中，与特征样本实际概率分布不符[13]。针对该现象，笔者在EM算法建立的GMM基础上，对其分布较密集的高斯分量进行聚合，较为分散的高斯分量进行裂变，最终修正GMM。强化裂变聚合建模算法原理如图2所示。

具体步骤如下。

1) EM算法建立初始化GMMΦ。

2) 选择Φ中需要裂变和聚合的高斯分量。如果很多样本属于两个分量的后验概率相似，说明这两个分量覆盖的样本重叠部分较多，故后验概率相似度越高的两个分量应该聚合[15]。样本Xr属于分量Фi的后验概率Pri(Xr|Φ)如式(4)所示，两个分量之间的后验概率相似度如式(5)所示

(4)

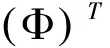
(5)

其中：Pi(Φ)和Pj(Φ)分别为Φ中第i个和第j个高斯分量对应的R维后验概率向量，如Pi(Φ)={P1i(X1|Φ), …,Pri(Xr|Φ), …,PRi(XR|Φ)}T。

首先，将相似度J值进行排序，前C个较大J值对应的两个高斯分量作为待聚合的分量，C≤0.5K(K-1)；其次，可在Φ中剩下的K-2个分量中任意挑选一个高斯分量进行裂变。这样一共选出M个待裂变聚合的高斯分量组合，M=C(K-2)。

3) 线性裂变聚合操作。假设Φ中第i个和第j个分量聚合成一个分量Φi’，聚合时两分量的均值按权值比例进行线性叠加，如式(6)所示；第k个分量裂变成分量Φj’和Φk’，均值裂变如式(7)所示

(6)

(7)

其中：ε'和ε''为两个不同的极小量，且满足式(8)。

(8)

4) 模型重建。线性裂变聚合后，需要将Φi’，Φj’与Φk’连同Φ中未裂变聚合高斯分量的均值一起作为K均值算法的初始值，并通过K均值算法重新对样本集进行聚类，聚类结果作为EM算法的初始值经EM算法重新训练GMM。

对于步骤1选出的M组裂变聚合分量，重复上述步骤3和步骤4，得到M个重建GMMΦ′。

5) 强化评估。为避免重建后的GMM因高斯分量畸变而出现奇异情况，笔者提出两级奇异强化评估条件排除重建后的畸变GMM。在所有通过强化条件的重建GMMΦ′中，选出对数似然函数值最大的Φ′，如果Φ′的对数似然函数值L′大于Φ的L，则将Φ′代替Φ，并重复上述步骤2～步骤5；若所有Φ′均未通过强化条件，或通过强化条件的Φ′对应的L′没有增加，则算法结束，Φ为最终强化裂变聚合建模算法训练的GMM。

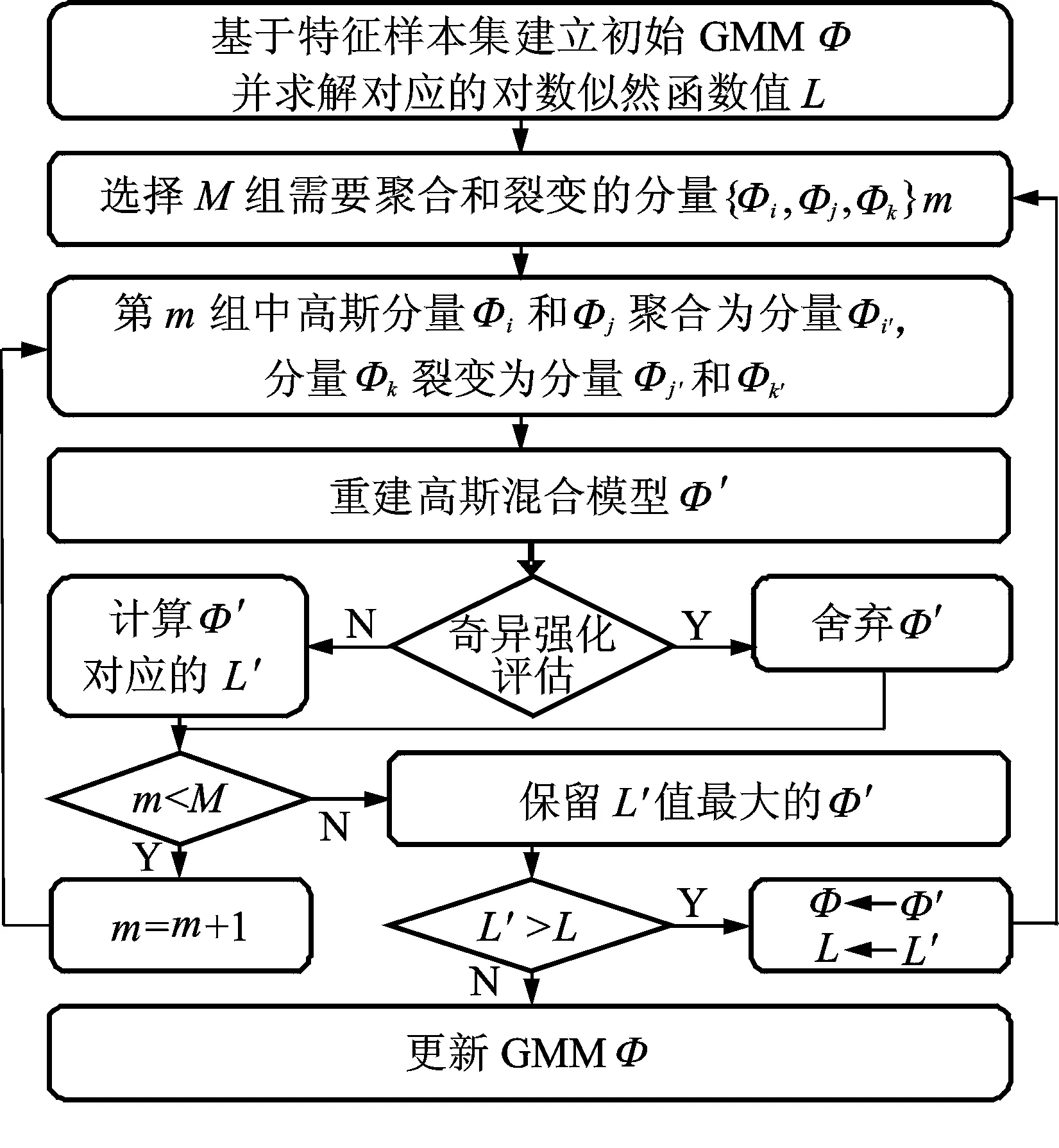
图2 强化裂变聚合建模算法原理框图Fig.2 The implementation process of the enhanced split-merge probability model algorithm

2.3 奇异强化评估条件

在EM算法收敛过程中，当属于一个高斯分量的样本数目不大于样本维度时，即分量Φi对应的后验概率向量Pi(Φ)中不为0的元素数目小于样本维度D时，Σi奇异。故本研究的第1级强化条件为：隶属于GMM中每个分量的特征样本个数是否都大于样本维数D，具体表示为

(9)

当GMM中某些分量畸形，例如二维样本空间中，GMM中一个分量Φi在一个维度上几乎没有分布，该维度上的样本集方差接近于0，故协方差矩阵Σi行列式接近于0，此时Σi也奇异。故第2级强化条件为当GMM中存在一个分量，其协方差矩阵的最小和最大特征值之比越小，说明该分量在两个维度上分布差异太大，如果该比值小于设定的阈值ε，则判定该GMM存在畸形分量，具体条件为

(10)

其中：λi,d为第i个高斯分量的协方差矩阵的第d个特征值，本研究阈值ε取为10-5～10-3。

2.4 概率模型迁移指标

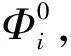
(11)

(12)

当动态GMM与基准GMM的差异越大时，概率迁移指标MI值也会变大，故可通过MI值的迁移变化趋势对结构中的损伤状态进行评估。

作为援藏干部，一般一轮是3年。但每一轮援藏快结束时，他都有无可辩驳的理由继续——第一次是要盘点青藏高原的植物家底；第二次是要把西藏当地的人才培养起来；第三次是要把学科带到一个新的高度。

3 实验验证

3.1 实验设备及过程

在真实飞机大梁结构上对方法进行了验证实验，如图3所示。

实验装置如图3(a)所示。由于连接大梁与飞机蒙皮的螺钉部位易因应力集中产生孔边裂纹，故验证中在3号螺钉孔边贴上吸收导波能量的正方形胶体以模拟裂纹损伤，并控制其边长量化损伤大小。飞机服役过程中，螺钉松紧会随其受力大小变化，使得监测区域内的边界条件不断变化，故实验中改变螺钉的松紧状态以模拟环境因素变化。

监测区域内传感器、螺钉位置及模拟损伤具体位置如图3(b)所示,其中压电传感器1为导波激励元件，压电传感器2为响应元件。导波激励信号为正弦调制五波峰信号，中心频率及幅值分别为200kHz及±70V，采样率为10MSamples/s。

图3 飞机大梁模拟裂纹监测实验(单位：mm)Fig.3 Crack monitoring experiment of the aircraft wing spar(unit :mm)

整个验证主要分为两大部分。

1) 基准信号的获取：a.在螺钉拧紧状态下采集1次导波信号，然后依次松动2，4，6号螺钉再拧紧，各采集1次信号；b.重复上述步骤10次。采集40次基准导波信号，编号为m1(t)～m40(t)。

2) 在线监测过程中动态信号的获取：a.重复10次基准信号获取中的步骤a，采集40次基准信号；b.粘贴边长为4mm的正方形吸波胶体，重复20次步骤a；c.增加胶体边长至8mm，重复20次步骤a；d.增加胶体边长至12mm，重复20次步骤a；e.增加胶体边长至16mm，重复20次步骤a。在线监测过程中共获取了360个监测动态信号，依次编号为m41(t)～m400(t)。

3.2 信号特征提取及时变因素影响分析

损伤监测过程中需不断观测导波信号是否发生异变来评判结构中的损伤状态，这就需要提取能够反映导波信号变化的损伤因子(damage index，简称DI)。本研究提取的两种损伤因子如下。

1) 衡量动态信号与基准信号间相关程度的互相关损伤因子

(13)

2) 只与信号幅度相关的频谱幅度差损伤因子

(14)

整个监测过程中的导波信号损伤因子计算结果如图4所示。在结构健康状态下，只有螺钉松紧这一边界条件发生变化时，损伤因子也会发生变化。对比有无裂纹时损伤因子大小，发现并不能单从其数值变化上评判裂纹情况，所以并不能通过常规的设定阈值方法来评估损伤状态。

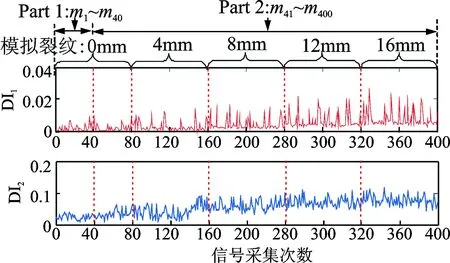
图4 损伤因子结果Fig. 4 Damage indexes results

3.3 高斯混合模型及其动态迁移

实验中将每个信号对应的DI1,r和DI2,r组成损伤特征样本Xr=[DI1,r,DI2,r]，基准信号m1(t)～m40(t)对应的样本构成基准特征样本集F0={X1,X2, … ,X40}。基准GMMΦ0如图5(a)所示。本研究GMM所含分量个数K为5，利用等高线图表征GMM的分布情况，一个等高椭圆圈代表一个高斯分量。

对于同样的基准样本集F0，运行EM算法20次，出现图5中的5种局部极值GMM结果，每个GMM对应的对数似然函数值L如表1所示。由表1可知，EM算法结果都没有本研究算法对应的L值大，这说明EM算法不稳定，训练的GMM易收敛于局部极值，训练结果不唯一。以图5中5个局部极值GMM作为本算法的初始值，最终建立的GMM都如图5(a)所示，结果唯一。可见本研究算法有效解决了EM算法局部极值问题，能够建立稳定的GMM。

图5(d)，(e)，(f)所示的GMM都存在奇异分量(红色圆圈圈出的分量)，这些分量只包含一、二个样本，符合第1个奇异强化条件，而提出的算法通过将其与其他分量合并的方式修正这些分量。图5(a)中的GMM将图5(d)，(e)，(f)中的奇异分量与其邻近高斯分量合并，消除了此类奇异分量。

从以上分析来看，提出的强化裂变聚合建模算法不仅解决了常规EM算法局部极值问题，且不会出现奇异分量，建立的GMM稳定且可靠。

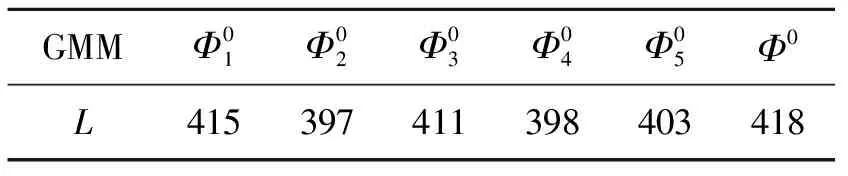
表1 所有基准GMM对应的似然函数值

在线监测时需不断更新监测样本集，更新方式为先进先出。如监测次数n为1时，将新获取的动态特征样本X41添加到F0的最后，而F0中第1个样本X1被舍弃，故监测样本集F1={X2,X3, …,X41}。随后建立动态GMM，监测时典型动态GMM如图6所示。

图6(b)是在结构没有裂纹的情况下建立的。在边界条件变化的影响下，部分特征样本发生随机性偏移，但图6(b)中的GMM概率分布与图6(a)中基准GMM基本一致，不会因信号特征的随机变化而改变GMM分布形式。在裂纹产生并扩展后，GMM中的高斯分量分布形式发生累积性的旋转、扩张、缩小及迁移等变化。在结构中裂纹的影响下，动态监测特征样本集的概率分布相较于基准特征样本集的概率分布发生累积性迁移变化。

3.4 损伤监测结果及分析

监测过程中概率模型迁移指标MI计算结果如图7所示。首先，在前40次损伤监测过程中，GMM迁移指标MI值基本为0，说明此时没有模拟损伤，虽然此阶段大梁边界条件一直在变化，但环境因素对研究的概率迁移指标没有影响；其次，从第40次开始，MI数值不再为0，动态GMM与基准GMM开始有了差异，说明此时结构中已经产生了损伤；此后的MI数值呈现明显的阶梯性，MI数值越大，表明结构上的模拟裂纹长度越大。整个监测过程中，虽然大梁的边界条件一直在变化，但是MI的数值变化准确可靠地反应了结构上模拟裂纹的变化，故笔者提出的基于导波强化裂变聚合概率模型可在时变环境中进行可靠且稳定的损伤监测。

图5 基准GMM及陷入局部极值的基准GMM对比分布图Fig.5 Comparison between baseline GMM and local extremum GMMs

图6 模拟裂纹长度各阶段典型GMM变化示意图Fig. 6 Variation demonstration of the typical GMMs in different stages of simulated crack length

将图7给出的监测结果与图4给出的基于导波损伤因子的监测结果相比，在时变边界条件影响下，损伤扩展的监测可靠性得到明显提高。基于图7的结果，还可以很容易地设定损伤判别阈值，实现损伤报警。

为验证导波强化裂变聚合概率模型损伤监测方法的稳定性，共运行本研究方法和由EM算法建立的常规GMM损伤监测方法各10次，分别计算概率模型迁移指标MI值，结果如图8所示。笔者提出的方法结果只有1种，如图8中红线所示，也与图7中结果一致；但是常规GMM损伤监测结果却出现了图8中的其他3种结果。常规GMM损伤监测方法出现多种结果的原因为一般EM算法训练的GMM不稳定，但笔者提出的建模算法运行多次，每一次建立的概率模型稳定且唯一，故最终的损伤监测结果更为稳定可靠。从图8的MI值比较结果来看，所提方法有效提高了损伤监测的稳定性和可靠性。

图7 所提方法的实验损伤监测结果Fig. 7 Experimental damage evaluation result of the proposed method

图8 所提方法和常规GMM损伤监测方法的损伤监测结果对比图Fig. 8 Comparison of the damage monitoring results based on the proposed method and ordinary GMM damage monitoring method

4 结 论

1) 笔者提出的导波强化裂变聚合概率模型损伤监测方法，在结构处于健康状态下，基于获取的导波特征参数采用强化裂变聚合建模算法建立基准GMM，在监测过程中同样采用强化裂变聚合建模算法建立动态GMM，通过对比动态监测GMM的累积迁移趋势，实现时变环境下的可靠损伤监测。

2) 提出的含裂变聚合操作的GMM建立算法，避免了常规EM算法收敛于局部极值的问题，同时提出的两级奇异强化评估条件，准确描述了奇异高斯分量的两个特征，并通过聚合操作修正畸变分量，进而提高了时变环境下采用GMM方法进行航空结构损伤监测的稳定性。

3) 在真实飞机大梁结构上进行了边界条件变化下的模拟裂纹监测验证实验。验证结果表明，本研究方法能够在时变边界条件影响下实现损伤的可靠和稳定监测，且与基于损伤因子及常规GMM的导波监测方法相比，其损伤监测的可靠性及稳定性得到明显提高。

参 考 文 献

[1] Esperon-Miguez M, John P, Jennions I K. A review of integrated vehicle health management tools for legacy platforms: challenges and opportunities[J]. Progress in Aerospace Sciences, 2013, 56: 19-34.

[2] 袁慎芳. 结构健康监控[M]. 北京: 国防工业出版社, 2007: 1-22.

[3] 孙侠生, 肖迎春. 飞机结构健康监测技术的机遇与挑战[J]. 航空学报, 2014, 35(12): 3199-3212.

Sun Xiasheng, Xiao Yingchun. Opportunity and challenges of aircraft structural health monitoring[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(12): 3199-3212. (in Chinese)

[4] 屈文忠, 李拯, 王芝, 等. 基于非线性超声调制方法的损伤识别与定位[J]. 振动、测试与诊断, 2016, 36(5): 852-857.

Qu Wenzhong, Li Zheng, Wang Zhi, et al. Damage detection and localization using nonlinear ultrasonic modulation method[J]. Journal of Vibration, Measurement & Diagnosis, 2016, 36(5): 852-857. (in Chinese)

[5] 刘彬, 邱雷, 袁慎芳, 等. 复合材料T型接头损伤监测的概率成像方法[J]. 振动、 测试与诊断, 2015, 35(3): 519-524.

Liu Bin, Qiu Lei, Yuan Shenfang, et al. The probability imaging algorithm of composite T-joint damage monitoring[J]. Journal of Vibration, Measurement & Diagnosis, 2015, 35(3): 519-524. (in Chinese)

[6] 孙汝杰, 陈国平, 孙东阳, 等. 核密度估计法在板件概率损伤识别中的应用[J]. 振动、 测试与诊断, 2015, 35(6): 1055-1062.

Sun Rujie, Chen Guoping, Sun Dongyang, et al. Probabilistic damage detection based on the kernel density estimation method in aluminum plates[J]. Journal of Vibration, Measurement & Diagnosis, 2015, 35(6): 1055-1062. (in Chinese)

[7] 张伟伟, 武静, 马宏伟. 基于Lyapunov 指数的超声导波检测技术[J]. 振动、 测试与诊断, 2015, 35(2): 250-257.

Zhang Weiwei, Wu Jing, Ma Hongwei. Ultrasonic guided wave inspection method based on Lyapunov exponents[J]. Journal of Vibration, Measurement & Diagnosis, 2015, 35(2): 250-257. (in Chinese)

[8] Schubert K J, Brauner C, Hermann A S. Non-damage related influences on lamb wave based SHM of CFRP structures[J] .Structural Health Monitoring, 2014, 13(2): 158-176.

[9] Wang Yishou, Gao Limin, Yuan Shenfang, et al. An adaptive filter-based temperature compensation technique for structural health monitoring[J]. Journal of Intelligent Material Systems and Structures, 2014, 25(17): 2187-2198.

[10] Lim H J, Sohn H, DeSimio M P, et al. Reference-free fatigue crack detection using nonlinear ultrasonic modulation under various temperature and loading conditions[J]. Mechanical Systems and Signal Processing, 2014, 45(2): 468-478.

[11] Banfield J , Raftery A. Model-based Gaussian and non Gaussian clustering[J]. Biometrics, 1993, 49(3): 803-821.

[12] Banerjee S, Qing X L P, Beard S, et al. Prediction of progressive damage state at the hot spots using statistical estimation[J]. Journal of Intelligent Material Systems and Structures, 2010, 21(6): 595-605.

[13] Kullaa J. Structural health monitoring under nonlinear environmental or operational influences[EB/OL]. Shock and Vibration, [2014-05-29]. http:∥dx.doi.org/10.1155/2014/863494.

[14] Qiu Lei, Yuan Shenfang, Chang F K, et al. On-line updating Gaussian mixture model for aircraft wing spar damage evaluation under time-varying boundary condition[J]. Smart Materials and Structures, 2014, 23(12): 125001.

[15] Ueda N, Nakano R, Ghahramani Z, et al. SMEM algorithm for mixture models[J]. Neural Computation, 2000, 12(9): 2109-2128.

[16] Chakraborty D, Kovvali N, Papandreou-Suppappola A, et al. An adaptive learning damage estimation method for structural health monitoring[J]. Journal of Intelligent Material Systems and Structures, 2015, 26(2): 125-143.

[17] Goldberger J, Gordon S, Greenspan H. An efficient image similarity measure based on approximations of KL-divergence between two Gaussian mixtures[C]∥Ninth IEEE International Conference on, Proceedings Ninth IEEE International Conference on Computer Vision. France: IEEE, 2003: 487-493.