改进的浸入边界-晶格Boltzmann法的蠕动流分析*

任晓飞， 魏守水， 刘飞飞， 张 玲， 王少伟， 许明田

(1.山东大学控制科学与工程学院 济南，250061) (2.山东大学数学学院 济南，250061) (3.山东大学土建与水利学院 济南，250061)

引 言

蠕动流是由管壁的蠕动引起的管道内部液体的流动。其驱动原理与效果一直是生理学及工程领域研究的热点。如食糜在肠道中的运动[1]、输卵管中卵子的运输[2]、子宫内液体的运动[3]及胚胎心脏的泵血[4]均属蠕动流。文献[5-6]对蠕动流的速度、压力分布以及蠕动流特有的“回流”和“陷圈”现象做了研究。Hanin[7]研究了以蠕动效应为机理的流体输运性质。Weinberg等[8]通过实验证实了现有理论下蠕动流的基本流动特征。Haroun[9]研究了在非对称管道中管壁顺应性对牛顿液体的蠕动传输的影响。Srinivas等[10]研究了二维非对称斜管道中黏性不可压缩液体的磁流体重力流问题。这些研究都是在低雷诺数、长波和(或)小振幅的假设条件下进行的，这为理论分析带来方便，但与真实的流动问题颇有差距。另外，所用方法为传统的数值方法，如有限元法[11]和有限差分法[12-13]，这些方法在处理边界的非线性运动与流体流动之间的相互作用时有诸多限制，如网格重建困难、耗时长及计算成本大等。

浸入边界法[14](immersed boundary method, 简称IBM)是将浸入流体的边界变形产生的力分布到周围流体，用体积力描述浸入边界的运动，再根据周围流体的速度更新浸入边界的位置和速度，以此来描述流体-边界之间的相互作用。因此，选择合适的数值方法通过固定、规则的欧拉网格计算流场可以避免动边界问题。对于复杂的浸入边界结构，如红细胞的变形[15]、血小板的聚集[16]、精子的游动[17]、纤毛的波动[18]及昆虫的飞行[19]等，均取得了较好的效果。晶格玻尔兹曼方法(lattice Boltzmann method, 简称LBM)[20]采用固定的欧拉网格代表流场，将连续流体假想为分布到欧拉网格上的离散粒子，克服了传统计算流体力学方法中网格重新生成和自适应网格变换的困难，降低了计算成本。此外，由于它的并行性和扩展性，边界条件容易处理，被广泛用于研究多相流、非牛顿流体、悬浮粒子流、微流体和多孔流[21-25]等复杂流体的流动。文献[26-28]分别用IBM和LBM研究了宏观颗粒通过蠕动泵在牛顿流体中的输运。Waldrop 等[29]用IBM研究了短波和大振幅的流体蠕动。

笔者基于一种改进的浸入边界-晶格玻尔兹曼方法(modified immersed boundary-lattice Boltzmann method,简称MIB-LBM)研究蠕动流。将变形管壁的运动速度作为速度源引入晶格玻尔兹曼方程(lattice Boltzmann equation, 简称LBE)中，避免了传统IB-LBM中边界变形产生的力的复杂计算，简化了计算过程。这种方法已经成功应用于研究弹性细丝的周期性波动对流体的驱动作用[30]。与传统的IB-LMB及其他的数值方法相比，MIB-LBM计算过程简单，计算效率高，流体和固体之间的相互作用容易实现，而且打破了传统数值方法在研究蠕动流时对波幅和波长大小的限制。

1 理论方法与数值模型

1.1 晶格玻尔兹曼方法

LBM将流体抽象为大量具有离散速度的微观流体粒子的集合，流体粒子在离散晶格上按一定规则进行迁移和碰撞，通过粒子密度分布函数与宏观流动变量之间的关系获得宏观流动信息。其理论模型中D2G9是一种不含压缩效应的LBGK模型，它通过Chapman-Enskog展开可以导出标准的不可压Navier-Stokes方程组，适合不可压缩流分析。笔者选用D2G9模型[31]。

1.2 浸入边界法的改进

图1为浸入边界法示意图，其中空心点和实心点分别表示流体结点和浸入边界结点。传统的IBM将浸入边界变形产生的力通过Dirac delta函数分布到周围流体网格点上，然后流体再通过速度u影响浸入边界的变形，控制方程[32]为

(1)

(2)

其中：x=(x,y)为流体网格点的位置；l为浸入边界的长度；X=(X,Y)为浸入边界上的点；F(X,t)为边界变形产生的力密度；fb(x,t)为边界传递给流场的体积力；u(x,t)=(ux,uy)为流体速度；U(X,t)=∂X/∂t为浸入边界的运动速度；δh(x-X)为Dirac delta函数。

给出其定义

(3)

其中：h=Δx为格子单位。

图1 浸入边界法示意图Fig.1 Schematic diagram of the immersed boundary method

由于蠕动流问题中行波的位置及运动信息都包含在其速度信息内，笔者采用的MIB-LBM直接将弹性管壁的运动速度通过Dirac delta函数引入LBE，形成如下控制方程

(4)

u(x,t+Δt)=u(x,t)+Δu(x,t)

(5)

边界速度U(X,t)通过Dirac delta函数分布到周围流体网格结点上，式(4)和式(5)描述了管壁运动与流体流动之间的耦合关系。该方法避免了边界变形产生的力的复杂计算，简化了计算程序。

1.3 数值模型

基于MIB-LBM分析了二维管道中蠕动流的驱动原理，其二维模型如图2所示。将管壁看作浸入空气和液体之间的边界，管道内充满黏性不可压缩的牛顿流体，初始状态为静态。计算区域的长度和高度分别为L和H，管道进出口采用非平衡外推边界条件[33]，波动管壁采用无滑移反弹边界条件[34-35]，将计算区域均匀离散化为Nx×Ny的固定欧拉网格，将做行波运动的管壁均匀离散化为一系列可动的拉格朗日节点，其水平坐标为X′，竖直坐标为Y′，行波速度为c′。其控制函数为

(6)

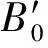
图2 二维模型图Fig.2 The two-dimensional model diagram

为了方便计算，将式(6)中的参数转化为无量纲形式，转化规则如下

(7)

其中：ν为流体运动黏度；φ为振幅比；α为归一化的波数；Re为雷诺数。

2 结果和讨论

为了计算收敛，在波开始形成时引用以下约束方程

(8)

其中：t0为常数，表示波开始形成的时间。

进出口处流体的瞬时流量Q(t)为

(9)

其中：ux(l,y,t)为t时刻(l,y)处的流体速度在x方向的分量，当流量为正时表示液体正向(向右)流动，当流量为负时表示液体反向(向左)流动。

时间t内管道出口处累积流出的液体体积Vout为

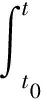
(10)

管道出口处的时间平均流量Qavg为

(11)

流量对应的无量纲形式为

(12)

当管道两端施加的压力差为0时, Jaffrin等[6]在低雷诺数和长波近似的条件下得到无量纲流量与振幅比的关系

(13)

为了验证该方法的正确性，在长波近似和低雷诺数的条件下，获得平均流量Θavg与振幅比φ的关系，并与文献[6]得到的结果相比较，如图3所示。从图中可以看出，即使在振幅比较大时，本研究仿真结果与理论值仍吻合良好。

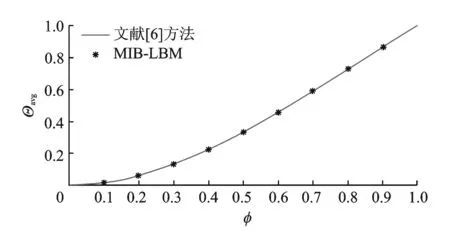
图3 平均流量Θ与振幅比φ的关系Fig.3 Relationship between the time-mean flow and the amplitude ratio

2.1 流场与流量分析

笔者分析了蠕动流在一段时间内的运动结果。图4分别为不同时刻管道内的速度分布以及流线图，图中箭头表示速度方向，颜色表示速度幅值。从图中可以观察到，随着管壁行波沿着x方向传播，管壁收缩部分的流体沿着与波相反的方向流动，管壁扩张部分的流体沿着与波相同的方向流动，这与文献[6]描述相同。同时可以看出，管壁变形幅度大的区域(红色区域)的流体速度大于管壁变形幅度小的区域(蓝色区域)的流体速度。

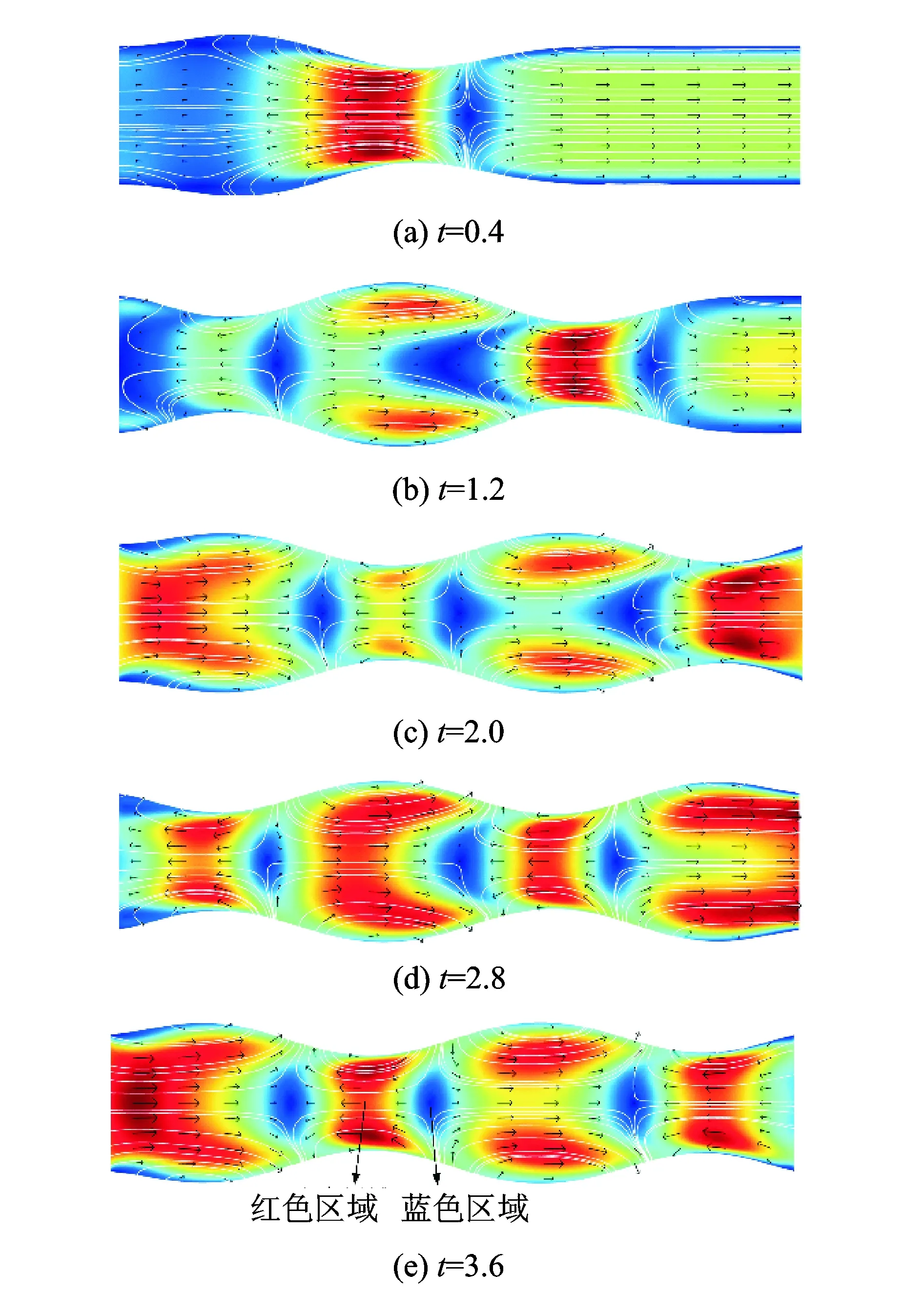
图4 t=0.4, 1.2, 2.0, 2.8, 3.6的速度分布以及流线图Fig.4 Snapshots of the velocity distribution and streamlines at t=0.4, 1.2, 2.8, 3.6

图5(a)描绘了管道出口处瞬时流量Θout随时间t的变化过程。Θout初始为0，在t0=0.1时波开始形成，波幅从0开始增大，使管道内压强增大，挤压管道内的液体流动，Θout增大；在波向右传播的过程中，波的扩张部分开始出现，使管道内压强减小，Θout减小，流体运动速度减小，甚至向着相反方向运动。通过分析可以发现，在t=3.1以后，Θout趋于周期性稳定。

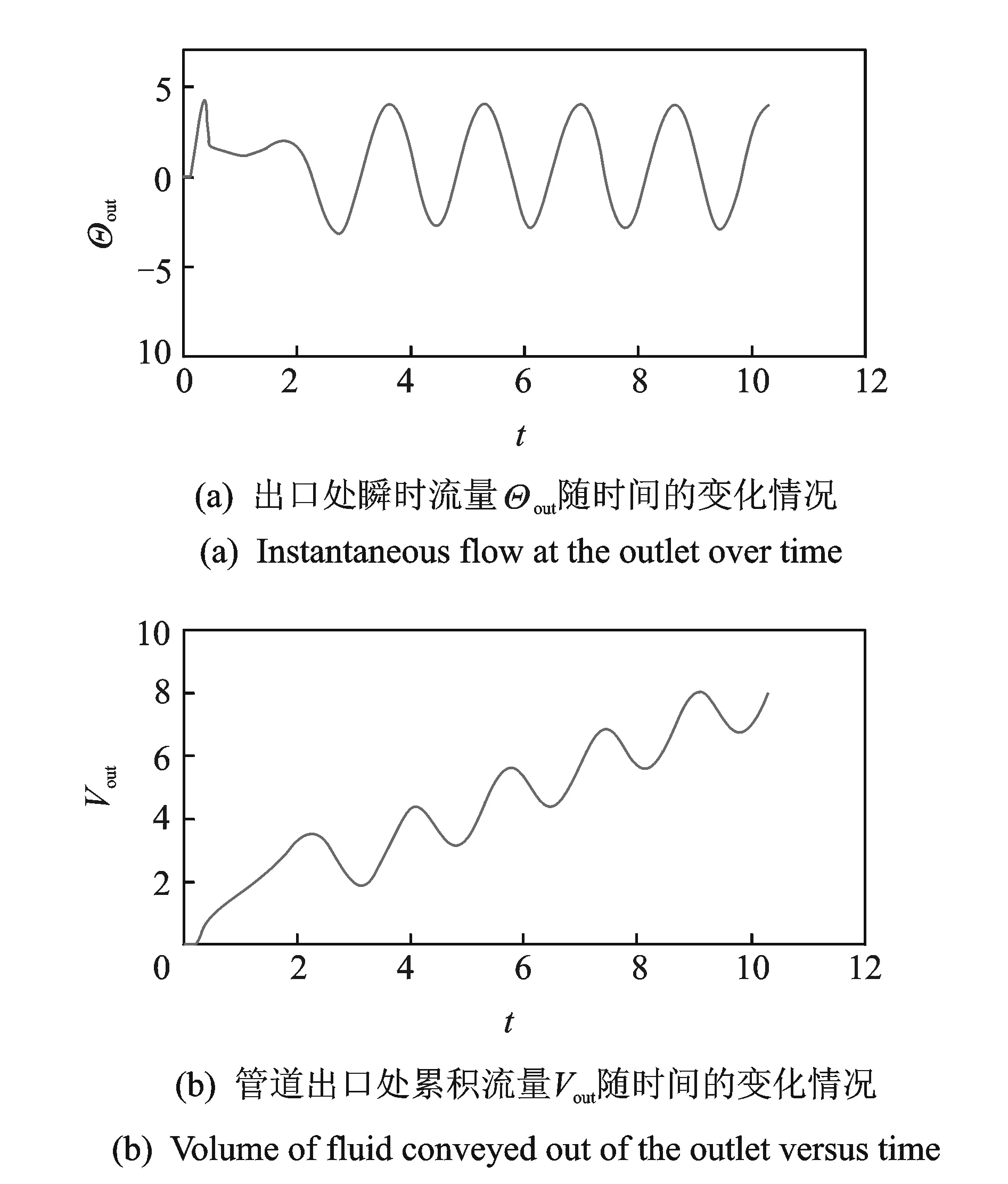
图5 流量随时间的变化情况Fig.5 Flow over time

图5(b)描绘了时间t内管道出口处累积流出的液体体积Vout。通过分析知道，曲线上升区间对应Θout>0的部分，曲线下降区间对应Θout<0的部分，而且随着时间的增加，Vout总体呈增大趋势。尽管管道内液体的流动随着管壁行波的传播改变方向，但由曲线可以看出，Vout总是大于零，说明管壁蠕动对管道内的流体具有正向驱动作用。

2.2 参数分析

对于周期性的行波而言，蠕动流问题主要由振幅比、频率、雷诺数(液体黏度)和波数决定。

2.2.1 振幅比φ对流量的影响

通过改变波幅B0来调节振幅比φ，图6所示为振幅比对流量的影响。从图6(a)可以看出，随着φ的增大，Θout的幅值增大。图6(b)为振幅比φ与平均流量Θavg的关系图，从曲线可以看出，Θavg与φ呈非线性增长的关系。这是由于管壁蠕动效应是驱动流体流动的主要原因，随着波形振幅的增大，蠕动效应增强，导致流量增大。

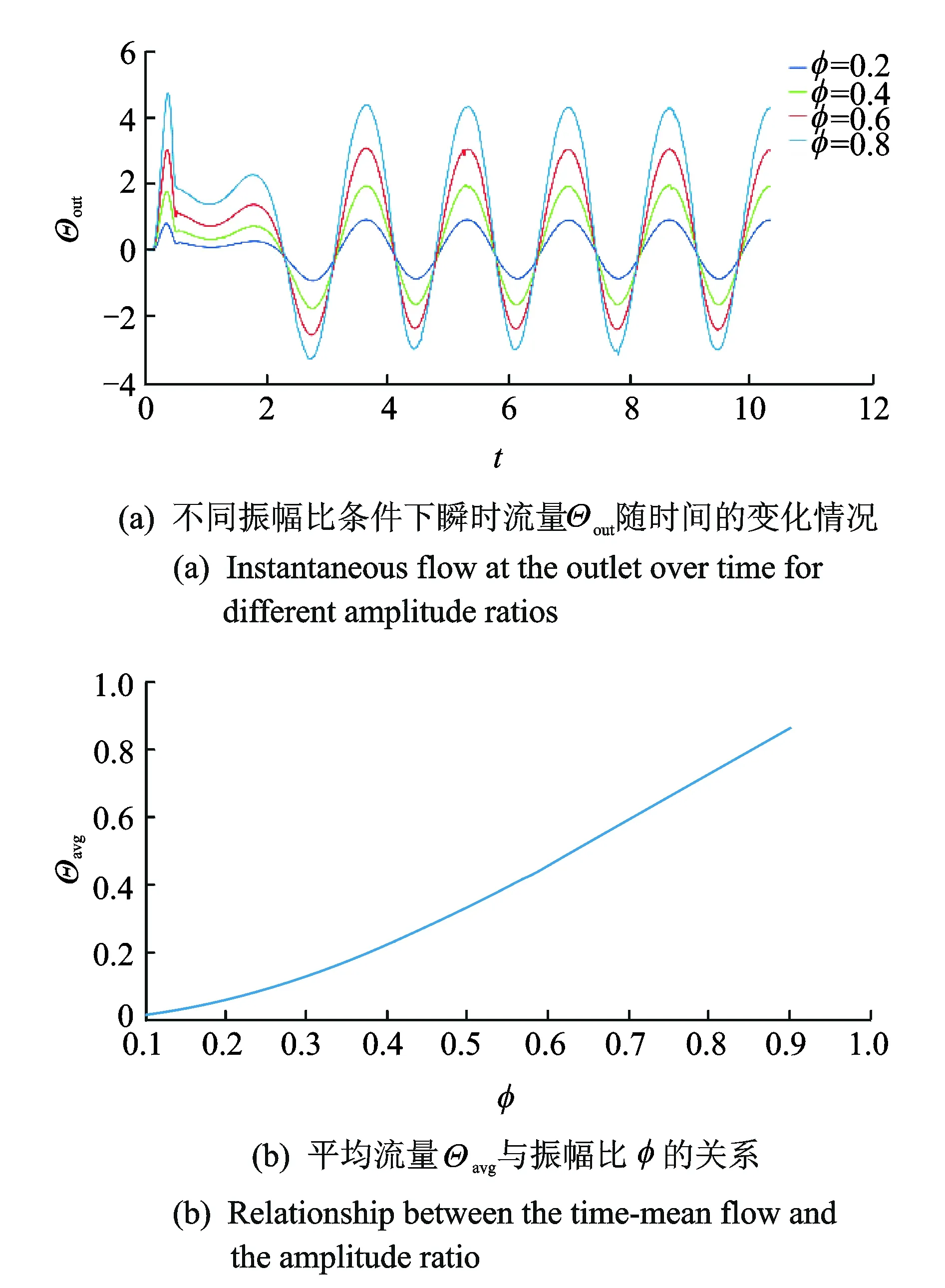
图6 振幅比φ对流量的影响Fig.6 The effect of the amplitude ratio on the flow

2.2.2 频率f对流量的影响

图7描绘了波的频率对流量的影响。当频率增大时，管壁传递给液体的能量增强，导致流量变大。从图7(a)可以看出，Θout幅值随着f频率的增大而增大。图7(b)为频率f与平均流量Θavg的关系图，从曲线可以看出，Θavg随着f频率的增大而线性增大。

2.2.3 液体运动黏度对流量的影响

图8描绘了液体运动黏度ν对流量的影响。从图中8(a)可以看出，总体上ν的改变对Θout的影响较小。图8(b)为ν与平均流量Θavg的关系图，从图中可以看出，当ν<10×10-6m2/s时，Θavg随着ν的增大而迅速减小；当ν>10×10-6m2/s时，Θavg随着ν的增大而缓慢增大；当ν>50×10-6m2/s时，Θavg几乎不再增长。这说明液体黏度相对较小时对流量有一定的影响，当大于一定值时，黏度对流量的影响可以忽略。这是由于当液体黏度较小时,管壁与液体间的作用力占主导作用；随着黏度的变化，管壁与液体之间的作用力变化较快，导致流量迅速变化；当液体黏度增长到一定程度时,液体的黏性阻力占主导作用，随着黏度的增加，流量几乎不再发生变化。

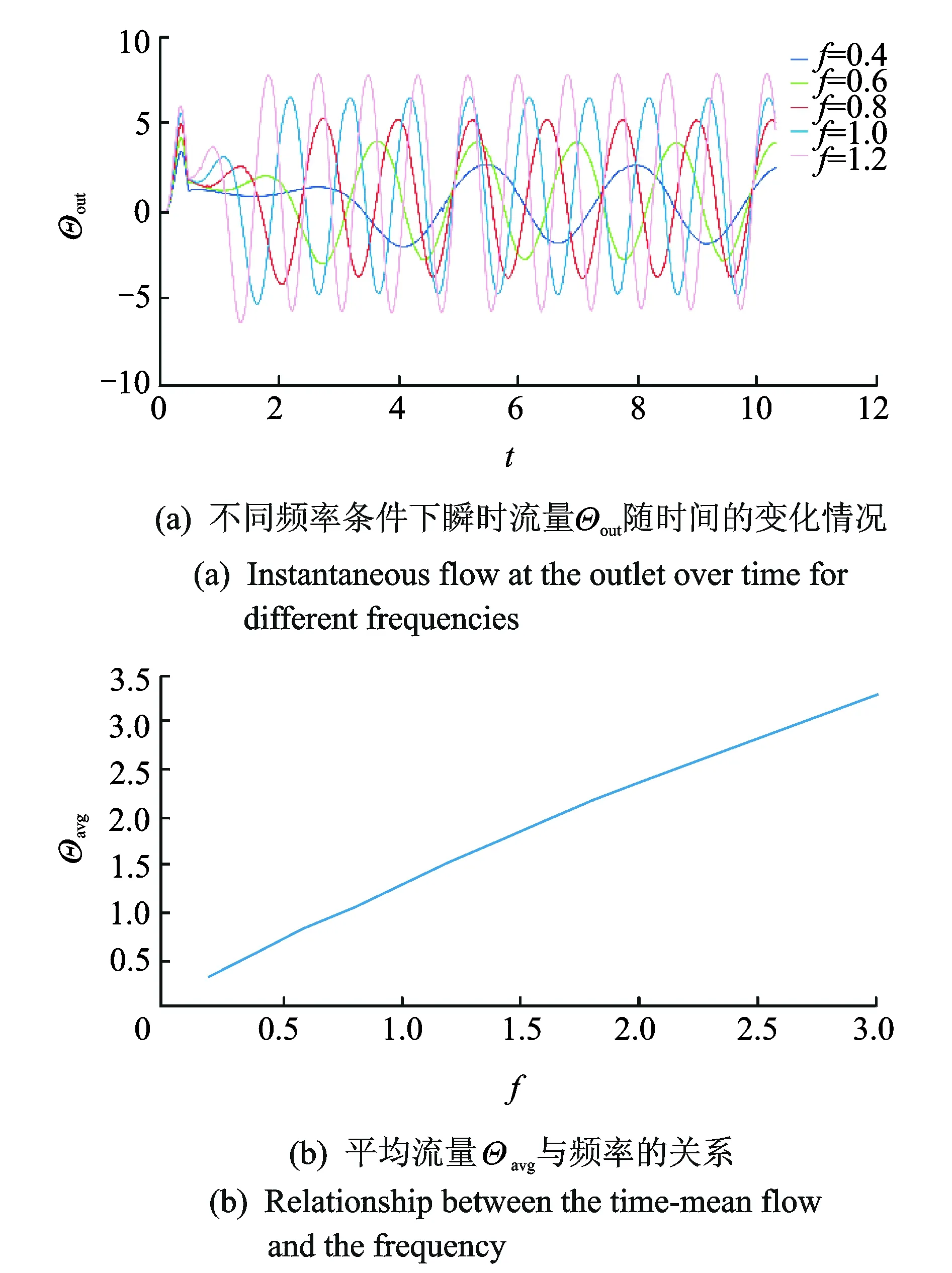
图7 频率f对流量的影响Fig.7 The effect of the frequency on the flow

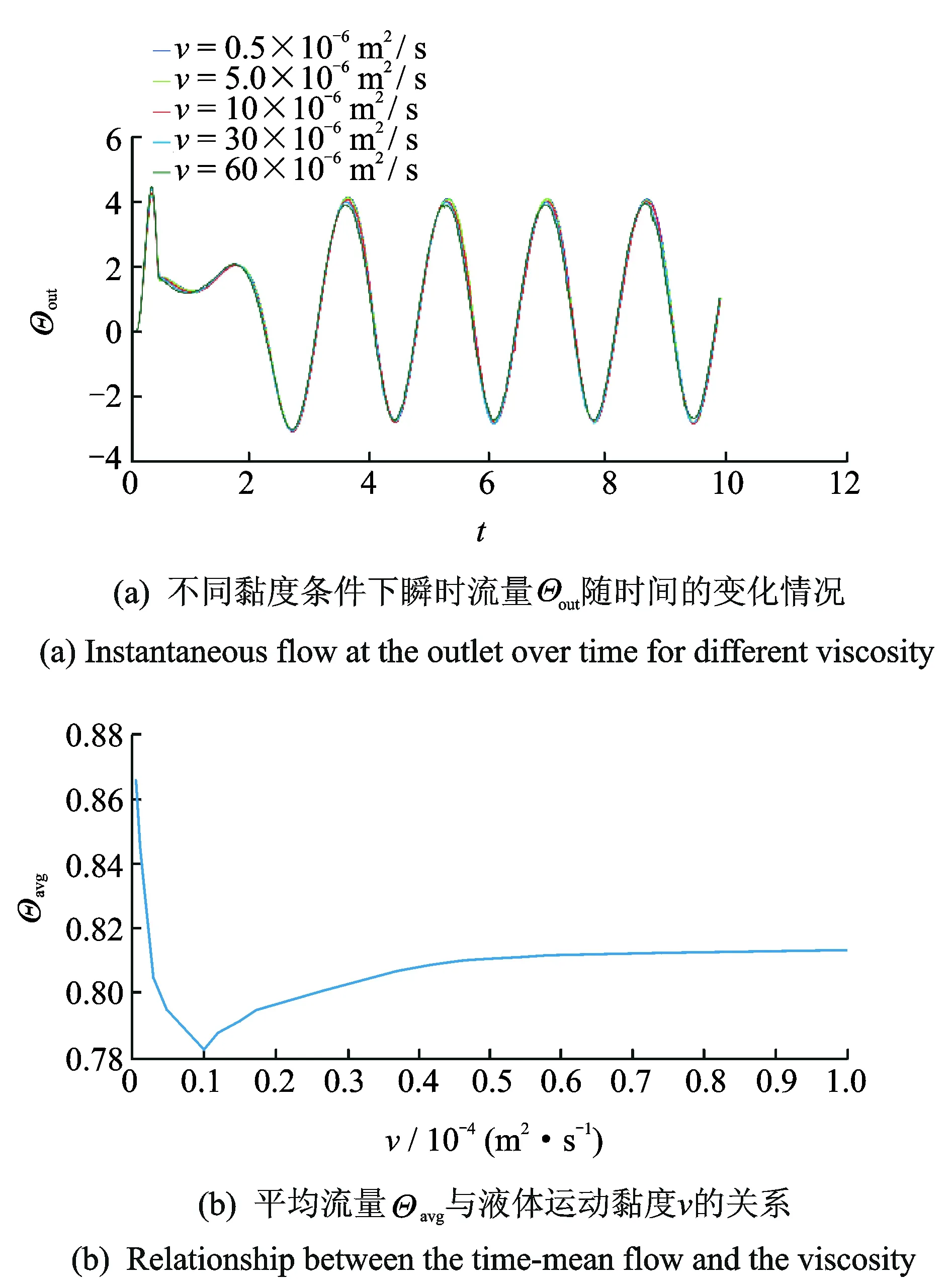
图8 液体运动黏度对流量的影响Fig.8 The effect of the kinematic viscosity of the fluid on the flow

2.2.4 波数α对流量的影响

图9描绘了波数对流量的影响。从图9(a)可以看出，当波速不变时，波数越大，波的频率越大，Θout幅值随着α的增大而减小。图9(b)为波数α与平均流量Θavg的关系图，从曲线可以看出，α与Θavg呈非线性减小关系，并且随着α的增大，Θavg减小趋势变缓。

图9 波数α对流量的影响Fig.9 The effect of the wavenumber on the flow

3 结束语

笔者采用MIB-LBM研究了蠕动流的运动情况，将做行波运动的变形管壁看作浸入空气与液体之间的边界，通过Dirac delta函数直接将变形管壁的运动速度分布到周围流体的网格点上，再用LBM描述流体的运动，克服了传统数值方法在处理动边界时网格重建困难、自适应网格耗时长及计算成本大等诸多困难。为了验证该方法的正确性，在长波近似和低雷诺数的条件下，获得平均流量Θavg与振幅比φ的关系，结果与理论值吻合良好。分析了管壁蠕动过程中管道内的流场分布，获得了出口处流量Θout随时间的变化情况，通过Θout对时间积分获得一段时间内出口处累积流出的液体体积Vout。通过对流场的计算分析了行波驱动原理，从Vout曲线可以看出，出口处流出的液体体积总是大于零，说明管壁上的行波运动对管道内的液体具有正向驱动作用。在此基础上分析了各相关参数对驱动效果的影响，分析发现，振幅比φ、频率f和波数α对出口处的时间平均流量Θavg的影响较大。Θavg随着φ的增大而非线性增大，随着f的增大而线性增大，Θavg与α呈非线性减小关系，并且随着α的增大，Θavg减小趋势变缓。管道中液体运动黏度ν总体上对Θavg的影响较小，分析发现当黏度相对较小时对流量有一定的影响；当黏度大于一定值时，其对于流量的影响可以忽略。仿真结果在较大的振幅比和波数条件下获得收敛的解，并且与已有结果吻合良好，打破了传统方法研究蠕动流时对波幅和波长大小的约束。

参 考 文 献

[1] Barton C, Raynor S. Peristaltic flow in tubes[J]. Bulletin of Mathematical Biology, 1968, 30(4): 663-680.

[2] Blake J R, Vann P G, Winet H. A model of ovum transport[J]. Journal of Theoretical Biology, 1983, 102(102): 145-166.

[3] Eytan O, Elad D. Analysis of intra-uterine fluid motion induced by uterine contractions[J]. Bulletin of Mathematical Biology, 1999, 61(2): 221-238.

[4] Taber L A, Zhang J, Perucchio R. Computational model for the transition from peristaltic to pulsatile flow in the embryonic heart tube[J]. Journal of Biomechanical Engineering, 2007, 129(3): 441-449.

[5] Fung Y C, Yih C S. Peristaltic transport[J]. Journal of Applied Mechanics, 1967, 35(4): 669-675.

[6] Jaffrin M Y, Shapiro A H. Peristaltic pumping[J]. Fluid Mechanics, 1971, 3(3): 13-37.

[7] Hanin M. The flow through a channel due to transversally oscillating walls(mean flow rate calculated for flow in two dimensional channel generated by transverse deflection oscillations along walls)[J]. Israel Journal of Technology, 1968, 6: 67-71.

[8] Weinberg S L, Eckstein E C, Shapiro A H. An experimental study of peristaltic pumping[J]. Journal of Fluid Mechanics,1971,49(3): 461-479.

[9] Haroun M H. Effect of wall compliance on peristaltic transport of a Newtonian fluid in an asymmetric channel[J]. Mathematical Problems in Engineering, 2006, 2006(3): 39-62.

[10] Srinivas S, Pushparaj V. Non-linear peristaltic transport in an inclined asymmetric channel[J]. Communications in Nonlinear Science & Numerical Simulation, 2008, 13(9): 1782-1795.

[11] Tong P, Vawter D. An analysis of peristaltic pumping[J]. Journal of Applied Mechanics, 1972, 39(4): 857-862.

[12] Brown T D, Hung T K. Computational and experimental investigations of two-dimensional nonlinear peristaltic flows[J]. Journal of Fluid Mechanics, 1977, 83(2): 249-272.

[13] Takabatake S, Ayukawa K, Okura M. Numerical analysis of two-dimensional peristaltic flows (3rd report, pumping characteristics of peristaltic transport)[J]. Nihon Kikai Gakkai Ronbunshu B Hen/transactions of the Japan Society of Mechanical Engineers Part B, 1985, 51(467): 2365-2372.

[14] Peskin C S. Flow patterns around heart valves: a numerical method[J]. Journal of Computational Physics, 1972, 10(2): 252-271.

[15] Navidbakhsh M, Rezazadeh M. An immersed boundary-lattice Boltzmann model for simulation of malaria-infected red blood cell in micro-channel[J]. Scientia Iranica, 2012,19(5):1329-1336.

[16] Wang N T, Fogelson A L. Computational methods for continuum models of platelet aggregation[J]. Journal of Computational Physics, 1999,151(2):649-675.

[17] Fauci L J, Mcdonald A. Sperm motility in the presence of boundaries[J]. Bulletin of Mathematical Biology, 1995,57(5):679-699.

[18] Vahidkhah K, Abdollahi V. Numerical simulation of a flexible fiber deformation in a viscous flow by the immersed boundary-lattice Boltzmann method[J]. Communications in Nonlinear Science and Numerical Simulation, 2012,17(3):1475-1484.

[19] Miller L A, Peskin C S. When vortices stick: an aerodynamic transition in tiny insect flight[J]. Journal of Experimental Biology, 2004,207(17):3073-3088.

[20] Chen Shiyi, Doolen G D. Lattice Boltzmann method for fluid flows[J]. Annual Review of Fluid Mechanics, 1998,30(1):329-364.

[21] Grunau D, Chen Shiyi, Eggert K. A lattice Boltzmann model for multiphase fluid flows[J]. Physics of Fluids A, 1993,5(10):2557-2562.

[22] Fallah K, Khayat M, Borghei M H, et al. Multiple-relaxation-time lattice Boltzmann simulation of non-Newtonian flows past a rotating circular cylinder[J]. Journal of Non-Newtonian Fluid Mechanics, 2012(177-178):1-14.

[23] Lim C Y, Shu Chang, Niu Xiaodong , et al. Application of lattice Boltzmann method to simulate microchannel flows[J]. Physics of Fluids, 2002,14(7):2299-2308.

[24] Pan Chongxun, Luo Lishi, Miller C T. An evaluation of lattice Boltzmann schemes for porous medium flow simulation[J]. Computers & Fluids, 2006,35(8):898-909.

[25] 郭亚丽, 徐鹤函, 沈胜强,等. 利用格子Boltzmann方法模拟矩形腔内纳米流体Raleigh-Benard对流[J]. 物理学报, 2013,62(14):1691-1702.

Guo Yali, Xu Hehan, Shen Shengqiang, et al. Nanofluid Raleigh-Benard convection in rectangular cavity: simulation with lattice Boltzmann method[J]. Acta Physica Sinica, 2013, 62(14):1691-1702. (in Chinese)

[26] Fauci L J. Peristaltic pumping of solid particles[J]. Computers & Fluids, 1992, 21(4): 583-598.

[27] Chrispell J, Fauci L. Peristaltic pumping of solid particles immersed in a viscoelastic fluid[J]. Mathematical Modelling of Natural Phenomena, 2010, 20(5): 67-83.

[28] Connington K, Kang Qinjun, Viswanathan H,et al. Peristaltic particle transport using the lattice Boltzmann method[J]. Physics of Fluids, 2009, 21(5): 711-715.

[29] Waldrop L, Miller L. Large-amplitude, short-wave peristalsis and its implications for transport[J]. Biomechanics and Modeling in Mechanobiology, 2016, 15(3): 629-642.

[30] Liu Feifei, Ren Xiaofei, Wei Shoushui, et al. Bio-inspired micro pump model based on the movement pattern of sperm[J]. International Journal of Hybrid Information Technology, 2016, 9(11): 323-336.

[31] Guo Zhaoli, Shi Baochang, Wang Nengchao. Lattice BGK model for incompressible navier-stokes equation[J]. Journal of Computational Physics, 2000, 165(1): 288-306.

[32] Zhang Junfeng, Johnson P C, Popel A S. Effects of erythrocyte deformability and aggregation on the cell free layer and apparent viscosity of microscopic blood flows[J]. Microvascular Research, 2009, 77(3): 265-272.

[33] Zinner G, Geister B. An extrapolation method for boundary conditions in lattice Boltzmann method[J]. Physics of Fluids, 2007, 14(14): 2007-2010.

[34] Chen Shiyi, Martínez D, Mei R. On boundary conditions in lattice Boltzmann methods[J]. Physics of Fluids, 1998, 8(9): 2527-2536.

[35] Yong K S, Kang J, Kang S. Assessment of algorithms for the no-slip boundary condition in the lattice Boltzmann equation of BGK model[J]. International Journal for Numerical Methods in Fluids, 2008, 58(12): 1353-1378.