基于向量拟合法的配电变压器振动特性分析*

胡 敏， 彭 伟， 金之俭， 袁国刚

(1．上海久隆电力公司变压器修试分公司 上海，200436) (2．国网上海市电力公司电力科学研究院 上海，200437) (3．上海交通大学电子信息与电气工程学院 上海，200240) (4．上海睿深电子科技有限公司 上海，201108)

引 言

随着国民经济发展与城市化进程的推进，配电变压器在各地城区得到广泛的应用。保障这类变压器安全可靠运行已经成为供电部门的重要工作，分析并掌握这类变压器在不同工作状态下的振动特性对于日常巡检和故障诊断有着重要指导意义。自20世纪90年代以来，振动噪声测试与分析方法在电力领域得到普遍采用。丁登伟等[1]通过试验方法采集并分析了调试中的特高压直流输变电系统对于周边交流变压器的振动影响。骆波等[2]采用复Morlet小波辨识变压器绕组的模态参数。顾晓安等[3]应用多普勒激光测振仪和声学测试系统分析变压器铁芯的振动和噪声。

由于配电变压器的振动和噪声本质上是一个包含电场、磁场、流体和结构在内的复杂多物理场耦合作用，单纯依赖数值仿真手段不足以全面把握系统的振动特性且难度很大，相比之下试验方法简便而易行，随之而来的海量数据处理与分析对使用者提出了更高的专业要求。无论是经验模态分析(experimental modal analysis，简称EMA)还是工况模态分析[4](operational modal analysis，简称OMA)都不能很好地满足多测点情况下的数据精细化与自动化分析的要求。文献[5-6]引入了向量拟合法(vector fitting，简称VF)，并初步建立了振动参数自动化与精细化分析的基础框架。向量拟合法[7-9]是一种基于部分分式展开的最小二乘法迭代方法，该方法能够避免同类方法常见的数值病态缺点，并且在滤波器设计、电磁模拟以及医学等多个领域得到推广应用。

笔者应用向量拟合法与频域复指数最小二乘法(PolyLSCF)对圆筒结构进行振动特性分析，并应用该方法分析配电变压器在工作状态下的振动数据。

1 向量拟合法原理

向量拟合法首先将系统频响函数H(s)假定为有理多项式的部分分式展开

(1)

其中：a为频响函数极点；p为留数；d和e为常系数。

接着设定初始极点并引入权重函数Θ(s)得到式(2)，那么权函数与系统频响函数的乘积同样可以用有理多项式的部分分式展开为式

由式(1)、式(2)和式(3)可以得到

(4)

将频响函数H(s)的Ns个频域点代入式(4)，可以得到一个线性最小二乘计算公式

Aix=bi

(5)

其中：i=1,2,…,Ns；Ns为频域采样点个数；bi=F(si)为测试值。

(6)

求解的未知量

(7)

将全部测试数据代入后，可以得到

(8)

式(8)可以通过QR方法进行数值求解获得各项系数，那么权函数Θ(s)和Θ(s)H(s)的近似结果可以表示为

系统的频响函数可以写成

(9)

向量拟合法的主要优点是分子与分母可以选择不同的多项式阶次来适应不同类型的分析模型，增加模型阶次为噪声提供出口的同时保证算法的稳定性与鲁棒性。

向量拟合法算法的过程如下：

1) 设定分析对象的多项式起止阶次以及最高迭代次数；

2) 寻找响应曲线的主要峰值点，并设为初始极点；

3) 迭代循环计算，当迭代次数达到最高迭代次数或者拟合曲线的频响函数置信度达到预定时，退出本轮循环；

4) 若达到最高阶次则退出，否则将计算结果补充新的初始极点后，回到步骤3。

算法步骤3中间的频响函数置信度(frequency response assurance criterion，简称FRAC)的具体定义为

其中：Htest(ω)和Hfit(ω)分别为测试与拟合频响函数；星号表示共轭转置。

根据实践经验，建议频响函数置信度可以设定在0.95～0.99之间，同时极点数目应当比频响函数的谱线数至少低一个数量级，从而避免过拟合现象发生。

2 向量拟合法有效性验证

为了验证向量拟合法对配电变压器振动数据分析的有效性，笔者选取了与配电变压器外壳具有一定几何相似性的圆筒结构的振动测试数据作为验证用算例，采用频域复指数最小二乘法的模态频率和阻尼结果作为参照。圆筒测点布置图见图1，沿圆周方向合计13个测点，选择#1作为参考点。图2为#1的时域加速度响应， 采样频率为8 kHz，采样时间为36.4 s。频域复指数最小二乘方法的模型阶次设定为15～90，同时为了验证向量拟合法的数值稳定性和鲁棒性，模型阶次设定为40～320。

表1列出了两种方法辨识得到的模态频率和阻尼，可以看出向量拟合法与频域复指数最小二数法的结果吻合很好。从图3和图4对比可以发现，向量拟合法的模型阶次在高达320的情况下，仍然能够保证数值稳定性和鲁棒性。

图1 测点布置示意图Fig.1 Test points setting

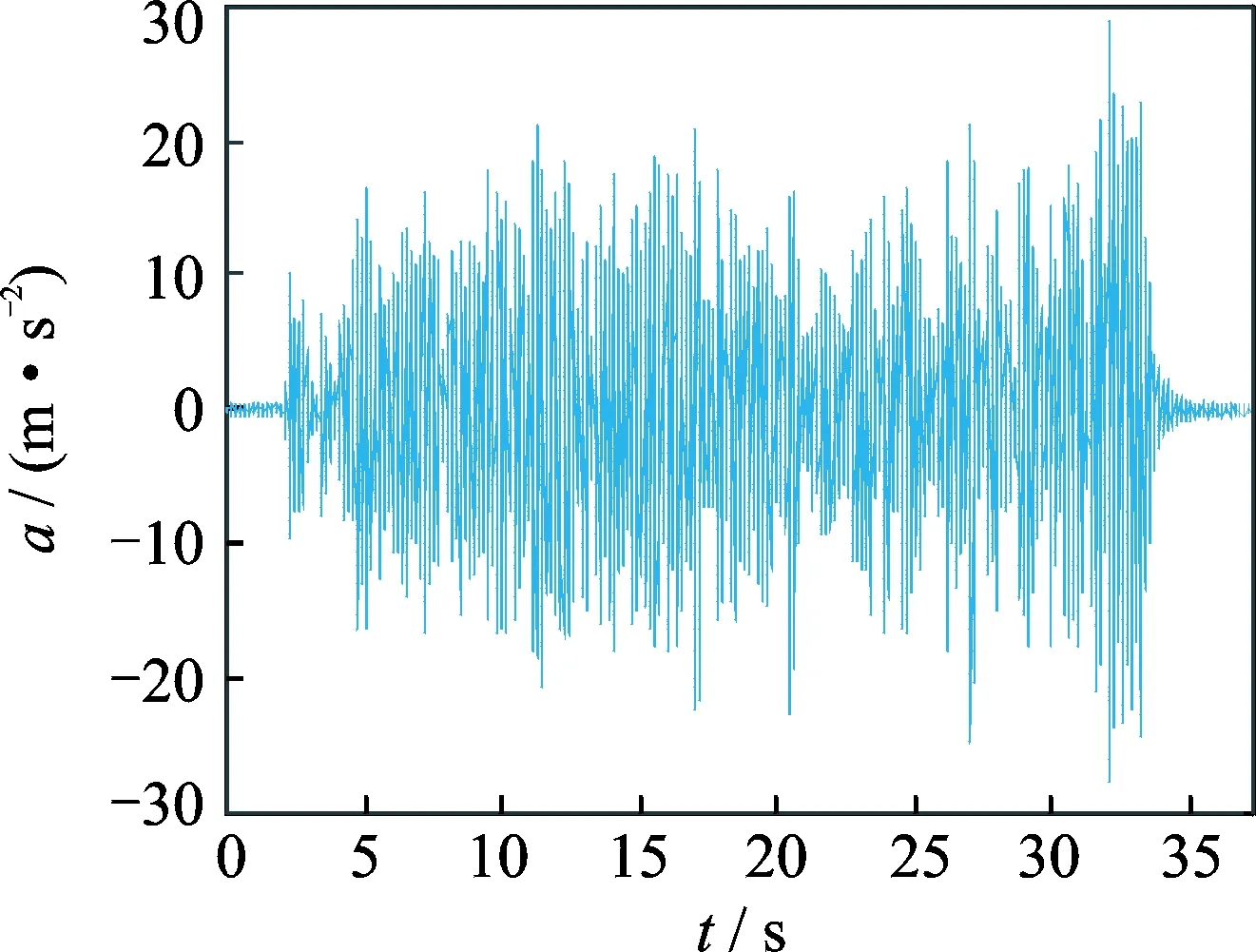
图2 测点1的时域响应Fig.2 Point 1 time-domain response

定义曲线拟合误差公式以便比较向量拟合法的拟合结果误差。

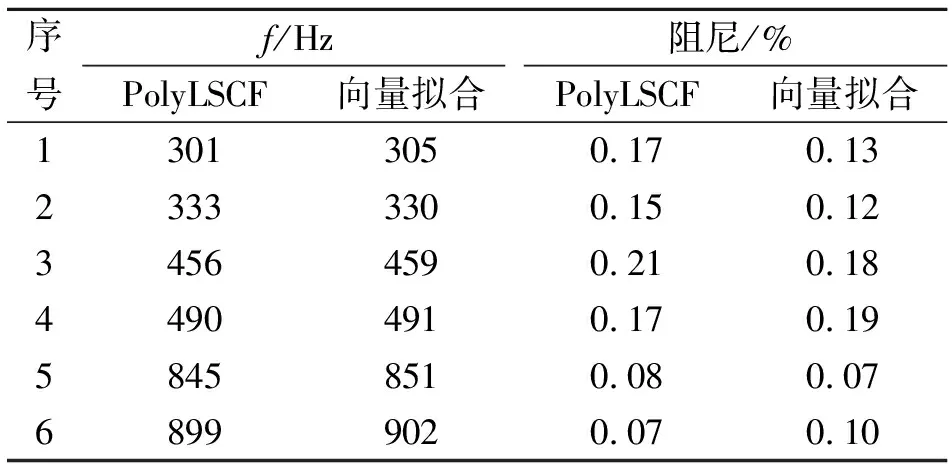
表1 两种方法结果对比

图3 频域复指数最小二乘法的稳定图Fig.3 Stable diagram of VF

图4 向量拟合法的稳定图Fig.4 Curve of fitted FRFs

(10)

其中：Fmeasure为测试数据；Ffit为拟合结果。

由图5可以看出，随着模型阶次的增加，向量拟合法的拟合误差迅速下降，最低可以达到48 dB，再次表明该方法良好的数值稳定性和鲁棒性。这一特性能够降低对使用者相关专业知识和经验的要求。

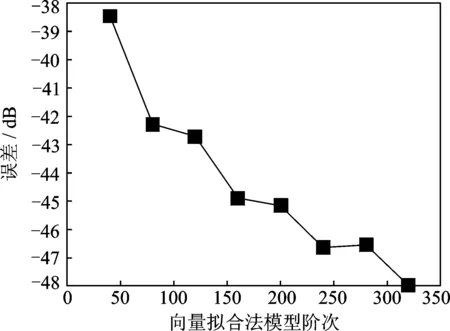
图5 拟合误差曲线Fig. 5 Curve of fitted FRFs

3 试验分析

配电变压器在屏蔽消声室环境中进行振动测试，试验对象为上海忠久变压器公司的S11-320/10油浸变压器，额定电压为10/0.4 kV，额定电流为18.48/462 A。

振动测量采用36个加速度传感器，将变压器的4个表面分为均匀的网格，其中高压侧和低压侧分别布置了12个测点，左右两侧分别布置了6个测点，测量箱壁上的法向振动。试验项目为了其他试验目的加装了4个噪声测点同步测量噪声信号，变压器工况采用额定空载状态进行试验，测点布置与变压器实物如图6、图7所示。

图6 试验装置图Fig.6 Power transformer for testing

图7 试验测点图Fig.7 Setting of test points

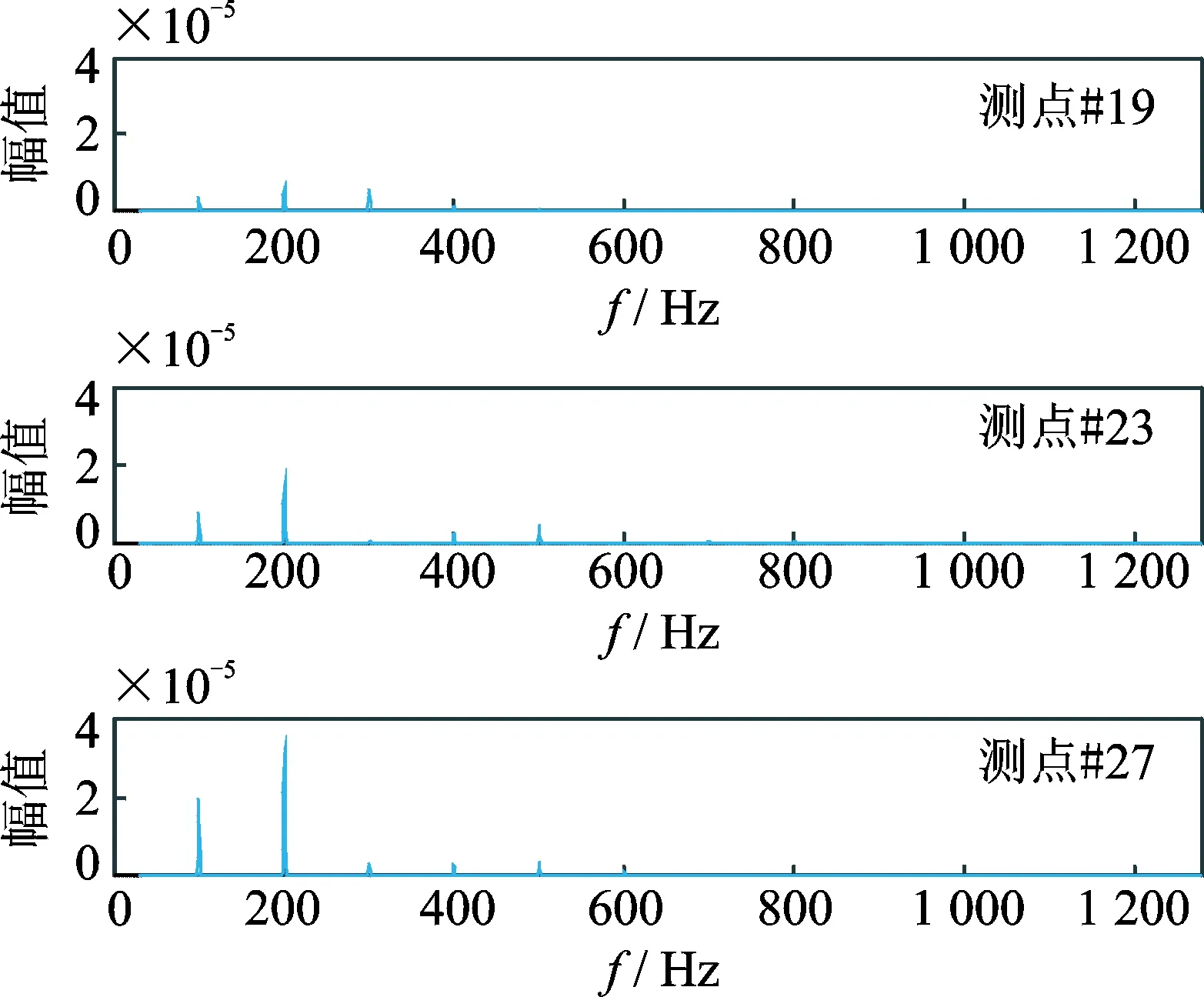
图8 测点#19，#23和#27自功率谱Fig.8 Test point #19, #23 and #27 auto power spectrum

图9 测点#13，#15和#17自功率谱Fig.9 Test point #13, #15 and #17 auto power spectrum

首先对全部36个测点的振动测试数据进行降噪和平滑的预处理，然后计算得到功率谱矩阵。从变压器高压自顶向下选择#19，#23和#27，从变压器侧边自顶向下选择#13，#15和#17，通过上述点的自功率谱数据图8和图9对比，可以看出变压器100 Hz的工作频率及其倍频引起的强迫振动响应占据主导地位，在600 Hz以上的频率段内强迫振动响应衰减明显。位于变压器底部的响应要明显高于顶部的响应，这是由于在空载状态下变压器的主要振动源是铁芯，而变压器箱壁底部与铁芯直接通过底脚螺栓连接固定，造成变压器底部的振动量级更大。

接着用向量拟合对全部测点的振动数据进行分析，分析频率为0～640 Hz，模型阶次从50增长到500，图10为向量拟合法得到的稳定图。由图11可看出，随着向量拟合法的模型阶次逐步增加，拟合曲线的误差迅速下降并保持稳定。

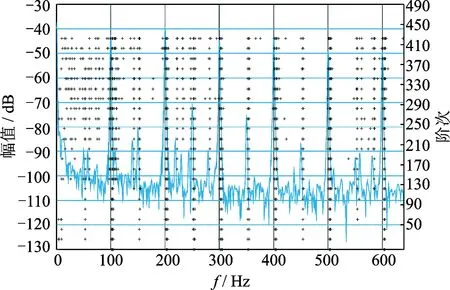
图10 稳定图Fig.10 Stable diagram

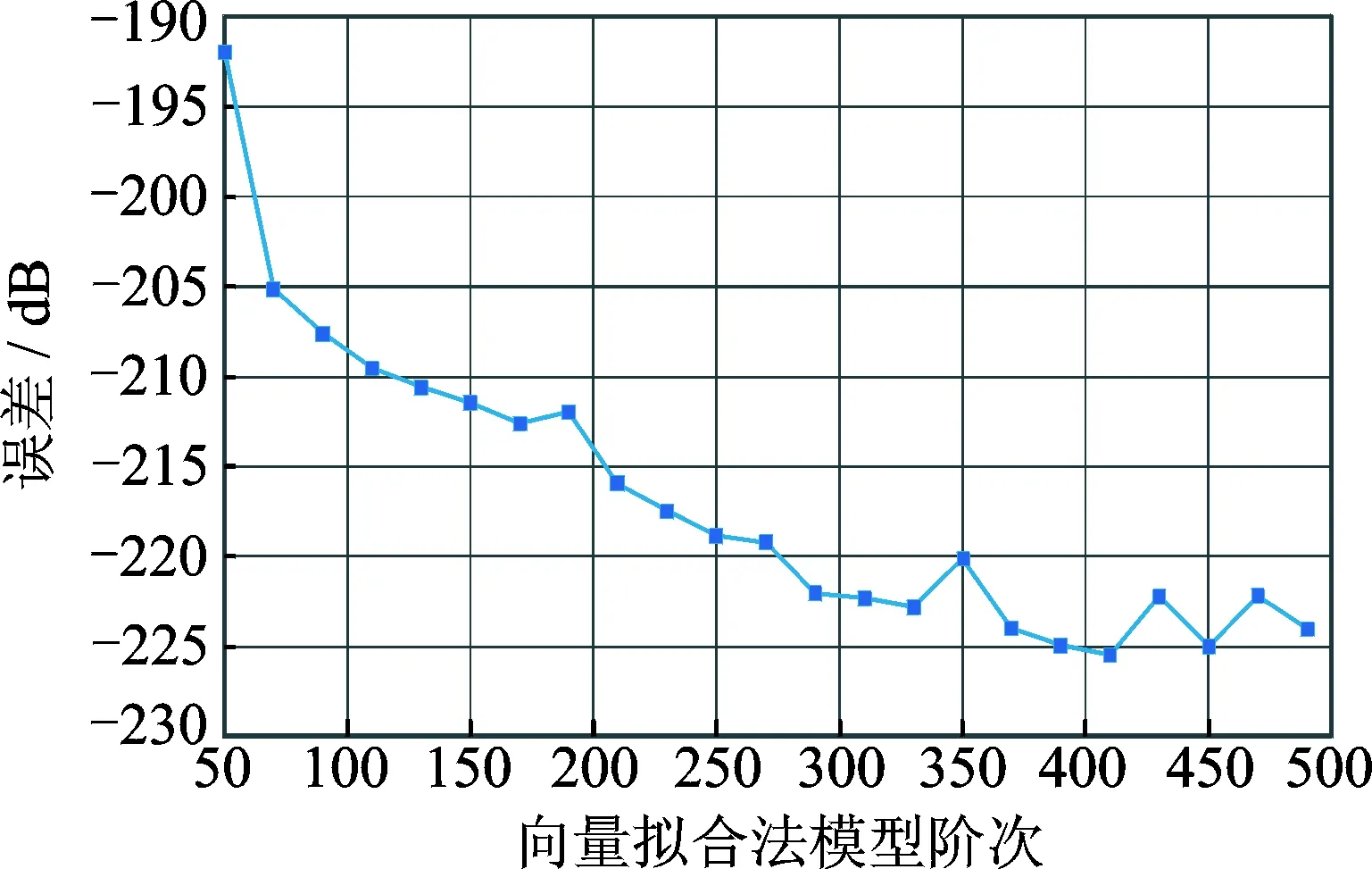
图11 变压器拟合误差曲线Fig.11 Curve of transformer′s fitted FRFs

通过分析得到了表2所示的100 Hz工作频率及其倍频引起的虚假模态频率以及表3所示的系统的模态频率和阻尼，可以看出，这些激励频率对应的阻尼比低于0.01%，通过判断阻尼比能够辨识出虚假模态。

表2 激励引起的虚假模态

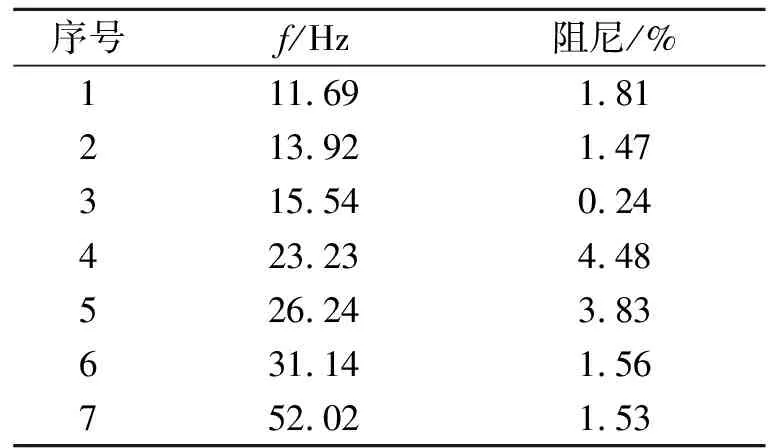
表3 系统的模态频率和阻尼

对于变压器壳体底部的振动量级较大的#35和#36测点数据单独使用向量拟合法进行振动特性的精细化分析，模型分析阶次从40到300。通过阻尼比筛选剔除激励引起的虚假模态后，发现41.4 Hz处可能存在1阶局部模态。进一步分析试验数据，发现由于变压器顶部测点#31和#32在该频率处的振动量级10-10g远小于底部测点#35和#36振动量级10-6g，故在整体分析中该阶模态完全有可能因为振动能量太小而被噪声信号掩盖，在后续工作中需要借助测试与仿真手段对此深入研究。由图12可看出，曲线拟合法能够很好地拟合测试数据，拟合误差比测试数据要小1～2个量级,所以在变压器振动测试和故障诊断中，底部的振动量级大。通过向量拟合法能够辨识出可能的局部模态，并能很好地拟合测试曲线，可以为测点的优化和故障诊断提供参考依据。

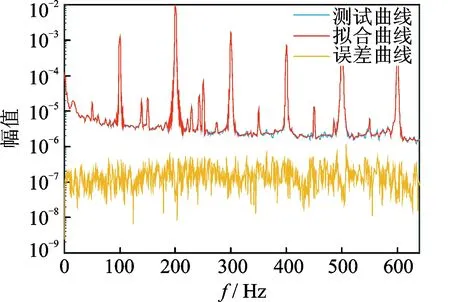
图12 测点#36的拟合结果对比Fig.12 Test curve and fitted curve of point #36

4 结束语

通过单独对变压器壳体底部振动量级较大的部分测点进行拟合分析发现，拟合曲线和测试数据吻合很好，误差比测试数据小1～2个数量级，并辨识出底部存在1阶局部模态，因此可以通过变压器的工作状态提取其模态参数。向量拟合法可以用于分析配电变压器的振动特性，其特点为：a.识别的稳定性更高，在高阶次仍然有比较好的鲁棒性；b.可以快速剔除由于受迫振动造成的虚假模态。模态参数对应着试验对象的动力学特征，可以将向量拟合法进一步应用在变压器的振动测点布置优化或者降低测点数，从而简化振动测量的工作量，并且通过局部的模态特征识别可以和内部特征变化对应起来进行深入研究。

参 考 文 献

[1] 丁登伟,张星海,兰新生. HVDC单极运行对500kV交流变压器的振动影响分析研究[J]. 振动与冲击, 2016,35(17):201-206.

Ding Dengwei,Zhang Xinhai,Lan Xinsheng. Effect investigation of vibration on 500kV AC transformer caused by HVDC system under monopole operation[J]. Journal of Vibration and Shock,2016,35(17): 201-206.(in Chinese)

[2] 骆波,王丰华,廖天明,等. 应用改进复Morlet小波识别电力变压器绕组模态参数[J].振动与冲击,2014,33(6): 131-136.

Luo Bo, Wang Fenghua, Liao Tianming,et al. Modal parameters identification of power transformer winding based on the improved complex Morlet wavelet[J]. Journal of Vibration and Shock,2014,33(6):131-136.(in Chinese)

[3] 顾晓安,沈密群,朱振江,等. 变压器铁心振动和噪声特性的试验研究[J].变压器,2003,40(4):1-4.

Gu Xiaoan, Shen Miqun, Zhu Zhenjiang, et al. Test research on vibration and noise level in transformer core[J]. Transformer,2003,40(4):1-4.(in Chinese)

[4] 秦飞,宋汉文,王文亮. 基于现代谱估计理论的工况模态分析[J]. 振动与冲击,2002,21(4):74-79.

Qin Fei, Song Hanwen, Wang Wenliang. Operational modal identification on modern spectral estimation[J]. Journal of Vibration and Shock, 2002,21(4):74-49. (in Chinese)

[5] 董磊,宋汉文,郑铁生. EMA与OMA模态参数辨识统一性方法[J]. 振动与冲击,2016,35(12):7-12.

Dong Lei, Song Hanwen, Zheng Tiesheng. Unity method for EMA and OMA in frequency domain[J]. Journal of VIbration and Shock, 2016, 35(12):7-12. (in Chinese)

[6] 董磊,宋汉文,郑铁生. 频响函数曲线拟合与模态分析精细化[J]. 振动与冲击, 2016,35(2):69-75.

Dong Lei，Song Hanwen，Zheng Tiesheng. The refinement of FRFs curve fitting and modal analysis[J]. Journal of Vibration and Shock, 2016, 35(2):69-75. (in Chinese)

[7] Gustavsen B, Semlyen A. Rational approximation of frequency domain responses by vector fitting[J]. IEEE Transactions and Power Delivery,1999,14(3):1052-1061.

[8] Zeng R,Sinsky J.Modified rational function modeling technique for high speed circuits[C]∥International Microwave Symposium Digest. San Francisco, California, USA:[s.n.],2006:1951-1954.

[9] Robinson S R, Nguyen C T,Allen J B. Characterizing the ear canal acoustic reflectance and impedance by pole-zero fitting[J]. Hearing Research, 2013, 301(1):168-182.