转子系统支承松动故障非线性参数识别*

曹树谦， 黄亚明

(1.天津大学力学系 天津，300072) (2.天津市非线性动力学与混沌控制重点实验室 天津，300072) (3.天津大学内燃机燃烧学国家重点实验室 天津，300072)

引 言

在航空发动机中存在着不可忽视的非线性结构参数和物理参数(如间隙、刚度、阻尼等)，特别是故障发生以后，故障部位结构和物理参数会发生较大变化，其动力学特性随之发生根本性变化。支承松动故障是对航空发动机等旋转机械危害较大的故障。转子系统由于安装质量不高、固定螺栓强度不够以及在长期、周期性振动的作用下导致转子系统支承结合面紧力不足或间隙过大，从而引发松动故障，降低了系统刚性，从而加剧其振动响应，甚至造成重大经济损失[1-5]。对松动故障转子的参数识别，可为以后建立反映实际工程问题的模型提供理论依据，为故障的监控与诊断提供一种新的思路。

参数识别是动力学反问题，近年来，优化算法被越来越多地运用到这类问题中[6-10]。遗传算法作为一种智能优化算法有着良好的全局搜索性能，即使在所定义的适应度函数不连续、非规则或有噪声的情况下，也能以很大的概率找到全局最优解[11]。

笔者将支承松动故障参数识别问题转化为参数优化问题。针对传统遗传算法存在着早熟收敛的问题，改进了算法中新一代种群的生成机制。父代种群进行交叉与变异操作后，并不直接产生新一代种群，而是取父代种群与生成的种群中适应度排序靠前的个体组成新一代种群。这样，遗传算法可以较大的概率进行变异，提高新个体产生的速度，而不至于破坏父代种群中的优秀个体。利用该方法，识别了支承松动故障转子-滚动轴承系统的故障非线性参数。通过与传统遗传算法识别结果的比较，证明了改进的有效性。通过研究不同变异率对识别结果的影响，说明了大的变异率不会破坏改进遗传算法的遗传模式。研究了不同噪声强度对改进遗传算法识别结果的影响，并利用该遗传算法开展了基于实测信号的参数识别，对识别结果的可靠性进行了分析。

1 支承松动故障转子-轴承系统动力学方程

1.1 转子系统动力学模型

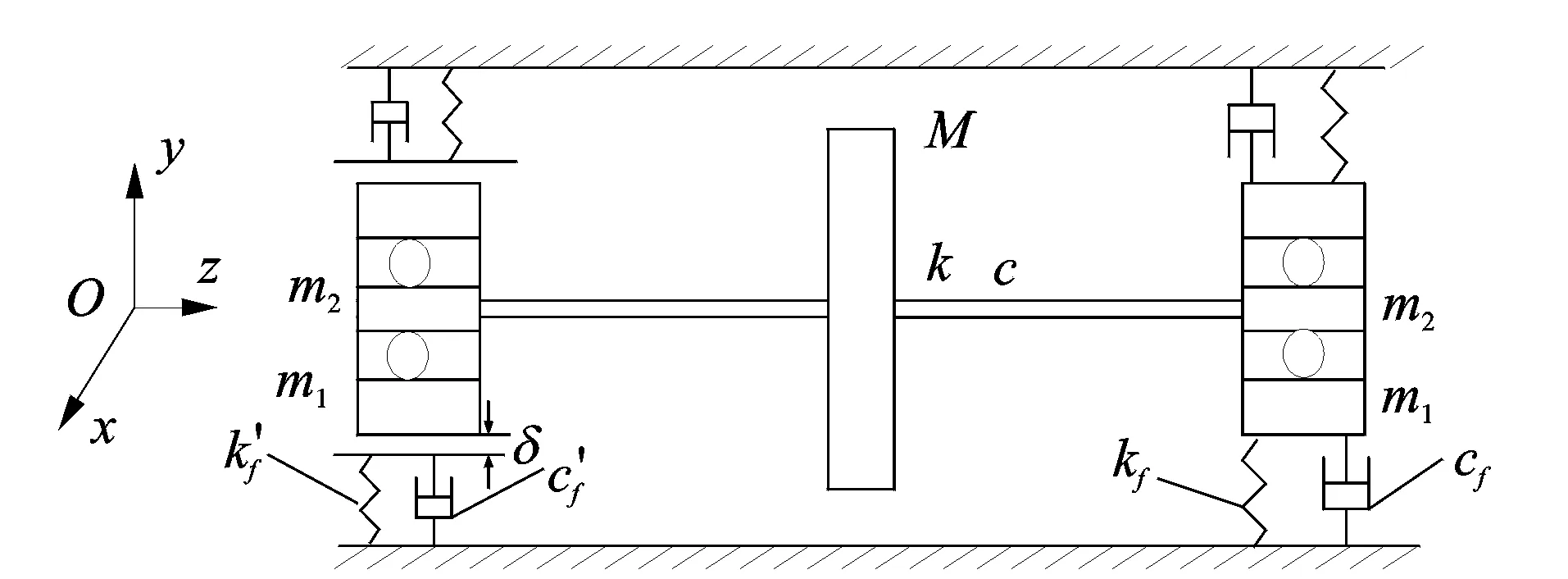
图1 支承松动转子-轴承系统动力学模型Fig.1 Rotor-bearing system with pedestal looseness

1.2 动力学方程

设x1,y1分别为右端支座形心在x,y方向的坐标，x2和y2分别为右端轴心在x，y方向的坐标，x3和y3分别为转盘形心在x，y方向的坐标，x4和y4分别为左端轴心在x，y方向的坐标，x5和y5分别为左端支座形心在x,y方向的坐标。

转子系统的动力学微分方程可以表示为

(1)

其中：ω为转子转速；g为重力加速度。

当支座发生松动故障时，松动端的刚度和阻尼由于松动间隙的影响而视为分段线性[12-13]

(2)

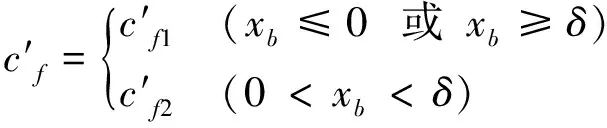
(3)

其中:xb为支座的位移，刚度与阻尼在水平和铅直方向的计算公式相同。

Fx1和Fy1分别为未松动端轴承力在x，y方向上的分量，Fx4和Fy4分别为松动端轴承力在x，y方向上的分量。图2为滚动轴承模型，滚珠在内外滚道间等距排列，滚珠与滚道之间保持纯滚动。

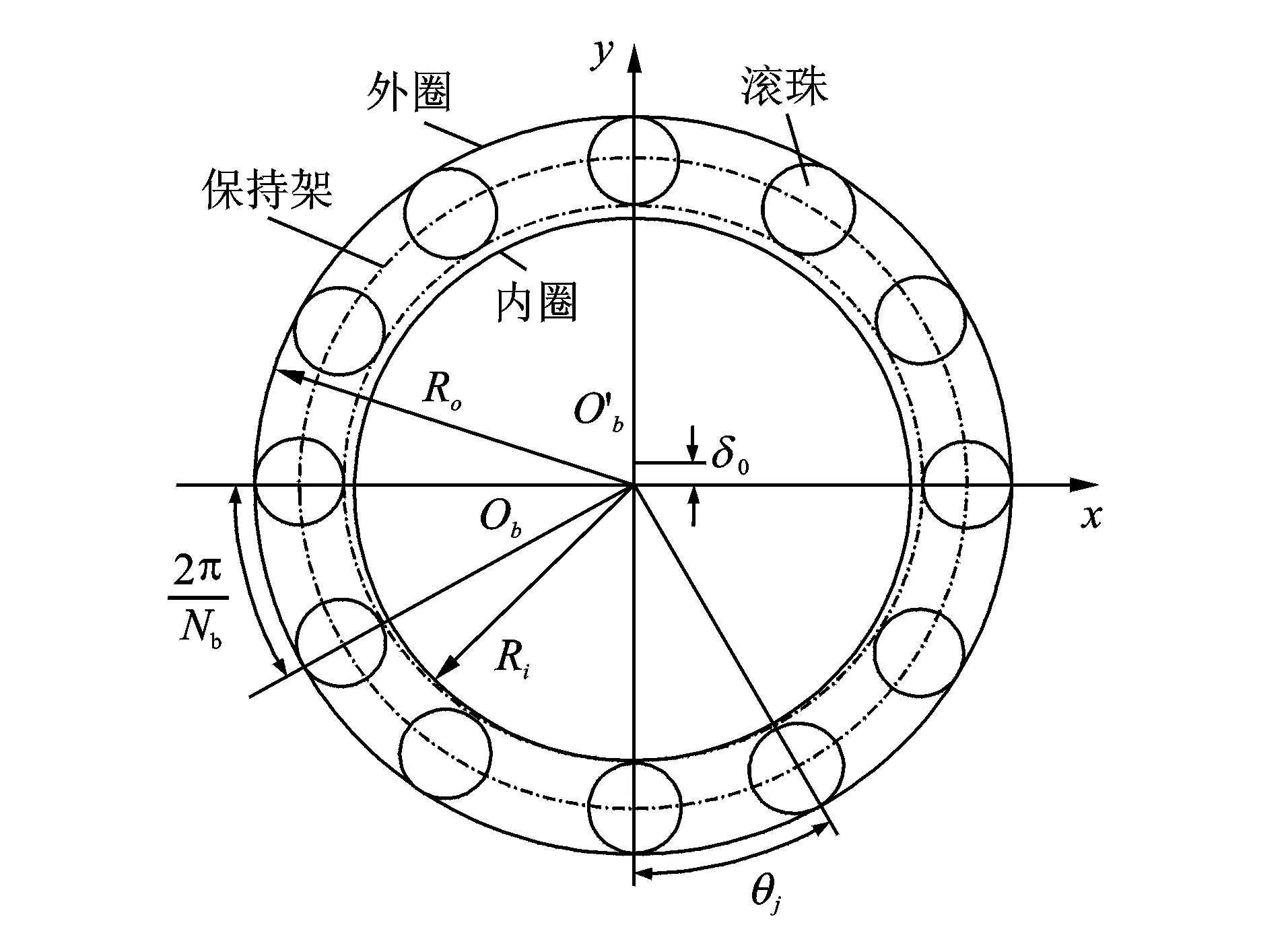
图2 滚动轴承模型Fig.2 Ball bearing model

该转子模型中，滚动轴承外圈固定，内圈固定在转子上，参考文献[14-15]，则轴承力可表达为

其中：Nb为滚珠个数；Kc为赫兹接触刚度；x，y分别为轴承形变在水平与铅直方向的分量；δ0为轴承初始间隙；H(·)为亥维赛函数；θj为滚动轴承在第j个滚珠处的角度。

(6)

其中：ωcage为保持架的转速。

设外圈半径为R，内圈半径为r，则

ωcage=ωr/(R+r)

(7)

由此可得式(1)中轴承力为

(8)

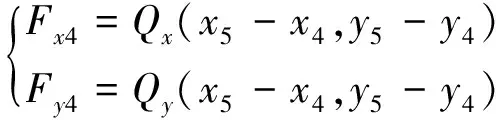
(9)

2 基于改进遗传算法的参数识别方法

遗传算法是一种启发式的搜索算法，它将达尔文进化论的自然选择和遗传机制引入计算模型中，通过模拟生物自然进化过程搜索最优解。在寻优过程中，按照所选择的适应度函数，通过遗传中的选择、交叉和变异对个体进行筛选，使适应度值好的个体被保留，适应度差的个体被淘汰，体现了自然进化过程中的“优胜劣汰、适者生存”的生物进化原理。每一代新的群体既继承了上一代的信息，又优于上一代，这样反复循环，直至满足条件。

传统遗传算法存在着致命的早熟收敛缺陷，种群中个体的多样性过早缺失，使进化陷于停滞。为保证遗传进化过程中个体的多样性，可以适度提高种群变异概率，但是这样又会破坏遗传算法的稳定性。为解决这一问题，笔者对传统遗传算法的遗传过程进行了一些改进。父代种群进行交叉与变异操作后，并不直接产生新一代种群，而是取父代种群与生成的种群中适应度排序靠前的个体组成新一代种群，这样不仅可以避免父代种群中优秀的个体在遗传过程中丢失，而且还会大大提高种群的进化速度。利用改进的遗传算法识别支承松动参数的具体步骤如下。

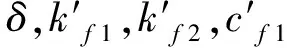
2) 产生初始种群。随机产生N个实数串，组成初始种群G0。

3) 适应度评价。适应度是遗传算法中评价染色体优劣的指标，一般应为非负函数，遗传算法的迭代搜索总是以适应度最大为目标。将目标函数映射为基于参数识别方程计算的位移响应与实测振动位移响应之间的误差函数，即可用两响应之间方差和来描述参数的优劣程度。误差函数越小，适应度越大。为了避免过早收敛与函数运算出错，取定标后的适应度函数为

F(xk)=-log(Ek+Cm)

(10)

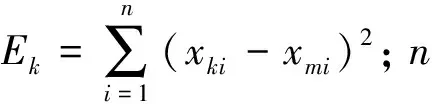
4) 选择。用放回取样的方法从种群中选出N个个体组成父本，本研究采用基于适应度比例的轮盘赌法选择策略，每一次选择中，第k个个体被选中的概率为

(11)

其中：s为种群中个体的数目。

5) 交叉。采用实数交叉法，第k条染色体ak和第l条染色体al在j位的交叉方法如下

(12)

其中：b为[0 1]之间的随机数。

6) 变异。设第i条染色体的第j个基因aij发生变异，变异前先随机产生一个[0 1]间的随机数r，则变异方法如下

(13)

其中：amax为基因aij的上界；amin为基因aij的下界；f(g)=r2(1-g/Gmax)2；g为当前迭代次数；Gmax为最大迭代次数；r2为[0 1]间的随机数[16-17]。

7) 为了避免种群中优秀个体经交叉与变异后消失，对生成的新种群进行适应度评价，并将新种群与父本中的个体合并，并按适应度进行排序，取适应度靠前的N个个体组成新一代种群。

8) 重复步骤4～7，直至完成设定的迭代次数。

3 基于改进遗传算法的支承松动参数识别

对于图1所示的支承松动转子-轴承系统，其基本参数为：M=8 kg，e=0.06 mm，k=2.7×106N/m，c=4×102(N·s)/m，m1=1kg，m2=2 kg，kf=1×107N/m，cf=9×102(N·s)/m。滚动轴承型号为JIS6306，其参数见表1。设系统左端支座出现了松动故障，松动参数如表2所示。取转速ω=500 rad/s，用四阶龙格-库塔法对式(1)进行数值积分，采样频率为每周期100个点，取松动端轴心y方向位移响应的10个稳定周期数据作为输入信号进行参数识别，输入信号如图3所示。

表1 滚动轴承参数

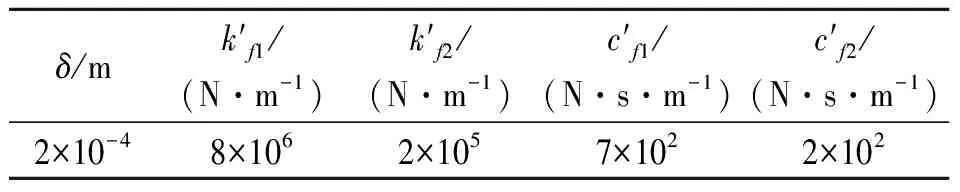
表2 支承松动参数

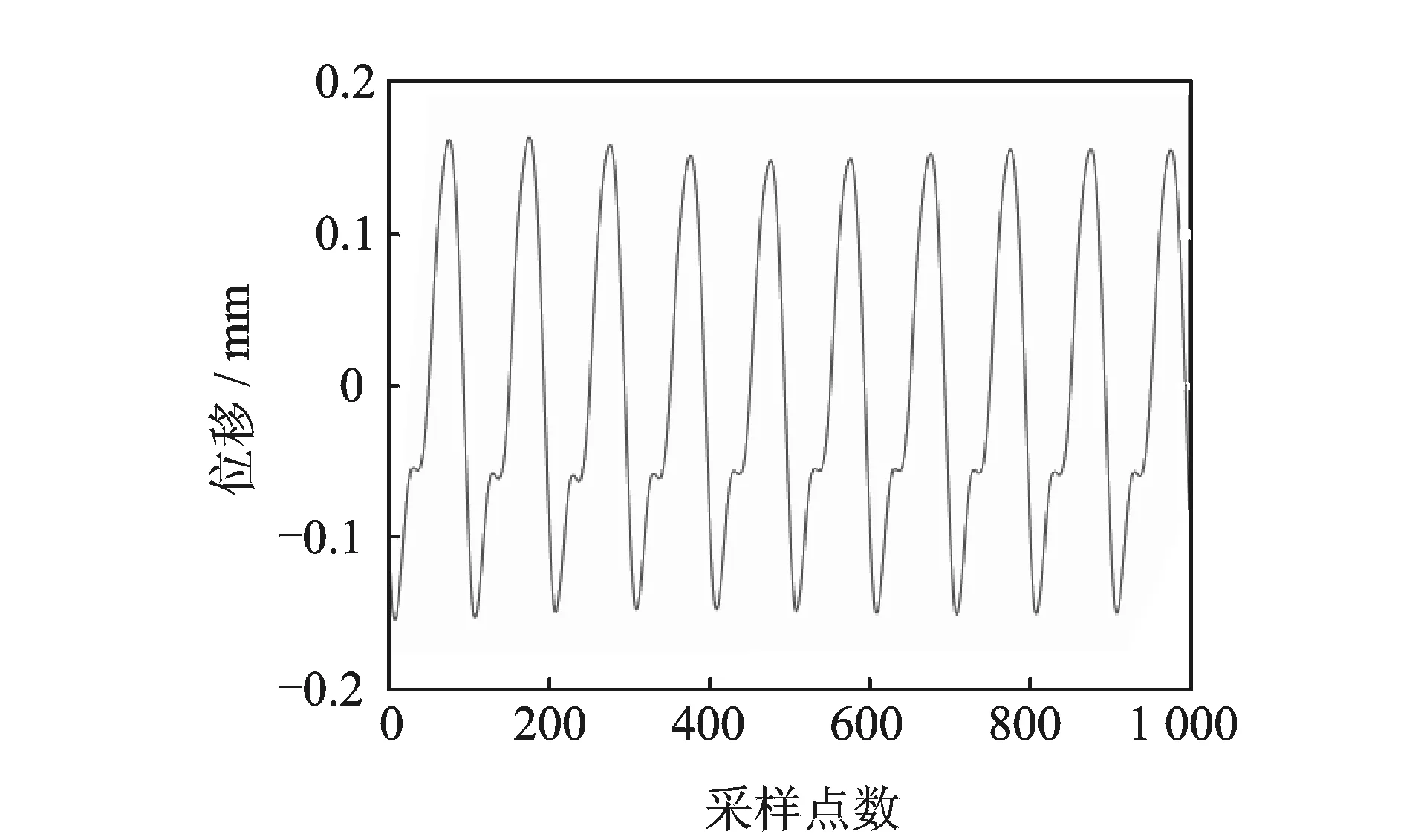
图3 松动端轴心y方向的位移响应曲线Fig.3 Displacement of the looseness shaft end in the y direction

3.1 改进遗传算法与传统遗传算法识别结果比较

取遗传算法计算参数：种群规模为100，交叉率为0.8，变异率为0.1，迭代次数为200，分别利用传统遗传算法和改进的遗传算法对支承松动参数进行识别。由图4可知，传统遗传算法出现了早熟收敛情况，迭代到70代以后，误差函数几乎不再减小，进化基本上陷入停滞；而改进的遗传算法大大提高了种群的进化速度，在相同的遗传参数条件下，改进的遗传算法更快地向目标值收敛，而传统遗传算法的早熟收敛情况也得到了解决。表3为两种遗传算法对松动参数的识别结果，在经过200代的进化后，传统遗传算法与改进遗传算法识别结果的误差函数分别为4.850 0×10-7m2与1.518 3×10-9m2，说明改进遗传算法的识别精度远远高于传统遗传算法。传统遗传算法识别结果的最大误差高达110.10%，改进遗传算法识别结果的最大误差为15.57%。

图4 改进遗传算法与传统遗传算法误差函数曲线Fig.4 The error function curves of the improved algorithm and the traditional algorithm

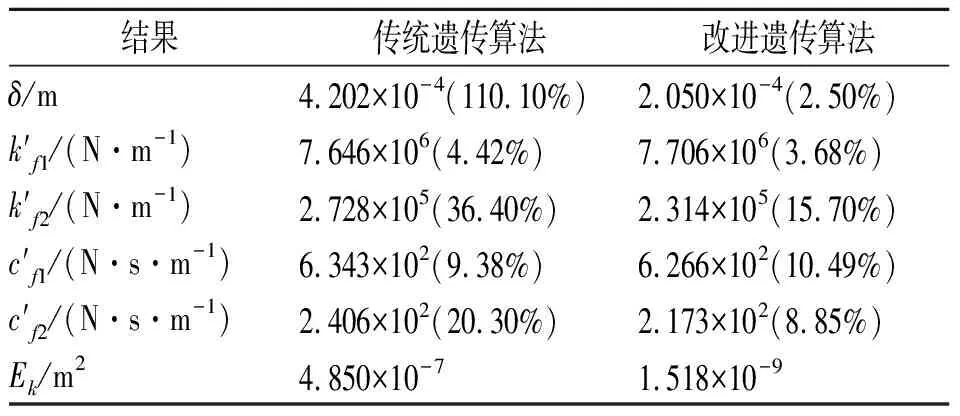
表3 改进遗传算法与传统遗传算法的识别结果比较

3.2 变异率对改进遗传算法识别结果的影响

传统遗传算法的变异率一般取值为0.000 1～0.1，以期获得最佳的识别效果。改进的遗传算法能以相对较大的概率进行遗传进化。为了确定改进遗传算法变异率的最佳取值，研究了不同变异率下的支承松动参数识别结果。图5为改进遗传算法的识别结果随变异率的变化情况。图5(a)为不同变异率下识别结果的误差函数，经多项式拟合成误差函数随变异率的变化曲线，反映总体的识别精度，误差函数越小，识别精度越高。从图中可以看出，变异率从0增加到0.3，误差函数逐渐减小，表示识别精度随变异率的增大而提高；变异率从0.3到1，误差函数拟合曲线波动很小，可近似看作平行于横坐标轴的直线，这说明变异率大于0.3后，总体的识别精度将不受变异率的影响。图5(b～f)分别为各项参数的识别结果。从图中可以看出，各项参数的识别结果随变异率的变化与误差函数随变异率的变化基本一致。随着变异率的增大，识别结果先是快速向真实值趋近，说明识别精度随变异率的增大而提高；变异率大于0.3后，识别结果只做小幅波动，近似平行于表示真实值的直线，表明识别精度不再随着变异率的增大而提高。由此可知，变异率取0.3时，改进遗传算法性能达到了其最佳值；当变异率大于0.3时，识别精度并没有随之下降，说明大的变异率不会破坏改进遗传算法的遗传模式,该方法仍能有效地识别支承松动的故障参数。

3.3 噪声对改进遗传算法识别结果的影响

在实际测试中系统受到噪声干扰，因此在响应信号中加入不同强度的白噪声来模拟实测信号，考察改进遗传算法的抗噪能力。识别结果如图6与表4所示。从图6中可以看出，随着噪声强度的增大，误差函数收敛到的值也越大，说明噪声会降低识别结果的精确度。表4为不同噪声条件下各个参数的识别结果，就某个参数而言，其精度并不严格地随着噪声强度的增加而降低，这是由于该方法是以各个参数综合影响的响应信号为优化目标，从误差函数可以看出，整体的精度是随着噪声强度的增加而降低的。从表中可以看出，当噪声强度不大于10%时，各个参数的误差均小于30%，说明该遗传算法具有良好的抗噪声能力。

4 基于实测信号的转子支承松动参数识别

实测信号采集于自行设计的多功能转子实验台，该实验台为模块化设计，通过不同部件的组装可开展支承松动实验、双盘不对称转子振动实验、轴承故障实验及螺栓法兰连接实验。本实验基于其松动支承模块，如图7所示。该装置由转盘、转轴以及两端的支承轴承与支座组成，其中左侧支座通过螺栓紧固，右侧出现松动。转子由电机驱动，转速可以由调速器控制。通过电涡流传感器测量松动轴端的振动信号，振动信号通过前置器传输到TST5912动态信号测试分析系统，利用泰斯特测试软件对振动信号进行采集与处理。实验装置参数如表5所示。

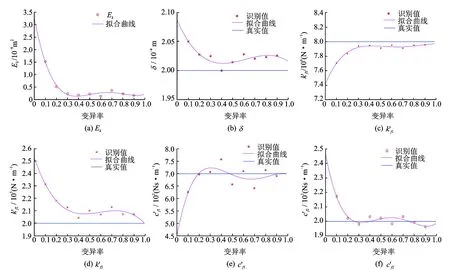
图5 改进遗传算法的识别结果随变异率的变化曲线Fig.5 The curves of identification results with mutation rates

表4 不同噪声条件下改进遗传算法的识别结果

图7 支承松动实验装置Fig.7 Supporting looseness test rig

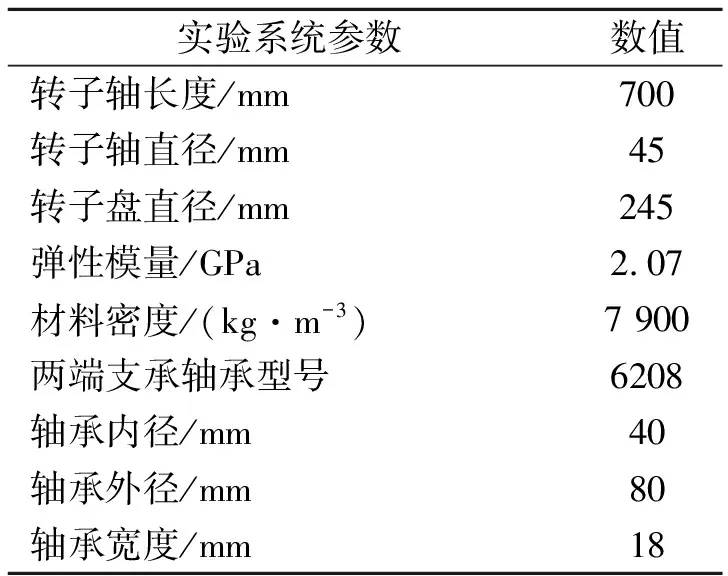
表5 实验系统参数

4.1 支承松动模型

图8为转子系统的支承松动端，在支座与基础之间的紧固螺栓上套上1根弹簧，通过松紧螺栓螺母使支座与基础间产生一个间隙δ，这样，刚性基础底座、弹簧、螺栓及松动间隙等因素构成了分段线性刚度支承。该支承刚度可表示为

(14)

其中：kp≫ks。

通过松紧螺栓螺母，可以定性调节松动间隙的大小。

4.2 实测信号采集

设置测试系统采样频率为10 kHz，电机转速为40 Hz(251.2rad/s)，开机运行待系统稳定后开始采集数据。由于环境中存在高频噪声对信号的干扰，在测试软件中利用低通滤波器对测试信号进行滤波处理。图9分别为松紧程度不同的两种情况下轴端铅直方向上的位移信号。

4.3 基于实测信号的支承松动参数识别

基于这两组振动信号，分别取10个整周期的信号利用改进遗传算法进行参数识别，识别结果如表6所示。

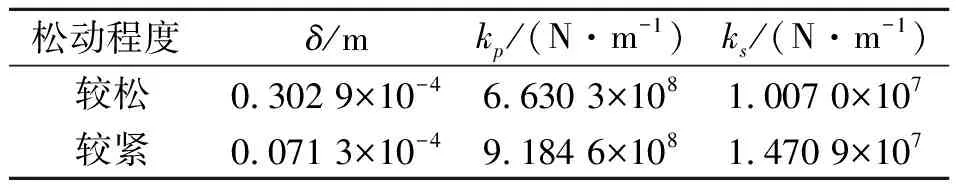
表6 基于实测信号的支承松动参数识别结果

图9 松动端铅直方向实测信号Fig.9 The measured signal of the loose shaft end in the vertical direction

从表6识别结果可以看出，当螺栓连接较紧时，间隙的识别结果明显比较松时小，前者是后者的23.54%。kp和ks的识别刚度都有所增大，分别增加了38.5%和46.8%，这是由于当间隙较小时，在振动过程中螺栓也会产生张紧力而使刚度的值增大。两种松动程度下，kp和ks的比值相差不大，分别为61.96和62.44，均满足kp≫ks。综上所述，基于实测信号的改进遗传算法对转子支承松动参数识别结果有一定的合理性。

为进一步验证基于改进遗传算法对转子支承松动参数识别的可靠性，将通过改进遗传算法识别出的松动参数代入该实验台的模型方程中，获得一组仿真信号，将该仿真信号与实验台实测信号进行比较。图10所示为当转子转速为30 Hz (188.4 rad/s)时，较松与较紧两种情况下各自仿真信号与实测信号的对比。

图10(a),(b)中较松情况下仿真信号位移响应与实测位移响应振动幅值相近，前者为47.36μm，后者为66.1456μm，误差为28.4%。由频谱图可看出，仿真信号与实测信号频谱图中均有2倍频、3频谱等高频成分，而1倍频的幅值分别为12.21和13.99 μm，误差仅为12.6%，仿真信号与实测信号的误差主要来自于振动测试误差与模型简化产生的误差。总体看来，仿真信号能够近似贴合实测信号，说明识别结果的合理性。图10(c),(d)较紧情况下仿真信号与实测信号的比较相类似。

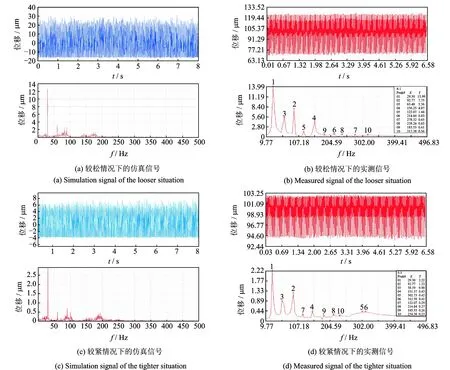
图10 仿真信号与实测信号的比较Fig.10 The comparison of simulation signal and measured signal

5 结 论

1) 当种群规模为100、交叉率为0.8、变异率为0.1时，传统遗传算法迭代到70代以后，进化就陷入了停滞，出现了早熟收敛问题；而改进的遗传算法较好地解决了早熟收敛问题，经过200次迭代后，改进遗传算法的识别精度大大高于传统遗传算法。

2) 当变异率小于0.3时，随着变异率的增大，识别结果先是快速向真实值趋近，识别精度逐渐提高;当变异率大于0.3后，随着变异率继续增大，识别精度不再提高，说明在变异率取0.3时，改进的遗传算法的性能达到了其最佳极限。改进的遗传算法识别精度并不会随着变异率的增大而减小，说明大变异不会破坏其遗传模式。

3) 噪声会对改进的遗传算法的精度产生影响，噪声强度越大，整体精度越低；当噪声强度不超过10%时，该遗传算法仍然能获得令人满意的结果。

4) 基于支承松动转子实验台的实测信号，利用改进遗传算法进行了参数识别。通过对比将识别结果代入系统的运动方程中所获得的仿真信号与基于松动故障实验台的实测信号，发现这两组信号的振动幅值相仿，频谱中频率成分相似，验证了识别结果的可靠性。

参 考 文 献

[1] Muszynska A, Goldman P. Chaotic responses of unbalanced rotor/bearing/stator systems with looseness or rubs [J]. Chaos Solitons & Fractals, 1995, 5(9):1683-1704.

[2] Ma Hui. Analysis of dynamic characteristics for a rotor system with pedestal looseness [J]. Shock & Vibration, 2011, 18(1-2):13-27.

[3] 马辉, 李焕军, 刘杨,等. 转子系统耦合故障研究进展与展望 [J]. 振动与冲击, 2012, 31(17): 1-11.

Ma Hui, Li Huanjun, Li Yang, et al. Review and prospect for research of coupling faults in rotor systems [J]. Journal of Vibration and Shock, 2012, 31(17): 1-11. (in Chinese)

[4] 王海飞, 陈果, 廖仲坤,等. 含支承松动故障的弹用涡扇发动机整机振动建模与机匣响应特征 [J]. 航空动力学报, 2015, 30(3): 627-638.

Wang Haifei, Chen Guo, Liao Zhongkun, et al. Modeling for whole missile turbofan engine vibration with support looseness fault and characteristics of casing response [J]. Journal of Aerospace Power, 2015, 30(3):627-638. (in Chinese)

[5] 王海飞, 陈果, 廖仲坤,等. 含支承松动故障的航空发动机非同步响应特征[J]. 振动、测试与诊断, 2016，36(5): 858-864.

Wang Haifei, Chen Guo, Liao Zhongkun, et al. Asynchronous response characteristics of aero-engine with bearing looseness fault [J]. Journal of Vibration, Measurement & Diagnosis, 2016，36(5): 858-864. (in Chinese)

[6] Sekhar A. Crack identification in a rotor system: a model-based approach [J]. Journal of Sound & Vibration, 2004, 270(4-5):887-902.

[7] 周进, 张伟, 杨晓楠. 基于大爆炸优化算法的结构参数识别 [J]. 江西科学, 2010, 28(2): 135-140.

Zhou Jin, Zhang Wei, Yang Xiaonan. Structural parameter estimation based on big bang-big crunch algorithm [J]. Jiangxi Science, 2010, 28(2): 135-140. (in Chinese)

[8] 榎本裕里, 杨晓楠. 粒子群优化算法在结构参数识别中的应用 [J]. 结构工程师, 2010, 26(3): 78-81.

Jiaben Yuli, Yang Xiaonan. Application of a particle swarm optimization algorithm in structural parameter identification [J]. Structural Engineers, 2010, 26(3): 78-81. (in Chinese)

[9] 韩放, 郭杏林, 高海洋. 基于改进智能算法的非线性转子系统的参数辨识 [J]. 振动与冲击, 2012, 31(17): 111-115.

Han Fang, Guo Xinglin, Gao Haiyang. Parameter identification of a nonlinear rotor system based on hybrid intelligent algorithm [J]. Journal of Vibration and Shock, 2012, 31(17): 111-115. (in Chinese)

[10] 李立新, 艾延廷, 王志，等. 基于遗传算法的多级盘转子平衡方案优化设计 [J]. 振动、测试与诊断, 2008，28(2): 139-142.

Li Lixin， Ai Yanting， Wang Zhi, et al. Optimum design for balance in multi-disk rotor installation based on genetic algorithm [J]. Journal of Vibration, Measurement & Diagnosis, 2008，28(2): 139-142. (in Chinese)

[11] 王兴贵, 王言徐, 智勇. 遗传算法在发电机励磁系统参数辨识中的应用 [J]. 电力系统及其自动化学报, 2010, 22(1): 76-79.

Wang Xinggui, Wang Yanxu, Zhi Yong. Application of genetic algorithm in generator excitation system parameters identification [J]. Proceedings of the Chinese Society of Universities, 2010, 22(1):76-79. (in Chinese)

[12] Ma Hui, Huang Jing, Zhang Suyan, et al. Nonlinear vibration characteristics of a rotor system with pedestal looseness fault under different loading conditions [J]. Journal of Vibroengineering, 2013, 15(1):406-418.

[13] 刘献栋, 何田, 李其汉. 支承松动转子系统模型及其故障诊断方法研究[J]. 振动工程学报, 2004, 17(S1):356-358..

Liu Xiandong, He Tian, Li Qihan. Research on dynamic model of rotor system with support looseness and its diagnosis method [J]. Journal of Vibration Engineering, 2004, 17(S1):356-358. (in Chinese)

[14] 成玫, 孟光. 含Alford力的非线性转子-滚动轴承系统动力分析 [J]. 中国机械工程, 2011(23): 2806-2812.

Cheng Mei, Meng Guang. Dynamic analysis of a rotor-ball bearing nonlinear system with Alford force [J]. China Mechanical Engineering, 2011, 22(23): 2806-2812. (in Chinese)

[15] 曹树谦, 王俊, 韩研研,等. 耦合故障转子系统的降维及动力学特性 [J]. 天津大学学报:自然科学与工程技术版, 2015(4): 318-327.

Cao Shuqian, Wang Jun, Han Yanyan, et al. Dimension reductions and dynamic characteristics of rotor system with coupling faults [J]. Journal of Tianjin University:Science and Technology, 2015(4):318-327. (in Chinese)

[16] 周明. 遗传算法原理及应用[M]. 北京：国防工业出版社, 1999:32-64.

[17] 史峰. Matlab神经网络30个案例分析[M]. 北京：北京航空航天大学出版社, 2010: 33-38.