利用自悬链模型研究系泊系统的设计问题
2018-07-16王希春曲贵江
◎王希春 王 静 曲贵江
(吉化第一高级中学校,吉林 吉林 132022)
近浅海观测网的传输节点由浮标系统、系泊系统和水声通信系统组成.本文将传输节点的浮标系统简化为底面直径2 m、高2 m的圆柱体,浮标的质量为1 000 kg.系泊系统由钢管、钢桶、重物球、电焊锚链和特制的抗拖移锚组成.锚的质量为600 kg,锚链为无挡普通链环,近浅海观测网的常用型号及其参数已给出.钢管共4节,每节长度1 m,直径为50 mm,每节钢管的质量为10 kg.注意锚链末端与锚的链接处的切线方向与海床的夹角不能超过16度.水声通信系统安装在一个长1 m、外径30 cm的密封圆柱形钢桶内,设备和钢桶总质量为100 kg,以下将100 kg记为钢桶的质量.钢桶上接第1节钢管,下接电焊锚链.尽量使水声通信系统工作效果最佳,要求钢桶尽量处于竖直状态.钢桶与竖直线的夹角超过5度时,认为设备不能工作.为了控制钢桶的倾斜角度,钢桶与锚链链接处悬挂一重物球.近海风荷载可通过近似公式F=0.625×SV2(N2)计算,其中S为物体在风向法平面的投影面积(m2),v为风速(m/s).近海水流力可通过近似公式F=374×SV2(N2)计算,其中S为物体在水流速度法平面的投影面积(m2),v为水流速度(m/s).
一、模型假设
1.假设浮标系统简化为规则的圆柱体后,浮标所受的浮力与简化前所受浮力的误差可以忽略.
2.假设锚、锚链、钢桶、钢管等在水中受海水的腐蚀作用不影响其自身的重力或浮力等受力,即题目提供的数据具有完全意义上的参考性.
3.假设钢桶底部与锚链末端切线的夹角近似为钢桶的倾斜角(近似为对顶角).
二、模型的建立与求解
此时整个系统只受风速为12 m/s的风的作用,系泊系统对浮标一定有一个系留作用,所以浮标最后一定处于一个稳定(平衡)状态.
首先把锚链和钢桶作为一个整体(记为系统A)进行受力分析(见图1),然后把锚链、钢桶和第一节钢管作为一个整体(记为系统B)进行受力分析(见图2),然后依次把锚链、钢桶和第一二节钢管看作一个整体(记为系统C),把锚链、钢桶和第一二三节钢管看作一个整体(记为系统D),把锚链、钢桶和四节钢管看作一个整体(记为系统E),进行受力分析.由于四节钢管的参数均一致,把与钢桶相连接的第一节钢管与海床夹角记为α2,依次类推,其余钢管与海床的夹角分别记为α3,α4,α5.系统C,D,E的受力分析图见系统B受力分析图.
锚链、钢桶作为一个整体(系统A)时的受力分析:
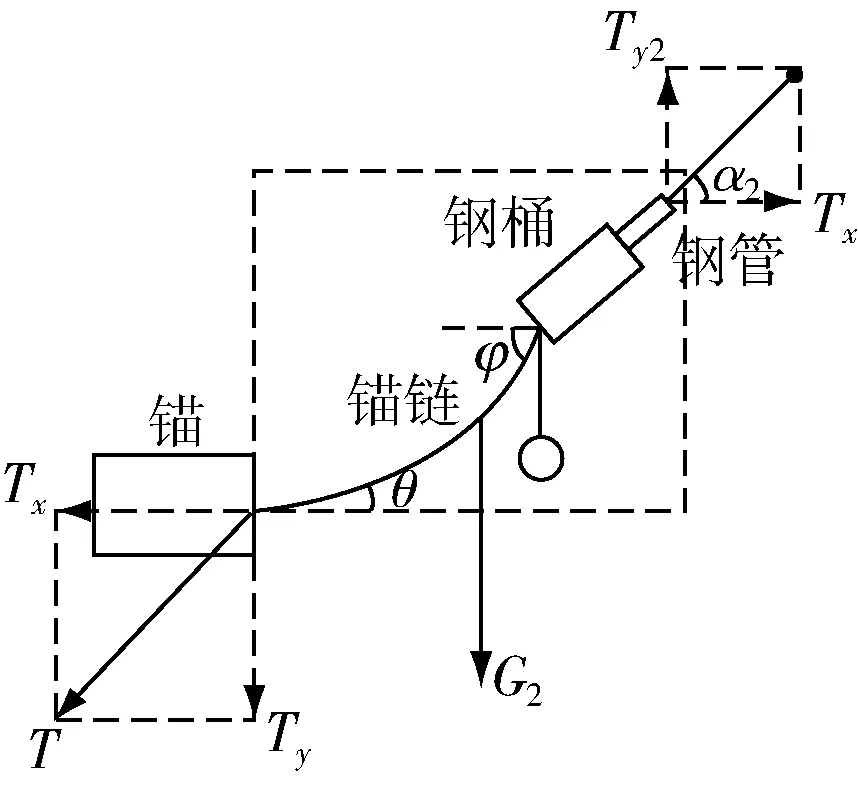
图2 系统B的受力分析
T:锚对锚链的拉力;Tx,Ty:T的水平分力与竖直分力;θ:锚链与海床夹角;G1:锚链的静重力;T1:钢桶、锚链、重物体所受拉力;Ty1,Tx:T1的水平分力与竖直分力;α1:钢桶与海床的夹角;φ:锚链顶部切线与水平方向夹角;
此时将锚链顶部与钢桶接触点处切线方向与水平方向的夹角近似认为和钢桶与海床的夹角α1相等.
系统B的受力分析图2,此图同样适用于对系统C,D,E的受力分析.
T:锚对锚链的拉力;Tx,Ty:T的水平分力与竖直分力;θ:锚链与海床夹角;φ:锚链顶部切线与水平方向夹角;α2:第一节钢管与海床的夹角.
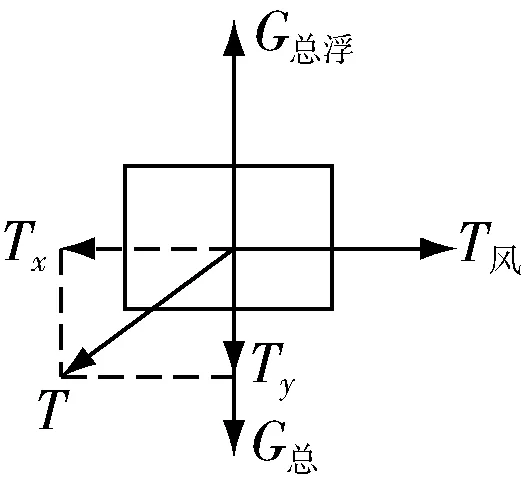
图3 除锚外的系统分析
对以上五个系统在竖直方向上分解力,得到五个受力平衡方程(公式(1)前五个).接下来对除锚以外整个系统进行受力分析(见图3),建立竖直方向和水平方向的受力平衡方程,即公式(1)方程组的最后两个.
G总浮:除锚以外的系统的总浮力;T风:风产生的风力;G总:除锚以外的系统的总重力.
将上述A,B,C,D,E五个系统竖直方向上的平衡方向与锚以外整个系统在竖直与水平方向上的平衡方程整理得到公式(1):
(1)
结合以上公式(1),钢桶的力矩平衡示意图如图4所示.
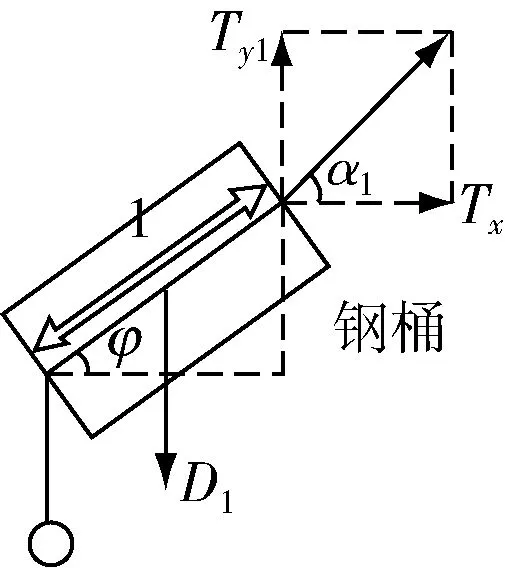
图4

图5
四节钢管的力矩平衡示意图均可用图5表示.
力臂为转动轴到力的作用线的距离支点到力的作用线的垂直距离l×sinαn.所以整理得到钢桶和钢管的力矩平衡公式(2):
(2)
根据数学中的三角关系式.得出一节钢管的高度可以表示为钢管的长度乘与海床倾斜角度的正弦值.钢桶的高度同样可以表示为钢桶的长度乘海床夹角的正弦值,其中钢管和钢桶的长度均为1 m.假设锚链的高度为h1,则可以将水深表示为:
h+sinα1+sinα2+sinα3+sinα4+sinα5+h1=18.
(3)
用Matlab编程可以解得吃水深度h=0.739 8 m以及钢桶与海床的倾斜角度α1=57.230 0°,四节钢管与海床的倾斜角度分别为α2=57.233 8°,α3=57.235 5°,α4=57.237 1°,α5=57.238 8°.
三、模型的评价与改进
1.可以考虑当更合理的一种状态即浮漂处于倾斜状态时对应的钢桶、钢管、锚链、浮漂的倾斜角度;
2.设计时间复杂度更小的算法,减小计算的时间.
