“让学引思”:初中数学课堂的新视点
2018-07-16陈忠山
◎陈忠山
(福建省龙海第一中学,福建 龙海 363199)
“让学引思”的教学模式在其本质上是属于让学生处于教学主体地位、提升学生对学习的兴趣与促进学生综合能力发展的尝试,这对于教师推进数学教学的深入和学生的自身的理解能力等方面都起到了很大的效果.动力是学习的源泉,只有先对所要学习的内容产生了一定的兴趣,学生才能发挥自己的能动性,更加有积极性地去掌握知识、了解方法.为了使这个问题得到充分的解决,本人不断地探索和实践,综合自己的一点心得和其他教师的看法,提出了以下几种行之有效的方法.
一、让学——充分发挥学生的主体能动性
“让学”是德国教育哲学家Martin Heidegger提出的教学理念,揭示了教学方法的本质及核心.“让”是一种让教师从课堂的主导者演变为课堂的引导者,使学生成为课堂上的主体,然后教师再以雅化语言以及整体的民主氛围,将学生被动接受知识转变为学生主体能动地参与教学.教师首先寻找知识点的着眼点,让学生们踊跃发言、各抒己见,使之充实、丰富,从而扩大成线、成面,最后教师再加以点拨、指导,整个课堂俨然成为一个动态的、生长性的稳固系统.
在数学教学中教师不仅要把抽象的问题具体化,给出一个学生便于理解的问题情境,来以此引起学生的兴趣,主动地参与到教学活动中并思考问题的答案.
例如,在讲等腰三角形的判定定理的时候,为了要引出等腰三角形的判定定理,通常提出问题:如图1所示,△ABC用什么方法可以判断它是一个等腰三角形呢?
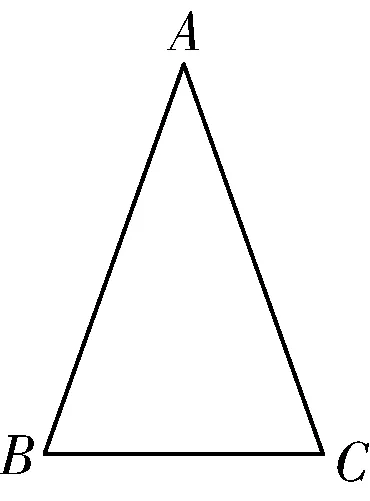
图1
图2
虽然直接明了地说出了问题,但是在学生看来可能就是一头雾水.所以,同样的是让学生明白什么是等腰三角形的判定定理,如果教师能先找出等腰三角形性质定理与等腰三角形的判定定理的内在联系,让学生明白定理的性质后,再提出下面这一个实际的问题:如图2所示,CA=CB,△ABC是等腰三角形,图因为滴了一滴颜料被遮住了,仅能看到一个底角∠A和底边AB,能不能再把原来的△ABC重新画出来呢?这下就点燃了学生们学习的热情,从学生们的回答来看也得到了不错的效果,有学生先用量角器度量∠A度数,再以AB为边作∠A=∠B;也有的学生取AB的中点E,再过点E作∠C的平分线等.通过这个例子我们可以知道,在教学一个定理的时候,如果它的概念性比较强且难以理解的时候,教师就应该努力给出一个合理的问题情境,使学生从实际中认识到所学知识的具体意义,引起了学生想要了解的兴趣,自然而然地就会主动去思考这个问题,再在教师给予的指导下,告诉学生们如何自主地去探索解决问题的方法,在实践中培养学生的创造能力.
二、引思——充分发挥学生的思考能性
不仅要让学生拥有主动学习的地位,还要激发出学习的欲望,让过去“填鸭式”教学成为历史.“引思”的方法在于教师对学生进行指引、启示、点亮,使得他们的思维方式、学习习惯、价值形成得到培养,只有引导学生对知识进行系统化的理解,点燃学生的学习热情,才能提高学生的知识素养和动手能力.
例如,向学生提问二元一次方程是什么?它的特征都有哪些?
学生:如果一个方程中含有两个未知数,且包含的未知数均为一次的,则这种形式的方程就称为二元一次方程.
教师:这名同学回答得真棒,根据二元一次方程的概念,那我们能不能来试着说出二元一次方程具备哪些特征呢?
教师:同学们先来判断一下下面哪些方程是二元一次方程吧!
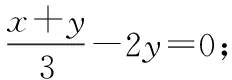
⑤y=2x+4;⑥ 2x+1=2-x;⑦ab+b=4.
设计意图:学生对二元一次方程已经有了一个初步的了解,为了让学生对“含有未知数的项的次数”的内在有进一步了解,先从教材上二元一次方程的概念入手,让学生对自己的理解有了矛盾,引发出学生去思考什么是“项的次数”,从而把学生对二元一次方程理解进一步加深了,让学生举例子也是一个必不可少的环节,这样才能把什么是“项的次数”这个概念给形象化.
通过引导学生自主取值,大胆地猜测x和y的值,再主动验证其正确性.让学生们可以知道二元一次方程的解就是:一对未知数的值能够使二元一次方程的左右两边相等.再引导学生看教材,加深对这个概念的印象,让学生来总结并体会“一对未知数的取值”的真正含义.
三、结 语
“让”与“引”的关系是辩证统一的,相互促进,相互影响,以“让”带“引”,再以“引”带学,从而让学生点线面结合,对所学习的知识有个系统的框架.当然,“让学引思”不是一个空洞的口号,这个目标实现需要每位教师们认真地研究,并且不断地反复实践,再反思自己的教学成果,从而在实践中得到“让学”的方法,提炼出自己特有的“引思”技巧.这样才能使得学生真正地达到乐学、善学,取得事半功倍的效果.
