波流耦合作用下双层砂质海床累积液化特征数值分析❋

2018-10-15刘小丽崔浩男

中国海洋大学学报（自然科学版） 2018年11期

刘小丽，周杰，崔浩男，何影

(1. 中国海洋大学环境科学与工程学院，山东青岛 266100； 2. 山东省海洋环境地质工程重点实验室，山东青岛 266100)

波流共同作用下海床发生的失稳破坏，对海洋构筑物地基稳定性构成威胁。1970年代以来，基于Biot固结理论，较多学者通过解析、试验和数值模拟[1-4]等方法对波浪作用下海床响应及其稳定性进行了研究。Sassa和Sekiguchi[5]对细砂海床的波浪响应进行了离心模型试验研究，结果表明较大的波浪荷载可以导致细砂海床内孔隙水压力的累积，使海床发生渐进液化破坏。此外，Sassa等[6]对风暴浪作用下的细砂质海床动力响应进行了现场监测，发现当波高大于2 m时海床内的孔隙水压力会发生累积。上述研究表明，一定条件下波浪荷载会导致砂质海床内的孔压累积，并可能发生液化。但这些分析中主要考虑了波浪作用，忽视了海流的影响。

Ye和Jeng[7]基于u-p模型研究了波流和海床参数对单层海床瞬态响应及液化的影响。Liu等[8]基于u-p理论，推导了波流共同作用下海床瞬态动力响应的解析解，分析了流速对海床瞬态响应和液化的影响。Zhang等[9]提出了波流耦合作用下多孔介质单层海床响应的拟静力解析解。崔嵩等[10]分析了波流耦合作用下单层砂质海床瞬态与残余孔压的响应规律以及海床液化深度的变化规律。对于波流耦合作用下的双层海床，目前Wen和Wang[11]对其瞬态响应进行了数值计算，分析了波流和海床参数对双层海床液化及剪切破坏特征的影响，但由于海床的瞬态液化深度一般较小，难以全面反映双层海床的液化特征，因而有必要对其累积液化进行分析。

本文以双层砂质海床为研究对象，基于Comsol Multiphysics多物理场耦合有限元分析平台，对波流耦合作用下双层海床的累积液化特征进行数值模拟研究，重点分析不同渗透系数组合下海流流速与上下层海床相对厚度的影响。

1 数值计算模型及验证

1.1 波流荷载的计算

假设海水是不可压缩的非粘性流体，是无旋的，且深度是有限深的，Hsu等[12]给出了前进波与均匀流共同作用下海床表面的波流荷载解析解：

(1)

波浪-流圆频率满足下式：

(2)

ω=(λH)2ω2+ω0。

式中：ω、ω0、ω2分别为总圆频率、第1阶圆频率和第3阶圆频率(其中第2阶圆频率ω1=0)；d为水深；H为波高；λ为波数；U0为流速，当流的流动方向与波的传播方向一致时，为顺流(U0>0)；反之为逆流(U0<0)；g为重力加速度；ρw为海水密度。

根据公式(1)，可以计算波流荷载作用下海床表面波压力数值，用于波流耦合作用下双层海床瞬态响应计算中海床表面边界条件的施加。由于双层海床累积孔压计算时，需要利用波流作用下双层海床瞬态响应计算得到的循环剪应力幅值τmax(见下述)，故首先需要对海床的瞬态响应进行计算。关于波流耦合作用下双层海床的瞬态响应模型及计算，可参见文献[11]，由于本文侧重于分析双层海床的累积响应，故此处不再对其展开论述。

1.2 波流耦合作用下双层海床累积孔压计算模型

双层海床几何计算模型如图1所示，波长为L，水深为d，流速为U0，海床厚度为h，上层海床厚度为h1，下层海床厚度为h2。沿海床表面设为x轴，垂直于海床表面向上为z轴。假设海床土体为多孔弹性介质，各层海床中土体为均匀各向同性的饱和土体。

图1 双层海床几何模型Fig.1 The geometric model of two-layered seabed

海床累积孔隙水压力发展的控制方程可以表示为[13]：

(3)

式中：pr为累积孔隙水压力；Cv为土体固结系数。

式中：G为土体剪切模量；K为土体渗透系数；μ为土体的泊松比；γw为海水重度；孔压累积源项f(x，z，t)为[14]：

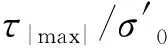
式中：γ′为土体容重；K0为土体侧压力系数，可通过K0=μ/(1-μ)求得；α、β为控制孔压增长速率的参数，是与土体相对密度Dr相关的经验系数。

海床累积孔压计算的初始条件和边界条件为：

pr(x，z，0)=pr(x，0，t)=0，

在海床两侧边界处，采用周期性边界条件，即：

pr左=pr右。

上下层海床间的连续边界条件：

pr上=pr下。

利用上述累积孔隙水压力计算的数学模型，基于Comsol Multiphysics多物理场有限元分析平台，可以对波流耦合作用下双层海床的累积孔隙水压力进行数值计算分析，并进一步探讨其累积液化特征。

1.3 计算模型验证

为验证计算模型的适用性，将波浪作用下海床累积孔压的试验值与数值计算结果进行对比。试验数据与相应计算参数均来自文献[3]，具体的计算参数见表1，对比结果如图2所示。

表1 波浪与海床参数Table 1 Parameters of wave and seabed

图2(a)和(b)分别为累积孔隙水压力随时间与深度的发展变化曲线，为了与文献[3]中的孔压坐标表示一致，便于数据的对比分析，图中累积孔隙水压力用相对坐标即累积孔隙水压力Pr与海水重度rw的比值表示，单位cm。

从图2中可知，本文数值计算结果与文献[3]中试验测试的结果基本一致，表明了数值计算结果的可靠性。根据文献[3]中的分析可知，该数值计算模型目前只适用于模拟累积孔隙水压力的上升阶段，由于本文侧重于分析累积孔隙水压力上升导致海床液化特征的分析，因此，采用该数值计算模型进行计算分析。

图2 累积孔隙水压力试验值与计算值的对比Fig.2 Comparison of the experimental data and the present model results for residual pore water pressure

2 算例分析与讨论

2.1 计算参数与累积液化判别准则

以双层砂质海床为研究对象，分析波浪-流共同作用下的累积液化特征，具体的计算参数如表2中所示。根据相关文献可知[15-16]，砂质土的渗透系数可从10-2～10-6m/s，本文分析中渗透系数最小值取到10-6m/s量级，用于分析透水性相对较差时双层海床累积液化特征。

表2 波流作用下双层海床计算参数Table 2 Calculation parameters of the two-layered seabed under wave and current interaction

海床的瞬态孔压和累积孔压一般是同时存在的，因此对海床累积液化的判别中，应考虑二者的共同作用。在瞬态液化判别准则的基础上[17]，考虑累积孔压的影响，得到海床累积液化判别准则为(式中正应力以拉为正)：

-γ′z+(Pb-posc-pr)≤0。

(4)

式中posc为海床瞬态孔隙水压力。

2.2双层海床累积液化特征分析

2.2.1海流流速的影响考虑到波流荷载的影响深度相对较小，上层海床厚度取为0.1h(即海床总厚度的0.1倍)。此处以上下层海床渗透系数分别为10-5与10-4m/s组合为例，分析不同流速影响下双层海床累积液化特征。

如图3所示分别为k1k2时,不同流速下海床累积孔压随深度的分布图。可以看出，逆流使海床累积孔压减小，顺流使其增大，且顺流对累积孔压的影响程度更大。究其原因在于，与无流相比，顺流会导致波流耦合作用下海床表面波压力增大，从而导致孔隙水压力增大；反之，逆流会导致海床表面的波压力减小，从而导致孔隙水压力减小[7]。从图3(a)可知，当k1k2时，累积孔压的峰值出现在渗透系数较小的下层海床中，基本位于0.2h深度处。

图4所示为不同流速下海床累积液化区分布图，顺流流速使海床液化区范围增大，增大了海床的不稳定性；逆流流速使海床液化区范围减小，有利于海床稳定。流速对液化区的影响规律与其对累积孔压的影响规律相一致，根据累积液化判别准则式(3)可知，累积孔压越大，海床越容易发生液化，因而其液化范围越大。从图4(a)中可知，当流速为-2 m/s 时，液化区只分布在波谷处，最大液化深度约为0.8 m；当流速为2 m/s时，液化区在整个波长范围内分布，只是由于瞬态孔压的影响，波峰处液化深度最小，波谷处液化深度最大，可达3.8 m，是无流时海床液化深度的2.7倍。因此当考虑海床的累积液化效应时，实际海况中较大流速的影响不容忽视。

图3 不同流速下海床累积孔压随深度的分布图(t= 100 T)Fig.3 The vertical distribution of residual pore pressure with different currents(t=100 T)

图4 不同流速下海床累积液化区分布图(t= 100 T)Fig.4 The distribution of residual liquefaction zone with different currents(t= 100 T)

图4(a)与(b)对比可知，k1k2时的液化区，说明在渗透系数较大的海床上覆盖一层渗透系数较小的土层，会增大海床的液化区，反之，则会减小海床的液化区。

2.2.2上下层海床相对厚度的影响针对双层砂质海床不同的渗透系数组合，分析上下层海床相对厚度对海床累积液化特征的影响，海流流速取为 2 m/s。

(1)上层海床渗透系数k1大于下层海床渗透系数k2

上层海床的渗透系数k1大于下层海床渗透系数k2时，双层砂质海床上下层相对厚度不同时的液化区分布如图5所示，其中图5(a)～(c)分别对应不同的渗透系数组合。

从图5(a)可知，对于渗透系数为10-5m/s的单层海床，其最大液化深度为2.9 m，随着渗透系数为10-4m/s的上层海床厚度h1的增加，双层海床的最大液化深度逐渐降低，当上覆海床厚度增加至2 m时，其最大液化深度降低至最小，为0.9 m，与渗透系数为10-4m/s的单层海床相同。图5(b)上下层海床相对厚度对液化分布特征的影响规律与图5(a)相似，只是上层海床的厚度h1达到3 m时，其最大液化深度降低至最小，与渗透系数为10-4m/s的单层海床相同，其主要原因是相对于图5(a)，图5(b)下层海床渗透系数较小10-6(m/s)，使孔压更易于累积，导致下层海床的影响相对增强。图5(c)中的上下层海床渗透系数均相对较小，故虽然上层海床渗透系数比下层海床渗透系数大1个数量级，但从海床累积液化的最大深度来看，上下层海床相对厚度的影响较小，如对应上层海床厚度从0～35 m，其最大累积液化深度为2.9～3.2 m，其变化较小。

从上述分析中可知，对于双层砂质海床，当k1>k2时，即在渗透系数较小的海床上覆盖一层渗透系数相对较大的土层，相对于渗透系数较小的单层海床，其累积液化深度会降低，但其具体效果应视实际海床计算参数而定。此处的算例中，当上覆海床渗透系数为10-4m/s时，对降低海床累积液化深度的效果显著，其降低幅度与上覆海床的厚度及下层海床的渗透系数有关，下层海床渗透系数越小，则需上覆海床厚度越大，其效果才越明显。一般上覆海床厚度达2 m时其效果已较好；当上覆海床渗透系数为10-5m/s时，由于其渗透系数已经相对较小，双层海床累积液化深度的降低效果并不明显。

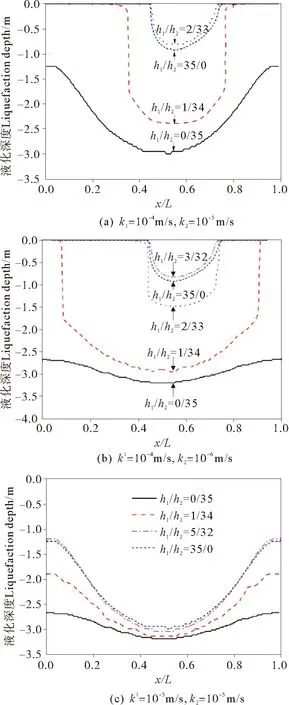
图5 不同h1/h2时海床累积液化区分布图(t= 20 T)Fig.5 The distribution of residual liquefaction zone with different h1/h2(t=20 T)

(2)上层海床渗透系数k1小于下层海床渗透系数k2

上层海床渗透系数k1小于下层海床渗透系数k2时，不同上下层海床厚度条件下的累积液化区分布如图6所示，图6(a)～(c)分别对应砂质海床不同的渗透系数组合。

图6(a)中显示，对于渗透系数组合为k1=10-5m/s，k2=10-4m/s的双层海床，当上层海床厚度h1为1 m时，相对于渗透系数k2为的单层海床最大液化深度0.9 m，此时双层海床的最大液化深度迅速增加至2.4 m。此后，随着上层海床厚度h1的继续增加，双层海床的累积液化深度逐渐增加，当h1增加至6 m时，双层海床的累积液化深度增加至最大，其值与渗透系数为k1的单层海床一致。表明在渗透系数较大的海床上覆盖一层渗透系数较小的海床，会导致其累积液化深度明显增加，因为渗透系数较小的土层会使海床的孔压更易累积，不易消散。在此渗透系数组合下，双层海床的最大累积液化深度与渗透系数为k1的单层海床相同。

对于图6(b)与6(c)所示的上下层海床渗透系数组合，从图中可以看出，当上层海床厚度h1为1 m时，双层海床液化深度最大，此后随着上层海床厚度的增加，海床液化深度迅速降低。当h1增至4 m时，双层海床液化深度与渗透系数k1为的单层海床一致。这种现象表明，当上层海床的渗透系数降低至10-6m/s，而下层海床的渗透系数相对较大时，对应上层海床的某一厚度(此处为1 m)，该双层海床的累积液化深度会显著增加，且其液化深度的数值大于渗透系数为10-6m/s的单层海床液化深度。出现该种现象的原因在于，上层海床的渗透系数k1降低到一定数值后(此处经计算为10-6m/s)，如果下层海床处于波流荷载的显著影响深度范围内，由于上层海床的弱透水性，则下层透水性相对较好的海床内的孔压会迅速累积而难以消散，即会导致双层海床在一定深度范围内出现较大的累积孔压，进而导致较大的累积液化深度，故对应于上层海床的某一厚度(此处为1 m)，双层海床的累积液化深度会达到一个最大值；之后随着上层海床厚度的增加，波流荷载对下层海床的影响逐渐减弱，导致下层海床中累积孔压的降低，因而海床液化深度随之减小，并最终达到与渗透系数为k1的单层海床相同的液化深度。故在图6(b～c)渗透系数的组合下，双层海床的最大累积液化深度可能会远大于渗透系数为k1的单层海床累积液化深度，具体取决于上下层海床的相对厚度。

上述分析表明，对于双层砂质海床，当k1