地方应用型本科院校高等数学教学改革研究——以函数的连续性为例

◎张府柱　杜　云　张文林

(六盘水师范学院，贵州　六盘水　553001)

地方新升本院校定位为应用型本科院校时，这类学校在教育教学上基本模仿研究型大学办学.在教学过程中产生了诸多问题，例如，随着实践学分的增加，给理论教学在学时分配上提出了挑战，以高等数学为例，升本前专科生每学期18周的上课时间，周学时达到6节，升本后的本科生每学期16周的理论授课时间，2周的实践教学，高等数学的周学时一般是4学时，从108节减少到64节，反映出来的情况是理论掌握不好，计算能力薄弱，应用能力较差，与应用型的定位不相匹配.所以，在教学方法上要进行相应的改变.下面将以函数的连续性教学为例，介绍一下我们的做法，以供同行参考交流.

用极限讨论函数的分析性质，连续性是第一个.

同济大学数学系编写的高等数学第七版教材，是通过自然界中的一些连续的现象，如气温的变化、河水的流动、植物的生长等给学生一些连续的映象，然后分析变量的增量引入点连续的概念，然后介绍右、左连续的概念，很多教材基本上以它为蓝本进行编写.而对地方新升本的应用型本科学生来说，还是不能适应，依然不知道连续性是什么？连续性有什么用处？

下面介绍一下我们的处理方式.

一、由观察几个函数图形，在学生的脑海中产生直观的函数在一点连续的映象

提问：根据你们对“连续”的理解，说说下面几条曲线的连续性.

学生都能说出图1、图2和图3的曲线都不连续，图4的曲线连续.其实学生对连续的直观映象是正确无误的.

图1　不连续

图2　左连续

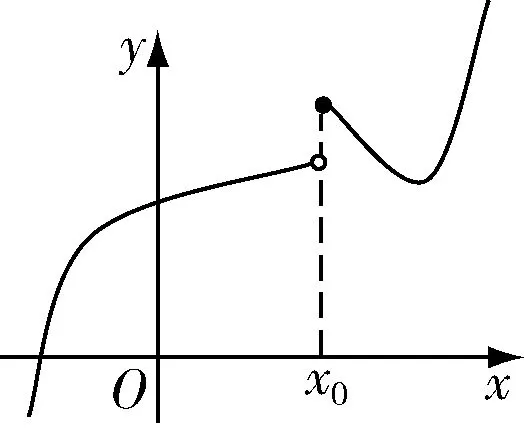
图3　右连续

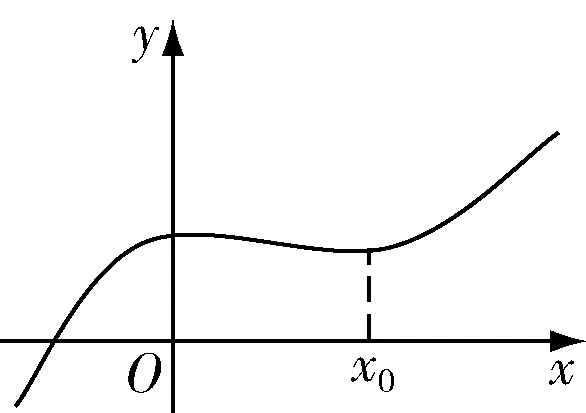
图4　连续

提问：前三条曲线不连续，它们之间有什么区别？

第一条曲线在x0是断开的，第二条曲线在x0处也是断开的，但是，点(x0，f(x0))和左边的曲线是连在一起的，教师引导学生这就是左连续.这时，学生就能正确地回答图3的曲线是右连续，图4是连续的.

从这一问一答中，学生基本上对函数的连续性有了正确的直观映象.

二、用语言来描述函数在一点的左连续、右连续和连续

先这样启发学生，设想一个人沿着曲线行走，不连续的曲线从左端能走到右端吗？左连续、右连续和连续情况如何？学生基本上能回答：不连续的曲线从左端不能走到右端；左连续的曲线可以从左边到达(x0，f(x0))点，右连续的曲线可以从右边到达(x0，f(x0))点，连续的曲线可以从左端走到右端.通过这样的设想，在启发学生回忆一下函数极限，函数的连续性就与极限过程联系起来，于是得到了下面的一些关系.

左连续⟺点(x0，f(x0))左边的图形连接起来⟺

右连续⟺点(x0，f(x0))把右边的图形连接起来⟺

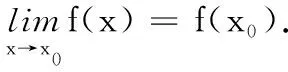
到了这里，函数的连续性已经在学生的脑海里基本建立起来了，而且三者之间的关系也被揭示出来了，连续⟺既左连续又右连续.上述直观定义还缺少严格性，我们需要附加一些条件才能得到严格的定义.

三、函数在一点的连续性

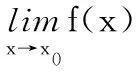
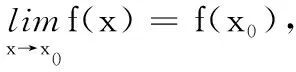
那么就称函数y=f(x)在点x0连续.

其本质就是极限值等于函数值，于是我们得到下面的等价定义.

定义1′函数y=f(x)在点x0连续⟺∀ε>0，∃δ>0，当|x-x0|<δ时，有|f(x)-f(x0)|<ε.

提醒学生注意这个定义与极限的ε-δ定义的区别与联系，并类比函数极限的几何意义写出函数连续性的几何意义.

若记Δx=x-x0，称为自变量x在点x0处的改变量(或增量)，函数对应的增量Δy=f(x0+Δx)-f(x0)，则有下面的等价定义.

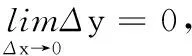
这个定义可以很好地解释动物和植物的生长是连续地变化着的，因为当自变量时间趋于无穷小时，因变量高度也趋于无穷小，所以我们看不到它们在往高处生长.

类似地，我们可以定义单侧连续以及单侧连续与连续的关系.

四、函数在一点的单侧连续性

设函数y=f(x)在点x0的某一邻域内有定义.

单侧连续性也同样具有连续类似的等价定义，可以由学生作为练习.

定理1连续⟺既左连续又右连续.

五、总　结

以上的教学过程，打破了传统的先给出一系列的定义，再举若干例子，最后到若干定理的教学过程.它首先通过观察图形，给学生连续与不连续的直观认识，通过教师不断启发，用自己的语言对函数的连续性进行描述，通过一个设想和前面学习的极限过程对比，得出了用极限来给连续性下定义.再由极限的变形得出函数连续性的其他形式的定义.从教学效果来看，学生对函数在一个点的连续性有了深刻的理解，对下一步学习函数的间断点的区间连续打下了坚实基础.

地方应用型本科院校的教学目标与研究型大学的教学目标不同，对于一个数学对象，前者需要掌握是什么?了解为什么?重点是怎么做(应用)?后者遵循一种不完全的公理化线索，不但要掌握是什么，而且通过严格的逻辑推导为什么，了解怎么办(应用).所以，根据不同的教学目标，选择不同的教学方法，这才是真正的因材施教.