基于黏流理论的半潜式平台近场干涉数值计算

， ，

(江苏科技大学， 江苏 镇江 212003)

0 引 言

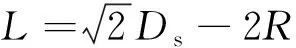
在国内，姜胜超等[8]针对波浪作用下的四柱结构近场干涉问题进行研究，应用势流理论对其现象与机理进行分析，揭示圆柱结构周围的波高变化对入射频率的依赖关系。张磊等[9]以深吃水多立柱平台为研究对象，基于绕射和辐射势流理论，对比分析不同浪向下绕射和辐射波面的变化规律和平台结构形式对波浪高程的影响，结果表明：由于平台为多立柱结构，使得绕射和辐射波发生强烈的近场干涉效应，局部波面放大。在特定海况条件下，绕射和辐射效应使得总波面高程增大。蒋安等[10-11]采用势流理论的方法对波浪作用下的半潜式平台周围近场干涉问题进行预报，结果表明：前后立柱的最大波面爬升并不发生于迎浪点和背浪点，而在其两侧，干涉现象发生时，并不是所有位置点都有很大的波面升高，而是在特定点产生局部极大值。单铁兵[12]在上海交通大学海洋工程国家重点实验室对一座半潜式平台模型进行一系列的试验研究，分析不同立柱间距波长比、入射波陡参数和波浪散射参数等对立柱之间水动力干扰的影响，重点考察前、后立柱周围的非线性水动力干扰对波面分布的影响，并探索了柱群发生近场干涉现象时波动场的分布特征，试图揭示该现象的作用机理。

本文采用计算流体力学软件FINE/Marine，结合自编程后处理软件开展半潜式平台近场干涉数值模拟计算，并对不同波浪要素(入射波高、周期、浪向角)以及3种平台模式对平台四立柱间近场干涉影响进行研究。

1 计算模型

1.1 计算模型和网格划分

采用SolidWorks软件完成半潜式平台三维建模，导入Hexpress软件进行网格划分。建立1个长415 m(约5L，L为平台长度)，宽230 m(约3L)，高90 m(约1L)的方形计算域，平台所处位置距入口处约3L，距两侧约L，距顶部约0.5L。对半潜式平台附件及自由液面进行局部加密处理。半潜式平台三维模型与平台表面网格划分如图1所示。半潜式平台的主要参数见表1。

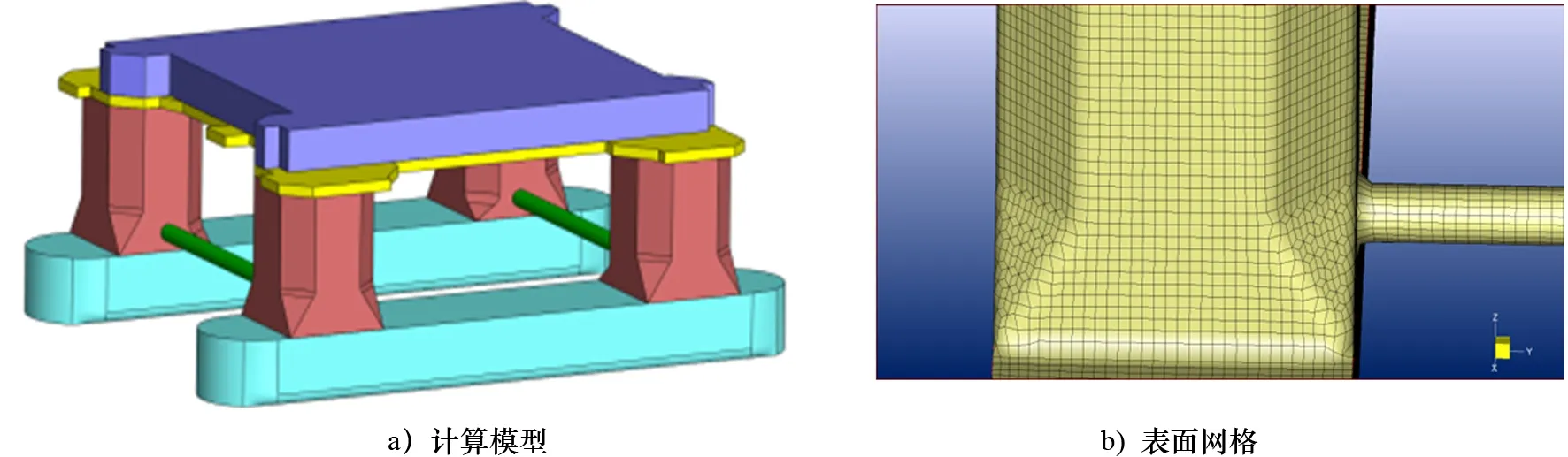
图1 计算模型与模型表面网格

表1 半潜式平台主要参数

1.2 半潜式平台计算工况和系泊系统

图2 悬链线的设定示意图

半潜式平台近场干涉问题包含入射波、反射波、辐射波的叠加，流场较为复杂，本文采用控制变量的方法研究半潜式平台近场干涉问题： (1)不考虑辐射波的平台固定模式。(2)半潜式平台垂向3个自由度约束强弱对近场干涉的影响，自由模式(约束弱)与系泊模式(约束强)。

规则波只存在1个主频，方便描述近场干涉在某一频率范围的发生机理。本文选取规则波工况，波高H取8 m、10 m，周期T取8 s、10 s，规则波环境条件选取见表2。

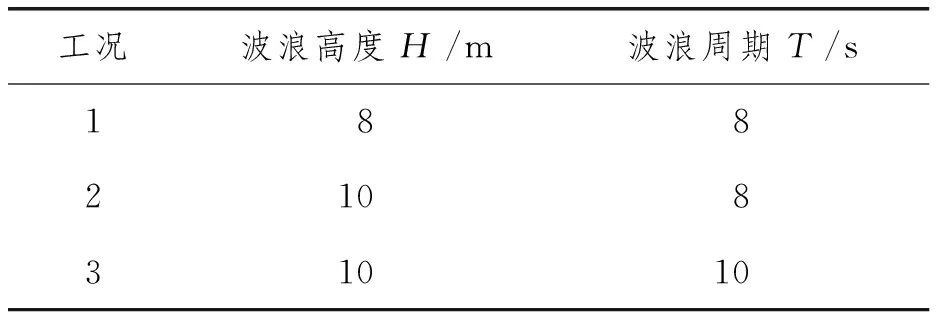
表2 规则波环境条件

系泊系统采用8根锚链线，每个立柱的拐角处分别布置2根。图2为系泊系统分析中使用的坐标系以及锚链线编号，半潜式平台悬链线的属性见表3。

表3 半潜式平台悬链线属性

1.3 近场干涉观测点选取

半潜式平台近场干涉主要发生在平台4根立柱所围成的内部区域，在4根立柱形成的范围内均匀地布置25个观测点，每2个观测点间隔约8 m。半潜式平台近场干涉观测点布置如图3所示，当浪向角β=0°时，沿波浪传播的方向(波向线)布置F、I、J、K、L 5组观测点，沿垂直波浪传播方向(波峰线)布置A、B、C、D、E 5组观测点。

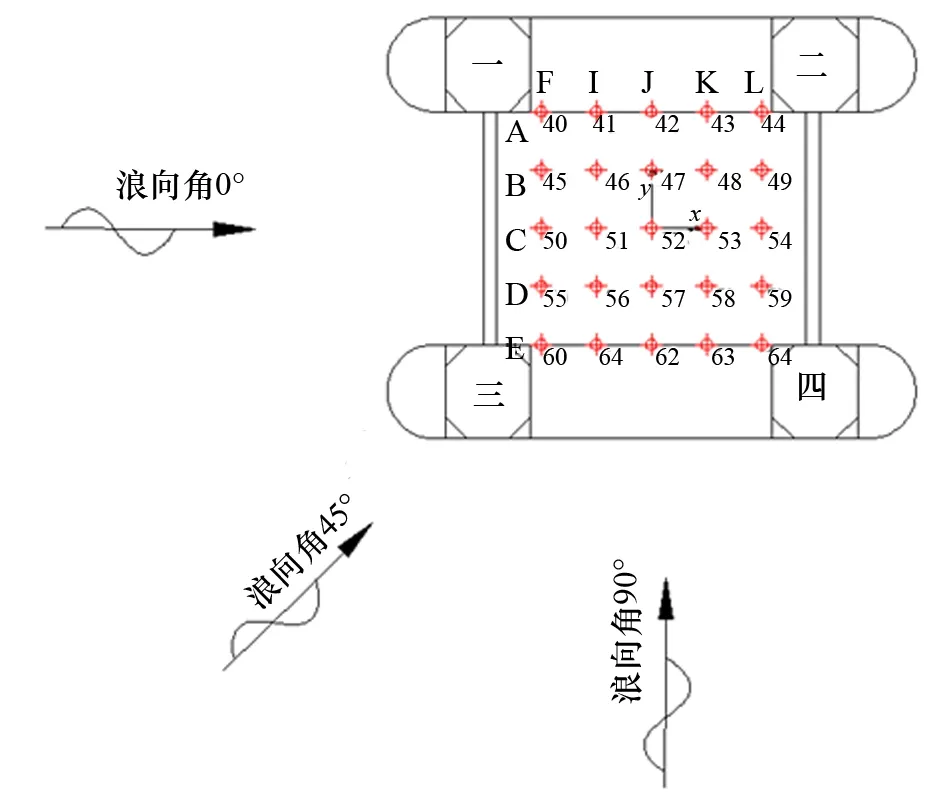
图3 半潜式平台近场干涉观测点布置

2 计算结果与分析

计算结果采用无量纲参数进行分析，定义Ai/(H/2)为无因次化的波面升高，即比波高，即无因次波浪爬升，其中Ai为波面升高幅度，H为入射波高。不规则波采用谱能(本文中“谱能”指波浪谱的势能，不计动能)进行分析，观测点谱能的大小等于观测点波面升高幅度的平方。

2.1 半潜式平台4根立柱内波浪演化规律

以半潜式平台固定模式下波浪入射角0°、H=10 m、T=8.0 s为例进行分析。图4为4立柱内场波浪沿入射波传播方向和垂直于入射波浪传播方向的分布规律，可以看出：波面升高沿波浪传播方向(波向线)呈现“W”趋势，垂直于波浪传播方向分布情况较为复杂，波峰线出现弯曲，由远场的二维波发生为三维波。出现这一现象的原因为：(1)入射波沿波浪传播方向经过一、三和二、四号立柱时，受到立柱的挤压作用，立柱内侧的波面抬升，因此2个端部的平均波高增量较大。(2)入射波的波长与平台主尺度相近，入射波与二号、四号立柱的反射波在4根立柱中心区域汇聚叠加，出现一个较大的波面抬升，形成“W型”的中间高点。(3)从“ROW F”曲线的特征可以看出：流体受到挤压，流速增加，其中中间点流速最大，流速大的地方压强较小，因此波峰线在中间点出现下凹。(4)从“ROW J”曲线可以看出入射波与反射波叠加最强的位置为4根立柱的几何中心点。

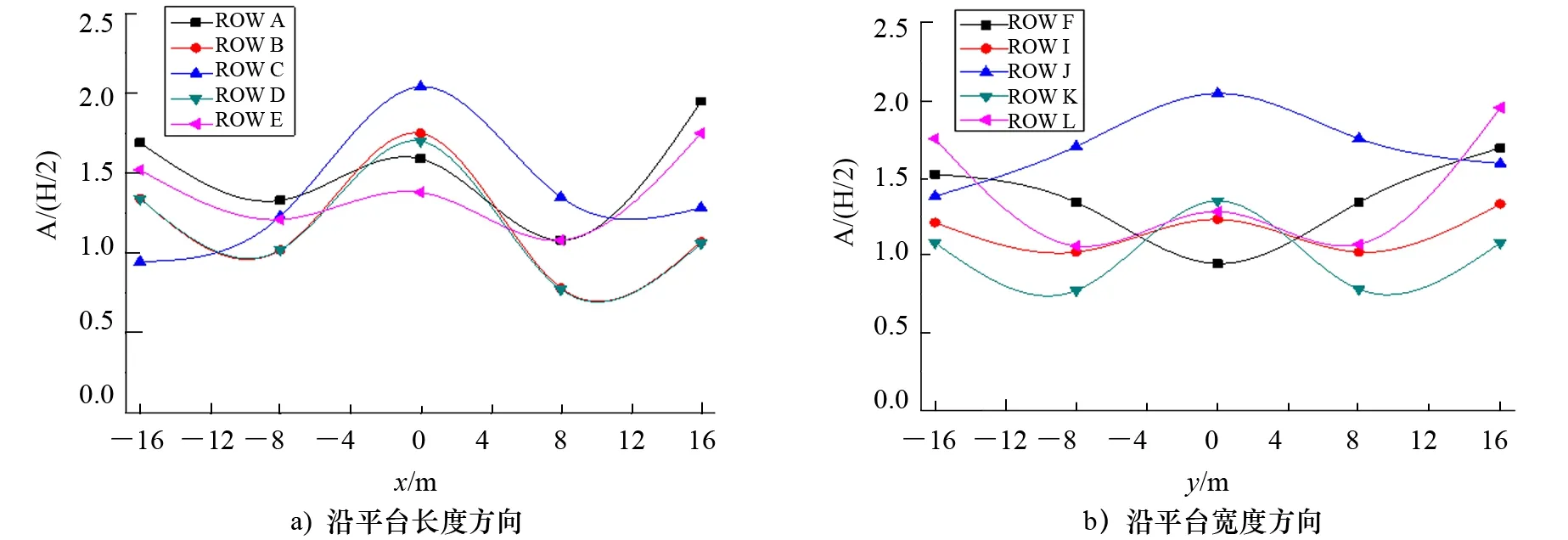
图4 波面升高沿平台长度和宽度方向变化曲线

2.2 半潜式平台四立柱间波面分布规律

图5为半潜式平台在固定模式下4根立柱间波面分布云图，分布云图代表的是观测点的波面升高极大值，并不是代表某一时刻平台内场的波面情况。从图5中可以看出：(1)浪向角对平台近场干涉效应有一定影响，浪向角β=0°和β=90°时，平台水下部分具有良好的对称性，平台内场波面关于波浪传播方向的中性轴呈对称分布。浪向角β=0°时，波面汇聚的峰值点位于4根立柱几何中心；浪向角β=90°时，波面汇聚的峰值点后移至后方两立柱的前缘中心位置；浪向角β=45°波面呈非对称分布，下浮体所处位置附近的波面升高普遍大于无下浮体的位置。由此可见，下浮体对流体的阻塞效应，直接影响4根立柱内场干涉。(2)浪向角β=0°和β=90°时，入射波浪爬升效应，在前立柱迎浪面附近波浪爬升较大。在前立柱后缘内侧波面升高值较小，由于流体绕过立柱在此出现分离现象，形成漩涡，波浪能量较低。平台中心对称轴处波面升高达到一个峰值(下浮体和4根立柱内缘的反射波与入射波在此交汇，交汇位置与入射波波浪周期有关)。后立柱前缘内侧波面升高较大，是由于入射波浪沿立柱表面爬升所致。由于前立柱的遮蔽效应，后立柱前的波浪升高小于前立柱迎浪面。后立柱后缘波面升高普遍较低，波浪传播过程中能量不断减小。(3)浪向角β=45°在平台中心对称轴处并没有出现峰值，而出现了低压区。这是由于迎浪面立柱和下浮体的阻塞效应较为严重，在立柱后缘形成涡流，出现低压区，波浪沿后立柱迎浪面爬升，在此出现较大的波面抬升。

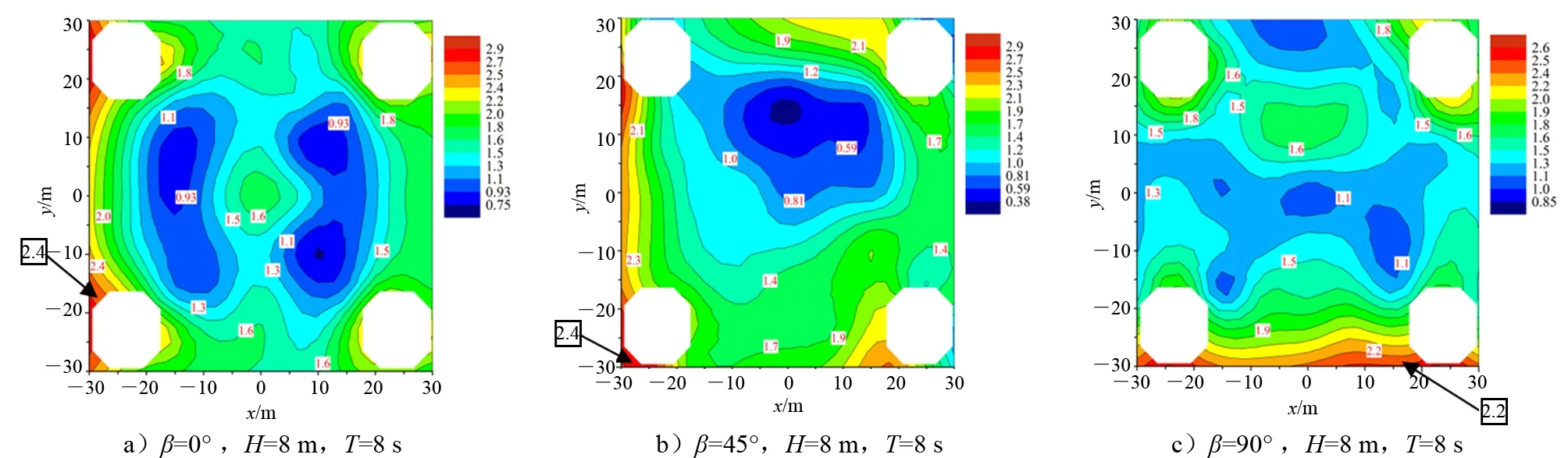
图5 平台固定模式下波面分布云图

2.3 不同约束模式对半潜式平台近场干涉的影响

以入射角0°、H=10 m、T=8.0 s为例，计算得3种约束模型下半潜式平台4根立柱间波面分布云图，如图6所示。表4为不同模式下最大波面升高及相应的观测点编号。从图6和表4中可以看出：相同入射波浪条件下，浪向角β=0°、β=90°时，波面升高最大值都出现在平台的中心位置处(观测点52号)；浪向角β=45°时，波面升高最大值出现在4号立柱内侧区域(观测点64号)；浪向角β=45°时，内场波面升高比其他浪向角大，近场干涉现象较为明显，最大波面升高可以达到入射波高的2.57倍。

图6 平台3种模式下波面分布云图

表4 平台3种模式下波面升高

入射波浪传播过程中不同时刻半潜式平台4根立柱结构和下浮体之间存在的水动力干扰不同，内场波面分布情况不同，所对应的平台4根立柱间近场干涉现象也不同。图7为某一时刻不同浪向角下半潜式平台4根立柱间内场波面分布云图，可以看出：入射波浪传播到4根立柱中部时，平台4根立柱结构和下浮体之间会存在明显近场干涉现象；出现近场干涉时，入射波波能不断向平台4根立柱的内侧聚集，而且入射波浪、遇立柱和下浮体产生的反射波浪与平台自身运动产生的辐射波浪在平台内场叠加较为频繁，波面分布极为复杂；不同浪向角对平台近场干涉效应的影响也不同，浪向角β为0°和90°时，平台内场波面分布规律相似，而浪向角β=45°时略有不同，这是由于入射波浪向前传播过程中受到下浮体和横撑阻碍较为严重。

图7 平台4根立柱间内场波面分布云图

3 结 论

(1) 平台4根根立柱间内场发生干涉后，波峰线出现弯曲，沿波浪传播方向出现峰谷值不对称的现象。

(2) 波浪入射角对平台近场干涉效应有一定影响，浪向角β=45°较浪向角β=0°和β=90°的近场干涉现象更为明显，波面升高极大值主要出现在平台中心位置附近和后立柱内侧区域。

(3) 周期较小时，入射波、反射波、绕射波与结构运动的辐射波叠加较为频繁，观测点最大波面升高较大；周期较大时，对近场干涉现象影响较小。

(4) 不同模式平台内场波面分布规律相似，近场干涉所引起波面升高所对应位置比较接近，但是系泊模式和自由模式比固定模式近场干涉引起的内场波面升高大。

(5) 近场干涉现象发生于4根立柱和下浮体间，自由液面波面升高并不是出现在内场区域所有的观测点，而是在平台内场局部出现波面升高极大值。

波浪近场干涉现象在半潜式平台周围的确存在，最大波面升高可以达到入射波高的2.57倍，较大的波面升高会引起平台结构受到波浪非线性砰击、飞溅以及甲板上浪现象的概率将会增加，导致平台甲板结构和机械设备的破坏从而威胁到平台的安全性能，所以半潜式平台的波浪近场干涉现象须予以关注。

[ 1 ] SIMON M.MultipleScattering in Arrays of Axisymmetric Wave-Energy Devies(Part 1): A Matrix Method Using A Plane-Wave Approximation[J]. J. Fluid Mech,1982, 120(120): 1-25.

[ 2 ] MANIAR H D, NEWMAN J N. Wave Diffraction by a Long Array of Cylinders[J]. J. Fluid Mech,1997, 339(339): 309-330.

[ 3 ] EVENS D V, PORTER R. Trapped Modes about Multiple Cylinders in a Channel [J]. J. Fluid Mech, 1997, 339(339): 331-356.

[ 4 ] EVANS D V, PORTER R. Trapping and Near-Trapping by Arrays of Cylinders in Waves[J]. Journal of Engineering Mathematics, 1999, 35(1-2): 149-179.

[ 5 ] PORTER R, EVENS D V. Rayleigh-Bloch Surface Waves along Periodic Gratings and Their Connection with Trapped Modes in Waveguides [J]. J. Fluid Mech, 1999, 386(386)：233-258.

[ 6 ] MALENICA S. Second Order Interaction of Water Waves with Arrays of Vertical Cylinders[C]// Proc 2nd Congress of Croatian Society of Mechanics, 1997.

[ 7 ] OHL C O G, TAYLOR R H, TAYLOR R E, et al.Water Wave Diffraction by a Cylinder Array (Part 2): Regular Waves[J]. J. Fluid Mech, 2001, 442(442): 33-66.

[ 8 ] 姜胜超 ,吕林, 滕斌, 等. 四柱结构在波浪作用下的近场干涉[J]. 哈尔滨工程大学学报, 2011,32 (05): 546-554.

[ 9 ] 张磊 ,李彬彬, 欧进萍.深吃水平台立柱周围的绕射和辐射波浪高程数值模拟[C]//第十一届全国水动力学学术会议, 2012.

[10] 蒋安 ,汪学锋, 李欣.波浪作用下半潜平台近场干涉问题的研究[J]. 中国海洋平台, 2013(06): 38-44.

[11] 蒋安.半潜式平台二阶气隙及近场干涉问题的研究[D]. 上海: 上海交通大学, 2012.

[12] 单铁兵.波浪爬升的机理性探索和半潜式平台气隙响应的关键特性研究[D]. 上海: 上海交通大学, 2013.