自旋-轨道相互作用下X型涡旋光束的传播特性

肖维维，张晗，赵馨颖，马洋，庞晓炎

（1 西北工业大学电子信息学院，西安710072）

（2 陕西师范大学物理学与信息技术学院，西安710119）

0 引言

涡旋光束是一类具有螺旋等相位面的光束，其横截面中心存在相位奇点，光强为零。涡旋光束理论上可以携带具有任意模态的轨道角动量（Orbital Angular Momentum，OAM），并且不同轨道角动量模态的涡旋光束彼此相互正交［1-3］。由于这些特殊性质，涡旋光束已经在无线通信［4-7］、光镊［8-9］、显微镜［10］等领域得到了广泛的研究与应用。然而，涡旋光束的研究主要集中在经典涡旋领域［11-19］，而对于螺旋相位结构非线性变化的非经典涡旋光束的研究较少。

非经典涡旋光束的研究主要集中在二维标量场中［20-28］，比如自由空间中非经典涡旋光束的运动轨迹［21］，非经典涡旋偶极子Airy 波束的相位奇点和能量通量［24］。2020年，LI Jinhong 等［27］对三维矢量光场中高数值孔径系统中涡旋光束的传播特性进行了研究，当入射波为传统非经典波束，即旋转相位因子对强度和相位均有影响的涡旋光束时，传统非经典涡旋光束在实验中不易进行调制。PANG Xiaoyan 等［28］提出了一种新型的非经典涡旋光束（X 型涡旋光束），此类非经典涡旋光束的旋转相位因子只对其光场相位分布有影响，并且通过空间光调制器或者螺旋相位板调制即可产生，并研究表明X 型涡旋光束在紧聚焦系统中会产生一些有异与传统经典涡旋和传统非经典涡旋光束的横向焦移和光强旋转现象，而且其旋转相位梯度对非经典涡旋光束具有调控作用。但是这些研究都未涉及涡旋光束携带的轨道角动量与圆偏振携带的自旋角动量（Spin Angular Momentum，SAM）之间的相互作用（Spin-Orbit Momentum Interactions，SOIs），本文考虑存在SOIs 情况下X型涡旋光束在紧聚焦场中的传播特性，并研究X 型涡旋光束在光场调控中的特点。

1 理论推导与分析

传统非经典涡旋光束在其横截面上通常可以表示为［21-22］

式中，el为LCP 场分量，er为RCP 场分量，ez仍为纵向场分量。后面的结果与讨论主要基于式（4）和式（5）展开。

2 计算结果与讨论

2.1 X 型涡旋光束在焦平面上的横向焦移

2.1.1n=1

本节讨论在n=1，即涡旋光束的拓扑荷数为±1 时，X 型圆偏振涡旋光束在焦平面上的总光场分布特性。入射波为X 型LCP 涡旋光束和X 型RCP 涡旋光在焦平面上的总光场分布如图2所示，这里半孔径角α均取80°。图2（a）、（b）、（c）为LCP 涡旋光，图2（d）、（e）、（f）为RCP 涡旋光，c=0.5，1.0，1.5。由图2 分析可知：1）整体来讲X 型LCP 和X 型RCP 有相同的分布趋势，即相位分布因子c对焦平面上光强的分布有很强的调控作用，横向焦移取决于c的大小，当c=0.5 时，焦平面光强的两个最大值均位于xs轴上，当c=1.5 时，两个最大值均位于ys轴上，当c=1 时，光强沿φs方向均匀分布，即横向焦移现象消失；2）不同圆偏振入射时也具有不同的特性，当入射光为LCP 时，几何焦点处，即光轴处一直是强度最小值点；而入射光为RCP 时，光轴上强度并非光强最小值点，且在c=1 时，强度为最大值，即几何焦点也为实际焦点。

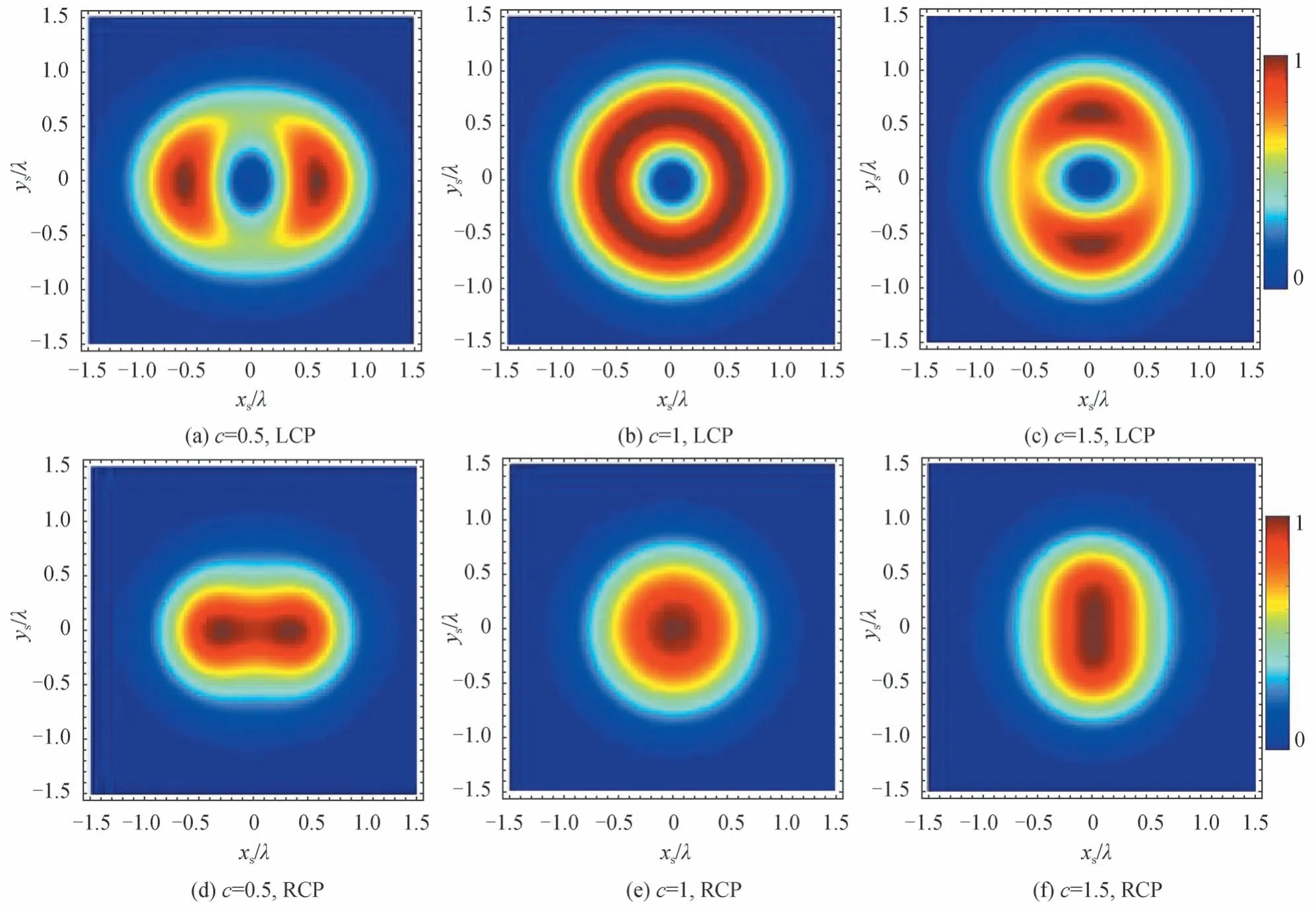
图2 焦平面上的光强随c 变化α=80°，n=1Fig.2 Intensity distribution on the focal plane with the different anisotropic parameters c，where α=80°，n=1

为了更加方便观察c对焦平面光强分布的影响，图3 是入射光为X 型LCP 涡旋光束和X 型RCP 涡旋光束时，焦平面上的强度最大值随c的位置变化（注：由于对称性，此处只展示了一个强度最大值，另一个最大值的位置可由对称性直接求得）。图3 中，英文大写字母代表强度最大值在xs轴上，英文小写字母代表强度最大值在ys轴上，此外五角星表示位于原点处。基于图2 结论，分析图3 可知：1）入射光为LCP 和RCP 时，整体变化趋势是一致的，即当0 ＜c＜1 时，最大值位于xs轴上，而当c＞1 时，最大值移动到ys轴上，且在c=1 时，无横向焦移现象；2）当c的值离1 越远，横向焦移越显著，即最大值离几何焦点越远；3）随着半孔径角α的增大，入射光为LCP 时横向焦移与入射光为RCP 时的横向焦移的差距越大，例如，在α=80°时，当c=0.1 时，入射光为RCP 时最大值位于xs轴0.63λ处，而此时当入射光为LCP 时最大值位于0.55λ处，当c增至0.7 时，入射光为RCP 时最大值位于原点，而入射光为LCP 时最大值位于xs轴0.52λ处。从物理含义上讲，入射光为LCP 和RCP 时聚焦情况的差异主要是由于圆偏振携带SAM 与涡旋光的OAM 在紧聚焦情况下的相互作用，即SOIs 导致的，由于数值孔径越大，SOIs 越强烈（而LCP 与RCP 携带的SAM 方向不同，与OAM 的作用也有所不同），这就导致α越大两者的差异越明显。这一点也可通过改变SAM 与OAM 的相对方向来证明。

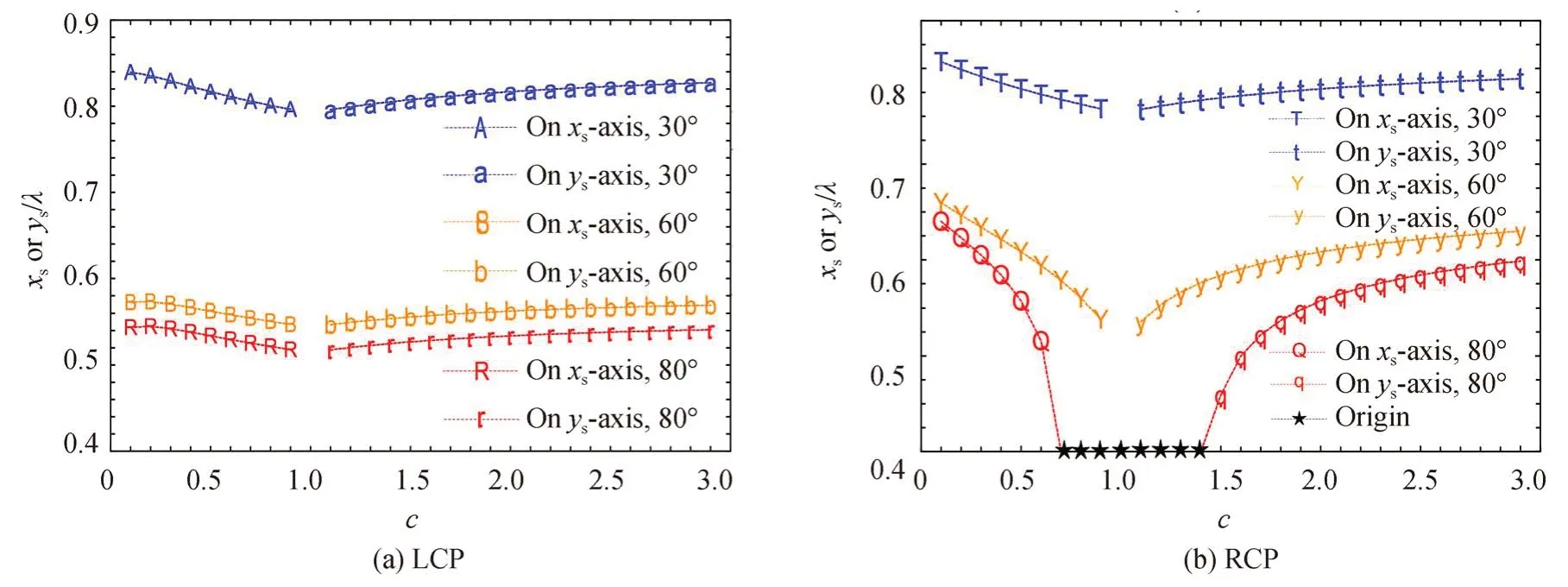
图3 焦平面上光场强度最大值随c 的位置变化，α=30°，60°，80°，n=1Fig.3 Locations of the intensity maxima on the focal plane with the different anisotropic parameters c，where α=30°，60°，80°，n=1

由前面的分析可知，当c的符号改变时，涡旋的拓扑荷数也将改变符号，即涡旋光束的OAM 方向也发生改变。这里取c为负值，仍讨论n=1 时X 型涡旋光束在紧聚焦场中焦平面上的总光场的传播特性。图4 是X 型RCP 涡旋光束（n=1）入射时焦平面上的强度最大值随|c|的位置变化。同样地，图4 中，英文大写表示强度最大值在xs轴上，英文小写字母表示强度最大值在ys轴上。由图3 和图4 对比可得，当c取负值时，入射波为RCP 时横向焦移与c取正值时入射波为LCP 时的横向焦移相同，即只要SAM 与OAM 方向的相对关系不变，横向焦移也不发生改变。

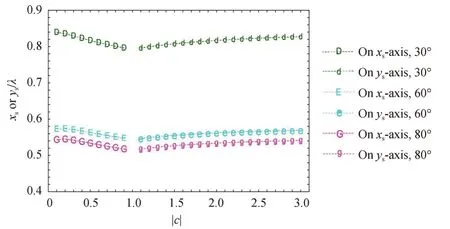
图4 入射光为RCP 时，焦平面上的光场强度最大值随| c|的位置变化，α=30°，60°，80°，n=1，c ＜0Fig.4 Locations of the intensity maxima on the focal plane with the different anisotropic parameters c for the case of RCP，where α=30°，60°，80°，n=1，c ＜0

观察图4 不难发现：当c=1 时，横向焦移消失，同时，最大值将从xs轴转向ys轴，换言之，在圆偏振态下X型涡旋光束在焦平面上的光强最大值有一个相同的轴向转折点csw=1。这一现象实质上是由于圆偏振的非极性产生的，可以通过与入射光为线偏振的情况进行对比说明。图5 为X 型线偏（x偏振）涡旋光束在焦平面上的强度最大值随c的位置变化。由图5 可得线偏振光入射时，X 型涡旋光束在焦平面上强度最大值也是随着c值的增大，逐渐从xs轴转向ys轴，但是与圆偏振情况不同的是，在线偏振光入射时轴向转折点csw会随着α增大逐渐变小并且在c=1 时强度最大值分布在ys轴上。

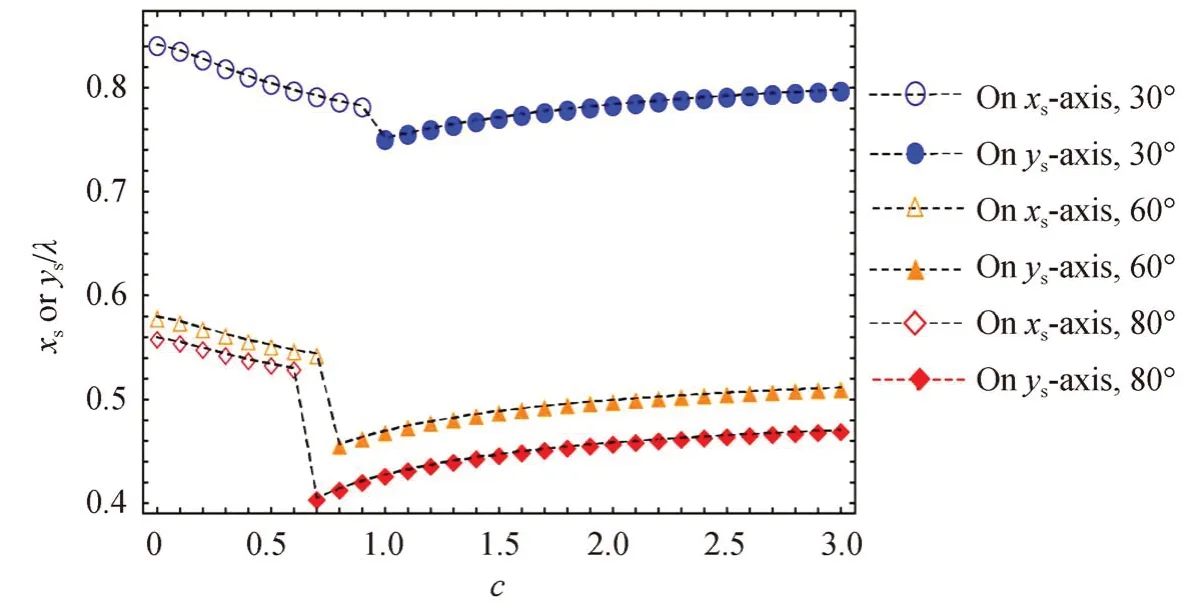
图5 线偏振光入射时，焦平面上光场强度最大值随c 的位置变化，α=30°，60°，80°，n=1Fig.5 Locations of the intensity maxima on the focal plane with the different anisotropic parameters c for the case of linear polarization，where α=30°，60°，80°，n=1

2.1.2n=2

本节将讨论X 型涡旋光束的拓扑荷为±2 时焦平面上的总光场分布特性。理论分析可知，二阶X 型LCP/RCP 涡旋光束入射时，焦平面上的光场分布比一阶更为复杂多样，图6 给出了X 型LCP 和RCP 涡旋光束入射时，焦平面上总光强随相位分布因子c的分布变化情况，此时半孔径角α均取80°。由图6 可知：1）二阶情况下，最大值比一阶变化更加复杂，可以存在一个，两个甚至三个最大值。2）当c很小时，如0.1 和0.3，不管入射波是LCP 还是RCP，强度最大值都分布在中心原点；随着c逐渐增大，其强度逐渐向xs轴方向扩展，当c增大到1 时强度均匀分布，而当c＞1 时强度又逐渐扩散到ys轴上，当c增大到一定程度后强度又回到原点。3）入射波为LCP 和RCP 时聚焦情况不同，例如当c=0.3 时，与入射波为LCP 聚焦情况相比，当入射波为RCP 时，强度明显更加集中在原点周围；当c=3 时，入射波为LCP 时，强度最大值已回归到原点，而入射波为RCP 时，强度最大值仍然分布在ys轴上，并且当c相同时，入射波为LCP 和RCP 时焦平面强度最大值位置是不同的。

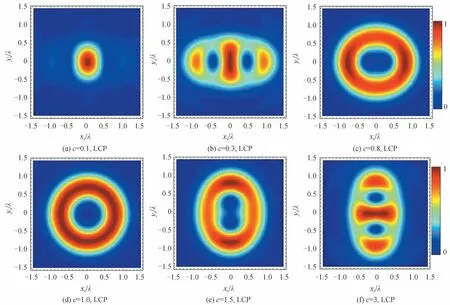
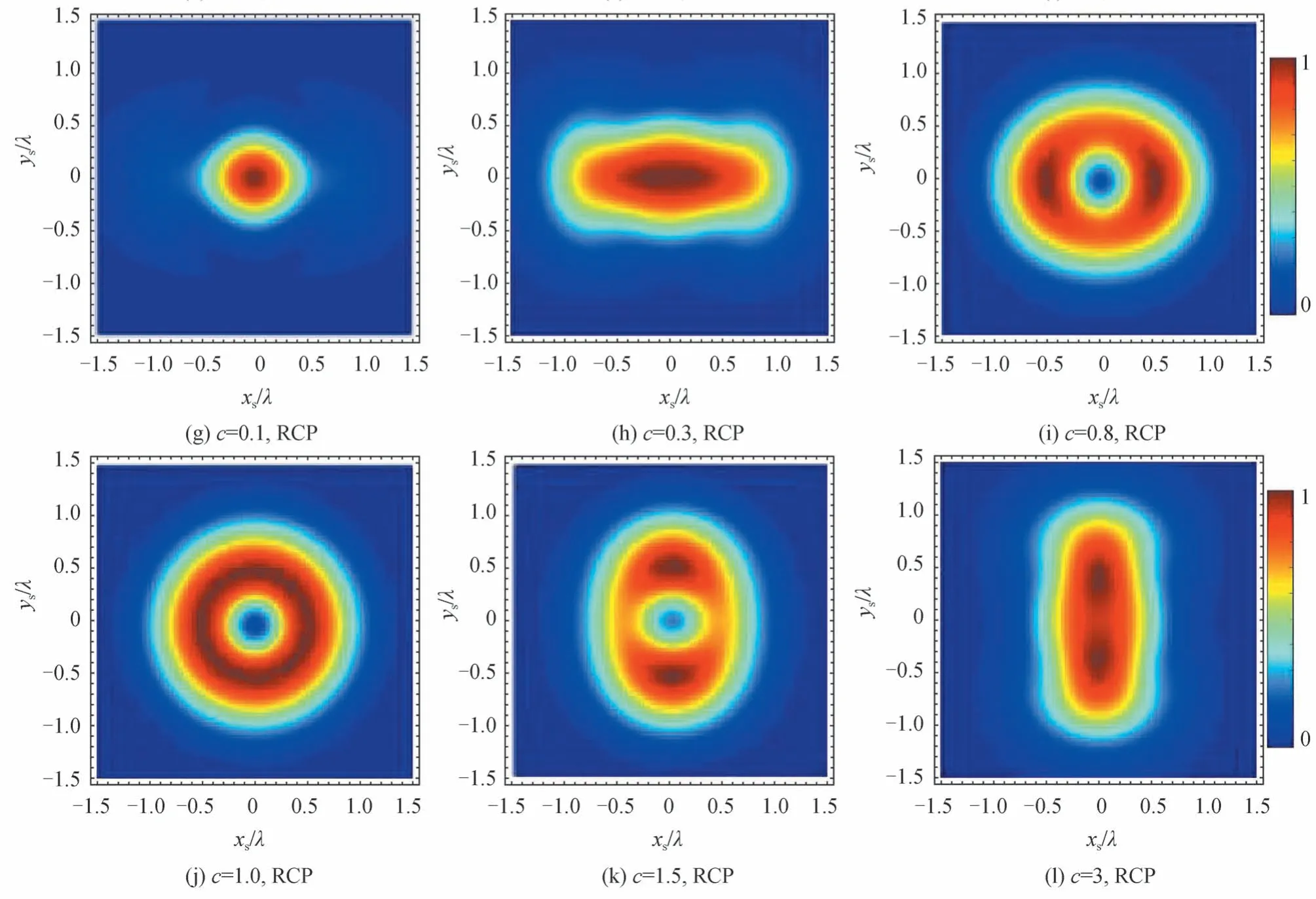
图6 焦平面上的光强随c 的变化，α=80°，n=2Fig.6 Intensity distribution on the focal plane changes with the different anisotropic parameters c，where α=80°，n=2

为了便于观察，图7 给出了X 型LCP 和RCP 涡旋光束入射时焦平面上的强度最大值随c的位置变化情况。类似的，图7 中大写字母表示强度最大值在xs轴上，小写字母表示强度最大值在ys轴上，五角星表示在原点。分析图6 和图7 可以发现：1）在二阶情况下，不管入射波是LCP 还是RCP，它们都有相同的轴向转折点csw=1，且光场在轴向转折点处都呈均匀圆环分布，并且当α较小时基本上都遵循相同的变化规律，即当c≤0.3 时强度最大值均分布在原点，当0.3 ＜c≤0.9 时强度最大值均分布在xs轴上，当1 ＜c≤3 时强度最大值均分布在ys轴上；2）当α和c取值较大时，入射波为LCP 和RCP 时焦平面上的光强有较大差异：当α=60°时，入射波为LCP 时强度最大值由ys轴回到原点的转折点是csw=2.8，而入射波为RCP 时转折点是csw=2.9，当α=80°时，入射波为LCP 时强度最大值由ys轴回到原点的转折点是csw=2.8，而入射波为RCP，当1 ＜c≤3 时强度最大值始终未回归原点，此外，随着α逐渐增大，入射波为LCP 和RCP 时强度最大值之间的距离逐渐增大。这些差异的本质是SOIs 作用的结果。

图7 焦平面上的光强随c 的变化，α=30°，60°，80°，n=2Fig.7 Locations of the intensity maxima on the focal plane with the different anisotropic parameters c，where α=30°，60°，80°，n=2

图8 给出了X 型线偏振涡旋光束入射时在焦平面上的强度最大值随c的位置变化情况。由图8 可知，入射波为线偏振时在焦平面上的强度最大值也遵循先在原点，然后扩散到xs轴上，再移动到ys轴上，最后又回到原点的规律，其强度最大值的轴向转折点会随着半孔径角α的增大逐渐减小，但是入射光为圆偏振时轴向转折点csw均为1，并且在轴向转折点处光强都沿角向均匀分布。偏振态的极性分布导致了这一现象的产生。

2.2 X 型涡旋光束沿传播方向的场分布

上一节讨论了X 型LCP/RCP 涡旋光束在紧聚焦场中焦平面上的光强分布，本节讨论它们在紧聚焦场中沿传播方向的变化情况。为了不失一般性，这里相位因子c取0.3，其它取值可进行类比分析。需要说明的是，当c=1 时，X 型涡旋退化为经典涡旋，本节讨论的X 型涡旋光束的传播行为将不再发生。

2.2.1n=1

首先，讨论当n=1 时X 型LCP 和RCP 涡旋光束在紧聚焦光场中沿传播方向的光场分布。图9 是X 型LCP 和RCP 涡旋光束沿传播方向的总光强分布，这里zs=−2λ，0，+2λ，半孔径角均为80°，相位因子c均为0.3。由图9 可知，入射波不管是LCP 还是RCP，当zs=0 时，其两个强度最大值（此处定义为A，B两点）对称分布在xs轴上，当zs=±2λ时强度最大值不再分布在xs轴上，而是沿着传播方向出现偏离轴的旋转现象。

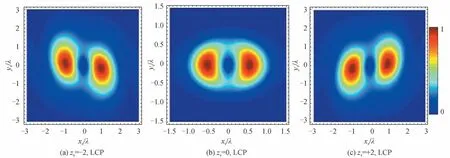
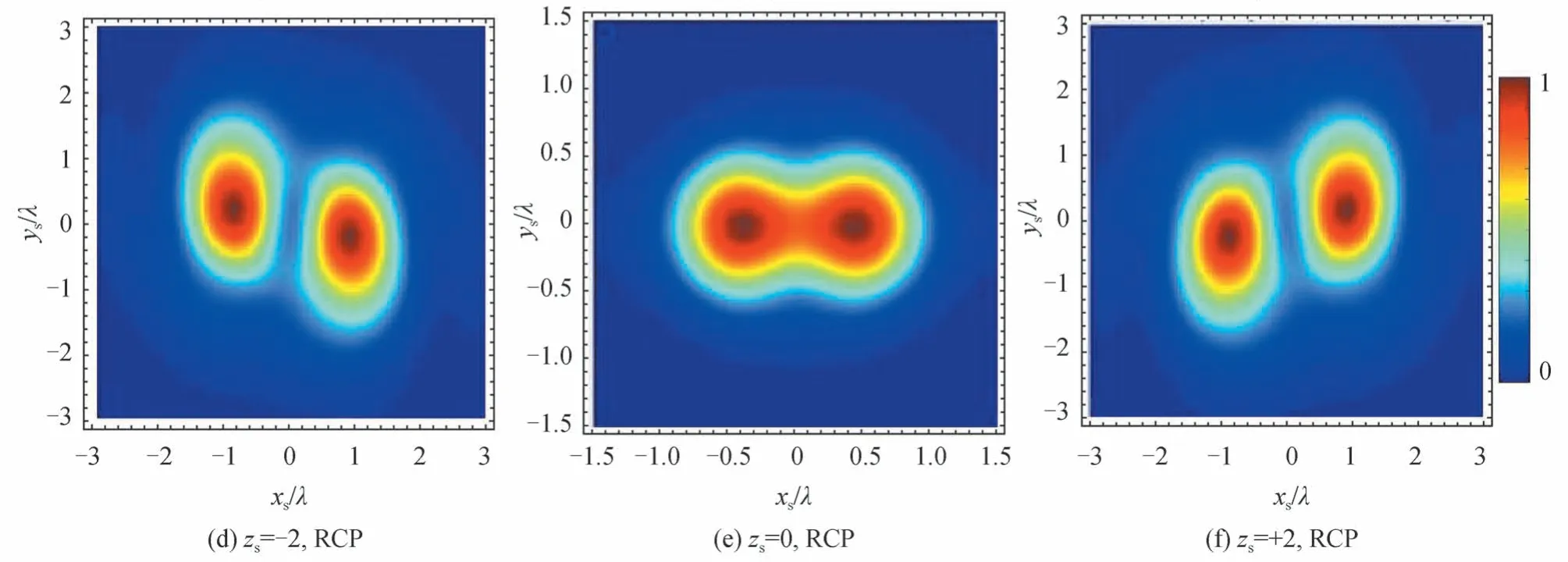
图9 光强沿传播方向的分布，其中zs 单位为λ，α=80°，n=1，c=0.3Fig.9 Intensity distribution on the transverse planes along the propagation direction，where the unit of zs is λ，α=80°，n=1，c=0.3

为了观察这种旋转现象，图10 给出了入射波为LCP、RCP 以及线偏振入射时强度最大值的方位角随传播距离的变化情况（−10λ≤zs≤10λ）。分析图10 可知，不管是何种偏振态的入射波，其强度最大值的旋转角度范围均为−50°～50°，并且沿着传播方向均为逆时针旋转；入射波为线偏振时旋转角度变化趋势位于入射波为LCP 和RCP的中间并且与LCP 和RCP 的旋转角度差距甚小，可见沿传播轴方向的光场旋转特性受入射波偏振态的影响较小。比较入射波为LCP 和RCP时沿传播方向强度最大值的旋转角度可知，其旋转角度是存在差距的，但旋转角度差距会随着传播距离的增大而减小。

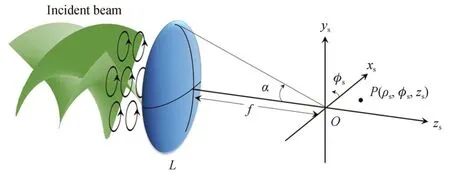
图1 入射光场为X 型涡旋光的紧聚焦系统Fig.1 A tightly focusing system with a X-type vortex beam as the incident field

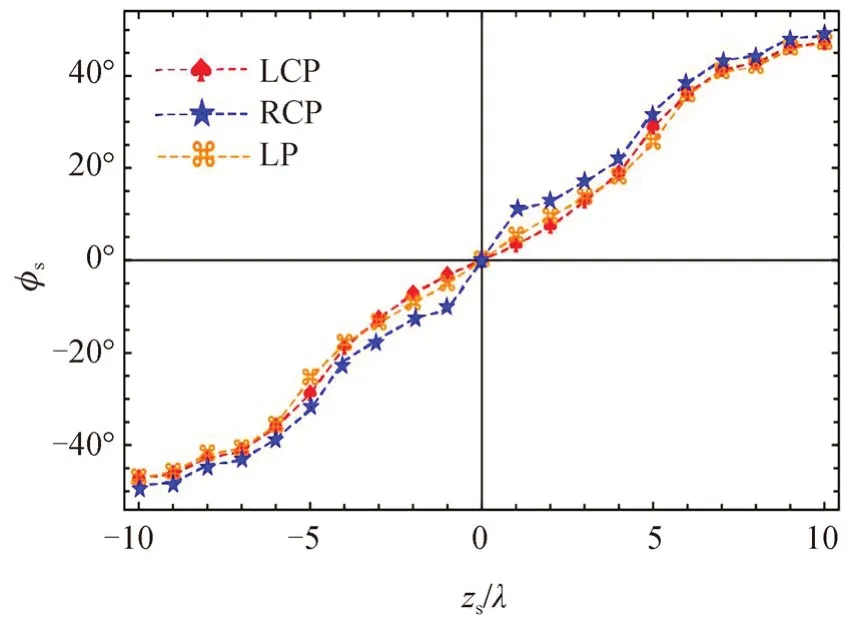
图10 光强最大值沿传播方向的方位角，α=80°，n=1，c=0.3Fig.10 Variation of the azimuthal angles of the intensity maxima along the propagation direction，here α=80°，n=1，c=0.3

2.2.2n=2

上一小节讨论了n=1 时光场沿传播方向的传播特性，本节讨论当n=2 时X 型LCP/RCP 涡旋光束在紧聚焦场中沿传播轴的光场分布。图11 为入射波为LCP 和RCP 时沿传播方向的总光强以及LCP 和RCP 的场分量（el，er）相位分布（−10λ≤zs≤10λ），半孔径角均为80°，相位因子c均为0.3。由图11 总光强分布可知：入射波不管是LCP 还是RCP，当zs=0 时，其强度最大值在原点即几何焦点；当zs=±0.5λ时，入射波为LCP 时强度最大值在原点，并且存在旋转现象，入射波为RCP 时强度最大值分离为两个并且出现旋转现象；当zs=+1λ时，入射波为LCP 和RCP 时强度最大值都分离为两个并且出现旋转现象。从图11 总光强所对应的主要场分量el，er的相位分布可知，其场分量相位均存在两个主要的涡旋点，当zs=0 时两个主要涡旋点对称分布在xs轴上，当zs≠0 时涡旋点具有与强度最大值类似的旋转现象。

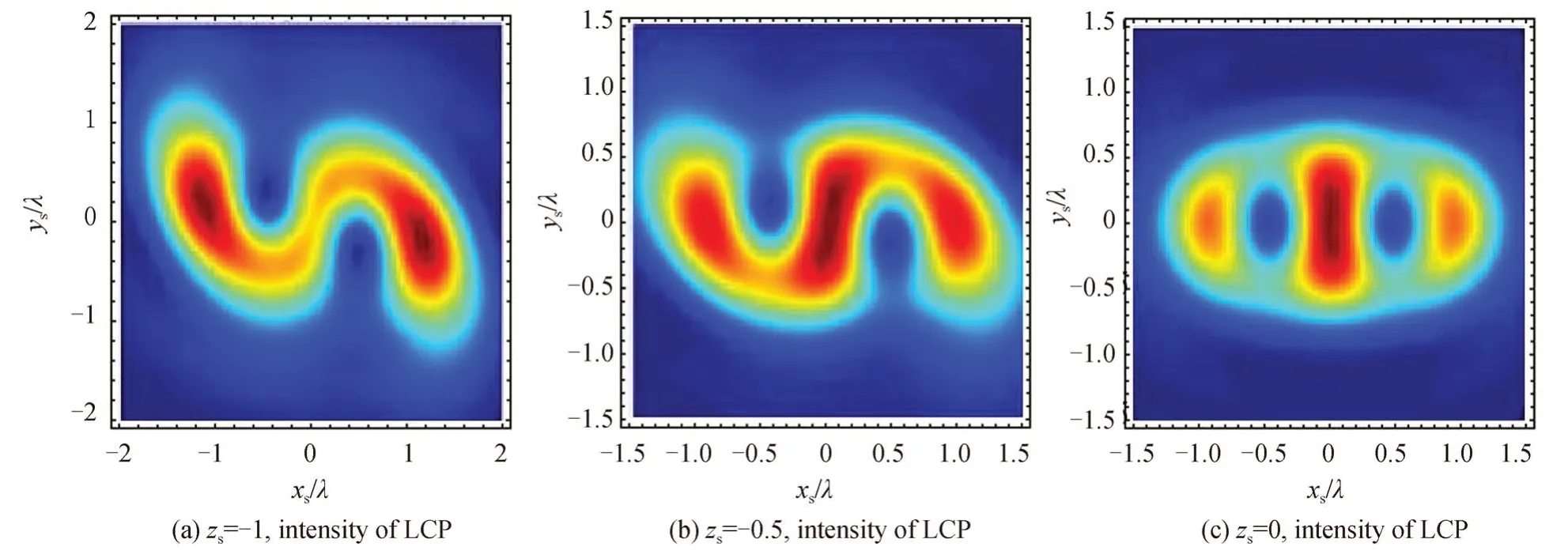
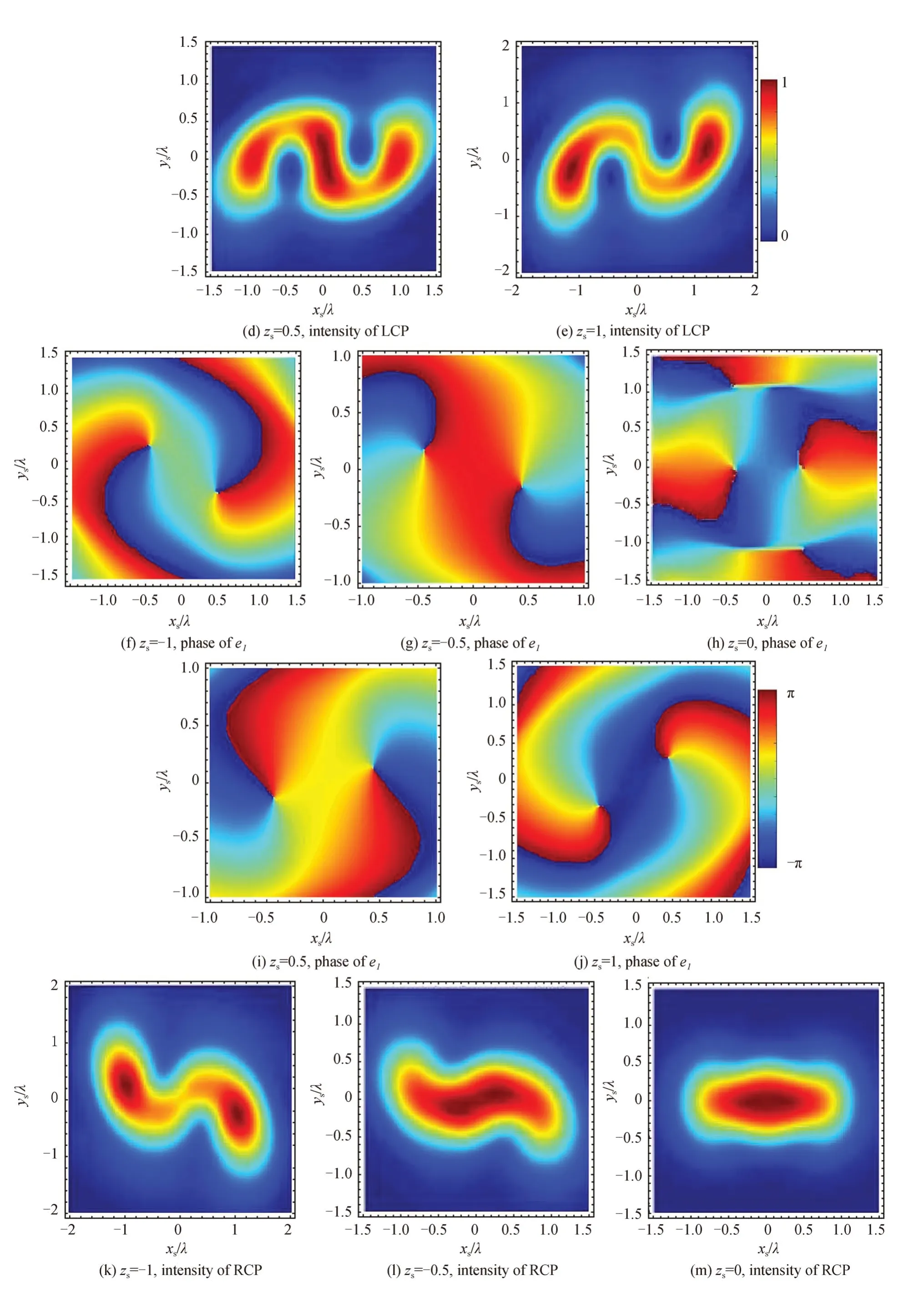
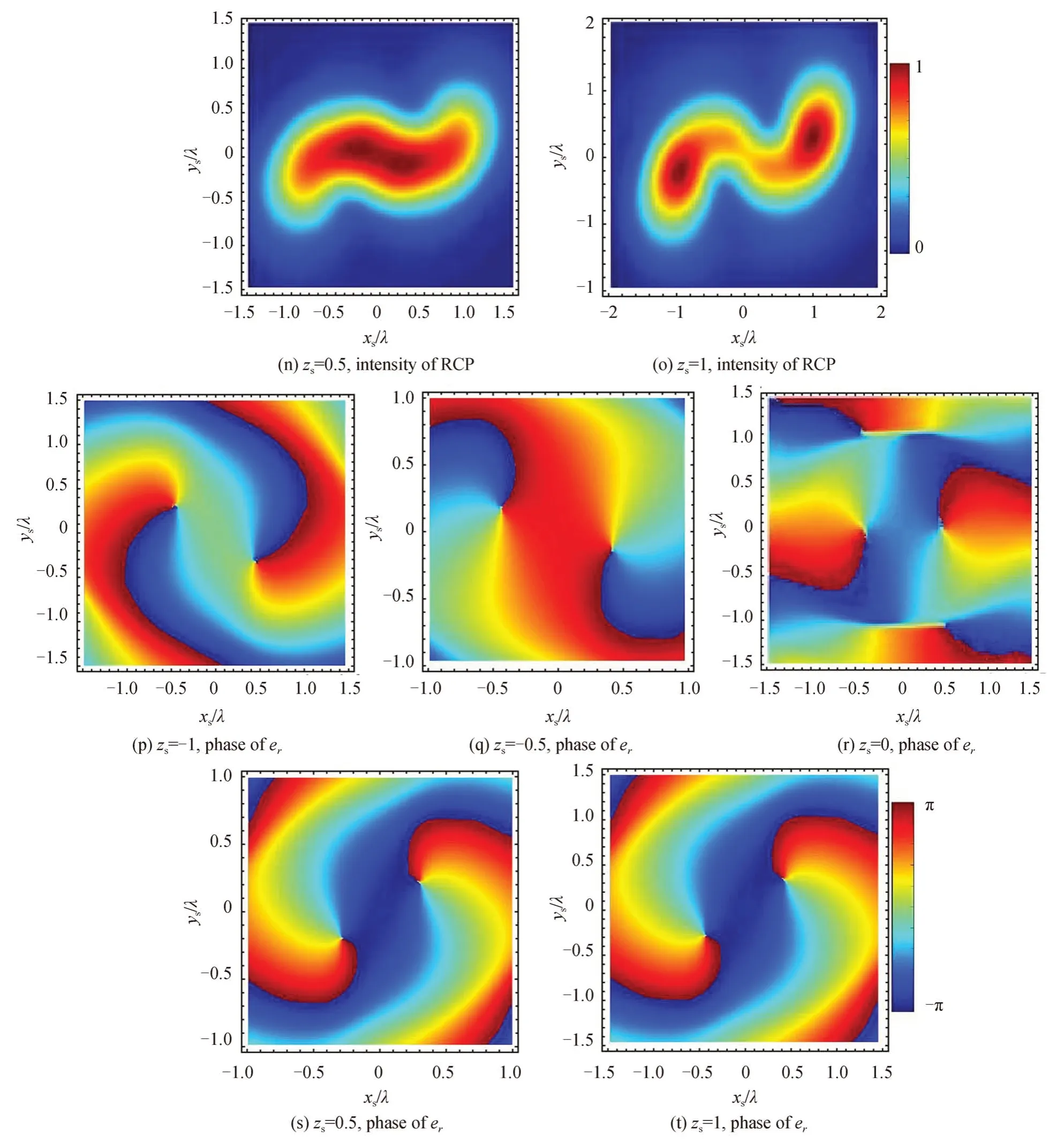
图11 传播方向上光强和相应的主要场分量相位分布，其中zs 单位为λ，α=80°，n=2，c=0.3Fig.11 The intensity distribution and the corresponding phase of the main field component with the beam propagation.Here the unit of zs is λ，α=80°，n=2，c=0.3

为了观察光强的旋转现象，入射波为LCP 和RCP 时传播方向光强最大值的方位角变化情况如图12所示（−10λ≤zs≤10λ），图中半孔径角α=80°，蓝色代表入射波为LCP，红色代表入射波为RCP。由图12 可知：1）当n=2 时，入射波为LCP 和RCP 时强度最大值沿传播轴的旋转角度范围都为−50°～50°，沿着传播方向逆时针旋转；2）当zs=0 时，正如前一节的分析，当c=0.3 时无论入射波为LCP 还是RCP，在焦平面上都不存在横向焦移现象，即强度最大值无旋转角度，因此图12 中在zs=0 时不连续，而当n=1 时，入射波为LCP 和RCP 时，沿传播轴方向强度最大值的方位角曲线均是连续的；3）当入射波为LCP 和RCP 时，强度最大值的具体位置仍具有差异，越靠近焦平面差异性就越明显。这种差异性的物理本质是SOIs 作用的结果，也可通过入射波为LCP 和RCP 时三个场分量的分布情况进行讨论。

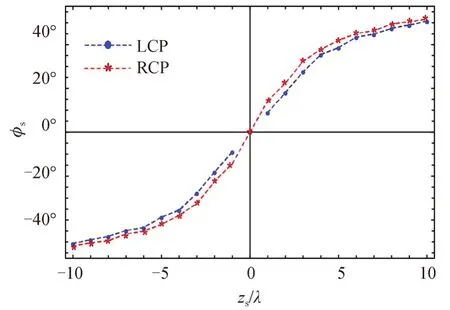
图12 光强最大值沿传播方向的方位角变化，α=80°，n=2，c=0.3Fig.12 Variation of the azimuthal angles of the intensity maxima along the propagation direction，here α=80°，n=2，c=0.3

当入射波为LCP 和RCP 时X 型涡旋光束在聚焦区域的三个场分量el，er，ez的强度和相位分布如图13所示，图13（a）、（b）、（c）分别为入射波为LCP 时el，er，ez强度分布，图13（g）、（h）、（i）分别为入射波为RCP 时el，er，ez的强度分布；图13（d）、（e）、（f）分别为入射波为LCP 时el，er，ez相位分布，图13（j）、（k）、（l）分别为入射波为RCP 时el，er，ez的相位分布，传播距离zs=−1λ，半孔径角α=80°，相位因子c=0.3。分析图13 可知：1）入射波为LCP 时对总光强起主要作用的是el，ez两个分量（见图13（a）、（b）、（c）），而入射波为RCP 时对总光强起主要作用的是er，ez两个分量（见图13（g）、（h）、（i））；2）入射波为LCP 时el分量的强度、相位分布和入射波为RCP 时er强度、相位分布相同，两者的涡旋点的位置也相同（标记为SM和SN）。众所周知，涡旋点的位置对涡旋所在场分量的光强分布起着重要的作用，因此为了观察这两个分量涡旋点（SM和SN）沿传播方向的传播特性，图14 展示了沿传播方向入射波为LCP 时el分量的涡旋点位置（方位角）和入射波为RCP时er分量的涡旋点位置，图中半孔径角α=80°，相位因子c=0.3（注：由于对称性，只展示了一对涡旋点中的一个）。由图14 可得，这两种情况下涡旋点沿传播方向均为逆时针旋转，并且旋转角度范围均为−65°～65°。这说明，入射波为LCP 时el分量和入射波为RCP 时er分量对总光强分布具有相同的影响，因此两种情况下最大光强分布的差异主要是由ez分量的差异产生的；3）入射波为LCP 时ez分量的相位分布有三个涡旋点，而入射波为RCP 时仅有一个中心涡旋点。基于以上分析，从场分量角度来讲，不同的ez分量的相位分布或者是其相位涡旋点分布，是导致X 型LCP 和RCP 涡旋光束在传播方向上光强最大值旋转角度差异的主要因素。

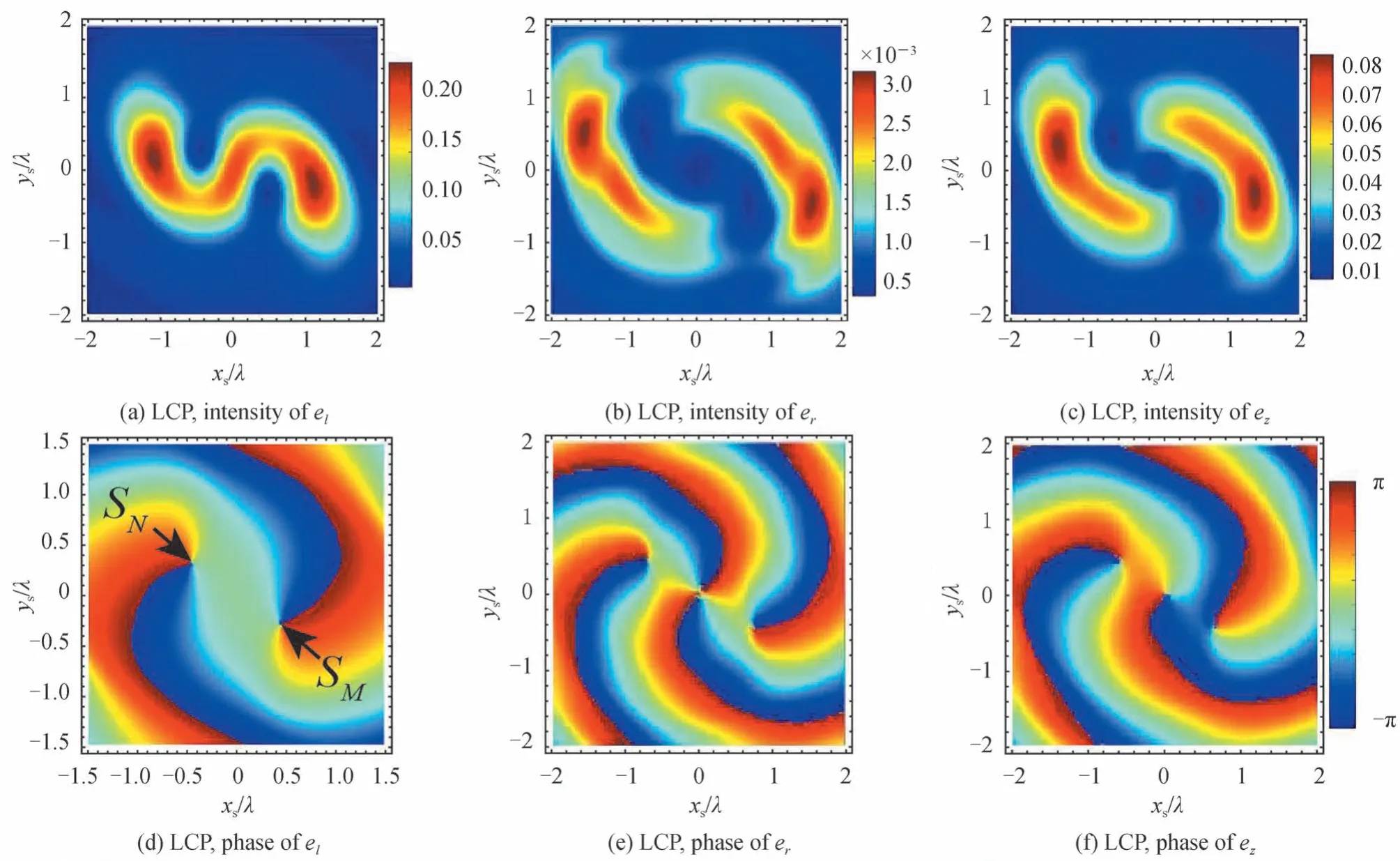
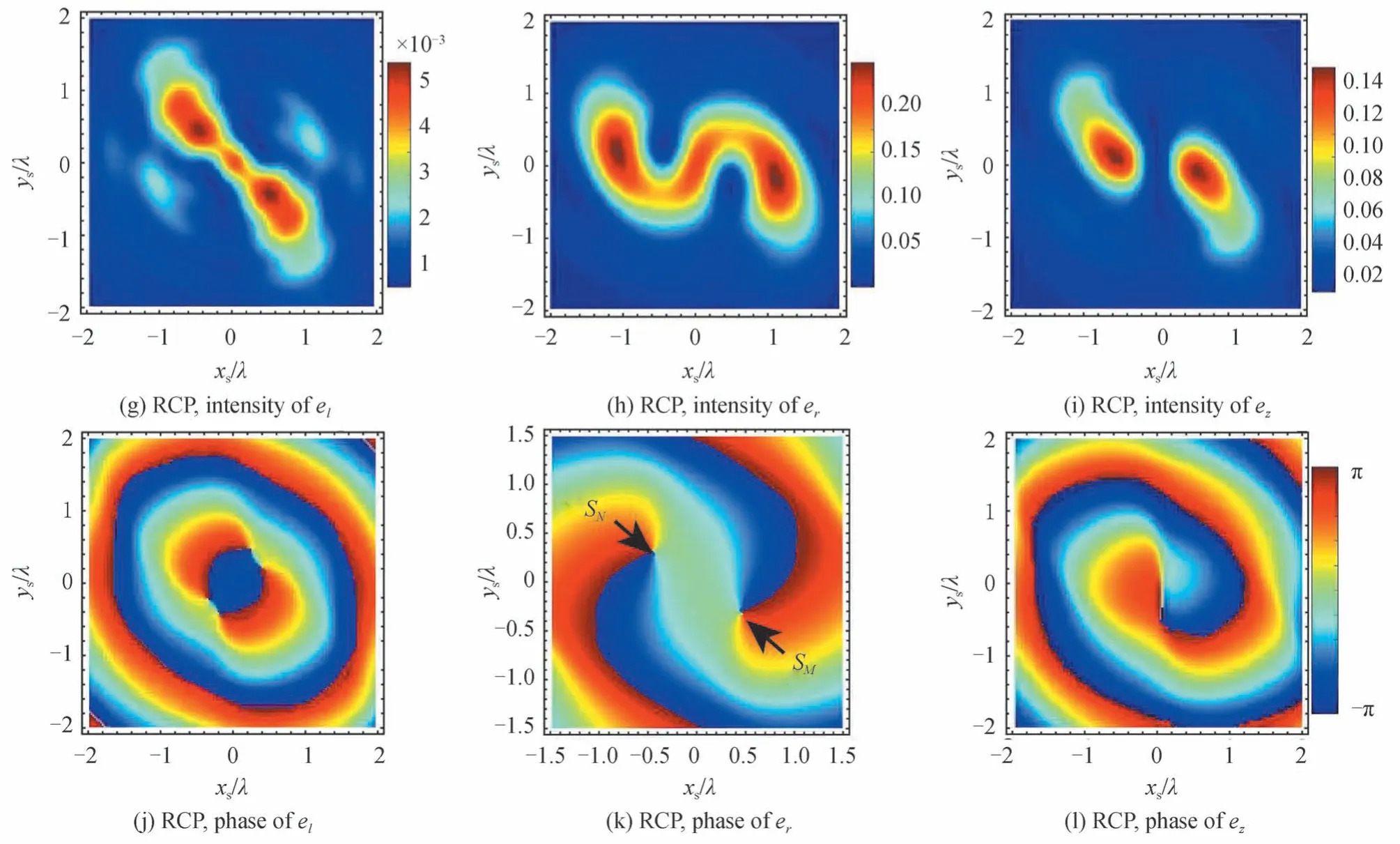
图13 传播方向el，er，ez 三个分量强度和相位分布，α=80°，n=2，c=0.3Fig.13 Field component distribution with the beam propagation，here α=80°，n=2，c=0.3

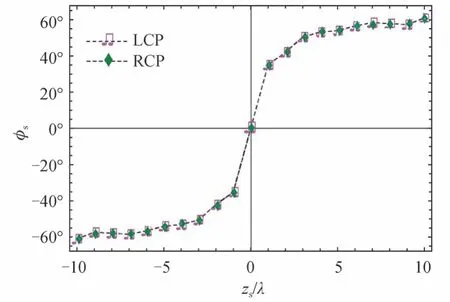
图14 LCP 和RCP 入射时，el/er 分量涡旋点沿传播方向的方位角变化，α=80°，n=2，c=0.3Fig.14 Variation of the azimuthal angles of the vortices of el/er components along the propagation direction for the cases of LCP and RCP，here α=80°，n=2，c=0.3

3 结论

研究了在SOIs 作用下，X 型涡旋光束在高数值孔径系统中的光场传播特性，并得到了X 型涡旋光束相位分布因子c，半孔径角α，偏振态和拓扑荷数等对光强分布的调控作用。研究发现：1）当相位分布因子|c|≠1 时，焦平面上存在横向焦移，沿传播方向的光强分布呈现逆时针旋转现象，并且旋转方向和整体的旋转角度不受入射波偏振态的影响；2）入射波为LCP 和RCP 时，在焦平面和传播方向上光强分布出现差异，本质上是由SOIs 导致的；3）无论入射波为LCP 还是RCP，X 型涡旋光束在焦平面上强度最大值的轴向转折点均为csw=1，这与线偏振态下csw≤1（且随孔径角可变）不同，这是入射波偏振态使得光场非极性分布的结果；4）当X 型涡旋光束为二阶时，在与入射波相同偏振态的场分量中，会出现两个主要涡旋点，这两个涡旋点也会沿传播方向逆时针旋转，并且入射波为LCP 和RCP 时两个主要涡旋点位置相同，旋转一致；二阶情况下，入射波为LCP 和RCP 时纵向场的不同导致了光强分布的差异。本文研究为三维光场的调控提出了思路和方法。