波浪驱动下箱式浮体运动响应及受力的数值研究
2022-03-18陈善群张龙珠
陈善群,张龙珠,廖 斌
(安徽工程大学 建筑工程学院,安徽 芜湖 241000)
1 研究背景
箱式浮体作为一种常见的浮体类型,在海洋及河流等大型水体中较为常见,诸如浮标、浮桥以及大型网箱等主体外形大多设计为箱式。由于箱式浮体在水体中易受波浪的驱动而产生受力以及运动响应,具体体现为包括垂向、横向和纵向的3个平移运动,以及包括偏航、俯仰和横摇转动的3个旋转运动。当波浪驱动作用较强时,箱式浮体甚至会倾覆,产生多浮体之间相互拍击现象,直接影响浮体的稳定性,进而危及浮体上设备的正常工作,以及工作人员的人身安全[1]。同时,波浪驱动下浮体运动响应及所受波浪力的研究涉及到波浪自由面精细刻画、波浪与浮体流固耦合求解等一系列时下热门学术问题。因此,研究波浪驱动下箱式浮体运动响应以及所受波浪力具有较为重要的工程意义和学术价值。
国内外对于波浪驱动下浮体的运动响应及所受波浪力的研究由来已久,但目前的成果大多集中于波浪驱动单个浮体方面。试验研究方面:Zhao和Hu[2]观测了单个倒T型浮体在规则波、聚焦波驱动下的运动响应,并获取了浮体摇荡角度以及起伏位移等数据;He等[3]对单个箱式浮体在波浪驱动下的运动图像进行了实时拍摄,获得了不同波高和周期条件下浮体在波浪中的非线性运动响应数据;Wang等[4]对规则和不规则波浪驱动下单个沙漏型浮体的运动响应进行了试验,获取了沙漏型浮体摇摆周期、黏性阻尼等运动响应数据;Ji等[5]对单个矩形浮式防波堤在波浪驱动下的运动响应及所受波浪力进行了试验,对浮体所受的系泊力和三自由度运动响应进行了系统分析;Yang等[6]设计了一种新型的压载水浮式防波堤,并研究了该浮体在二维规则波驱动下的流体力学效率和运动响应。数值研究方面:Wu和Hu[7]采用二维三叉树方法生成动网格,并结合有限元方法数值研究了非线性波浪驱动下单个漂浮拖曳罐的运动响应;Hu等[8]开发了一套计算流体力学程序(AMAZON-SC),数值分析了规则波浪驱动下单个波能转换器的垂向受力以及运动响应;Jeong和Lee[9]改进了标记密度法,并发展了一种数值模型来模拟浮体在波浪驱动下的运动响应,计算获得的海上平台运动响应数据与试验相符;Omidvar等[10]开发了一种质量分布可变的光滑粒子流体动力学方法(Smoothed Particle Hydrodynamics,简称SPH),并数值研究了波浪驱动下二维楔形和三维圆锥形浮体的运动响应;曹文瑾等[11]采用移动粒子半隐式方法(Moving Particle Semi-implicit,简称MPS)对波浪驱动下单个长板型浮体运动响应进行了数值分析。
相较于单个浮体运动响应及所受波浪力研究的丰富成果,波浪驱动下多个浮体运动响应及所受波浪力相关研究成果较少。较为具有代表性的工作有:谢楠和郜焕秋[12]应用三维线性势流理论计算了2个箱式浮体以及2条船水面补给时的水动力作用结果;孙丽娜[13]基于浮体与流体的耦合作用以及浮体间的接触算法,数值研究了多个浮体之间的接触碰撞问题;Zhang等[14]对不同排列布局条件下波浪与多个浮体之间的相互作用进行了系统研究,并对波能转换器阵列布局的优化提供了有效的参考信息。虽然以上研究对于波浪驱动下多个浮体的运动响应及所受波浪力均有涉及,但对于各浮体之间运动响应及所受波浪力影响因素的系统性分析较少,相关作用机制还需进一步发掘。
针对以上研究的不足,鉴于无网格方法在处理流固耦合问题上的先天优势,本文拟选取SPH方法对波浪驱动下单个箱式浮体运动响应及所受波浪力进行系统研究,并通过不同Keulegan-Carpenter(简称KC)数工况来发掘浮体运动响应与所受波浪力之间的影响机制。在此基础上,本文系统研究波浪驱动下不同浮体间距工况中2个箱式浮体的运动响应,并深入对比分析单个和2个箱式浮体工况的相关数据,发掘浮体之间间距对上游浮体和下游浮体运动响应的影响机制,为浮体设计和水动力响应研究提供有价值的参考信息。
2 数值模型
2.1 SPH方法
SPH方法是一种拉格朗日无网格粒子方法。用于流体动力学模拟时,SPH方法使用一组粒子离散化连续介质,并根据粒子周围的物理特性,在每个时间步中参考每个粒子的所在位置对离散的Navier-Stokes方程进行局部积分,得出每个粒子新的物理量。然后,每个粒子根据新的物理量更新得到新的位置,模拟粒子的实时移动,进而实现模拟流体的运动过程。每个粒子有一个相邻粒子的集合,此集合通常被称为紧支域(二维情况下为圆形,三维情况下为球形),基于距离函数决定,相关的特征长度或平滑长度通常用h表示。
SPH方法利用基于插值或加权函数的积分方程,将连续介质流体力学的守恒定律从偏微分形式转化为适用于粒子模拟的形式,通常这种插值或加权函数被称为核函数。基于核函数,SPH粒子近似理论的表达式可以写为
(1)
式中:F(r)为粒子物理属性函数;r为粒子的矢径,下标i表示任意粒子,下标j为该粒子的相邻粒子;mj为相邻粒子的质量;ρj为相邻粒子的密度;W(r,h)为核函数,表达式为
0≤q≤2 。
(2)
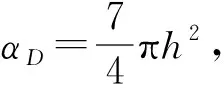
2.2 SPH方法模拟流体运动的控制方程
基于粒子近似理论,SPH方法模拟流体运动的控制方程可表述为:
连续介质动量守恒方程

(3)
连续性方程
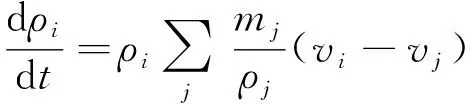
(4)
状态方程
(5)
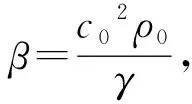
2.3 人工黏性项
SPH方法在模拟流体运动时,流场中容易产生非物理性振荡,从而导致数值计算不稳定以及精度下降。此时,往往需要借助数值稳定手段来保证数值计算的稳定进行。施加人工黏性项是目前较为有效的手段之一,本文采用Monaghan[15]提出的人工黏性项,表达式为
其中,
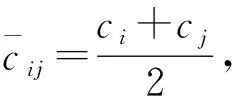
施加人工黏性项后,动量守恒方程(式(3))可写为

(7)
2.4 密度耗散项
SPH方法中当流场密度视为弱可压缩时,粒子密度易出现高频振荡,从而引发流场内部的压力波动。为消除密度波动带来的不利影响,本文在连续性方程中添加由Fourtakas[16]提出的密度耗散项,添加后的连续性方程(式(4))表达式为
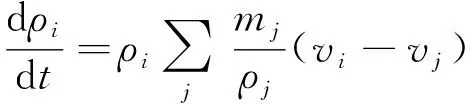
(8)
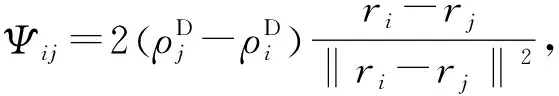
2.5 时域积分格式
本文使用具有二阶精度的辛-Verlet时域积分格式[17]对流体运动控制方程进行时间迭代求解,表达式为
(9)
时间步长Δt可变,其控制方程为
式中:Δtf为满足惯性条件的最小时间步长;Δtcv为满足黏性条件的最小时间步长;CCFL为Courant-Friedrichs-Lewy常数,本文取值0.2。
2.6 流体驱动物体运动边界条件
为数值模拟水体驱动下浮体的运动过程,本文需建立流体驱动物体运动边界条件以求解出物体每一时间步的速度、角速度等运动要素,具体思路如图1所示。
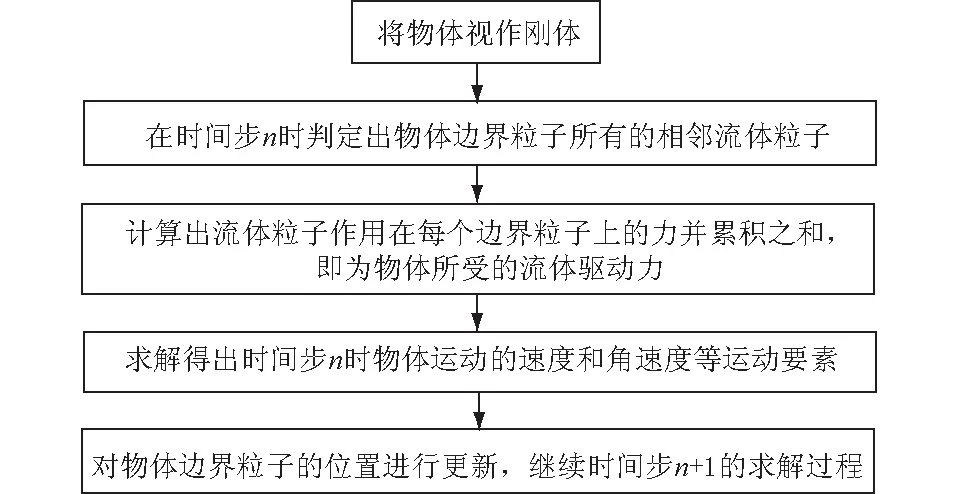
图1 流体驱动物体运动边界条件求解物体运动过程流程Fig.1 Flowchart of solving motions of objects via fluid-driven boundary conditions of objects
物体运动要素的求解使用刚体动力学的基本方程式,表达式为:
(11)
(12)
式中:M为物体的质量;v为物体移动的速度;mb为边界粒子b的质量;fb为边界粒子b所受的单位质量力;I为物体相对于质心的转动惯量;ω为物体转动的角速度;rb为边界粒子b的位置;C0为物体的质心位置。
边界粒子位置更新基于式(13)求得,即
vb=v+ω(rb-C0) 。
(13)
式中vb为边界粒子的速度矢量。
2.7 数值算例
波浪驱动下箱式浮体六自由度运动示意如图2所示。考虑到本文选取的造波方式为造波板活塞式往复运动,此种波浪条件下箱式浮体六自由度运动以x方向的纵向运动(surge)、z方向的垂向运动(heave)以及绕y轴的俯仰转动(pitch)为主,其余3种运动均相对不明显[18]。本文选取二维波浪数值水槽计算模型来研究波浪驱动下箱式浮体的运动响应及所受波浪力,考虑到需采用单个箱式浮体工况作为数据参考和机理分析之用,计算模型分单个和2个箱式浮体,分别如图3(a)和图3(b)所示。波浪数值水槽长度区间为[0,18.0]m,其中[0,7.5]m为工作区,[7.5,18.0]m为消波区,高度区间为[0,0.75]m,静水深度为0.4 m,图中示例的箱式浮体尺寸为长×高=l×H=0.3 m×0.2 m,密度为500 kg/m3。数值水槽内粒子间距Δx=0.005 m,粒子总数为137 523。初始时刻,浮体重心高度与水平面持平。造波板持续水平往复运动进行造波,运动位移与生成二阶斯托克斯波的周期和波高等因素相关,满足Madsen造波理论[19]。
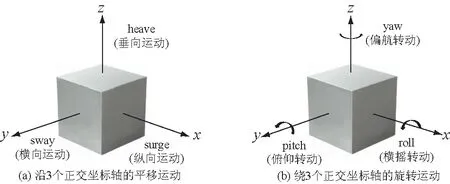
图2 箱式浮体六自由度运动示意Fig.2 Motions of a freely floating rectangle box with six degrees of freedom
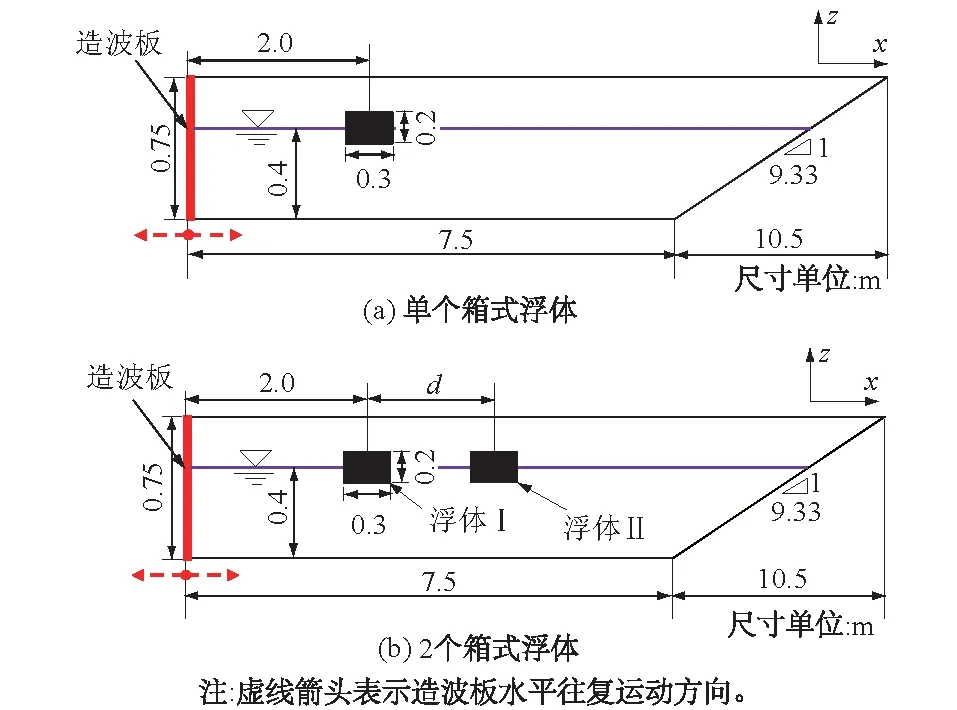
图3 波浪驱动下箱式浮体运动响应及所受波浪力计算模型Fig.3 Computational model of motions and wave forces of wave-driven floating rectangle boxes
为系统研究KC数以及2个浮体间距对箱式浮体运动响应及所受波浪力的影响规律,表1列出了本文选取的单个和2个箱式浮体计算工况。其中,S1—S3为单个箱式浮体工况,T1—T4为2个箱式浮体工况。为建立统一规范的计算条件,这里将浮体间距d无量纲化为δ,δ=d/l,l为箱式浮体的长度。KC数的表达式为:KC=2πa/H,其中a为生成波浪的波幅,H为箱式浮体垂直于波浪来流方向的高度。需要说明的是,本文中箱体尺寸以及密度在各个计算工况中均保持一致,不同KC数工况由波浪周期T保持不变时调节波浪波幅a来实现。另外,为表述简洁,下文中将上游和下游浮体分别简称为浮体Ⅰ和浮体Ⅱ。
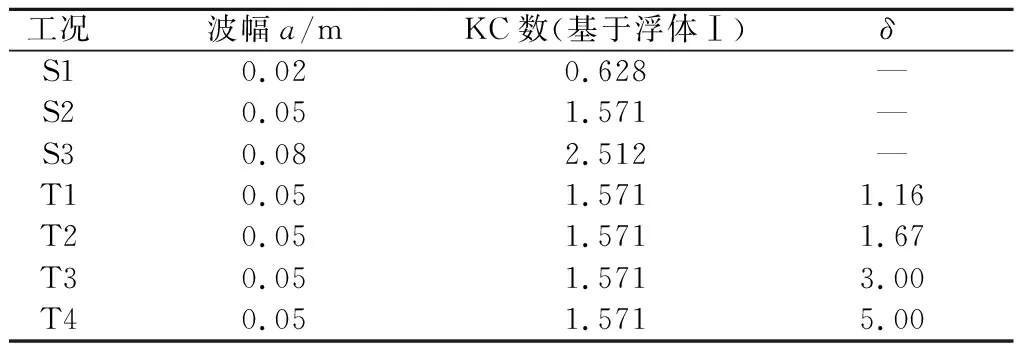
表1 单个和2个箱式浮体的计算工况Table 1 Numerical cases for the single and two floating rectangle boxes
3 结果分析与讨论
3.1 波浪驱动单个箱式浮体运动响应及所受波浪力
以S2工况为典型算例,对波浪驱动下单个箱式浮体运动响应及所受波浪力进行深入剖析。图4给出了S2工况中波浪驱动下单个箱式浮体运动响应随时间演化曲线,并与Ren等[18]的试验结果进行对比。
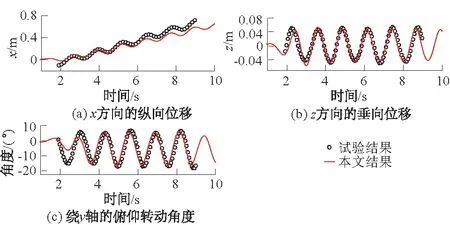
图4 S2工况下单个箱式浮体运动响应随时间的演化Fig.4 Motions of a single floating rectangle box versus time in case S2
从图4可以看出,波浪驱动下单个箱式浮体在x方向纵向位移、z方向垂向位移以及绕y轴俯仰转动角度三方面的运动响应数值计算曲线与试验结果均较为吻合,说明本文采用的SPH数值模型在研究波浪驱动下的浮体运动方面具有较高的精确度和较好的适用性。进一步分析S2工况下单个箱体在波浪中的运动响应可知,z方向的垂向位移以及绕y轴俯仰转动角度呈现明显的周期性波动,波动周期与波浪周期T较为接近;箱式浮体z方向的垂向最大位移与波浪简谐振动幅度(波幅)较为接近,绕y轴的俯仰转动时顺时针转动幅度要稍大于逆时针;而x方向的纵向位移随时间的增长呈现规律的波动性增加趋势。在箱式浮体在波浪中的运动响应与试验结果相吻合的基础上,本文获取了S2工况下单个箱式浮体所受的波浪力,结果如图5所示。二维条件下箱体所受的波浪力大小可通过F/L计算,L表示浮体的湿周。其中,Fx和Fz分别表示箱式浮体x和z方向所受的波浪力。从图5可以看出,箱式浮体x和z方向所受波浪力曲线同样呈现较为规律的周期性变化,波动周期与波浪周期T同样较为接近,且在S2工况下z方向所受波浪力较x方向要大。
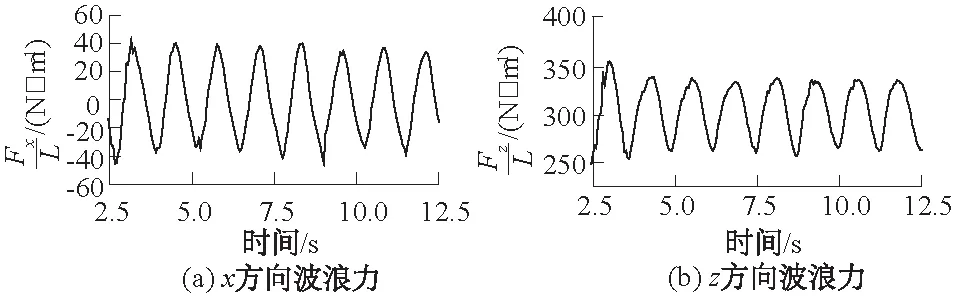
图5 S2工况下单个箱式浮体所受的波浪力Fig.5 Wave forces of a single floating rectangle box versus time in case S2
为进一步分析KC数对单个箱式浮体在波浪中的运动响应和所受波浪力的影响,图6给出了S1—S3工况下(即不同KC数条件下)浮体运动以及所受波浪力随时间的演化曲线。从图6可知,在箱体尺寸和密度保持不变的条件下,随KC数的增加,单个箱式浮体在波浪驱动下的x方向的纵向位移呈现非常明显的增加趋势,这与Chen[20]关于浮体x方向的纵向位移与波浪的波高呈正相关的研究结论相符。与之类似,z方向的垂向位移、绕y轴俯仰转动角度、x方向波浪力以及z方向波浪力均随KC数的增加而明显增大,说明KC数对单个箱式浮体的运动和所受波浪力存在一种较为明显的激励作用,KC数越大,箱式浮体运动越剧烈,相应的所受波浪力越大,浮体运动与所受波浪力之间同样呈正相关关系。
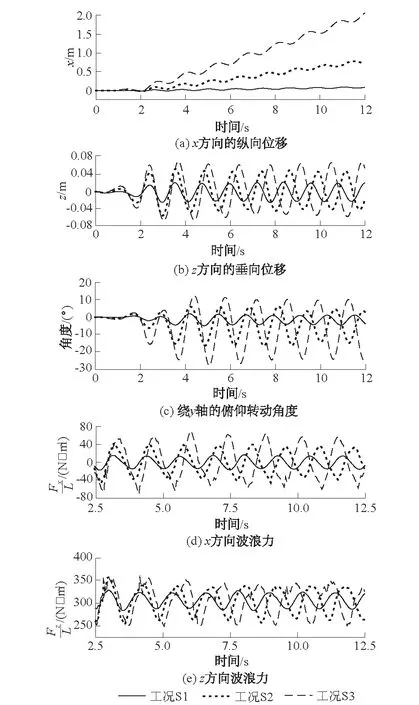
图6 S1—S3工况下单个箱式浮体运动和所受波浪力随时间变化曲线Fig.6 Motions and wave forces of a single floating rectangle box versus time in cases S1-S3
3.2 波浪驱动下2个箱式浮体的运动响应
在系统研究KC数对单个箱式浮体运动及所受波浪力影响规律的基础上,以单个箱式浮体工况为参考信息,系统分析箱体间距δ对波浪驱动下2个箱式浮体运动响应的影响。
以S2工况为参考,首先分析间距δ对浮体Ⅰ在波浪中运动响应的影响。图7给出了T1—T4工况下(即不同间距δ条件下)浮体Ⅰ运动响应随时间的演化曲线。从图7(a)可以看出,在箱体尺寸和密度保持不变的条件下,当浮体间距δ较小时(δ=1.16),浮体Ⅰ在波浪驱动下的x方向的纵向位移与S2工况有明显差距,说明浮体Ⅱ对浮体Ⅰ在x方向的纵向运动有明显的阻滞效应。而随着间距δ的增加,这种阻滞效应带来的影响逐渐减弱。当浮体间距δ较明显时(δ=3、5),浮体Ⅰ的x方向纵向位移与S2工况较为接近,浮体Ⅱ对浮体Ⅰ的阻滞效应影响较小。进一步分析图7(b)和图7(c),不同间距δ条件下浮体Ⅰ的z方向垂向位移以及绕y轴俯仰转动2个运动曲线与S2工况均较为接近,说明浮体Ⅰ在波浪驱动下的垂向运动以及俯仰转动受浮体间间距δ的影响较小。

图7 T1—T4工况下浮体Ⅰ运动响应随时间变化曲线Fig.7 Motions of floating rectangle box I versus time in cases T1-T4
图8给出了T1—T4工况下(即不同间距δ条件下)浮体Ⅱ运动响应随时间的演化曲线。从图8(a)可以看出,在箱体尺寸和密度保持不变的条件下,随着浮体间间距δ的增加,浮体Ⅱ在波浪驱动下的x方向的纵向位移呈现明显增加趋势,说明浮体之间间距较小时存在一种相互作用机制。由上文分析可知浮体Ⅰ受到浮体Ⅱ在x方向的阻滞效应,反过来浮体Ⅱ受到浮体Ⅰ在x方向的推动效应,使得浮体Ⅱ在x方向的纵向位移更为明显。随着浮体间距δ的增加,这种推动效应的影响逐渐减小。分析图8(b)可知,忽略波浪传播到浮体Ⅱ位置时间不同的客观因素,即在时间t> 4 s条件下,浮体Ⅱ在z方向垂向位移受浮体间距δ的影响较小,T1—T4工况下z方向垂向位移曲线较为接近。进一步分析图8(c),同样在忽略波浪传播到浮体Ⅱ位置时间不同的客观条件下,对比T1—T4工况中t> 4 s时浮体Ⅱ绕y轴的俯仰转动角度曲线,可以看出随着浮体之间间距δ的增加,浮体Ⅱ的俯仰转动有逐渐减弱趋势。
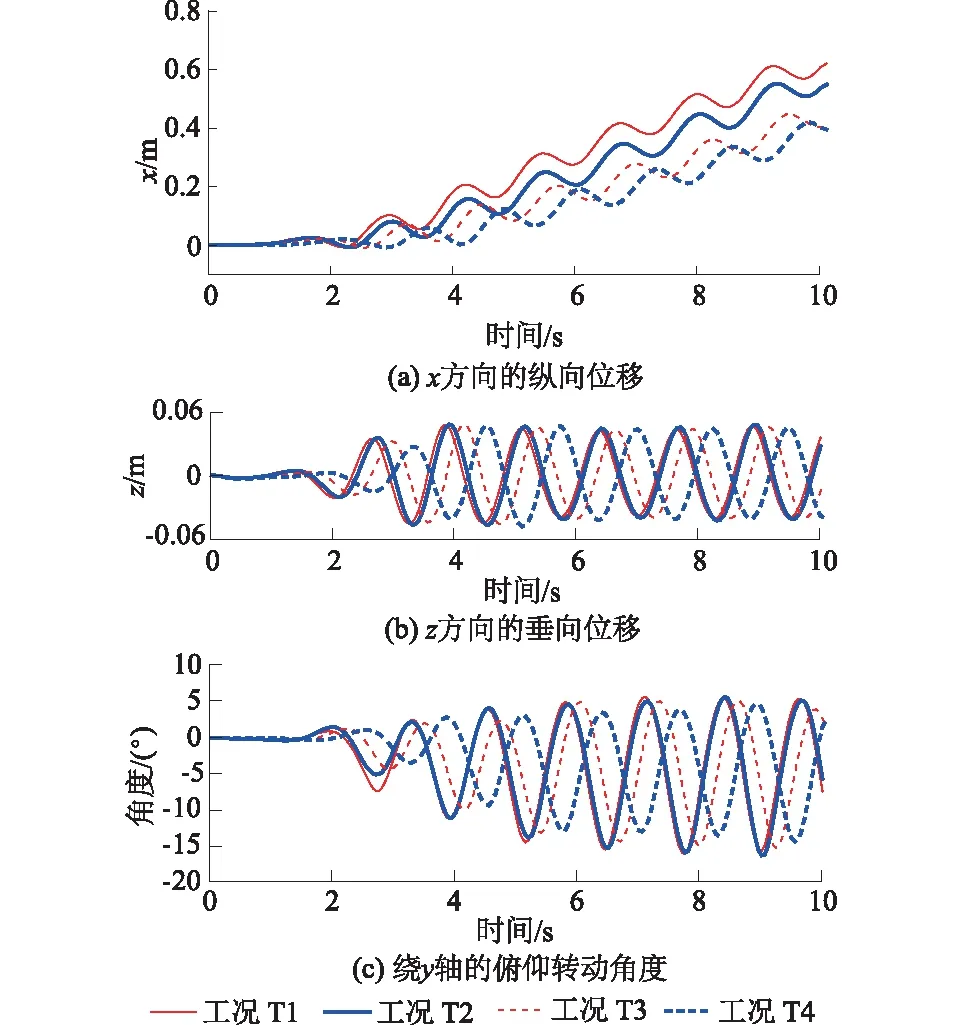
图8 T1—T4工况下浮体Ⅱ运动响应随时间变化曲线Fig.8 Motions of floating rectangle box II versus time in cases T1-T4
4 结 论
本文采用SPH方法对波浪驱动下箱式浮体的运动响应及所受波浪力进行了数值研究,具体探讨了KC数对单个箱式浮体在波浪中的运动响应及所受波浪力的影响规律,并以单个箱式浮体工况为基础进一步研究了不同间距δ对2个箱式浮体在波浪中运动响应的影响规律。所获得的主要研究结论如下:
(1)KC数对单个箱式浮体的运动和所受波浪力存在一种较为明显的激励作用,KC数越大,箱式浮体x方向的纵向运动、z方向的垂向运动以及绕y轴的俯仰转动均越剧烈,所受波浪力越大。
(2)随着浮体间距δ的增加,浮体Ⅰ在x方向的纵向位移逐渐接近于单个箱式浮体工况,而在z方向的垂向运动以及绕y轴的俯仰转动受浮体间距δ的影响较小。
(3)随着浮体间距δ的增加,浮体Ⅱ在x方向的纵向位移呈现明显的增加趋势,绕y轴的俯仰转动有逐渐减弱趋势,而在z方向的垂向运动受浮体间间距δ的影响较小。
