双浮体狭缝水动力共振的对比分析
2021-03-16何广华刘涛王威荆芃霖
何广华, 刘涛, 王威, 荆芃霖
(哈尔滨工业大学(威海) 船舶与海洋工程学院,山东 威海 264209)
随着海洋工程事业的蓬勃发展,并靠作业的多浮体系统被广泛应用于工程领域。在某些特定频率的入射波作用下,浮体间的狭缝位置会发生水动力共振现象,造成一些结构破坏及损失。因此研究2个浮体间的水动力共振问题,探究其共振机理对实际工程应用具有十分重要的意义。
国内外学者和专家对浮体间水动力共振现象进行了大量的探索与研究,采用的方法包括理论分析、试验模拟和数值计算。Miao等[1-2]使用渐近匹配法指出了双箱共振频率与箱的吃水深度及狭缝宽度存在关系。滕斌等[3-4]利用比例边界有限元方法研究了双浮体和三浮体狭缝间的共振现象。丛龙飞等[5]应用线性势流理论讨论了波浪作用下狭缝内水体共振的机理,利用特征函数展开方法对狭缝内水体波动的共振频率进行了计算与分析。Saitoh等[6]对2固定浮体间的波浪共振现象进行了物理模型试验。Iwata等[7]对3个浮体狭缝间的波浪共振问题进行了模型试验。Fredriksen等[8]利用实验的方法研究了2个运动箱体间的窄缝波高变化。Zhu等[9]数值研究了多浮体结构之间的间隙对波浪力的影响,分析了浮体间强而复杂的水动力相互作用问题。宁德志等[10-11]基于时域高阶边界元方法建立了完全非线性数值波浪水槽模型,并在窄缝内流体引入人工阻尼,研究了双浮体狭缝间的水动力特性。何广华等[12]基于约束插值剖面(constrained interpolation profile, CIP)方法,建立了二维强非线性不可压缩粘性流数值波浪水槽,研究了波浪与存在窄缝的两箱体的相互作用问题。Lu等[13]采用粘流模型和势流模型,研究了在水波作用下近距离多体间狭窄间隙内的流体共振现象。
STAR-CCM+软件在海洋工程研究领域上有着广泛的应用,它采用先进的连续介质力学数值技术,集几何建模、模型前处理、计算执行、结果后处理等功能于一体,擅长处理复杂几何,能大大缩减网格数量,计算精度较好。Zhang等[14]利用Star-CCM+开发了一个二维数值波浪池,研究了1种由浮式防波堤和振荡浮标式波浪能量转换器组成的双浮式混合系统的水动力性能。张明霞等[15]基于STAR-CCM+平台,研究了FPSO流载荷不同计算方法的适用性。Wang等[16]基于STAR-CCM+对全附件潜艇尾流场进行了数值计算,系统地分析了棱柱层网格和湍流模型对计算结果的影响。鉴于STAR-CCM+的综合优势,本文研究了2个矩形体狭缝水体共振问题。首先验证了数值建模的准确性,然后在此基础上着重研究了狭缝宽度、浮体吃水等对共振特性的影响,分析了狭缝间波高和浮体受力随入射波波数的变化规律。
1 控制方程和模型创建
1.1 控制方程
采用计算流体力学的方法研究浮体间狭缝的共振问题。考虑水的粘性,并将其视为不可压缩流体,则流体的控制方程为:
(1)
(2)
(3)

因流域包括气、液两相,采用VOF方法对自由表面进行追踪捕捉,VOF方法是根据流体体积分数的变化判断自由表面,流体相函数F为:

(4)
1.2 数值水池的建立
二维数值水池模型如图1所示,以浮体a和b的中点作为坐标的原点,波长方向为x轴,波高方向为z轴。定义浮体的宽度B=0.5 m、浮体a吃水为da,浮体b吃水为db,狭缝宽度为Bg,数值水池的水深为h=0.5 m,入射波波高H0=0.024 m。考虑入口边界到浮体a的距离至少有2个波长以及在出口边界有足够的消波区域,综合所要模拟的波长,设定模型总长15 m,高1 m。

图1 二维数值水池模型示意Fig.1 The schematic diagram of two-dimensional numerical wave tank
流域的网格划分对模拟结果十分重要,本文采用切割体网格划分流域,并对浮体周围和自由表面加密处理,消波区处采用拉伸体网格以减少整体网格数量。浮体周围网格划分如图2所示。

图2 流域网格划分示意Fig.2 Numerical mode and grid
1.3 收敛性验证
通过分析单位波长及波高内的网格数量变化来研究原点处的波高情况,如图3所示,L为波长。从图3(a)、(b)中可以看出,几种波形吻合较好,说明单位波长网格尺度Δx在L/65~L/100以及单位波高网格尺度Δz在H0/20~H0/30时,均可满足网格无关性要求。
不同时间步Δt下的波高分布情况如图4所示,从图4中可以看出,时间步Δt取值为0.003~0.005 s时,波形吻合较好,为了保证精度和效率,本文取Δt=0.004 s。
2 水动力共振结果及分析
本文对数据进行无量纲处理,将计算得到的狭缝处的波高H通过入射波波高H0进行无量纲化处理为H/H0,入射波波数k通过水深h进行无量纲化处理为kh。 将浮体所受到的水平波浪力进行无量纲化处理为Fx;垂向波浪力进行无量纲化处理为Fz:
Fx=fx/ρghH0ζ
(5)
Fz=fz/ρghH0ζ
(6)
式中:fx为浮体所受到的水平波浪力;fz为浮体所受到的垂向波浪力;水的密度ρ=997.6 kg/m3;重力加速度g=9.8 m/s2;ζ为计算域厚度。
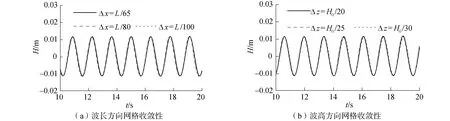
图3 网格收敛性验证Fig.3 Verification of mesh convergence
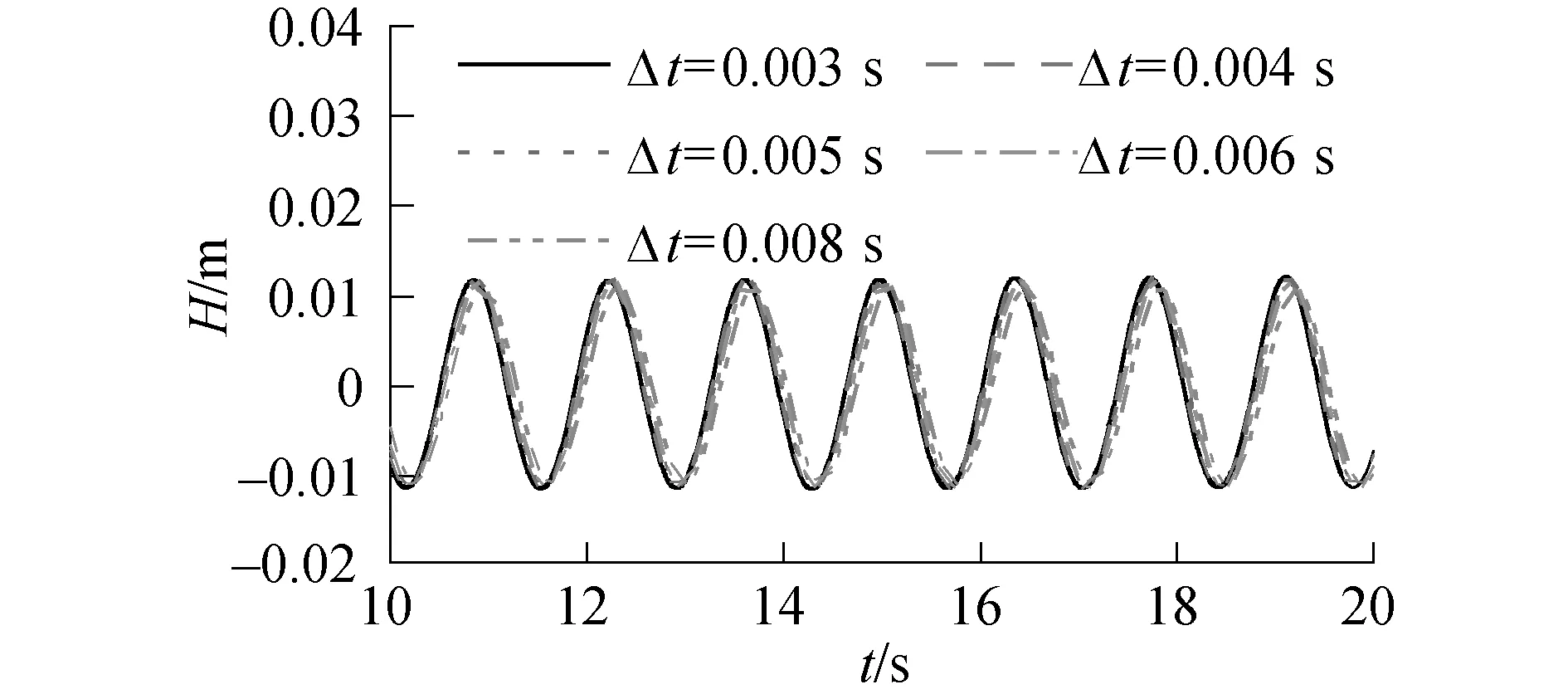
图4 时间步验证Fig.4 Verification of time step
2.1 固定双浮体狭缝水动力共振的研究
设定da=db=d=0.252 m,Bg=0.07 m。通过改变入射波波数kh,得到不同情况下的波高结果,并将其与文献[12-13]和实验结果进行对比,以验证本模型的有效性,如图5所示。
从图5可以看出,本模型所得到的共振频率为kh=1.410,相对于实验的误差为-4.016%,与文献[12-13]的结果也相差不大,均能较准确地预测共振频率。本模型得到的共振波高H/H0=4.707,相对于实验的误差为0.749%,能够较为准确地求得共振波高。从图5中可以得到:势流和粘流模型均能较为准确地预测共振频率;而势流模型由于没有考虑流体的粘性耗散,导致所求的共振波高过于偏大,说明本模型可以很好地反映狭缝水动力共振的情况。
浮体狭缝间波高的变化必将引起浮体受力的变化。图6给出的是浮体a、b所受水平和垂向波浪力随入射波波数kh变化的曲线。
从图6可以看出,在共振频率附近,势流模型由于没有考虑流体粘性的影响,导致所得的水平和垂向波浪力过大。从图6(a)、(b)可以看出,两浮体所受水平波浪力在共振频率处最大,但其系数都不超过2;浮体a所受水平波浪力在低频率处小于高频率处,而浮体b所受水平波浪力在低频率处大于高频率处。从图6(c)、(d)可以看出,浮体所受垂向波浪力在共振频率附近急剧下降,其最大垂向波浪力系数不超过1.5;浮体所受垂向波浪力在低频率处远大于高频率处;浮体a所受垂向波浪力整体上比浮体b大,浮体b在高频率入射波作用下几乎不受垂向波浪力。

图5 狭缝处的波高Fig.5 The wave height at the gap
综合图5、图6可以看出,粘流模型与势流模型相比,更能真实地反映浮体间狭缝处的水动力共振现象。
2.2 狭缝宽度对狭缝水动力共振的影响
设定da=db=d=0.252 m,计算Bg为0.03、0.05、0.07 m时的共振情况,得到共振频率及对应的波高和狭缝处波高随入射波波数的变化规律,如图7所示,得到浮体所受水平及垂向波浪力如图8所示。
从图7可以看出:在共振频率附近,狭缝处的波高先随着入射波波数kh的增大而增大,在达到最大值之后,又随着入射波波数kh的增大而减小;狭缝处波高H/H0都在4~5,说明狭缝间水体共振时狭缝处的最大波高大约为入射波波高的4~5倍;随着Bg的增加,浮体间的共振频率越小;在入射波频率kh相对较小时,狭缝宽度越大,狭缝间的波高越大,而在入射波频率kh相对较大时,狭缝宽度越大,狭缝间的波高越小。
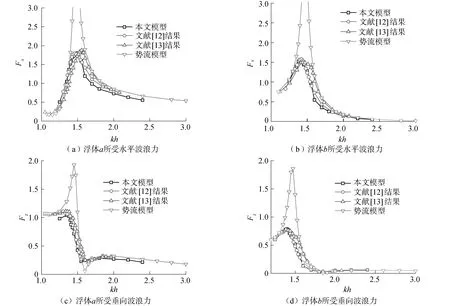
图6 浮体所受水平波浪力以及垂向波浪力Fig.6 The horizontal and vertical wave forces on floating bodies
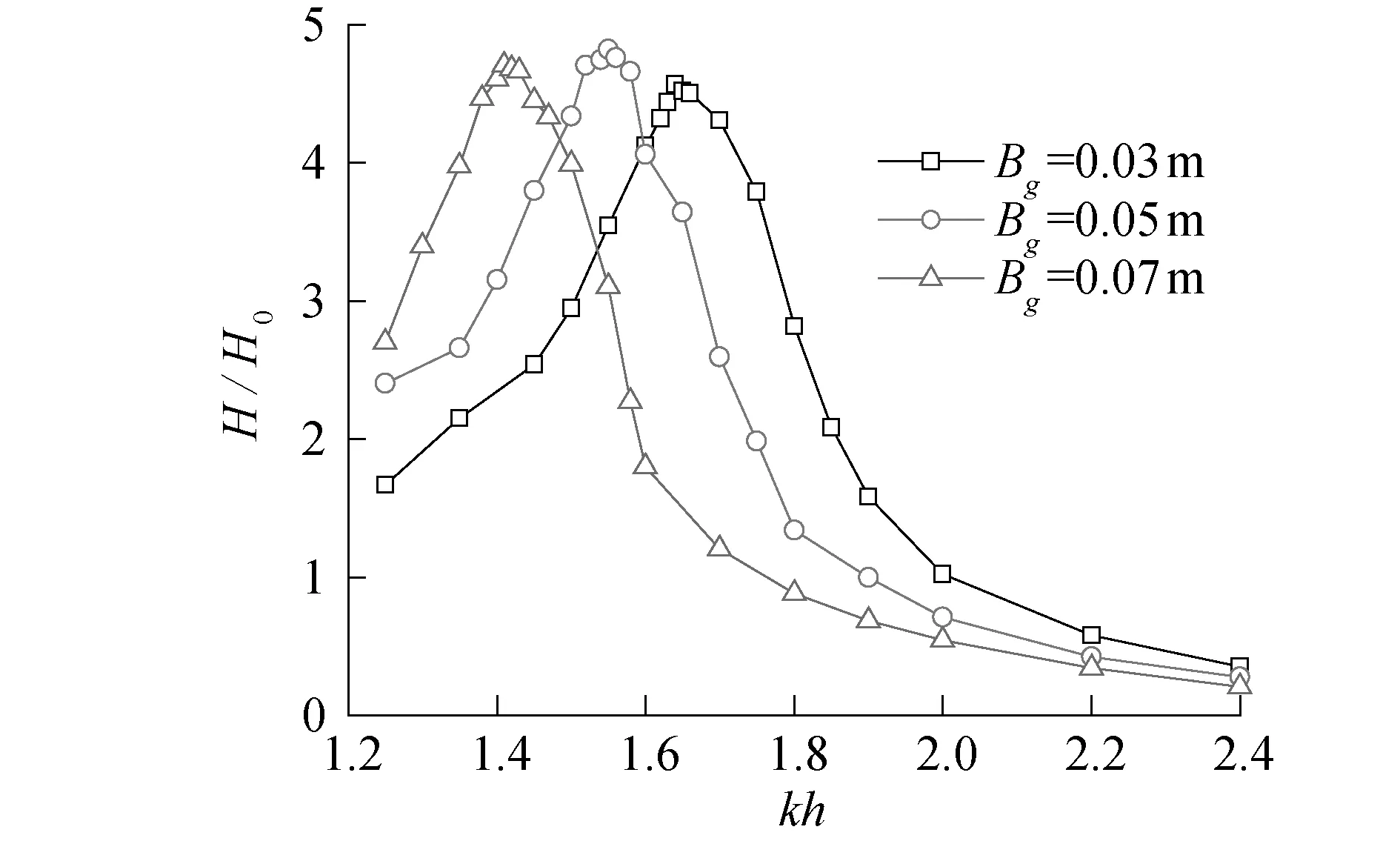
图7 不同Bg时狭缝处的波高Fig.7 The wave height at the gap under different Bg
从图8(a)、(b)可以看出:浮体受到最大水平波浪力时所对应的入射波频率随着狭缝宽度的增加而减小;浮体a所受水平波浪力在低频率处小于高频率处,而浮体b所受水平波浪力在低频率处大于高频率处;在入射波频率kh相对较小时,狭缝宽度越大,浮体所受到的水平波浪力越大,而在入射波频率kh相对较大时,狭缝宽度越大,浮体所受到的水平波浪力越小。
从图8(c)、(d)可以看出:浮体所受垂向波浪力在共振区间急剧地下降,浮体在共振频率后所受垂向波浪力的值远小于共振频率前的值;浮体所受垂向波浪力的共振区间长度随狭缝宽度的增加而减小;浮体b所受垂向波浪力整体上小于浮体a所受的波浪力;在高频率入射波作用下,狭缝宽度对浮体所受垂向波浪力的影响较小。
2.3 浮体吃水对狭缝水动力共振的影响
设定浮体狭缝间宽度Bg=0.05 m,模拟浮体吃水da=db=d为0.103、0.153、0.252 m时的共振情况,得到狭缝处波高H/H0随入射波波数kh的变化规律,如图9所示。
从图9可以看出:随着浮体吃水的增大,狭缝间共振时的频率减小,而所对应的最大波高增大。这是由于随着浮体吃水的增加,狭缝间参与共振的流体增加,流体质量的增大导致狭缝处流体的固有频率减小,所以对应的共振频率减小。而共振频率减小,导致对应的共振波长增大,从而使狭缝处流体获得的能量增加,使流体运动更加激烈,因此狭缝处的波高增大。
浮体a及浮体b所受水平波浪力Fx以及垂向波浪力Fz随入射波波数kh的变化规律,如图10所示。
从图10可以看出:浮体所受波浪力所对应的共振频率或区间随浮体吃水的增大而减小,浮体所受水平波浪力的峰值随着浮体吃水的增加而增大;浮体所受垂直波浪力在共振区间剧烈地下降,且在共振区间前所受垂向波浪力的值远大于共振区间后的值。
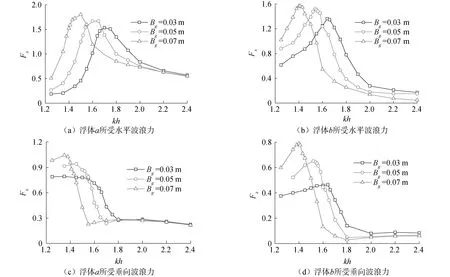
图8 不同Bg时浮体所受水平波浪力以及垂向波浪力Fig.8 The horizontal and vertical wave forces on floating bodies under different Bg

图9 不同浮体吃水下狭缝处的波高Fig.9 The wave heights at the gap with different drafts of floating body
2.4 两浮体吃水不同时的共振情况
保持狭缝宽度Bg=0.05 m等条件不变,改变浮体a、b的吃水,研究工况1:da=0.153 m、db=0.252 m以及工况2:da=0.252 m、db=0.153 m时的共振情况。通过改变不同的入射波波数kh,得到其狭缝处波高以及浮体受力的变化规律,如图11、12所示。
从图11可以看出:工况1相比于工况2,狭缝处的波高整体偏大。这是由于当da

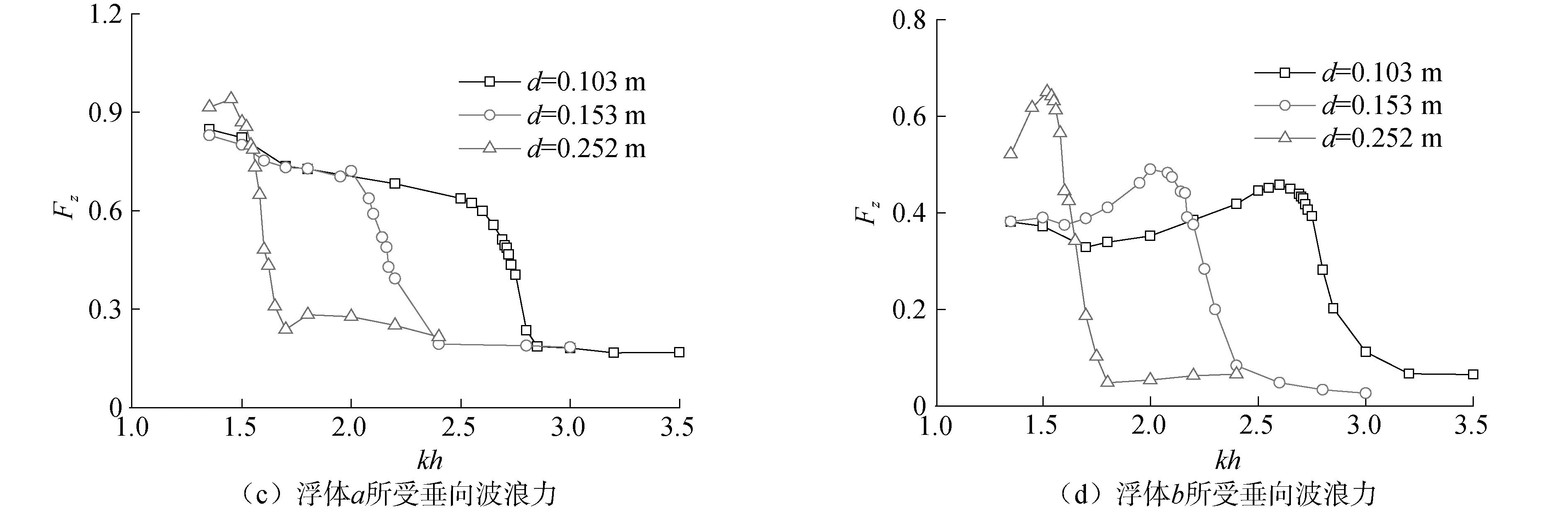
图10 不同吃水浮体所受水平波浪力以及垂向波浪力Fig.10 The horizontal and vertical wave forces on floating bodies under different d
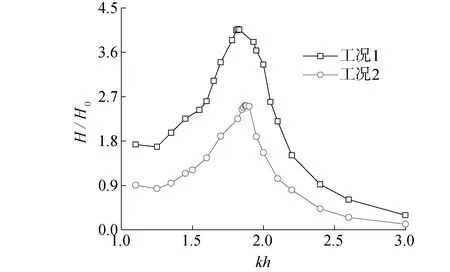
图11 不同工况下狭缝处的波高Fig.11 The wave height at the gap under different case
从图12中可以看出:2种工况下,2浮体所受水平波浪力在共振频率附近都随着kh先增大再减小,但浮体a所受水平波浪力在共振频率附近大致相同,而浮体b则明显工况1情况下大于工况2;2浮体所受垂向波浪力在2种工况下的变化规律也相同,在共振频率附近都存在一个明显的剧烈变化阶段,可以看出工况1情况下的浮体所受垂向波浪力明显偏大,这是由于浮体a、b吃水的相对关系对狭缝波浪作用的影响不同所致,且在共振频率附近两者相差较大,而在频率较大处两者相差较小;2种工况下的共振频率基本相同,浮体所受垂向波浪力在较大频率处的值明显小于较小频率。

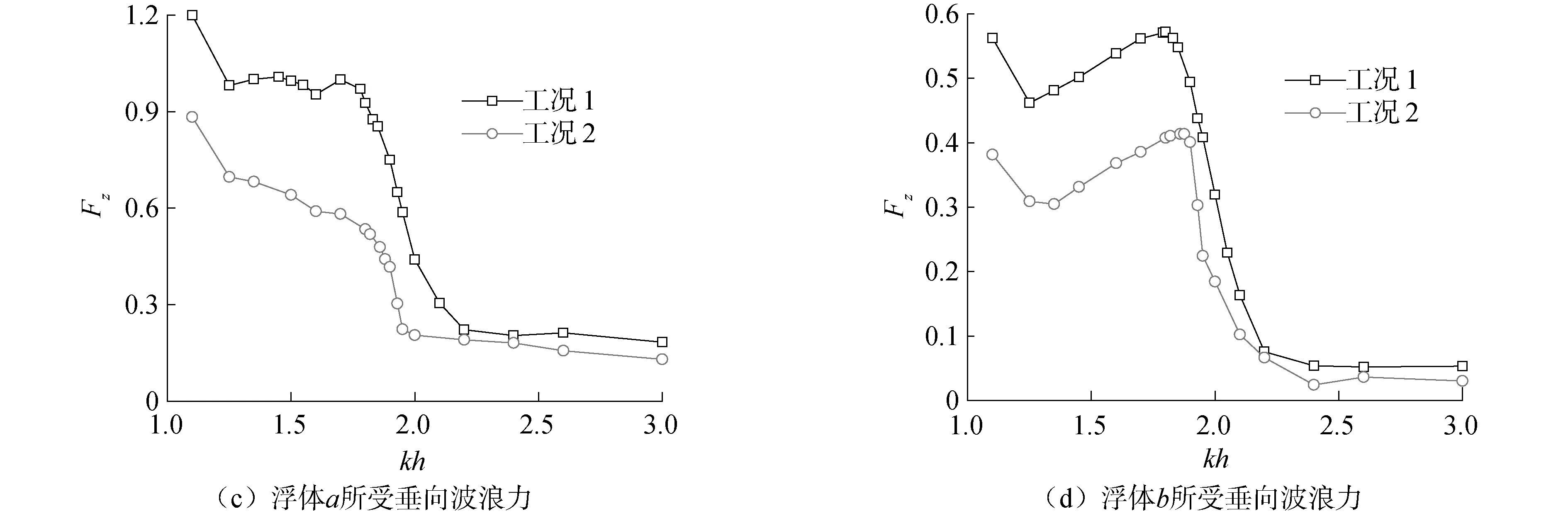
图12 不同工况下浮体所受水平波浪力以及垂向波浪力Fig.12 The horizontal and vertical wave forces on floating bodies under different case
3 结论
1)在某些特定频率入射波的作用下,浮体狭缝间会发生强烈的水动力共振现象,狭缝处的波高显著增大,浮体的受力也会增大。
2)狭缝宽度对狭缝间水动力的共振现象存在影响。狭缝宽度越大,达到最大波高时所对应的共振频率越小。
3)浮体吃水对狭缝间水动力的共振现象存在影响。当2浮体吃水相同时,浮体吃水越大,达到最大波高时所对应的共振频率越小、狭缝间的共振波高越大;当2浮体吃水不同时,迎浪侧浮体吃水越小,狭缝间的共振波高越大。
本研究对于双船并靠作业、船-泊位作业等具有十分重要的意义,在后续的研究中将深入考虑自由度的影响,使其更好地指导工程运用。
