低转速条件下的弹丸飞行稳定性分析*

吕铁钢,张亚,李世中

(中北大学 机电工程学院，山西 太原 030051)

0 引言

制导炮弹引信的试验成本较高，采用模拟试验来考核引信性能是一条可行的途径。模拟试验需要解决的关键问题是通过试验弹来模拟引信发射和出炮口一定距离内的后坐环境和离心环境。制导炮弹通常在膛内转速较低，出炮口后采用尾翼稳定，为了简化试验过程，试验弹拟采用旋转稳定的制式榴弹，此时，必须分析试验弹在低转速条件下飞行一段距离时的飞行稳定性[1]。实际飞行中的弹丸攻角δ总是不等于零的，使得空气对弹丸作用的合力既不与弹轴也不与速度矢量共线反向，所以使合力在沿速度矢量反向及垂直于速度的方向上分别产生了分量，即切向阻力与升力，同时合力对质心产生了力矩。除此以外，由于弹丸的旋转和绕赤道轴的转动等原因，又产生了极阻尼力矩、赤道阻尼力矩以及马格努斯力和马格努斯力矩等空气动力和力矩[2]，使得弹体的飞行稳定性分析变得较为复杂。弹箭的飞行稳定与弹丸的气动力外形设计密切相关，传统的设计周期长、效费比低，已不再适应现代武器的设计要求。采用数值计算方法模拟空气状态，在一定的虚温、气压、密度、黏性等条件下，计算出弹丸在外流场所受到的影响和限制。

本文首先利用Solidworks设计出弹丸的整体结构，然后运用数值计算，得出弹丸飞行稳定性的条件，通过Workbench Fluent软件仿真出弹丸外流场域所受到空气动力学的影响，进而结合数值计算分析，验证数值仿真计算对弹丸气动外形设计的可行性。

1 弹丸的结构外形设计

弹箭在空中运动时如果攻角很小，说明弹头指向飞行前方，并且弹轴与飞行方向基本一致，弹箭可以平稳地飞行，达到预期的飞行目的。如果攻角很大，则弹箭将围绕质心大幅度摆动，导致飞行极不平稳，甚至翻滚向前，与预期结果相违背，那么弹箭的飞行稳定性就显得尤为重要。根据弹丸设计的要求[3]，试验弹自行设计其内外部结构，结合数据，对试验模型进行简化处理，部位安排分为弹头部、圆柱部和弹尾部，具体结构比例如图1所示。

由于条件需要，将榴弹出炮口速度拟定为270 m/s,旋转速度30 r/s，基本数据如表1所示。假设弹体结构强度满足需要，在标准条件下，榴弹在空气中飞行将受到空气动力和力矩的作用，为使弹丸满足飞行稳定要求，需要合理设计弹丸结构，并且确定满足飞行稳定的转速。

变量数值弹重/kg23弹长/m0.688 7极转动惯量/(kg·m2 )0.042 230赤道转动惯量/(kg·m2 )0.464 528初速/(m·s-1)270

2 弹丸飞行稳定性分析

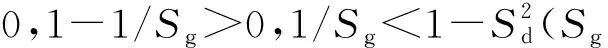
Sg=P2/4M,

(1)

Sd=(2T-H)/H,

(2)

T=by-kyA/C,

(3)

H=kzz+by-bx-gsinθ/v2,

(4)

式中:P为陀螺转速项;M为静力矩;T为马格努斯力矩;H为赤道阻尼力矩。

2.1 弹丸的急螺稳定性题

为了实现飞行稳定，弹丸应绕自身轴线进行高速旋转，以此来克服翻转力矩的不利作用。弹丸的急螺稳定性与陀螺稳定因子有关，理论上，只要使急螺稳定系数σ0>0，即可使弹丸保持稳定[6]，但是“稳定”含义是弹丸不会翻滚向前，远远满足不了射击精度的要求。弹丸的急螺稳定性直接决定着弹丸的章动，当弹丸的章动角越来越大时，说明弹丸不稳定，只有当陀螺稳定因子S>1时，弹丸才具有急螺稳定性[7]。当陀螺稳定因子

(5)

(6)

式中:σ为稳定系数;α为进动角速度;β为翻转力矩参量

对于旋转弹丸，α及β的具体值为

(7)

(8)

式中:Jx为弹丸的极转动惯量；Jy为弹丸的赤道转动惯量；ωr为弹丸的角速度。

翻转力矩

(9)

将α及β代入式(6)，可以得到

(10)

根据式(10)可以求出弹丸出炮口后一段距离内的急螺稳定性σ≈0.75>σ0=0.6，所以说此段距离内满足急螺稳定性。

2.2 弹丸的追踪稳定性

当弹丸在弹道曲线段飞行时，弹道切线的方向时刻都在改变。这时，亦要求弹丸的动力平衡轴作相应的变化，以保持二者在任意时刻都没有很大的偏差[8]。弹丸的动力平衡轴能够随着弹道切线作相应的变化，弹丸的追踪稳定性是由于空气动力矩对弹丸的作用达到的。在弹道顶点处，该处的空气动力矩小而弹道曲率大，故其追随稳定性差[9]。

(11)

当射角θ=45°时，根据外弹道方程可以求出曲线顶点坐标(3 719.39,1 859.69)，利用抛物线弹道的特点

(12)

(13)

(14)

根据空气密度函数H(y)=P/R1τ，

(15)

根据式(11)得出动力平衡角δps约等于0.042°，小于[δ]=(0.09°～0.12°)，由此可以判断出，在出炮口大约200～300 m，弹丸满足追随稳定性。

3 外流场仿真分析

3.1 模型建立与网格生成

用Solidworks三维建模软件设计出122 mm榴弹模型，由于是对弹丸外流场仿真[10]，故简化其内部结构，根据一定比例建立模型。用Workbench Fluent导入模型后先建立弹体的外部绕流，仿真模型长度为5.645d(d为榴弹直径)，为减小流场域边界对仿真分析的影响，保证结果的准确性，建立一个外部直径为20d，长40d的流场域，再以ANSYS ICEM CFD生成非结构网格，检查生成网格的质量，模型与网格分别如图3，4所示。

3.2 流体力学分析

当弹体在空气中飞行时，会受到地心引力和空气动力的作用，忽略地球绕太阳公转的影响，弹体由于受到重力以及其他外力的因素，飞行稳定会受到干扰，由于空气的移动，弹体飞行过程中将受到空气动力和力矩的作用[11]，其中空气动力矩使弹体产生绕质心的转动并进一步改变空气动力，从而影响质心的运动，这种转动会对弹体的稳定性造成一定的影响。对于所有流动，都需要满足质量和动量守恒方程，对于包含传热或可压性流动，还需要满足能量守恒方程[12]。

3.3 初始条件和边界条件

进行设置操作环境和边界条件，选择三维求解器，定义可压缩空气与压力远场的边界条件，假设来流为理想气体，粘度满足萨兰德定理，继而进行榴弹的外部绕流分析，来流攻角α=0°～10°，来流马赫数为Ma=0.8，通过计算机模拟获得榴弹在特定条件下有关信息[13]。

3.4 求解过程

选择求解的方程类型为Ros-FDS通量差分法[14]，在微分离散格式中，梯度采用基于单元的最小二乘法，在Fluent中默认的收敛准则为所监视的残差值、绝对值均小于0.001，迭代3 000步，图形窗口中会动态显示阻力系数图5、升力系数图6随迭代过程的变化曲线，以及残差图随迭代过程的变化曲线，如图7，求解后对计算结果进行后处理，即可以得到绕榴弹的流线图和榴弹表面的压力分布云图如图8所示。

4 仿真结果分析

攻角/(°) 转速/(rad·s-1) 21 755.8841 789.9061 822.9681 854.96101 885.80

5 结束语

根据上述数值计算分析，得出弹丸在出炮口速度为270 m/s，旋转速度30 r/s时，在空气中飞行曲线中不具有飞行稳定性，但是在距离出炮口200～300 m，飞行稳定性不受影响，可以作为考核引信性能载体。通过仿真分析，得出试验弹设计合理。由此可以发现弹丸在空气中的飞行稳定性与出炮口速度以及旋转速度有关，为保持弹丸的飞行稳定，必须合理设计弹体结构以及发射药量的多少。

参考文献：

[1] 王超伦,薛林.导弹气动性能对弹体响应特性影响分析[J].现代防御技术,2016,44(6):174-180.

WANG Chao-lun,XUE Lin.Analysis of Response Characteristic Influence upon Missile Aerodynamic Performance[J].Modern Defence Technology, 2016,44(6):174-180.

[2] 彭勇,习滔滔.122 mm火箭弹制导化发展途径研究[J].现代防御技术,2016,44(3):18-24.

PENG Yong,XI Tao-tao.Guidance Development of 122 mm Rocket[J].Modern Defence Technology,2016,44(3):18-24.

[3] 贾子英,陈松辉,叶春燚.作战体系结构稳定性突变分析[J].现代防御技术,2016,44(1):1-4,21.

JIA Zi-ying,CHEN Song-hui,YE Chun-yan.Analysis of Stability of Operation SoS Structure Based on Catastrophe[J].Modern Defence Technology,2016,44(1):1-4,21.

[4] 祁载康.制导弹药技术[M].北京：北京理工大学出版社,2002.

QI Zai-kang.Guided Ammunition Technology[M].Beijing:Beijing Institute of Technology Press,2002.

[5] 钱翼稷.空气动力学[M].北京：北京航空航天大学出版社,2004.

QIAN Yi-ji.Aerodynamics[M].Beijing:Beijing University of Aeronautics and Astronautics Press,2004.

[6] 谷逸宇.多导弹编队飞行导引律设计[J].现代防御技术,2014,42(1):51-55.

GU Yi-yu.Guidance Law of Multi-Missiles Formation Fight[J].Modern Defence Technology,2014,42(1):51-55.

[7] 美军装备司令部.弹丸的飞行稳定性设计[M].杨为中,译.北京：国防工业出版社,1976.

The United States Military Equipment Command.The Flight Stability Design of Projectiles[M].YANG Wei-zhong，Translatied.Beijing:National Defense Industry Press,1976.

[8] 韩子鹏.弹箭外弹道学[M].北京：北京理工大学出版社,2014.

HAN Zi-peng.Missile Exterior Ballistics[M].Beijing:Beijing Institute of Technology Press,2014.

[9] 宋丕极.弹丸动稳定性的物理解释[J].兵工学报,1987,31(2):72-75.

SONG Pi-ji.Physical Explanation of Dynamic Stability of Projectile[J].Acta Armamentarii,1987,31(2):72-75.

[10] 王晓兵,李菁,廖忠全,等.基于FLUENT的弹丸外流场数值仿真[J].计算机辅助工程,2010,19(1):92-94.

WANG Xiao-bing,LI Jing,LIAO Zhong-quan,et al.Numerical Simulation on Outer Flow Field of Projectile Based on FLUENT[J].Computer Aided Engineering,2010,19(1):92-94.

[11] 姜波,齐杏林,贾波,等.基于fluent的弹丸外流场仿真计算[J].计算机仿真,2014,31(3):38-40,45.

JIANG Bo,QI Xing-lin,JIA Bo,et al.Simulation Research on Projectile External Flow with Fluent[J].Computer Simulation,2014,31(3):38-40,45.

[12] 伍星,卢永刚,宋琼,等.基于Fluent的弹体气动特性计算与分析[J].兵器装备工程学报,2016,37(2):22-25.

WU Xing,LU Yong-gang,SONG Qiong,et al.Fluent-Based Calculation and Analysis of Missile Aerodynamic Characteristics[J].Journal of Ordnance Equipment Engineering,2016,37(2):22-25.

[13] 王朋飞,曹红松,王智军,等.高旋火箭弹增程稳定性设计及气动特性分析[J].弹箭与制导学报,2012,32(5):124-126.

WANG Peng-fei,CAO Hong-song,WANG Zhi-jun,et al.Stability Design and Aerodynamic Characteristics Analysis of High Rotating Rocket Projectile[J].Journal of Projectiles,Rockets,Missiles and Guidance,2012,32(5):124-126.

[14] 周觐,雷虎民,李炯,等.导弹俯仰通道制导控制一体化设计[J].现代防御技术,2014,42(5):80-84,90.

ZHOU Jin,LEI Hu-min,LI Jiong,et al.Integrated Design of Guidance and Control for Missile Pitching channel [J].Modern Defence Technology,2014,42(5):80-84,90.

[15] 范文锋,许波,郝昀.助推-滑翔飞行器弹道最优控制研究[J].现代防御技术,2014,42(3):31-36.

FAN Wen-feng,XU Bo,HAO Jun.Trajectory Optimal Control for Boost-Glide Vehicle[J].Modern Defence Technology,2014,42(3):31-36.

[16] 江晓东,谢京稳,郭军海.基于动力学模型的弹道式再入弹道估计方法[J].现代防御技术,2014,42(2):128-133.

JIANG Xiao-dong,XIE Jing-wen,GUO Jun-hai.Ballistic Reentry Trajectory Estimation Method Based on Dynamic Model[J].Modern Defence Technology,2014,42(2):128-133.