集成时频特征的拖曳式诱饵存在性检测方法*

陈安娜

(中国空空导弹研究院，河南 洛阳 471009)

0 引言

拖曳式雷达诱饵是一种新型的角度欺骗干扰技术，可有效破坏雷达系统对目标的搜索、截获与跟踪，已成为雷达的有效干扰手段之一[1-2]。目标回波与诱饵干扰信号相互干涉混叠，导致常规单脉冲测角不再可靠[3]。雷达系统无法准确地检测波束内拖曳式诱饵干扰的存在对于实现目标的稳定跟踪是十分致命的[4]。

目前针对诱饵的检测大多基于多普勒特征，即利用诱饵释放导致的回波频谱展宽来判定干扰存在[5]。实际中雷达、目标和诱饵均处于剧烈的相对运动之中，目标和诱饵的多普勒频率特征是时变且非平稳的。传统傅里叶变换只能描述信号的频率成分，不能反映频率分量随时间的变化特性，容易引起频谱展宽，致使基于多普勒谱线展宽的检测判决方法在使用上具有很大的局限性。信号的时间-频率联合分布能够展现频谱分量随着时间的变化情况，提供单独用时间分析或频率分析所不能描述的信号特性[6-7]。因此，可以利用时频分析方法描述干扰发生前后接收回波时频域特性的变化，从而揭示回波信号成分的改变，以此来判定诱饵干扰的存在性。本文在对拖曳式诱饵干扰特点以及时频特性进行详细分析的基础上，采用WVD+Hough变换来检测接收回波中多分量信号的存在性，然后通过设计阈值门限进行判决，实现了干扰的准确检测。

1 干扰条件下的回波时频特性

图1给出了迎头攻击态势下导弹、目标和诱饵的三角几何关系图[8-9]。

诱饵与目标速度大小为vT，方向与水平线的夹角为β；导弹飞行速度vM，与水平线的夹角为φ，与目诱质心的距离为R；雷达波束中心指向与水平线的夹角为θ，且有θ∈(0,π/2)。θ1和θ2分别为雷达目标连线、雷达诱饵连线与水平线的夹角，Ω为目标和诱饵相对于雷达天线的张角。w为雷达波束中心指向与导弹航向之间的夹角，w=φ-θ且w∈[0,π/4]。图1中目标与诱饵的质心位置由诱饵和目标回波功率的大小关系来决定[10]，设诱饵干扰与目标回波功率的比值为k(称作干扰压制比)，则导引头雷达波束中心指向相对于目标与诱饵几何中心线的偏离角为[11]

(1)

设在一个相参处理周期T内，vT，vM和φ均保持不变，则目标与诱饵的多普勒频差可分别表示为

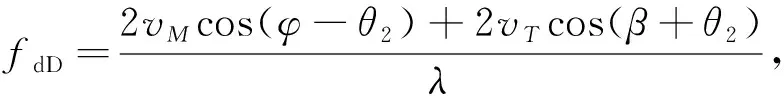
(2)

将式(2)中的多普勒频差项进行因式分解可得

(3)

由于Ω较小(一般不超过半功率波束宽度)，则近似有sinΩ≈Ω和(θ1+θ2)/2≈θ成立，设目标与诱饵之间拖曳线的长度为L，则Ω可近似为Ω≈Lsinθ/R，则式(3)可进一步化简为

(4)

上面从静止几何关系角度分析了目标和诱饵的多普勒频率及其频差的变化规律。在实际攻击过程中，需要结合实际干扰条件下的动态制导过程才能准确获得回波多普勒的时变特性[12]。

假设弹目初始距离为10 km，诱饵在目标的拖曳下在方位维进行机动，俯仰维保持初始角度不变。0时刻目标开始释放诱饵，面向导弹匀速直线飞行，1 s后目标向右侧机动形成三角态势。当导弹的初始攻击前置角在[-20°～20°]变化时，可得目标和诱饵的多普勒频率以及二者多普勒频差的变化曲线如图2所示。

图2表明，迎头态势下目标和诱饵的多普勒频率具有时变性，其变化趋势近似满足线性调频模型；诱饵释放初期，目标与诱饵的多普勒频差较小，随着目标机动和三角态势的形成，二者的多普勒频差逐渐增大。该特性在尾追态势下同样适用。因此，可以分别用单分量线性调频模型和多分量线性调频模型来描述干扰释放前后导引头接收的回波，且目标与诱饵在时频面的显现特征差异逐渐增大，有利于特征差异的提取和干扰的检测判定。

2 WHT变换与特征差异提取

Wigner-Ville 分布( WVD)可视为信号能量在时频域的二维分布，作为一种典型的双线性时频描述方法，具有较好的分辨率，非常适合处理线性调频非平稳信号[13]。

根据线性调频模型近似，拖曳式诱饵干扰下的导引头接收回波可等价表示为

(5)

式中:M=2表示接收回波中同时包含目标和干扰2部分信号分量。

对混合接收回波进行WVD变换可得

(6)

可以看出，多个线性调频信号表现为自项分量所对应的多条斜率为μm，初始频率为ωm的实线，以及各交叉分量对应的虚线。

各分量之间的交叉项使得时频面内模糊不清，信噪比不高情况下甚至难以发现各个线性调频(LFM)分量。目前许多研究提出了抑制交叉项的方法，如设计核函数有选择的取舍模糊函数中的各部分能量，保留自项分量的同时抑制交叉项等[14]。然而核函数设计复杂，计算量大，抑制效果因信号模型差异而不稳定，可推广性不强。干扰存在性检测只需要判定回波时频处理后所包含的信号分量个数，不需要获得各分量对应的精确参数，因此并不需要将交叉项完全抑制。

交叉项的能量比自项分量的能量小很多，且呈现振荡型。Hough变换可将被检测图像的参数曲线在参数空间聚集起来形成与曲线对应的参数峰值点[15]。将WVD分布结果变换到Hough平面，可以使得自项分量在Hough平面呈现多个尖峰，而交叉项因振荡而散布得比较开，二者易于区分。因此，可以利用Hough变换将时频分析结果映射到相关参数平面，通过对平面内峰值数目的检测来实现干扰的存在性判决。在WVD分析的基础上进行Hough变换，称之为Wigner-Hough变换，简称WHT。

混合接收回波x(t)的WHT结果可表示为

(7)

回波中的不同线性调频分量经过WHT变换后将在参数平面内呈现不同的尖峰，但是在信噪比较低的情况下，交叉项和噪声的起伏比较快，可能导致对应WHTx(ρ,θ)中某个θ切片出现伪峰，引起峰值误判。通过对回波的WHT变换进行自适应滤波平滑处理，可有效降低虚警概率。自适应滤波权重可定义为

(8)

图3为双分量线性调频回波的自适应平滑WHT处理结果。

可以看到，WHT变换使得线性调频自项分量在参数平面呈现尖峰特性，同时在一定程度上有效抑制了交叉项，能够有效分离不同的信号分量。因此，通过检测干扰释放前后峰值特征的差异即可实现干扰的存在性检测判决

3 序贯干扰存在性检测器设计

干扰检测判决需要设置合理的阈值门限。阈值上限需小于干扰释放前目标回波信号对应的峰值，阈值下限需大于交叉项和噪声项引起的伪峰。通过对参数平面峰值进行过门限检测，根据判定的尖峰数目即可确定干扰的存在性。

考虑到单次判决可能存在虚警，采用序贯累积判决的方式对单次判决结果进行确认，流程如图4所示。其中，利用干扰释放时导引头回波功率陡增引起的自适应增益控制AGC跳变作为指示信号，实现阈值门限计算和门限判决切换。

图4中：λL为检测门限。检测量Λ的数学意义为：取L=5，若λL=0.4，则表示连续5次检测中至少要2次检测到诱饵才能判决其存在性；若λL=0.6，则表示连续5次检测中至少要3次检测到诱饵才能判决其存在。

4 仿真实验及分析

仿真场景设置与图2一致，考虑到对阈值门限计算的评估，将诱饵释放时间从0时刻后移至第1 s时刻，即目标从0时刻到第1 s之间面向导弹匀速直线飞行，在第1 s时释放诱饵，同时进行机动飞行以形成干扰三角态势，在诱饵释放的同时模拟AGC跳变指示。单次仿真情况下不同攻击时刻的MHT处理结果如图5所示。

图5表明，干扰释放前只有目标回波对应的一个尖峰；诱饵释放初期，目标和诱饵的多普勒相差不大，并且干扰功率远大于目标回波功率，目标回波的峰值被干扰信号的峰值所覆盖，两者高度重合；随着三角态势的形成，目标与诱饵的多普勒差异增大，WHT参数平面内的目标和干扰对应尖峰分离程度越来越高。

5 结束语

拖曳式诱饵干扰条件下导引头雷达接收回波中目标和诱饵的多普勒变化可以用线性调频模型来近似。本文通过分析诱饵干扰特点以及时频变化特性，采用自适应平滑WHT对接收回波进行处理，通过检测目标和干扰信号在WHT参数平面内的信号峰值进行干扰的存在性判决。干扰动态实验结果表明，基于时频特征的干扰存在性检测方法能够准确检测干扰的发生。

参考文献：

[1] William J Kerins.Analysis of Towed Decoy[J].IEEE Transactions on Aerospace and Electronic Systems,1993,29(4):1222-1227.

[2] 张文俊.新一代先进诱饵发挥出巨大作用[J]．电子侦察干扰，2001,3(2)：39-42．

ZHANG Wen-jun.The New Generation Decoys Bring Great Effect [J].Electronic Reconnaissance and Jamming,2001,3(2)：39-42．

[3] 肖钦定,刘晓东,李海林.机载拖曳式诱饵角度欺骗干扰分析[J].航天电子对抗,2011(4):13-16.

XIAO Qin-ding,LIU Xiao-dong,LI Hai-lin.Angle Deception Jamming Analysis of Airborne Towed Decoy[J].Aerospace Electronic Warfare,2011(4):13-16.

[4] 宋志勇,肖怀铁.基于角闪烁效应的拖曳式诱饵存在性检测[J].信号处理,2011,27(4):522-528.

SONG Zhi-yong,XIAO Huai-tie.Detection of Presence of Towed Radar Active Decoys Based on Angle Glint[J].Signal Processing,2011,27(4):522-528.

[5] 廖云,何松华,张军.脉冲多普勒雷达抗拖曳式干扰方法研究[J].雷达科学与技术,2009，7(5):325-328.

LIAO Yun,HE Song-hua,ZHANG Jun.Method Research on Monopulse Doppler Radar Countering Towed Decoy Jamming[J].Radar Science and Technology,2009,7(5):325-328.

[6] 李秀梅,杨国青.几种时频分析方法的性能比较[J].计算机仿真,2015,32(3):220-224.

Li Xiu-mei,YANG Guo-qing.Performance Comparisons Among Time-Frequency Representations[J].Computer Simulation,2015,32(3):220-224.

[7] Peter Balazs,Monika Doerfler,Matthieu Kowalski,et al.Adapted and Adaptive Linear Time-Frequency Representations a Synthesis Point of View[J].IEEE Signal Processing Magazine Special Issue on Time-Frequency Analysis and Applications,2013,30(6):20-31.

[8] 白渭雄,焦光龙,付卫红.拖曳式诱饵对抗技术研究[J].系统工程与电子技术,2009,31(3):579-582.

BAI Wei-xiong,JIAO Guang-long,FU Wei-hong.Study on Antagonistic Technology of Towed Decoys[J].System Engineering and Electronics,2009,31(3):579-582.

[9] 张兴利,梁燕青,王建.雷达型导弹抗拖曳式诱饵干扰半实物仿真试验技术[J].航空兵器,2015(6):55-57.

ZHANG Xing-li,LIANG Yan-qing,WANG Jian.HWIL Simulation Technology of Anti-Towed Decoy Interference for Radar Missile[J].Aero Weaponry,2015(6):55-57.

[10] 夏中楠,方群.主动雷达抗拖曳式诱饵干扰的角度提取方法[J].航空兵器,2009(5):26-28.

XIAN Zhong-nan,FANG Qun.Acquiring Method of Angle for Active Radar Against TRAD[J].Aero Weaponry,2009(5):26-28.

[11] SONG Zhi-yong,XIAO Huai-tie,ZHU Yi-long,et al.A Novel Approach to Detect the Unresolved Towed Decoy in Terminal Guidance[J].Chinese Journal of Electronics,2012,21(2):367-373.

[12] 林鹏,刘亚枫,马东立,等.航空拖曳式诱饵的释放过程研究[J].飞机设计,2015,35(1):1-5.

LIN Peng,LIU Ya-feng,MA Dong-li,et al.Study of Release Process of the Aeronautic Towed Decoy[J].Aircraft Design,2015,35(1):1-5.

[13] Merlin Thomas,Roshen Jacob,Lethakumary B.Comparison of WVD Based Time-Frequency Distributions[C]∥Proceedings of the International Conference on Power,Signals,Controls and Computation.Thrissur:IEEE Press,2012:331-342.

[14] Milos Dakovic,Thayananthan Thayaparan,Ljubisa Stankovic.Time-Frequency-Based Detection of Fast Maneuvering Targets[J].IET Signal Processing,2010,4(3):287-297.

[15] 王泽众,刘锋,黄宇,等.离散周期Wigner-Hough变换及其检测性能分析[J].电讯技术,2012,52(9):1452-1458.

WANG Ze-zhong,LIU Feng,HUANG Yu,et al.Digitized Periodic Wigner-Hough Transform and Its Performance Analysis[J].Telecommunication Engineering,2012,52(9):1452-1458.