第三方引导下的极区超视距目标指示方法*

孙永侃,张萍萍

(海军大连舰艇学院，辽宁 大连 116018)

0 引言

超视距目标指示是战场态势感知的重要依据，是实施超视距导弹攻击的基本前提，是作战资源管理的重要依据，对提高作战效能和生存能力具有极为重要的现实意义[1-2]。超视距目标信息的指示流程为：第三方探测兵力对指定海空域进行目标搜索与探测，检测到目标后，超视距探测兵力将批号、方位、距离和速度、航向等目标数据及探测兵力自身位置信息实时传送给本舰。本舰接收到对接收到的信息进行滤波融合等数据处理，转换成可直接使用的目标数据，提供给雷达、武器系统以及指挥员进行目标指示[3-5]。特殊的地理环境使极区超视距目标跟踪的重要性提升，但超视距目标跟踪中的目标参数表示方法不能适应极区超视距目标指示的高精度需求，相关文献对提高超视距目标指示精度提出各自的看法与解决方法[6-10]，但这些研究没有考虑极区特殊的地理环境对超视距目标指示的影响，没有考虑传统超视距目标指示方法在极区的使用缺陷，因此要满足极区舰艇作战指挥需求，必须寻求合适的解决方法来提高极区超视距目标指示精度。

1 构建横向地球坐标系与横向地理坐标系

传统地理位置的表示采用经纬度方式[11]，由于极区经线收敛导致地理北迅速收敛于北极点，进而导致目标方位角的误差增大，本文提出改变传统经纬网格的定义，提出将地球球面以另外一种方式进行划分，将地球极区转变为虚拟赤道地区，从而将极区运动状态参数解算问题转化为虚拟赤道地区的运动状态参数解算问题。

依据这一假设，本文提出在虚拟的经纬网格中，将虚拟极点定义为地理赤道上某点，将虚拟赤道定义为穿过地理极点的大圆，然后依据虚拟赤道和虚拟极点设置虚拟纬线和虚拟经线，虚拟经线为收敛于虚拟极点的大圆，虚拟纬线平行于虚拟赤道面，本文将虚拟的经纬网格称为横向经纬网格，横向经纬网格中的经度称为横向经度，横向经纬网格中的纬度称为横向纬度，采用横向经纬度对地理位置进行表示。

依据上述思路，在以横向经纬网格对地球球面上的某点进行位置表示时，为了使传统经纬网格与横向经纬网格之间的转换关系尽量简便，在横向经纬网格中，定义横向北极点位于东经90°，纬度为0°的赤道处，横向南极点位于西经90°，纬度为0°的赤道处，定义横向赤道位于0°经线和180°经线上，定义横向本初子午线为经过北极点的90°E/90°W子午线。如图1所示。

为了将地理位置用横向经纬度表示，为了将横向地理北作为方位参考，本文提出在建立横向经纬网格的基础上建立横向地球坐标系与横向地理坐标系。

1.1 横向地球坐标系的建立

在横向地球坐标系中，原点仍定义为地球坐标系中的原点地球质心Oe，横向赤道面为OexTeyTe，横向本初子午面OexTezTe。横向地球坐标系如图2所示，在横向地球坐标系中，球面任意一点M点的位置用横向经纬度坐标来描述，即横向经度λT和横向纬度φT，其中：横向经度λT为横向本初子午面与通过M点的横向子午面之间的夹角，横向纬度φT为M点和地球质心连线与横向赤道面之间的夹角。

1.2 横向地理坐标系的建立

下面依据横向地球坐标系Oexeyeze建立相应的横向地理坐标系OtxTtyTtzTt，首先对坐标系作如下定义：设地球坐标系为e系；横向地球坐标系为Te系；地理坐标系为t系；横向地理坐标系为Tt系；纬度为φ；经度为λ；横向纬度为φT；横向经度为λT；地球半径为R(假设地球为球体)。横向地理坐标系的原点与地理坐标系中的原点为同一点，yTt轴指向沿当地横向经线指向横向北极点的横向北，zTt轴沿地理垂线指向上，xTt轴的方向在当地水平面内沿当地横向纬线的切线方向指向横向东，这样就建立了横向东-北-天坐标系，如图2所示。

2 构建基于横向地球坐标系的大地主题解算模型

超视距目标指示不是通常意义的视距内或平面上的距离方位，而是需要特殊转换的、地球表面的大圆弧长和方位角，通常采用大地主题解算模型进行转换。因此为了实现大地极坐标转换到横向地球坐标系的变换，本文基于横向地球坐标系建立大地主题解算公式，对横向地球大地主题解算的正解与反解公式进行求解，从而将传感器测量的目标的大地弧长距离以及方位角转化为目标的横向经纬度。同时由于在极区(特别是近极点地区)地理北不易作为方位基准，本文提出将位置坐标用横向地球坐标表示，将横向地理北作为方位基准，将目标方位用横向方位角 (即目标方位线与横向地理北的夹角)来表示，对应的大地主题解算为横向地球大地主题解算。

对于将地球近似成圆球体，横向地球大地主题解算问题就变成了求解球体上横极球面三角形(即地球横向北极点与2个大地点组成的三角形) 的问题。如图3所示。

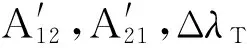
(1)

(2)

sinφT1cosφT2cos ΔλT,

(3)

cosφT1sinφT2cos ΔλT,

(4)

cosS12= sinφT1sinφT2+

cosφT1cosφT2cos ΔλT,

(5)

cosφT2cos ΔλT= cosφT1cosS12-

(6)

(7)

(8)

(9)

Δλ=λT2-λT1.

(10)

2.1 构建横向地球大地主题解算正解模型

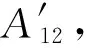
首先按式(9)求出sinφT2，再用下式求取φT2：

(11)

在求取λT2时,可先求出横向经差，ΔλT取式(1)除以式(6)就可以得到

(12)

(13)

2.2 构建横向地球大地主题解算反解模型

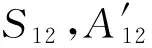
(14)

(15)

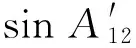
(16)

式中：p=sin ΔλTcosφT2;q=cosφT1sinφT2-sinφT1·cosφT2cos ΔλT。

3 构建基于横向地球坐标系的目标运动模型与目标观测模型

3.1 构建基于横向地球坐标系的极区超视距目标运动模型

对于舰艇类大质量动目标的机动跟踪的基础是对匀速直线运动方式和匀速慢转弯运动机动方式的跟踪[12]，因此本文使用CT模型来描述目标运动。

假设采样时间间隔为T, 令k时刻横向地球坐标系下的目标状态向量为

Xk=(λT,φT,v,ψT,ω)T

，

式中：λT，φT为k时刻目标的横向经度和横向纬度;ν为k时刻目标运动速度;ψT为k时刻目标运动的横向航向角;ω为k时刻目标运动角速度。

则横向地球坐标系下的目标运动方程如下

X(k+1)=f(X(k),k)+W(k),

(17)

式中：W(k)为均值为0、协方差为Q(k)的高斯噪声序列；f(X(k),k)为

(18)

式中:r为地球半径。

3.2 第三方引导信息进行目标观测情况下的目标观测模型建立

通过数据链进行第三方引导信息的远程目标指示与跟踪。数据链目标指示的内容有2种情况：

(1) 第三方仅提供包括经度和纬度的目标位置信息，但不提供目标运动参数。

(2) 第三方既提供包括经度和纬度的目标位置信息，也提供包括航向和航速的目标运动信息。

下面对这2种情况分别进行研究。

3.2.1 第三方仅提供目标位置参数情况下的目标观测模型构建

由于第三方仅能提供目标位置参数经度纬度，因此观测向量为

Z[k]=(λ,φ)T.

(19)

观测方程为

Z[k]=h(k,X(k))+V[k],

(20)

式中：h(k)为均值为0、协方差为R(k)的高斯噪声序列。

则观测向量Z[k]与状态向量X[k]的函数关系h(X(k),k)可以通过横向经纬度与经纬度之间的变换得到如下：

(21)

3.2.2 第三方提供目标位置及运动参数情况下的目标观测模型构建

由于第三方可提供目标的经纬度、速度以及航向信息，则观测向量可设置为

Z[k]=(λ,φv,ψ)T.

(22)

则观测量Z[k]与状态向量X[k]的函数关系h(X(k),k)可以通过横向经纬度与经纬度之间的变换得出如下

(23)

4 构建基于横向坐标系的无迹卡尔曼滤波模型

与传统直角坐标系下的滤波不同，横向地球坐标系下，第三方引导信息进行目标观测时的观测方程是复杂的非线性方程，传统的用于非线性系统的扩展卡尔曼滤波不再适用，无迹卡尔曼滤波(unscented Kalman filter)避免了对非线性模型的线性化处理，不需要对雅可比矩阵求导，比扩展卡尔曼滤波有更高的估值精度[13-15]，因此本文提出将UKF算法运用到横向地球坐标系下的超视距目标跟踪中。

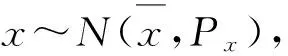
(24)

(25)

(26)

(27)

(28)

(29)

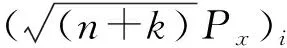
yi=f(χi),i=1,2,…,2n+1.

(30)

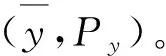
(31)

(32)

构建UT变换模型后，可以进行UKF滤波，为了对本文建立的高纬度地区第三方引导下的超视距目标指示模型进行验证，下面进行仿真与分析。

5 仿真与分析

仿真条件设置如下：

假设目标初始经纬度为(100°,78°) ，即初始横向经纬度为(-2.113 8°,11.815°)，初始横向航向为。如表1所示，目标首先作匀速直线运动，然后直线加速又直线减速，紧接着，目标以恒定速率作蛇行机动，然后，目标再作直线加速，最后以一恒定速率匀速直线运动。

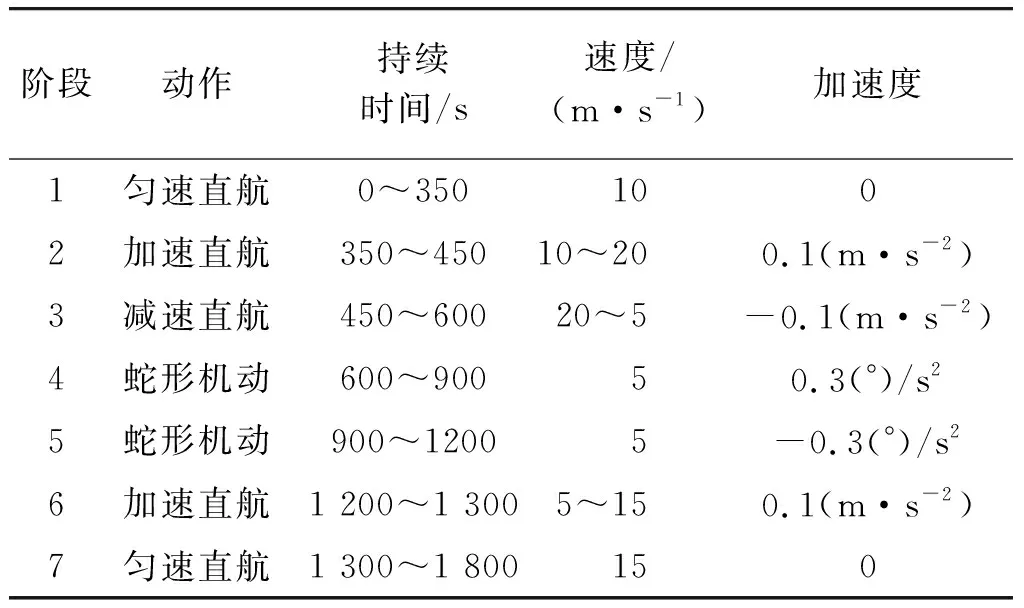
表1 目标运动轨迹Table 1 Target trajectory

假设仿真实验目标运动的初始状态值为X(0)=(-2.113 8°,11.815°,10,36.87°,0)T、P(0)=diag(10-6,10-6,100,100,1)，系统噪声阵为Q(k)=diag(10-8,10-8,1,1,0.01)。目标运动轨迹如图4所示。目标速度变化曲线如图5所示。

根据前文构建的基于横向地球坐标的极区超视距目标运动模型和观测模型，采用UKF算法进行滤波，UKF参数设置：(α=0.01，β=2，k=0)滤波采样间隔T=10 s，对采用第三方引导信息进行目标观测的2种情况进行了仿真实验。

(1) 对第三方仅提供目标位置(经纬度)的情况进行仿真。

假设位置误差为1 n mile，观测噪声为R(k)=diag((1 852/(r·cosφ))2，(1 852/r2)，采用UKF算法进行滤波，将得到的位置估计与目标的真实运动轨迹的比较结果如图6所示；并进行50次蒙特卡罗(Monte Carlo)仿真得到各测量时刻的位置均方根误差，如图7所示。

(2) 对第三方可提供目标位置(经纬度)、速度、航向的情况进行仿真。

假设位置误差为1 n mile，速度误差0.1 kn，航向误差0.1°。则观测噪声为，R(k)=diag((1 852/(r·cosφ))2,(1 852/r)2,0.01,(0.5π/1802))采用UKF算法进行滤波，将得到的位置估计与目标的真实运动轨迹的比较结果如图8所示；并进行50次蒙特卡罗(Monte Carlo)仿真得到各测量时刻的位置均方根误差，如图9所示。

由图6～9可以看出， UKF算法对目标位置跟踪的效果是非常好的，初始状态下, 滤波曲线能很快收敛到真实航迹附近，跟踪曲线也比较平稳。当第三方引导时，增加目标速度和航向观测信息时，比仅提供位置进行观测的跟踪效果好。仿真分析的结果表明：基于横向地球坐标系的极区超视距引导中的目标跟踪模型，避免了坐标系间的多次转换，提高了目指信息的精度。

6 结束语

针对传统超视距目标指示中将目标的位置信息转换到以融合中心为原点的平面直角坐标系中进行目标指示所引入的目指信息偏差问题，提出将横向地球坐标系引入极区超视距目标指示系统中，将目标位置用唯一的一组横向地球坐标来描述。通过构建基于横向地球坐标系的大地主题解算模型，将目标的位置信息转换到横向地球坐标系中，进一步建立基于横向地球坐标系的目标运动模型和目标观测模型，并针对由此产生的目标状态方程和观测方程的非线性特性，提出基于UKF算法的滤波模型，仿真分析的结果表明，该模型有效提高了超视距目标跟踪精度，能够有效满足极区舰艇作战指挥需求。

参考文献：

[1] 谭飞勇,曹之新,郑晓晖.引导兵力确定目标位置方法及精度研究[J].舰艇电子工程,2010,30(5):94-97.

TAN Fei-yong,CAO Zhi-xin,ZHENG Xiao-hui.Research of Method and Precision on the Lead Troops Decision Object Position[J].Ship Electronic Engineering,2010,30(5):94-97.

[2] 王德强,黄双华,刘峰,等.岸基雷达超视距引导误差分析[J].舰艇电子工程,2008,28(12):89-91.

WANG De-qiang,HUANG Shuang-hua,LIU Feng,et al.Analysis of OTH Leading Error by Radar Eased on Shore[J].Ship Electronic Engineering,2008,28(12):89-91.

[3] 王钢,贾世楼,张琦.超视距目标指示的方法与性能研究[J].哈尔滨理工大学学报,2006,11(6)：110-113.

WANG Gang,JIA Shi-lou,ZHANG Qi.Study on the Methods and Performance of OTHT[J].Journal Harbin Univ.Sci & Tech,2006,11(6)：110-113.

[4] 朱汉雨,荣海洋.侦察兵力通过数据链传递目标指示的方法探讨[J].指挥控制与仿真,2007,29(1)：61-62.

ZHU Han-yu,RONG Hai-yang.Methods of Scouting Plane Transmitting Object Information to Submarine Through Data Link[J].Command Control & Simulation,2007,29(1):61-62.

[5] 朱士龙,张佳忠,顾浩.超视距目标信息仿真测试技术研究[J].系统仿真学报,2004,16(8):1701-1704.

ZHU Shi-long,ZHANG Jia-zhong,GU Hao.Research on Beyond Visual Range Target’s Information Simulation Test Technology[J].Journal of System Simulation,2004,16(8):1701-1704.

[6] 吴云桥,段立,耿伯英.基于大地坐标的多舰协同超视距目标指示研究[J].舰艇电子工程,2008,28(10):60-63.

WU Yun-qiao,DUAN Li,GENG Bo-ying.Research on Multi-Warship Collaboration over Horizon Target Indication Based on Geodetic Coordinates[J].Ship Electronic Engineering,2008,28(10):60-63.

[7] 卢江涛,杨露菁,段立.一种应用于超视距目标指示的误差分析方法[J].指挥控制与仿真,2007,29(2):88-91.

LU Jiang-tao,YANG Lu-jing,DUAN Li.An Error Analysis for Over-Horizon Target Designation[J].Command Control & Simulation,2007,29(2):88-91.

[8] 徐清华,徐海刚,李中良.直升机超视距主动引导定位误差分析[J].指挥控制与仿真,2006,28(10):60-63.

XU Qing-hua,XU Hai-gang,LI Zhong-liang.Analysis on OTH Active-Guiding Positioning Error for Helicopters[J].Command Control & Simulation,2006,28(10):60-63.

[9] 赵凯,杨维,石德乾,等.自行装备间目标指示与导引精度分析[J].火炮发射与控制学报,2010(1):71-75.

ZHAO Kai,YANG Wei,SHI De-qian,et al.Analysis on Target Indication and Guidance Accuracy Among Self-Propelled Equipments[J].Journal of Gun Launch & Control,2010(1):71-75.

[10] 张鑫博,杨晓萍.数据链远程目标指示位置误差计算方法研究[J].现代电子技术,2014,37(2):13-15.

ZHANG Xin-bo,YANG Xiao-ping.Calculation Method for Position Error of Data Link Remote Target Designation[J].Modern Electronics Technique,2014,37(2):13-15.

[11] 邱云峰,倪津,杨映泉,等.基于CGCS2000下地方大地坐标基准的建立与应用[J].测绘工程,2013,22(4):42-44.

QIU Yun-feng，NI Jin，YANG Ying-quan,et al.On the Establishment and Application of Local Geodetic Coordinate Datum Based on CGCS2000[J].Engineering of Surveying and Mapping,2013,22(4):42-44.

[12] 孙晏涛.水面舰艇运动仿真模型研究[J].舰船电子工程,2011,31(6):118-121.

SUN Yan-tao.Research on Surface Ships Motion Simulation Model[J].Ship Electronic Engineering,2011,31(6):118-121.

[13] 陈云峰.目标跟踪中非线性滤波[D].南京:南京理工大学,2007.

CHEN Yun-feng.Nonlinear Filter of Target Tracking[D].Nanjing:Nanjing Science and Engineering University,2007.

[14] 于翔川.基于非线性滤波的目标跟踪算法研究[D].西安:西安电子科技大学,2009.

YU Xiang-chuan.Target Tracking Algorithms Based on Nonlinear Filtering[D].Xi′an：Xidian University,2009.

[15] 侯磊.机动目标跟踪算法的研究[D].大连：大连海事大学,2015.

HOU Lei.The Research on Maneuvering Target Tracking Algorithm[D].Dalian:Dalian Maritime University,2015.