高速移动环境大规模MIMO信道建模与性能分析

邹劲柏，谢 浩，艾 渤,2，郭爱煌,2

(1.同济大学 电子与信息工程学院，上海 201804；2.北京交通大学 轨道交通控制与安全国家重点实验室，北京 100044；3.上海应用技术大学 轨道交通学院，上海 201400)

几何随机分布模型GBSM (Geometry-based Stochastic Model)分为两类：纯GBSM和半GBSM。半GBSM也称为参数化的随机模型PSM(Parametric Stochastic Models)。PSM通过总结通用参数、大尺度参数和小尺度参数生成信道系数，应用路损与衰落完成建模，需要大量的实测数据[1-2]。纯GBSM模型中，无线传播特性取决于散射体的分布特性。不同形状的散射物分布也对应有不同的模型，比如单环模型、双环模型和椭圆模型等[3-4]。在实际应用方面，纯GBSM与物理环境有着直接联系，模型可以通过修改散射簇的随机分布、特性和散射区域的形状来适应不同的场景。此外，能够通过简单的几何运算计算出模型参数，因此被广泛应用[5-8]。

使用GBSM进行建模有两个重要优点,首先，模型有着直观的几何意义，便于理解和使用。其次，几何信道模型在进行运动仿真时具有优势。无论何时，只要移动台移动，多径分量的参数调整都是自动进行的。因此，从运动过程中可以自动得到正确的空时相关性，同时考虑了移动台处到达角与多普勒频移之间的相关性。由移动台大尺度运动引起的到达角、离开角和时延的任何改变都会自动包括在内。

本文基于GBSM信道建模方法，建立高速铁路系统中深沟堑场景下Massive MIMO的3D信道模型，对信道统计特性中的时空特性进行分析与仿真。Massive MIMO系统容量的扩展以及系统可靠性的提高，都依赖于无线信道的多径传播，因此研究传播信道的空时特性，并建立Massive MIMO信道模型显得尤为重要。

1 基于GBSM的深沟堑场景三维信道模型

作为高速铁路运输系统最普遍的场景之一，沟堑被用来确保列车的高速运行和铁轨的平坦。沟堑通常建造在不平坦的土地上或者从山体中挖出，铁轨两边山体的高度以及倾斜度都一样。沟堑可以被分为两种类型：深沟堑和浅沟堑，这取决于沟堑的顶部是否高于列车的天线。重点考虑深沟堑场景，由于深沟堑的墙面导致了大量的反射和散射，因此传播特性与铁路的其他场景有着很大不同。典型的深沟堑场景如图1所示。

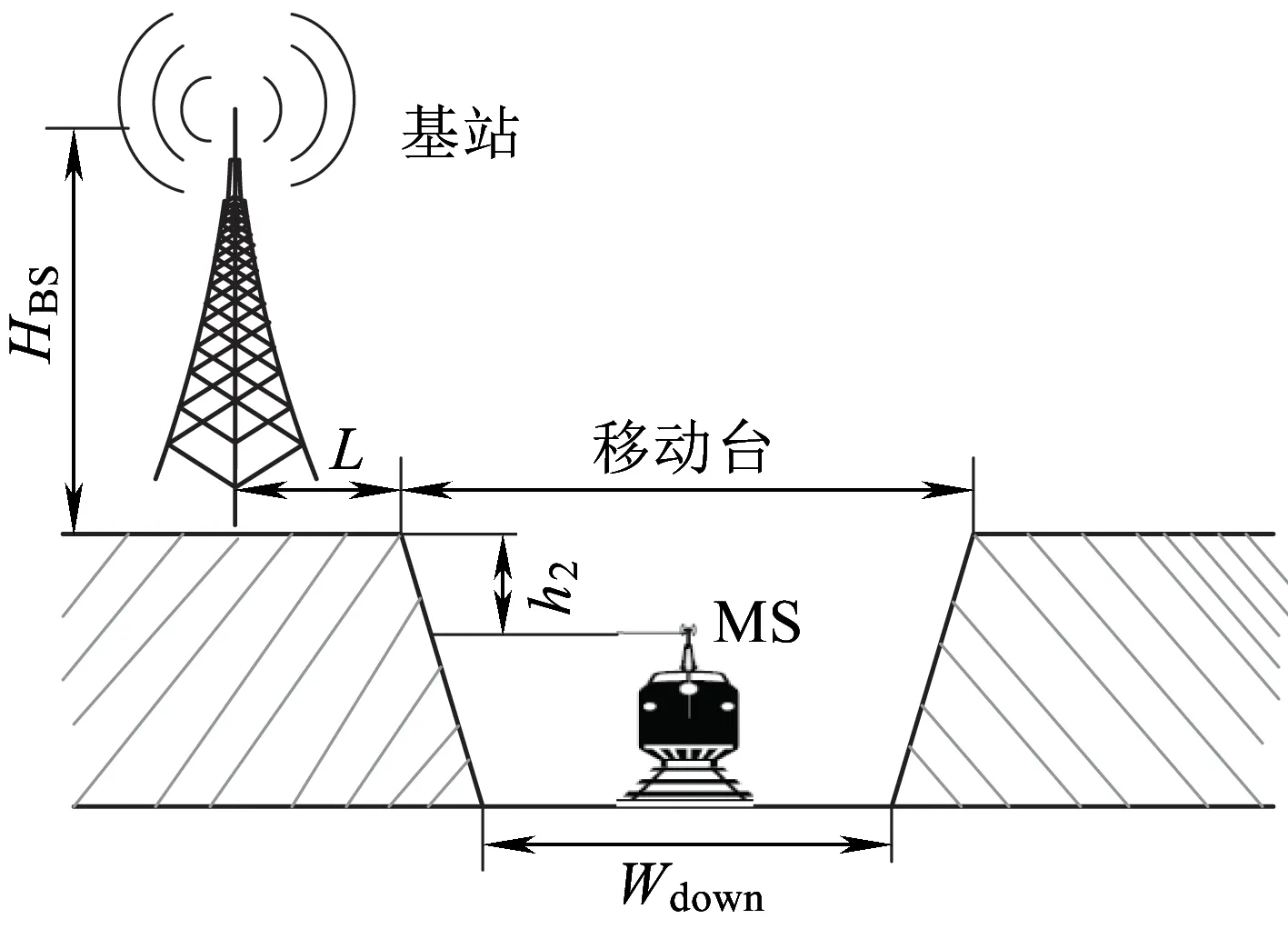
图1 深沟堑场景

深沟堑场景的散射体表面和绕射边可以使用垂直圆柱进行建模。假设圆柱模型所有的实际散射体都可以等价为随机分布于圆柱体表面的等效散射体。虽然峭壁不是垂直的表面，其表面通常被杂草和钢筋混凝土覆盖，发生漫发射。斜坡的长度相比基站到移动台的距离较短，两边斜坡的长度和深度都相同，形成了一个峡谷。在文献[9]中，圆柱已经被证明了适合用于峡谷地形的建模。

对于大规模MIMO来说，不平衡特性表现为当一个天线阵列很大时，不同物理位置的天线会受到不同的散射体影响，如图2所示。但是这种不平衡特性只在大量天线(例如：128天线)排布在同一纬度上时发生。在实际天线架设中，天线在平面阵上排布，单一维度的天线尺寸没有那么大，需要考虑天线尺寸的不平衡特性[10-12]。

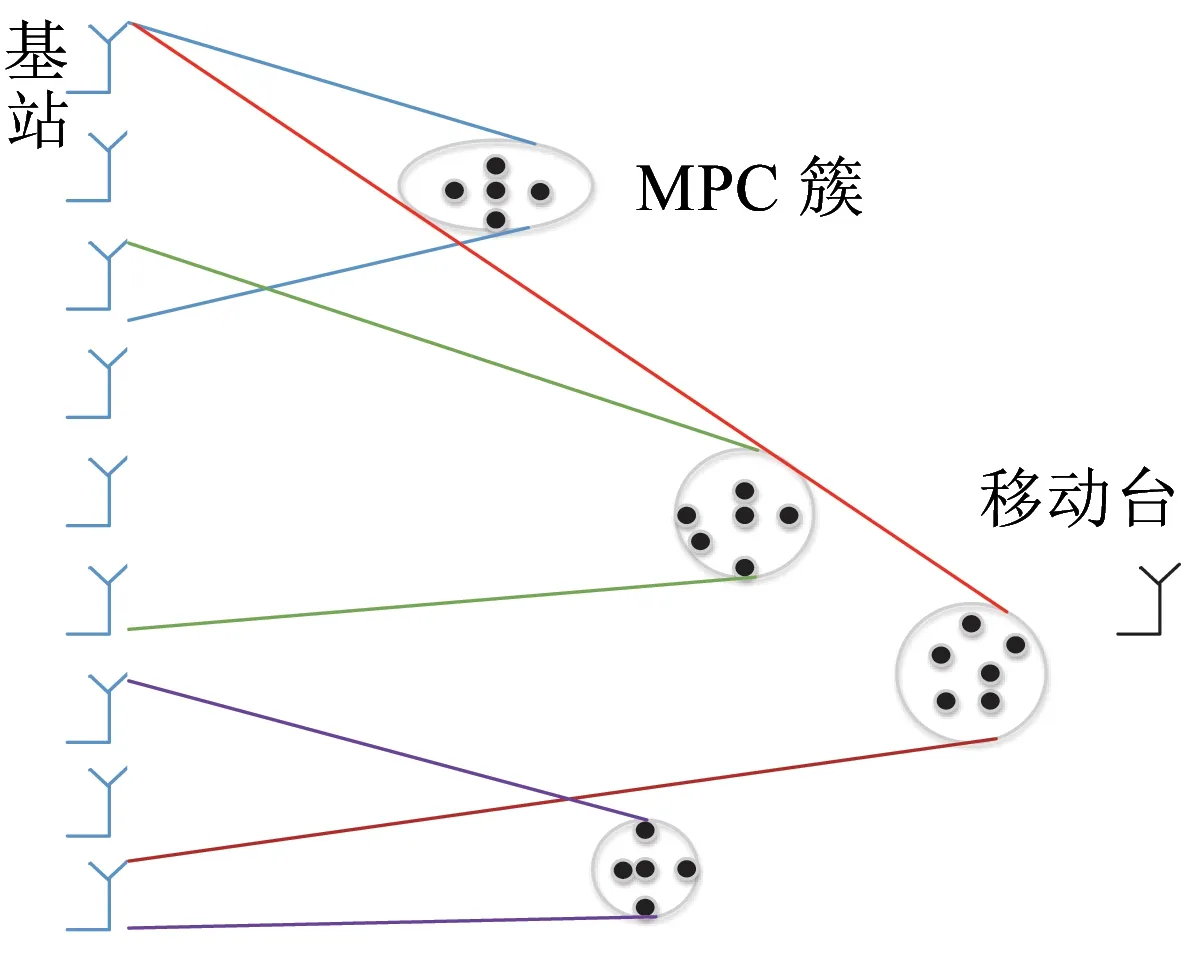
图2 不平衡特性

为了表征不平衡特性，在圆柱模型的基础上增加了球体模型，如图3所示。每一个天线的“可见”范围都用虚拟球体表示，等效散射体只有在其与特定天线距离小于球体半径时才会对天线产生影响。每个天线都由一个以天线本身为球心、半径为r的球体来确定其 “可视”散射体。等效散射体由散射体本身的角度信息决定，反映了散射体对于信号幅度、相位和时延的影响。文献[10]的测量结果表明，两个天线元素间的特定距离是可知的，其信道冲激响应间的相关系数可以看作一个常值，这个值反映了它们之间共享散射体数目的多少，相关系数越大则共享散射体数目越多。根据距离和相关系数，球体的半径可以通过计算得出。

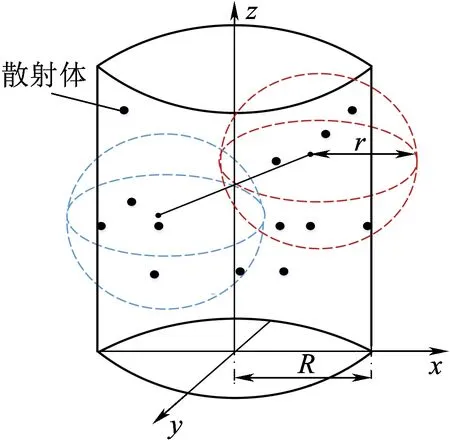
图3 圆柱-球体模型

假设有两个天线元素，在相同的水平面上并且关于圆柱的中心纵轴对称，它们之间的距离为λ/2(λ为波长)。假设信道脉冲相关系数为0.9，散射物均匀地分布在圆柱表面，圆柱半径为R，可视球体的半径为r。为了简化运算，三维图像可以被拓展到二维图像中，由文献[4]得出一个近似值为

r>R×2.785 6

( 1 )

考虑一个下行Massive MIMO信道，基站天线数和移动台天线数分别用LT和LR表示，天线元素的序号1≤p≤p′≤LT，1≤q≤q′≤LR。为了简化分析，以一个2×2信道为例。模型中的天线数可以拓展到任意数目，天线阵列也可以是任意形状。

图4所示模型在几何上由LOS和单跳路径组成，跳转发生在从接收端圆柱体表面的等效散射体到接收天线元素的过程之中。有N个等效散射体分布在移动台周围的一个半径为R的圆柱表面上，第n个散射体用S(n)表示。由于深沟堑场景的特点，散射体集中分布于移动台周围，因此只考虑分布在接收端的散射体。值得注意的是，为了显著地降低3D GBSM理论信道模型的复杂度，只考虑了直射路径和单跳路径，其他跳转路径都被忽略，因为实际上这些不同的跳转路径只是反映了相同的信道统计特性。

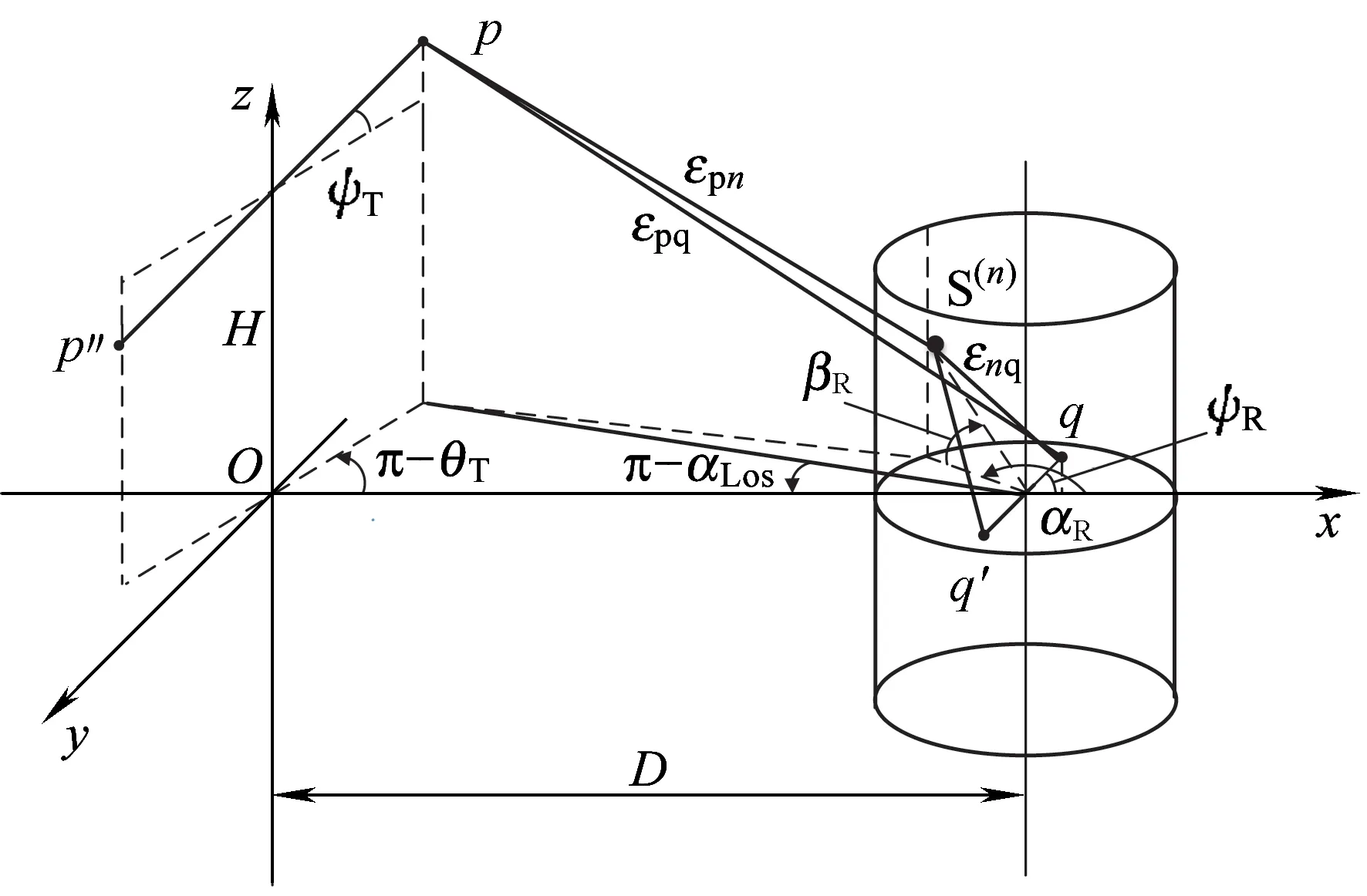
图4 GBSM几何模型

基于图4描述的GBSM，信道的信道脉冲响应CIR(Channel Impulse Response)hpq是LOS和N-LOS的叠加，CIR可以表示为

( 2 )

式( 2 )中，LOS成分为

( 3 )

式( 2 )中，N-LOS成分为

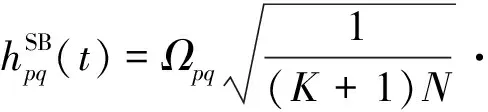
( 4 )

式中：Ωpq为子信道pq的传输功率；K为子信道pq的莱斯因子；λ为载波波长；fmax为移动台的最大多普勒频移；γR为列车运行方向与x轴的夹角；相位φn为随机变量，在[-π，π)之间均匀分布，独立于到达角AoA(Angel of Arrival)。

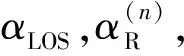
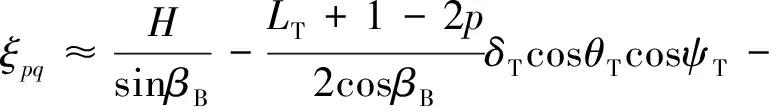
( 5 )

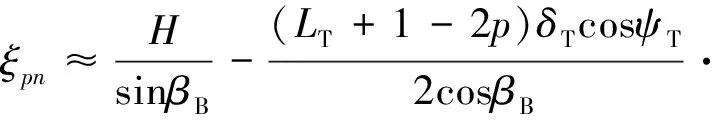
( 6 )

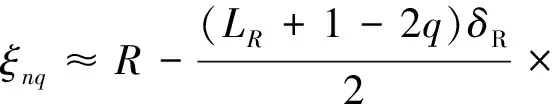
( 7 )

式中：βB为基站相对于x-y平面的仰角，βB=arctan(H/D)；Δ≈arcsin(R/D)。当max{δT，δR}≪R≪D时，R/D是传播的窄角。对方位角α进行窄角近似，也就是sinα≈α，cosα≈1。

2 Massive MIMO的GBSM统计特性

Massive MIMO系统利用无线信道的多径传播，开发空间资源，建立空间并行矩阵传输通道，利用空时联合处理提高无线通信系统的容量与可靠性[11-13]。然而，决定空时处理性能的关键因素在于无线传播信道的空时特性。一方面，对于Massive MIMO通信系统，有效利用多径传播是Massive MIMO系统的重要特点，其高性能的获得与传播环境的散射传播密切相关，因为传播环境中散射的分布情况决定了多径的丰富程度，从而影响到Massive MIMO信道的性能。另一方面，收发多天线系统是Massive MIMO无线系统的重要组成部分，它们在无线链路中起着重要作用，其性能也直接决定Massive MIMO信道的性能。可见，Massive MIMO系统的性能与两个因素密切相关，即散射传播环境和多天线性能，将二者联系起来将十分有利于分析Massive MIMO系统。联系二者的重要途径就在于分析Massive MIMO信道的空域和时域的相关性。

2.1 空时相关函数STCF

在广义平稳非相关散射WSSUS条件下，两个子信道hpq(t)和hp′q′(t)之间的STCF定义为

( 8 )

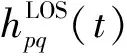
( 9 )

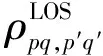
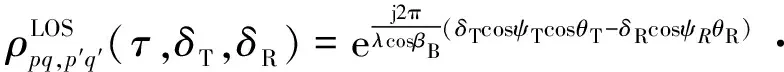
(10)

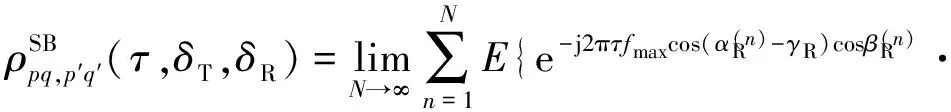
(11)

式中：βmax为随机散射物的最大仰角；γR为列车行驶方向和x轴的夹角。假设散射环境是各向异性的，Von Mises概率密度函数PDF(Probability Dense Function)和Parson PDF，被分别用来描述散射物到达角的方位分量和倾斜分量，von Mises PDF为

f(θ)=ekcos(θ-μ)/(2πI0(k))

(12)

式中：θ∈[-π，π);μ∈[-π，π)为分布在水平平面的散射物的平均角度；Ι0()为第一类零阶修正贝塞尔函数；k为一个正实数，表示在平均角μ附近散射物的传播，随着k的增大，散射物的各向全异性增强。

Parson PDF定义为

(13)

式中：φmax的变化范围是[0，20°]，是最大的仰角，这样的最大仰角是“街道-峡谷”传播模式的特征。深沟堑是HST系统典型的“街道-峡谷”，所以Parson PDF是适用的。如

(14)

SB成分的STCF可以简化为

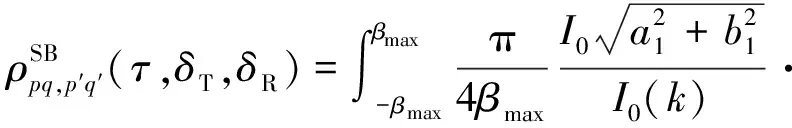
(15)

其中

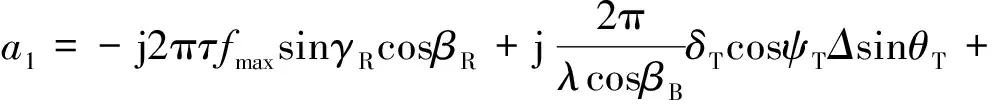
(16)

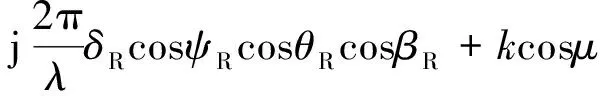
(17)

在式(15)中，SB成分的STCF必须进行数值分析，因为这个积分是没有封闭解的。在深沟堑场景中，βR的最大值都小到可以进行窄角近似，cosβR≈1，sinβR≈βR，因此，式(15)中的STCF可以近似为

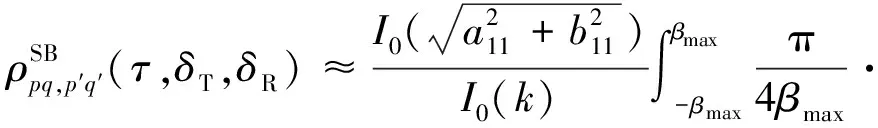
(18)

其中

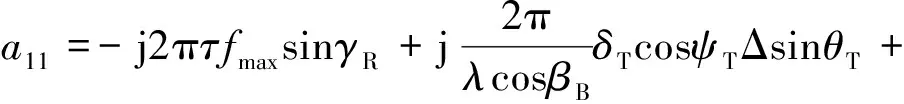
(19)

(20)

最后，求解式(18)中的积分，可以得出近似的STCF封闭解为

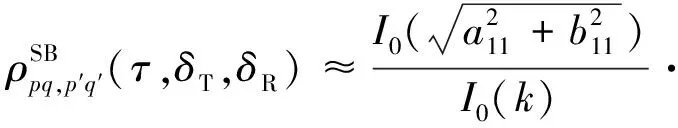
(21)

2.2 空间互相关函数

通过在式(10)、式(15)中设定τ=0，可以从STCF中得到空间CCF，即

(22)

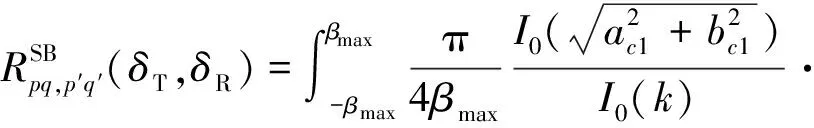
(23)

其中

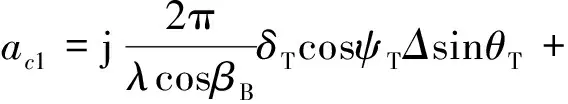
(24)

(25)

2.3 多普勒功率谱密度PDF

信号传播时，信道特性会由于选择性衰落而发生改变，移动台和基站之间的运动或者路径中物体的运动都会产生时间选择衰落信道。信号的球面传播会导致相同阵列中的不同天线经历不同的多普勒频移，因此，天线阵列的多普勒频移也许会改变。通过对时空相关函数进行傅里叶变换，可以得到相应的多普勒PSD。

(26)

式中：fD为多普勒频移；F{}为傅里叶变换。

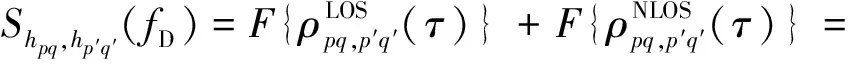
(27)

3 仿真结果

3.1 STCF闭式表达式验证

仿真使用的载波频率为2 GHz，基站天线高度为28 m，移动台天线高度3 m，低于沟堑斜坡的高度，基站天线相对于移动台天线高度H=31 m，接收端圆柱半径R=30 m，基站和接收端圆柱中心的水平距离为D=500 m，随机散射体的最大仰角βmax=arctan(3/15)，最大多普勒频移为fmax=200 Hz。通过在数值上对比式(21)和式(15)的STCF来证明近似的正确性，图5和图6分别显示倾斜角ψT=ψR=π/4、方位角θT=θR=2π/3和ψT=ψR=π/5、θT=θR=π/2时，式(15)和式(21)STCF的绝对值。结果表明两种情况下除了几个特定点，大部分情况下精确值和近似值都很接近，这也表明提出的STCF闭式表达式是正确的。

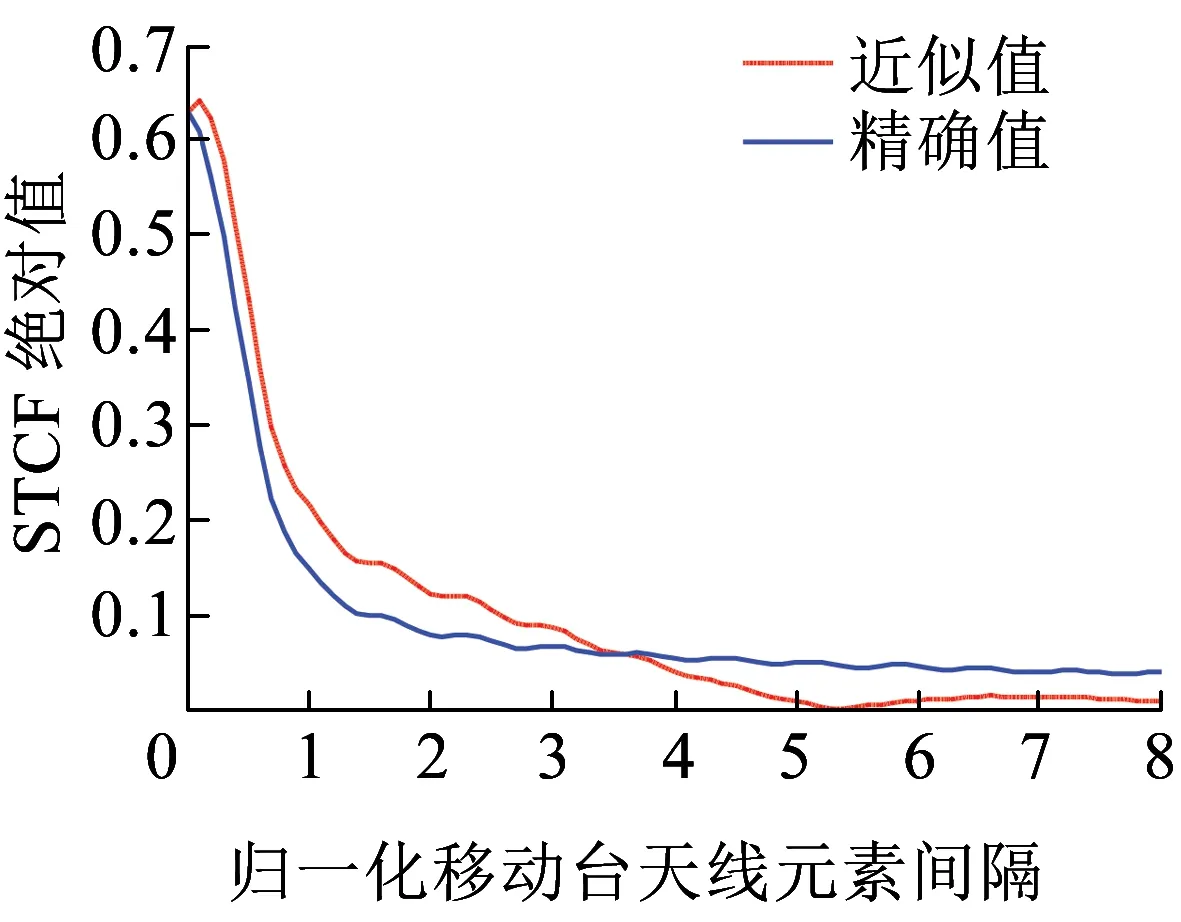
图5 式(15)和式(21)的STCF绝对值(ψT=ψR=π/4，θT=θR=2π/3，k=3，σT=0.5λ)

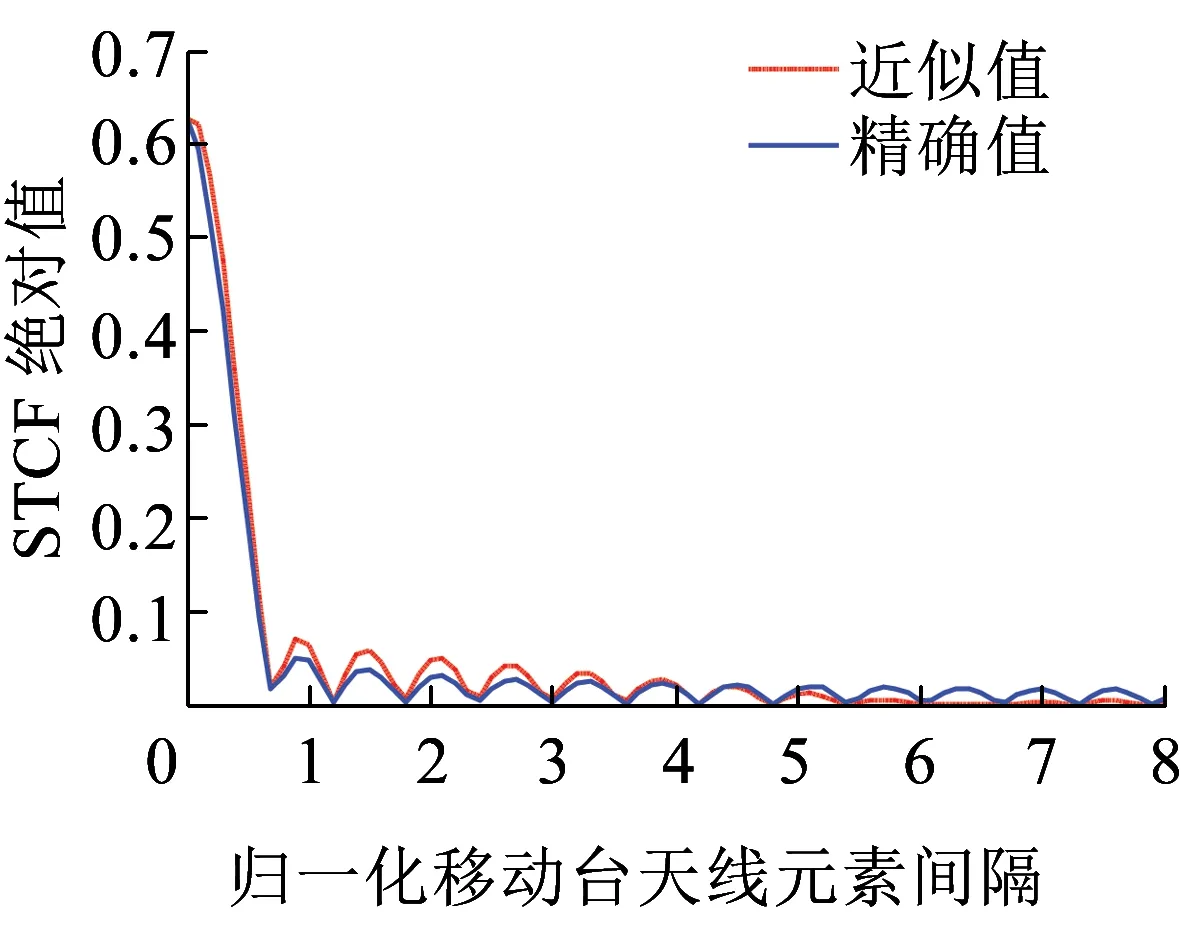
图6 式(15)和式(21)的STCF绝对值(ψT=ψR=π/5，θT=θR=π/2，k=3，σT=0.5λ)

3.2 3D与2D模型CCF对比

当βR=0时，圆柱模型就变成了2D圆环模型。图7和图8展示了2D和3D模型的空间CCF绝对值的差异，显然3D模型的空间CCF绝对值要低于相关2D模型。因为现实中的空间多样性包括了垂直和水平两个部分，2D模型忽略了垂直部分，导致对于空间CCF的过高估计，这也和文献[8]中的结论相同。

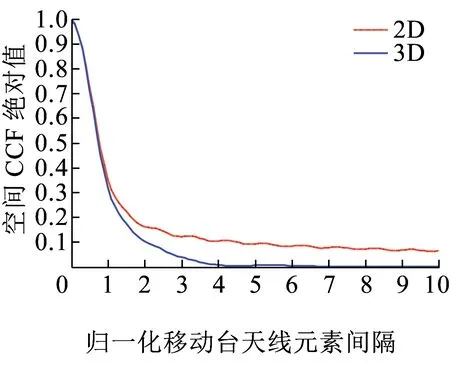
图7 CCF绝对值(ψT=ψR=2π/3，θT=θR=2π/3，k=3，σT=0.5λ)

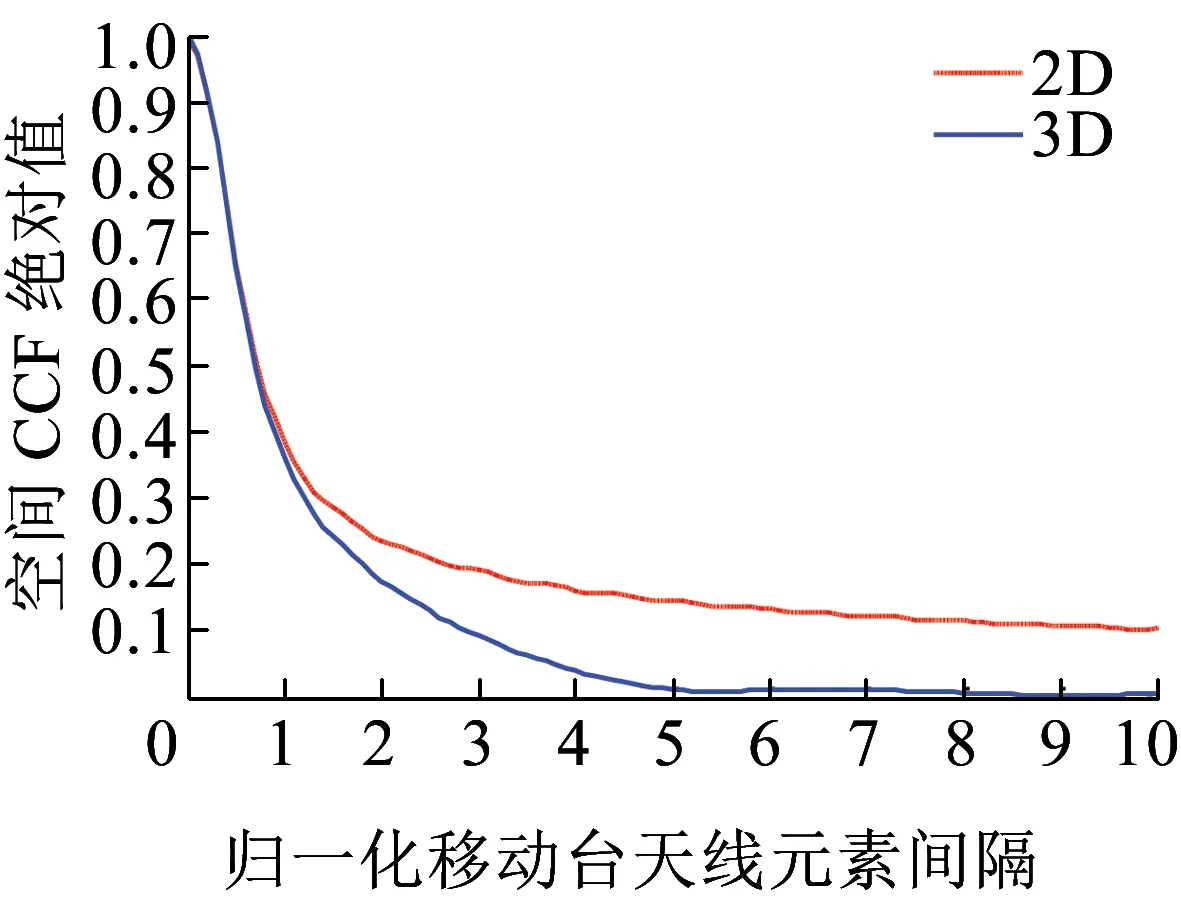
图8 CCF绝对值(ψT=ψR=3π/4，θT=θR=3π/4，k=3，σT=0.5λ)

3.3 垂直维度对于STCF的影响

对比2D模型，3D模型对于基站和移动台天线阵列的仰角ψT、ψR进行了建模，图9显示了ψT和ψR对STCF的影响情况，为了更好地展示收发两端的仰角改变所带来的不同影响，使用3D绘图。图9表明当ψR>0时，STCF结果的绝对值随着移动台天线阵列仰角ψR的增加而迅速减小。当ψR<0时，STCF结果的绝对值随着移动台天线阵列仰角ψR的增加而增大。当基站天线阵列的仰角变化时，STCF的值变化较慢。

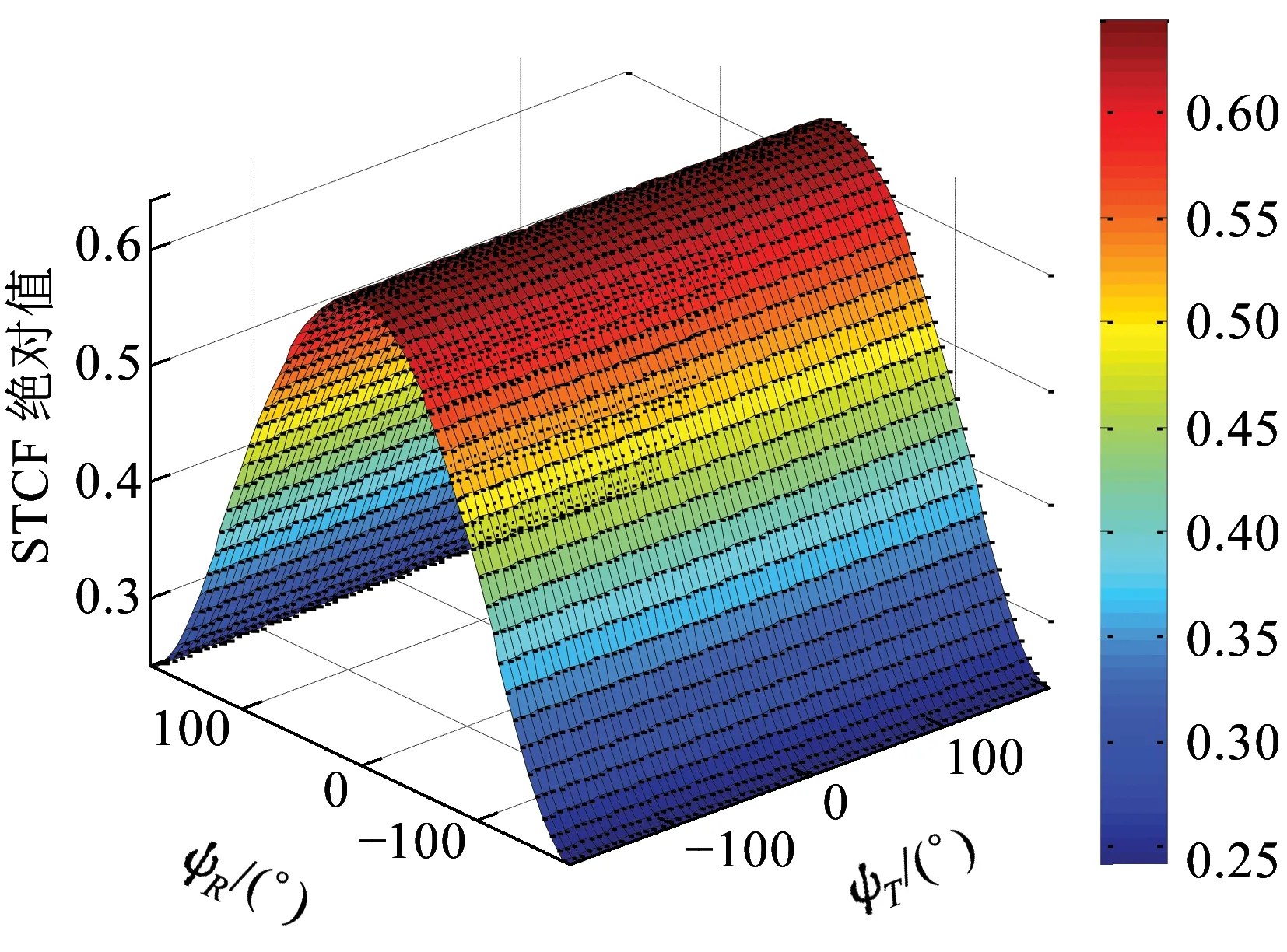
图9 基站和移动台垂直方向STCF的绝对值(δT=δR=0.5λ，θT=θR=2π/3，k=3)

4 结束语

目前Massive MIMO的研究和应用处于探索阶段,其在高铁场景下的应用更是少有具体研究。有别于Massive MIMO技术在公网场景下的应用研究,铁路场景多是规律的带状网络拓扑,基站与列车间以点对点通信为主,且列车在尺寸及发送功率等方面比传统小区接收终端都具有优势。因此,根据高铁场景特性,开展高移动性及铁路通信网络架构下的Massive MIMO技术应用研究具有重要的理论及现实意义。

为深沟堑场景下高速铁路HST无线通信系统的各向异性大规模MIMO莱斯衰落信道提出了一个基于几何随机分布的3D信道模型GBSM。加入对垂直维参数的建模，可以比以往2D模型更好地还原实际的无线传播场景。通过分析统计信道模型的统计特性，使用已证实的近似值进行推导，得出了信道空时相关函数STCF的闭式表达式。通过MATLAB信道仿真，证明了空时相关函数闭式表达式的正确性。在与2D模型空间相关性的对比当中，证明了3D模型相比2D模型在空间相关性上有着更高的准确性。同时，分别研究了基站和移动台这两端新增的维度对于信道模型STCF所带来的影响。结果表明，影响STCF绝对值的主要是移动台天线阵列的仰角，基站侧天线阵列仰角的改变几乎不影响STCF绝对值。

参考文献：

[1]3GPP. TR 36873 VI.2.0，Study on 3D Channel Model for LTE[R]. 3GPP， 2014.

[2]张雅媛. 3D MIMO的信道建模及相关技术研究[D]. 北京：北京邮电大学，2015.

[3]XIANG X， WU M， ZHAO R， et al. Research on High-speed Railway Model for Train-ground MIMO Channel[C]// 2014 International Symposium on Wireless Personal Multimedia Communications (WPMC).New York:IEEE,2014:724-728.

[4]YOU L, GAO X, SWINDLEHURST A L, et al. Channel Acquisition for Massive MIMO-OFDM with Adjustable Phase Shift Pilots[J]. IEEE Transactions on Signal Processing, 2015, 64(6):1461-1476.

[5]XIE Y， LI B， ZUO X， et al. A 3D Geometry-based Stochastic Model for 5G Massive MIMO Channels[C]// 2015

11th International Conference on Heterogeneous Networking for Quality， Reliability， Security and Robustness (QSHINE).New York:IEEE， 2015:216-222.

[6]程梦. 高铁下一代无线通信系统的波束赋形与大规模多天线传输技术研究[D]. 成都：西南交通大学，2015.

[7]AI B, GUAN K, RUPP M, et al. Future Railway Services-oriented Mobile Communications Network[J]. IEEE Communications Magazine, 2015, 53(10): 78-85.

[8]CORVAJA R, ARMADA A G. Phase Noise Degradation in Massive MIMO Downlink with Zero-forcing and Maximum Ratio Transmission Precoding[J]. IEEE Transactions on Vehicular Technology, 2016, 65(10): 8052-8059.

[9]ZAJIC A G，STUBER G L. Three-dimensional Modeling， Simulation， and Capacity Analysis of Space-time Correlated Mobile-to-mobile Channels[J]. IEEE Transactions on Vehicular Technology,2008,57(4):2042-2054.

[10]AI B, CHENG X, KURNER T, et al. Challenges Toward Wireless Communications for High-speed Railway[J]. IEEE Transactions on Intelligent Transportation Systems, 2014, 15(5): 2143-2158.

[11]LIU Y, AI B, GUAN K, et al. Antenna Array Configurations for 3D MIMO System in High Speed Railway Scenario[C]//2015 IEEE International Symposium on Antennas and Propagation & USNC/URSI National Radio Science Meeting. New York:IEEE, 2015: 719-720.

[12]刘留， 陶成， 卢艳萍， 等. 大规模多天线无线信道及容量特性研究[J]. 北京交通大学学报，2015， 39(2)： 69-79.

LIU Liu, TAO Cheng, LU Yanping, et al.Research on the Propagation Condition and Channel Capacity for Massive MIMO[J].Journal of Beijing Jiatong University，2015,39(2):69-79.

[13]张艺引. Massive MIMO确定性建模中的Ray Tracing技术研究[D]. 北京：北京交通大学，2015.