基于轨道相对测量数据识别曲线关键参数的研究

熊丽娟，朱洪涛，魏 晖，刘 敏

(1.南昌大学 机电工程学院，江西 南昌 330031；2.南昌航空大学 航空制造工程学院，江西 南昌 330063；3.江西科技学院 汽车工程学院，江西 南昌 330098)

既有线曲线整正是既有铁路养护和维修业务的重要内容。曲线整正时需根据线路实测数据辨识曲线特征点(主点)和参数并拟合出一条最贴近实际曲线的理想曲线，结合整正原则、约束条件，通过柔性拟合得到最终的整正曲线[1-2]。

国内文献多将识别理想曲线参数这一步省略，直接求解使总拨道量最小的标准曲线作为整正曲线[3-9]。这种优化过程实为刚性拟合。刚性拟合易产生冗余拨量，长此以往会加重轨道变形，使其难于整正[2]。因此，长远来看，应该在理想曲线的基础上通过柔性拟合得到更贴合实际的整正曲线。因此，精确识别出理想曲线(识别出其关键参数)，是铁路整正的关键。

国内常见的曲线关键参数识别过程如下：首先将平面空间数据转换成参数空间数据(如曲线正矢等)以识别曲线特征点，再按特征点分段将平面空间数据拟合优化，得到圆曲线半径和缓和曲线长[3-5, 10-12]。上述方法基于平面空间数据，而平面空间数据测量的效率、精度难以满足轨道平顺性控制的要求；另外在正矢识别曲线特征点的过程中，由于粗大误差的存在，现行的最小二乘拟合缺乏稳健性。

本文旨在通过轨道检查仪(以下简称轨检仪)的相对测量数据，提出一种更高效的理想曲线识别方法。在本文中该方法主要针对铁路上的单曲线。标准单曲线由圆曲线和第一、第二缓和曲线共同构成，其线形和在线路上的位置由以下5个参数定义[13]：直缓点ZH、缓圆点HY、圆缓点YH、缓直点HZ和圆曲线半径R。这5个关键参数相互独立[13]，其中ZH、HY、YH、HZ点即常说的四大特征点。

1 识别原则

文献[3]中提到，通常情况下，铁轨虽有错动，但线形偏移是微小量，因此可认为拟合的理想线形可以一定精度逼近原始设计线形。

如图1所示，当直线线路的测点中只有一个点发生错动时，若直接以拨距平方和最小为优化目标，用最小二乘法拟合，所得直线必偏离设计线；据此整道一段时间后，若该线路再发生同类错动，继续以上述方法处理，则整正目标曲线会继续偏离设计线；长此以往，最终会导致该段线路远离设计线，难以再度整正或者两端出现“鹅头”。在此例中，若以使拟合线上测点数目最多为目标，则拟合出的直线即为设计线，此时只有一点需拨道；对比最小二乘法，此法不易导致曲线未来难以整正。由此可见，以点数最大化为目标拟合出的曲线更贴合实际，更靠近设计，更适合作为拨道的理想曲线。宜在理想曲线的基础上柔性拟合，以得到相对拨道量最小的整正曲线(不必须为标准曲线)。

图1 只有一点发生错动的夹直线

2 数据准备

识别曲线四大特征点通常基于正矢图、曲率图或超高图，而曲线半径则通过角图、曲率图、绝对坐标曲线拟合来判别(部分文献通过超高判别)[2-12, 14-15]。

坐标法整道中，正矢图或曲率图常常通过中线绝对坐标数据推导得出[4-6, 10, 12, 14]。由于所测绝对坐标本身属离散数据，不方便求导，所以通常先将其拟合得到连续函数或二阶导连续函数，再计算正矢或曲率。上述过程较繁琐，实际上，通过相对测量就可直接得到正矢。

目前的相对测量轨检仪使用高精度光纤陀螺仪(FOG)测轨向转角，测点间距为0.125 m，而目前绝对测量点间距一般在0.65 m左右，即一个轨枕间距。而且，绝对测量效率比相对测量低得多，测量精度除与全站仪本身精度相关外，还与CPⅢ网的精度相关。假设相对测量使用的FOG零漂为0.5°/h(一般精度水平)，在FOG的地球自转影响补偿较好情况下，10 m轨向误差约为±0.1 mm。相比之下，当绝对测量中使用一般精度(如1"精度等级)的全站仪，10 m轨向的测量中误差可达0.9 mm[16]，由此推断其误差约为±2.7 mm。显然，相对测量的短波精度比绝对测量的短波精度高。因此，采用相对测量的正矢识别理想曲线参数比用绝对测量数据得到的正矢精度高。

将相对测量中测得的每0.125 m的水平转角从某一点(起点)开始累加，得到每个测点的累积转角。以累积转角为纵坐标，以测点距起点的里程为横坐标画出的曲线图即为角图。角图起点一般设于夹直线上，以右向转角为正。角图的特点是：测距越大，累加次数就越多，越有利于消除测量随机误差，增强数据的抗干扰性。

因为角图的线下面积即为渐伸线长，优化设计后的角图曲线是否满足整正原则直观明了，计算拨距也方便，传统的铁路整正过程中常使用角图选配曲线半径、计算拨距。虽然基于渐伸线法的传统整正方法有被坐标法取代之势，但利用角图来确定曲线的关键参数(如圆曲线半径)仍然比较方便。

图2为某铁路上行线中一段单曲线的正矢图、角图和超高图，为使用江西日月明轨检仪(FOG零漂小于0.5°/h)检测所得。其设计曲线半径为800 m，四大特征点为：ZHs=668 768 m,HYs=668 938 m,YHs=669 323 m,HZs=669 493 m。图2中(a)～(c)3个分图的偏差均值分别为-0.033 6 mm、-0.131 4°和2.594 4 mm，中误差依次为2.883 3 mm、0.121 9°和3.362 1 mm。

(a)正矢图

(b)角图

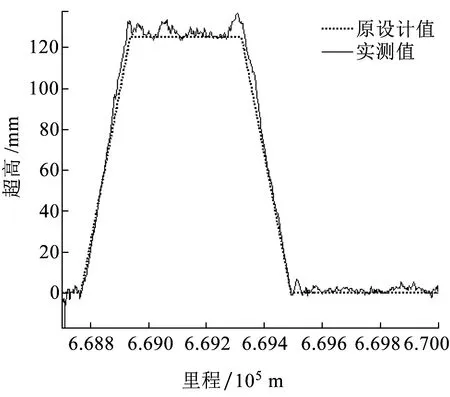
(c)超高图图2 某实际线路的相对测量数据图

对比图2(a)和图2(b)发现：正矢设计值虽为五段直线，但实测值中高频干扰大，波动较大，线性不良；角图因为积分带来的低通性和稳健性，高频干扰和波动均较小，与设计值较贴合。但从识别曲线参数的方便性看，正矢图较有优势，因为只需拟合直线求交点即可。

对比图2(a)和图2(c)发现：超高图与正矢图相似，因为在设计时这两者基本是成正比的；超高实测值的高频干扰比正矢中小，这是两者的采样频率和测量用传感器特性不同的缘故。

超高图的以上特点使部分学者认为其比正矢图更适合用来识别特征点[11]，但这并不科学。因为特征点是平面曲线的线型分割点，而实测超高并非平面曲线上的物理量，而是独立于平面曲线的一个参数。另外，无论在高速铁路上还是在普速铁路上，超高实际均采用曲线顺坡，而非直线顺坡，因此对超高图通过拟合直线求交点来识别其折变点位置误差较大。综上，超高图不适用于特征点和半径的精确识别。

由上述可知，相对测量中比较适合用来识别理想曲线关键参数的数据是正矢图数据和角图数据。

3 拟采用的基本识别算法

本文将拟合线上测点数目最大化作为理想曲线的识别原则。因此在处理正矢图和角图时，也将此作为曲线拟合的原则。

在拟合直线时，为满足上述拟合原则，应用了图像处理中的霍夫变换方法，以识别出主直线；再用稳健估计法对主直线上的点拟合，得其直线方程。将霍夫变换与稳健估计法联合使用，可解决直接使用霍夫变换时拟合精度不高的问题[17]。

关于稳健估计法，文献[14]中有详细论述，本质上它是一种变加权的最小二乘迭代法。本文中此法采用的权值决定方法为：当实测与拟合之差大于拟合均方根的3倍时，将此实测点权值设为0，否则权值为1。

正矢图中，设计线图为五段直线，分别对应夹直线、第一缓和曲线、圆曲线、第二缓和曲线和夹直线，其中第一和第五段在同一直线上。因此，对实际正矢图，只需用上述霍夫加稳健算法拟合出四条主直线，再求对应交点就能得到四大特征点。正矢图的圆曲段方程为

( 1 )

式中：v为20 m弦的正矢，mm；R为圆曲线半径，m。显然，只要得到圆曲段对应的直线方程，就能求出圆曲线半径R。

角图中，设计线图是“水平线-抛物线-斜直线-抛物线-水平线”的结构，分别对应夹直线、第一缓和曲线、圆曲线、第二缓和曲线、夹直线。其中，第一缓和曲线累积转角为

( 2 )

式中：A(S)为测点的累积转角，rad；S为测点里程，m；ZH为直缓点里程，m；R为圆曲线半径，m；l01为第一缓和曲线的长度，m。

圆曲线累积转角为

( 3 )

式中：HY为缓圆点里程，m。

第二缓和曲线累积转角为

( 4 )

式中：L为圆曲线长度，m；l02为第二缓和曲线长度，m。

本文在拟合角图中的三段直线时使用霍夫加稳健算法；对抛物线段，则在识别出直线点范围后，对剩余的中间两段数据采用稳健估计法识别和拟合。

4 仿真试验

为了提出有效的识别方法，需要用关键参数已知的仿真曲线数据进行试验。首先要构造出仿真曲线的相对测量数据。

4.1 仿真正矢图和角图

在标准设计单曲线的转角数据中加入正态分布的渐变型伪随机偏差得到仿真转角数据，生成对应的仿真正矢图与仿真角图(图3)。两图的偏差均值分别为-0.004 5 mm和0.015 6°，中误差分别为2.659 0 mm和0.094 6°。理论上讲，该仿真曲线的理想曲线应与设计曲线重合，其五大关键参数即为设计值。设计值为：[ZHs,HYs,YHs,HZs,Rs]=[100, 270, 655, 825, 800] (m)，与第2章中提到的实际线路设计值相同。

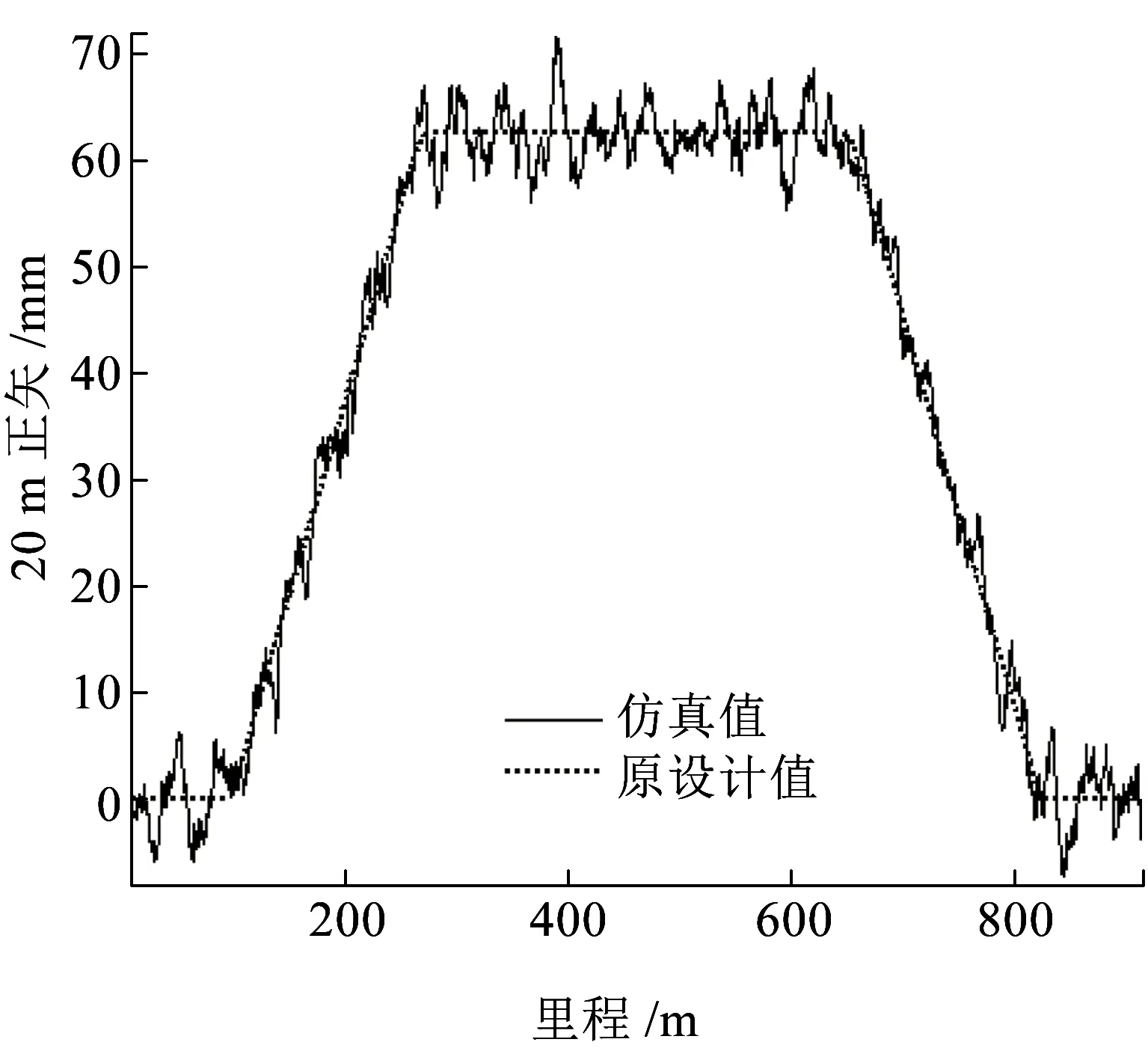
(a)仿真正矢图

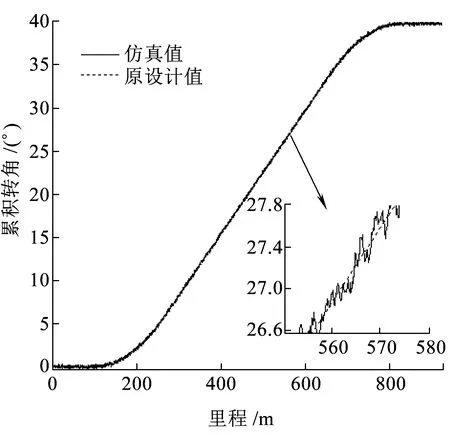
(b)仿真角图图3 仿真线路相对测量数据图

对比图3和图2发现：仿真正矢与角图的波形与实际相似；从统计数据看，仿真正矢与角图偏差的中误差与实际偏差的中误差相近，但均值小一个数量级。上述现象表明，该仿真线路与实际线路相似，但因为其中加入的是期望为0的正态分布随机偏差，其均值偏离零点极小，与实测偏差不同。可以预测，如果识别方法得当，由该仿真数据识别出的关键参数应非常接近设计值，而由实测数据识别出的关键参数则会偏离设计值。

4.2 基于仿真正矢图的识别算法研究

如图4(a)所示，对仿真正矢图先使用霍夫变换识别出四条主线上的数据点，再用稳健估计法拟合成四条直线，求出对应四个特征点的四个交点，交点横坐标即为四大特征点。图4(a)参数识别结果与设计值的偏差见表1。

观察图4(a)发现，各段数据点间仍有交叠。因此可将所识别的四大特征点作为初始特征点，将已识别数据分段，再用稳健估计法拟合四条直线求特征点与半径，此过程不断迭代，直到前后两次迭代得到的特征点差值小于设定阈值为止。识别结果如图4(b)所示，识别结果与设计值的偏差列于表1中。由表1可知，图4(b)的四个特征点比图4(a)更接近设计值，但曲线半径更偏离设计值。

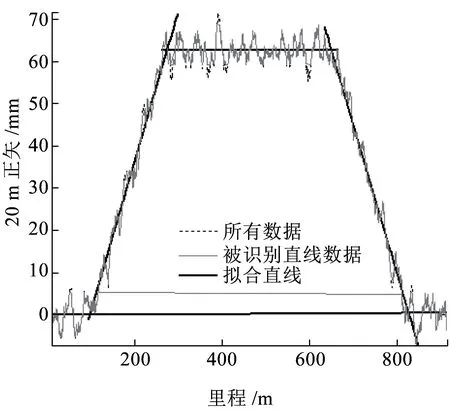
(a)霍夫变换识别加稳健拟合

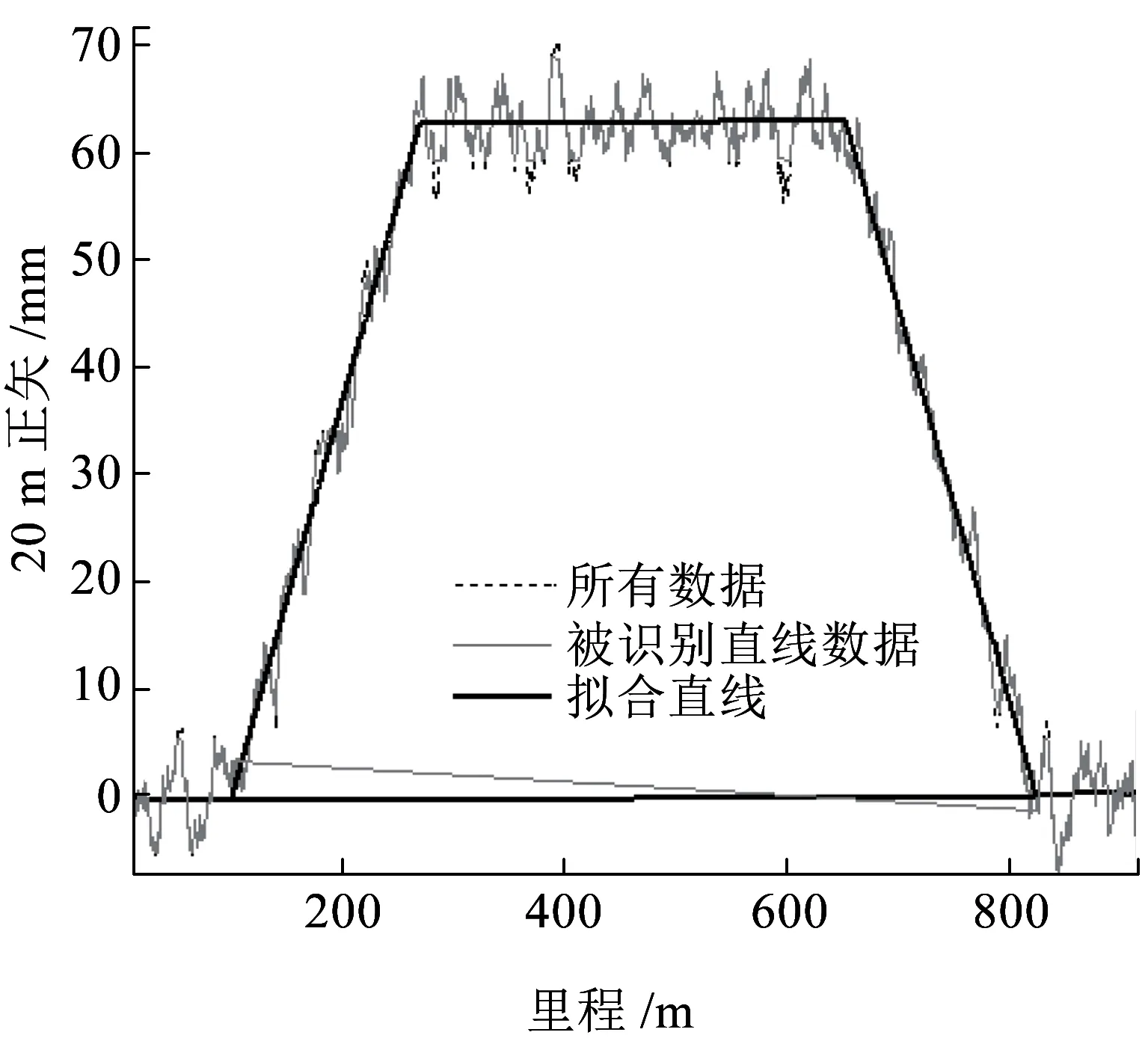
(b)对已识别数据重分段再拟合的迭代结果

(c)对所有数据重分段再拟合的迭代结果图4 基于仿真正矢图的曲线参数识别结果

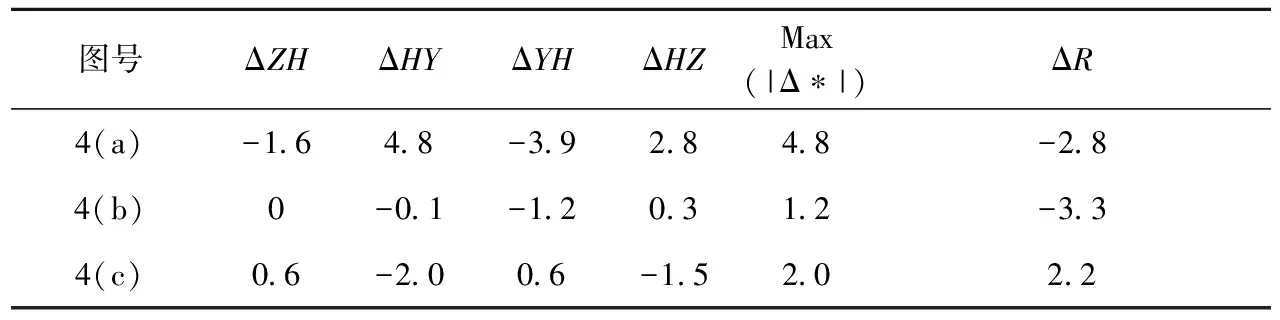
表1 基于仿真正矢图的识别结果偏差 m

注：* 代表特征点。

若将所有数据点用上，按初始特征点将其分段，对各段数据仅使用稳健估计法处理得到拟合直线，再求其交点(即新特征点)和曲线半径。按新特征点将所有数据重新分段，重复上述过程，不断迭代，直到满足迭代终止条件(前后两次特征点差值小于设定阈值)，得到最终特征点和半径。此方法是现在常见的特征点求解方法(稳健估计加迭代算法)，只是在初始特征点的确定上，现有文献主要使用粗略的人工交互式方法[2,14]，而本文直接使用了霍夫加稳健法得到的值，这可以减少迭代次数，但并不影响迭代结果。图4(c)给出了这一常见算法的识别结果，可以看出：仅通过稳健估计排除的异常点较少。由表1数据可知：图4(c)求得的最终特征点比图4(a)的结果有进步，但不及图4(b)的结果；图4(c)求得的曲线半径在三种算法中最接近设计值。

综上所述，以上三种基于正矢图的曲线参数识别算法中，图4(b)算法的特征点识别效果最好，图4(c)算法的曲线半径识别效果最好。

4.3 基于仿真角图的识别算法研究

对仿真角图先用霍夫变换识别出三条直线上的数据，再用稳健估计法拟合成三条直线段；认为直线段范围之外的数据分别是两条抛物线上的数据，对这两段数据用稳健估计法拟合成抛物线。角图中的斜直线对应圆曲段，由式( 3 )知根据斜直线的斜率可求出圆曲线半径；角图中的两条抛物线分别对应第一缓和曲线和第二缓和曲线，由式( 2 )和式( 4 )知，求出曲线半径后，由两抛物线的二次项系数即可求出对应的缓和曲线长l01、l02，而两抛物线的极值点分别对应ZH点和HZ点。该算法的识别结果如图5(a)所示，其与设计值的偏差见表2。将图5(a)与图4(a)的结果比较：图5(a)的识别结果优于图4(a)的结果，尤其是半径，与设计值只差0.5 m；然而，与图4(a)类似的是，图5(a)所识别的特征点与拟合时各段数据的分段点并不一致，例如：识别出的ZH点在101.2 m处，但第一条水平线的拟合数据显然从0直到近150 m处。

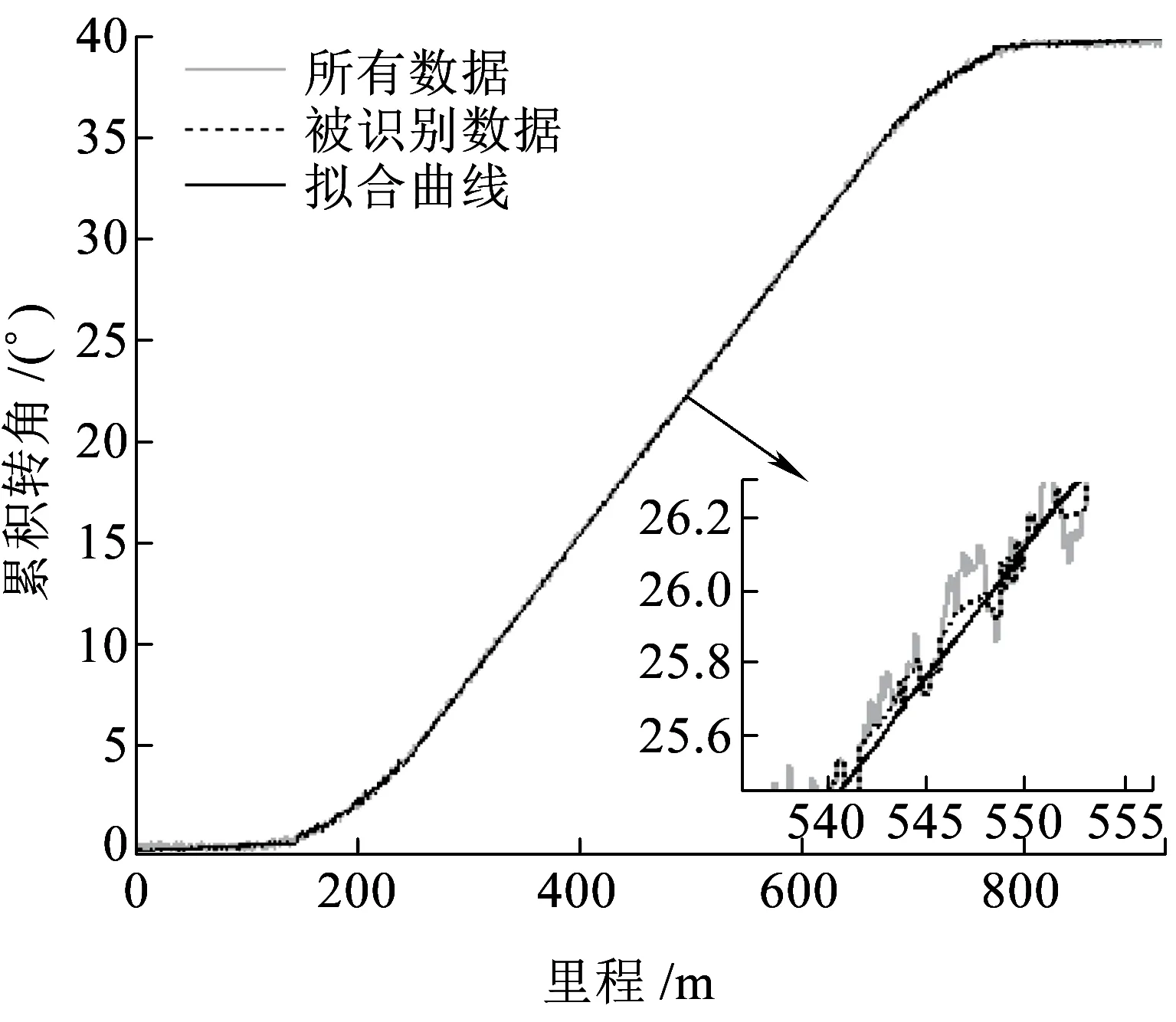
(a)霍夫变换识别加稳健拟合

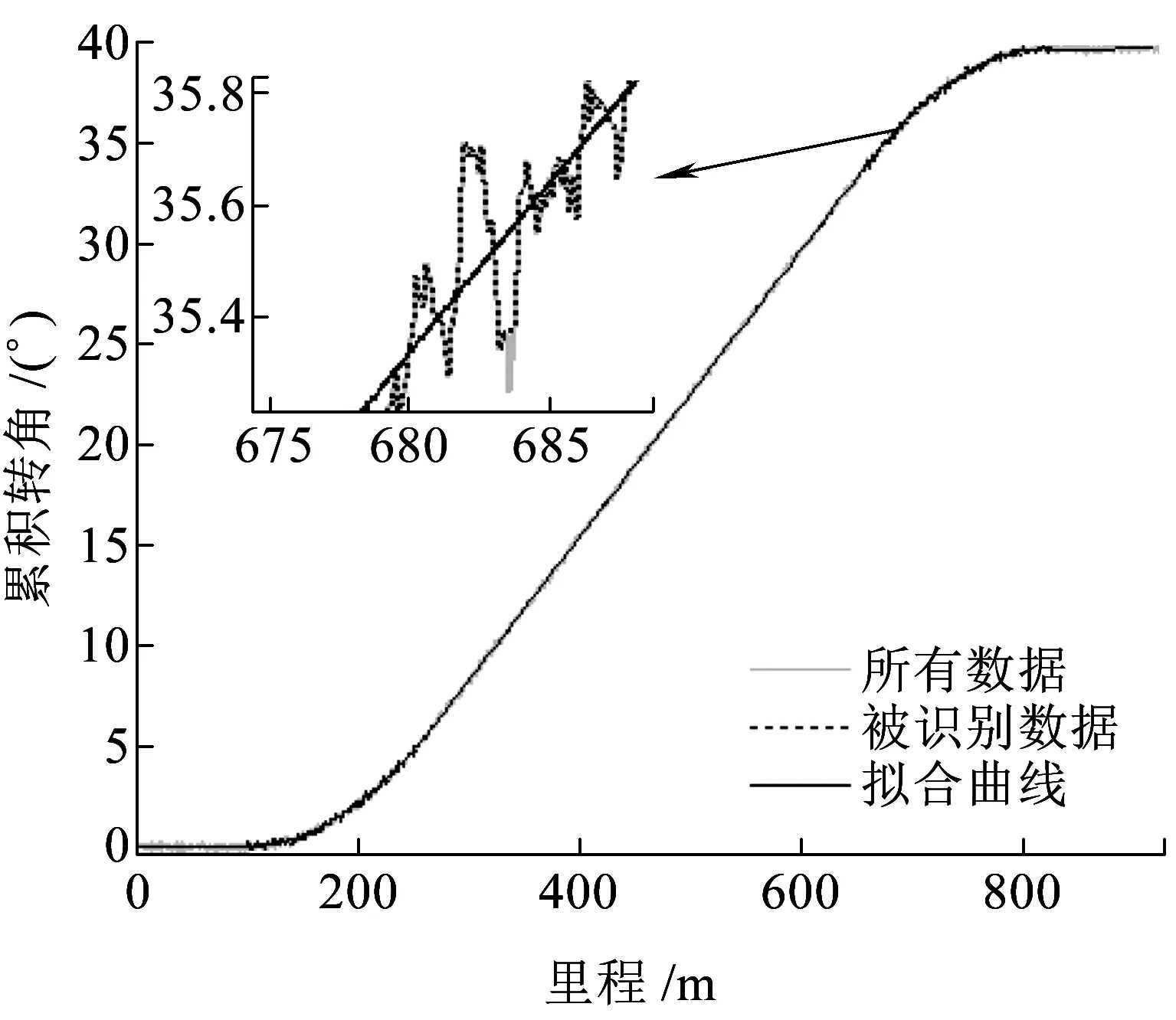
(b)对已识别数据重分段再拟合的迭代结果

根据图5(a) 识别的特征点将数据重新分段，再次用稳健估计法拟合直线与抛物线求得特征点和半径，将此过程不断迭代，直到前后两次迭代得到的四大特征点差值均小于设定阈值。此算法最终识别结果如图5(b)所示。

由表2可知，图5(b)的特征点结果并未优于图5(a)的结果，两者的Max(|Δ*|)均为1.3 m，但若将四大特征点的偏差绝对值相加，图5(a)为3.5 m，图5(b)为4 m，因此总体来看，图5(a)的特征点识别比图5(b)好。但表2的ΔR列显示，图5(b)对曲线半径的识别精度比图5(a)高。

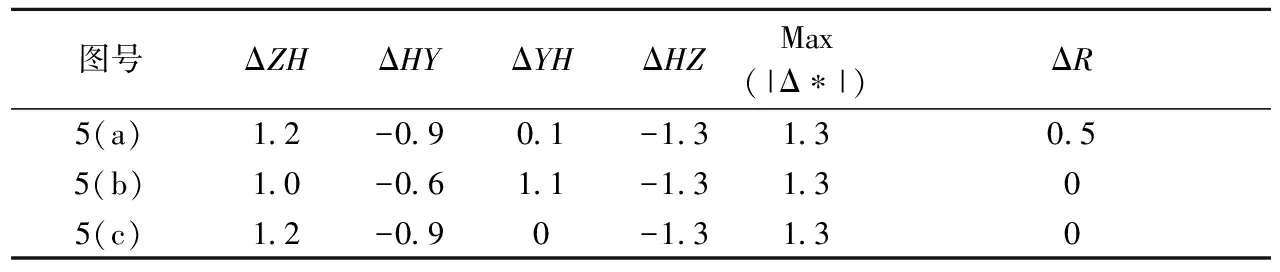
表2 基于仿真角图的识别结果偏差 m

注：* 代表特征点。

鉴于上述原因，拟将算法改为：在按图5(a)的特征点将已识别直线数据重新分段后，只用稳健估计法重新拟合直线，不再修正抛物线方程。运用此方法ZH点与HZ点不变，但得到新的曲线半径。用新半径重算两条缓和曲线长，会得到新的HY点与YH点。此种算法的识别结果如图5(c)所示。由表2易知，图5(c)的识别精度比图5(a)有所提高。

综上，在基于仿真角图的三种识别算法中，图5(c)算法的识别效果最佳。

4.4 新识别算法

4.2节和4.3节研究了六种关键参数识别算法，将这六种算法的识别结果与设计值偏差列于表3中，以便对比和分析。关注Max(|Δ*|)与ΔR列，容易看出：特征点识别最优的是图4(b)的算法，曲线半径识别最优的是图5(b)、图5(c)两算法。

研究表3发现：尽管图4(b)算法的特征点识别总体效果在六种算法中最优，但其识别的 YH点偏差较大，而图5(c)的YH点偏差为0。若能将图4(b)与图5(c)的特征点结果互补，即选择两者中偏差最小的结果作为最终识别结果，可获得更优的识别效果。

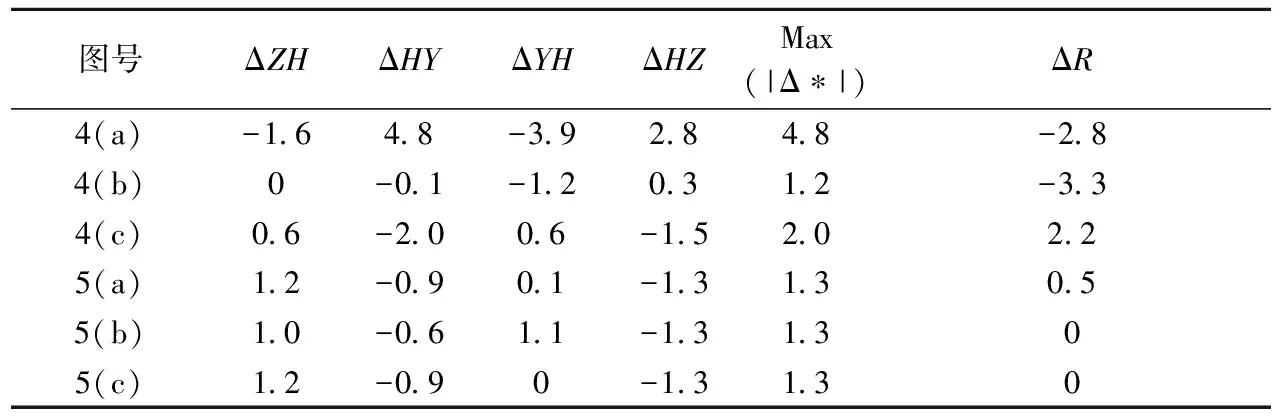
表3 6种算法的仿真曲线参数识别结果偏差 m

注：* 代表特征点。

图4(b)算法是基于正矢图的识别算法，图5(c) 算法是基于角图的识别算法，将两者结果互补后效果会更优的原因可能为：正矢图随机误差较大，抗干扰性弱，但系统误差较小；角图因其累加特性，随机误差小，抗干扰性好，但系统误差会因累加越来越大，因此角图数据和正矢图数据本身具有互补的特点，这就使结果互补能得到更好的识别效果。

将图4(b)和图5(c)的结果互补得到最终识别结果：[ZH，HY，YH，HZ，R]= [100, 269.9, 655, 825.3, 800](m)，其中特征点与设计值最大偏差为0.3 m，曲线半径与设计值一致。

综上所述，提出识别曲线关键参数的新算法：

(1)对正矢图用霍夫加稳健算法拟合直线求交点，得初始特征点；按此初始特征点将已识别数据重新分段进行稳健拟合求交点，得新特征点与曲线半径；将此过程迭代进行，直到前后两次特征点值之差小于设定阈值，得到基于正矢图的曲线参数识别结果。

(2)对角图用霍夫加稳健算法拟合直线后，再用稳健估计法拟合抛物线，根据直线和抛物线方程求曲线半径与初始特征点；按初始特征点将已识别直线数据重分段，再次稳健拟合直线得新曲线半径；使用新曲线半径，根据原拟合抛物线方程得新特征点；此新曲线半径和新特征点即为基于角图的曲线参数识别结果。

(3)将基于正矢图和角图的两种识别结果互补，得出最终的理想曲线关键参数。

5 实例应用

采用新识别算法针对实际线路数据进行曲线关键参数识别，目的是检验该算法的实用性。

如第4章所言，实际曲线的关键参数是未知的，通常也不能与设计值完全吻合。因此，此处仅以“尽量靠近设计值”为准则，用实际数据检验新算法的效果，更重要的一点是检视其是否与应用于仿真数据时的表现一致。

(a)新识别算法中第一步的识别结果

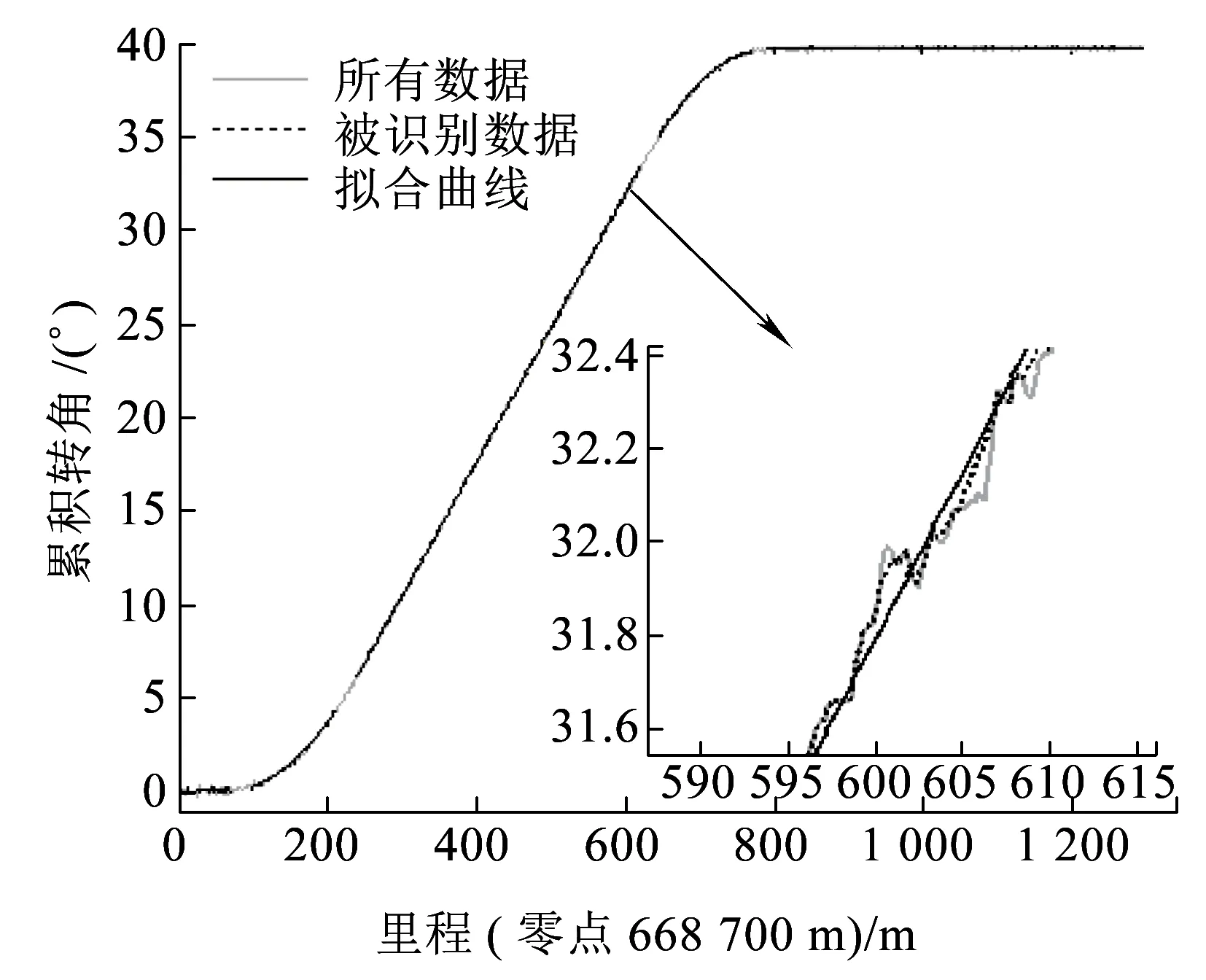
(b)新识别算法中第二步的识别结果图6 基于实测正矢图与角图的曲线参数识别结果

本章所针对的实际线路是图2对应的曲线线路，关键参数设计值为[ZHs,HYs,YHs,HZs,Rs]=[668 768, 668 938, 669 323, 669 493, 800](m)。

由新识别算法第一步得到的识别结果如图6(a)所示，第二步得到的识别结果如图6(b)所示，第三步得到最终识别结果为[ZH,HY,YH,HZ,R]=[668 768.3, 668 940.0, 669 326.6, 669 493.2, 800.0](m)。将这三步的识别结果与设计值的偏差列于表4中。

表4 实际曲线的关键参数识别结果偏差 m

注：* 代表特征点。

仅从表4的Max(|Δ*|)和ΔR列看，基于角图的识别结果明显优于基于正矢图的识别结果。这与算法应用于仿真图时的表现不太一样。仿真结果中，角图图5(c)的特征点识别结果虽与正矢图图4(b)的识别结果有互补之处，但总体上并未优于正矢图结果。

虽然实际与仿真有出入，但出现这一现象的原因容易推测。因为仿真线路的错动是人为安排的正态分布随机变量，而实际线路的错动更随机，且测量时易被噪声干扰。所以在实测数据中，角图较正矢图优越的抗干扰性能突显出来，使得其识别结果在某些正矢数据波动较大的地方明显优于正矢图识别结果。

由正矢图图6(a)可知，在第二缓和曲线段上，正矢数据出现了较大的波动。这应该是导致其识别的YH点和HZ点偏差较大的直接原因。而角图图6(b)的结果在这两点的偏差恰恰较小，直接佐证了正矢图与角图互补这一结论。

由上述可知，新识别算法用于实际线路的结果和用于仿真线路的结果是类似的，基于正矢图的识别结果和基于角图的识别结果具有互补性。

实际数据的特征点识别结果最大偏差为3.6 m，仿真数据的特征点识别结果最大偏差为0.3 m。可见实际线路与设计的一致性不如仿真线路好，这一现象恰恰与本文4.1节中的预测遥相呼应，即“如果识别方法得当，由仿真数据识别出的关键参数应非常接近设计值，而由实测数据识别出的关键参数则会更偏离设计值一些”。实际数据的偏差均值约为仿真数据偏差均值的10倍，其特征点识别结果偏差亦约为仿真结果偏差的10倍，佐证了新识别算法的实用效果。

6 结论

(1)本文以使拟合线上测点数目最大为原则，针对正矢图和角图两种相对测量数据，综合使用霍夫变换、稳健估计和迭代法三种基本算法，对仿真线路的曲线关键参数进行识别与效果分析，提出一种识别理想曲线关键参数的新算法。

(2)仿真试验研究证明：新算法的识别效果优于现行的特征点识别算法(仅基于正矢图的稳健估计加迭代求交点算法)。

(3)新识别算法基于“线形偏离设计位置是微小量”这一认识，考虑到正矢图与角图互补这一特征，将正矢图与角图的识别结果结合，以优化最终识别结果。

(4)实际线路数据佐证了新算法的实用性。

参考文献：

[1]EASA S M. Practical Optimization Model for Realigning Railway Horizontal Curves[J]. Civil Engineering Systems，1991，8(1)：27-36.

[2]张安静. 铁路曲线的刚性拟合和柔性拟合[J]. 铁道学报，1986，8(2)：60-73.

ZHANG Anjing. Rigid and Flexible Fitting of Railway Curves[J]. Journal of the China Railway Society，1986，8(2)：60-73.

[3]丁克良，刘大杰，周全基. 既有铁路曲线整正平差算法[J]. 测绘学报，2004，33(3)：195-199.

DING Keliang，LIU Dajie，ZHOU Quanji. Adjustment Algorithm for Realignment of the Existing Railway Curve [J]. Acta Geodaetica et Cartographica Sinica，2004，33(3)：195-199.

[4]秦方方，易思蓉，杨长根. 基于三次样条曲线的铁路既有曲线整正方法[J]. 中国铁道科学，2010，31(2)：18-23.

QIN Fangfang，YI Sirong，YANG Changgen. Method for the Realignment of the Existing Railway Curve Based on the Cubic Spline Curve [J]. China Railway Science，2010，31(2)：18-23.

[5]李红艳，陈治亚，邢诚，等. 铁路既有线曲线复测计算方法[J]. 中国铁道科学，2009，30(2)：18-22.

LI Hongyan，CHEN Zhiya，XING Cheng，et al. Calculation Method for Curve Re-surveying of the Existing Railway Line[J]. China Railway Science，2009，30(2)：18-22.

[6]彭欣. 既有线平面线形参数优化估计研究及CAD系统开发[D]. 长沙：中南大学，2014.

[7]何曲波. 曲线拨道量的优化计算[J]. 铁道建筑，1997(3)：33-36.

[8]刘冬初，解传银. 用最小二乘法选择既有曲线最佳半径[J]. 铁道学报，1987,9(3)：85-89.

[9]缪鹍，田家凯，杨小礼. 基于PSO的既有线曲线整正方法[J]. 中国铁道科学，2014，35(3)：8-14.

MIAO Kun，TIAN Jiakai，YANG Xiaoli. Realignment Method for Existing Railway Curve Based on PSO[J]. China Railway Science，2014，35(3)：8-14.

[10]宋韬. 铁路既有线整正优化相关算法研究[D]. 成都：西南交通大学，2014.

[11]陈峰. 提速线路精密测量、重构与优化整正研究[D]. 长沙：中南大学，2013.

[12]TONG X H，MENG X L，DING K L. Estimating Geometric Parameters of Highways and Railways Using Least-squares Adjustment[J]. Empire Survey Review，2010，318(42)：359-374.

[13]DWYER D O. Realignment of Railway Curves[J]. Transport，1997，123(4)：234-240.

[14]姚连璧，刘春. 样条函数与稳健估计在线路线形识别中的应用[J]. 同济大学学报:自然科学版，2004，32(7)：943-946.

YAO Lianbi，LIU Chun. Spline Function and Robust Estimation Applied in Line Type Identification for Railways [J]. Journal of Tongji University: Natural Science，2004，32(7)：943-946.

[15]俞佳伟. 基于轨检车数据的铁路曲线整正计算方法研究[D]. 成都：西南交通大学，2014.

[16]魏晖，朱洪涛，万坚. 绝对测量在无砟轨道的轨向控制中的精度分析[J]. 铁道工程学报，2012(5)：1-5.

WEI Hui，ZHU Hongtao，WAN Jian. Analysis of Accuracy of Absolute Survey in Control of Horizontal Regularity of Ballastless Track [J]. Journal of Railway Engineering Society，2012(5)：1-5.

[17]曾接贤，张桂梅，储珺，等. 霍夫变换与最小二乘法相结合的直线拟合[J]. 南昌航空工业学院学报：自然科学版，2003，17(4)：9-13.

ZENG Jiexian，ZHANG Guimei，CHU Jun，et al. Fit Line Using a Method Combined Hough Transform with Least Square[J]. Journal of Nanchang Institute of Aeronautical Technology： Natural Science，2003，17(4)：9-13.